Pola wielokątów
3. Pole trójkąta

W tablicach matematycznych znajduje się zazwyczaj siedem różnych wzorów na obliczenie pola trójkąta. Jeden z nich nazywa się wzorem Herona, od imienia greckiego matematyka, fizyka i wynalazcy urządzeń.
W tym materiale zawarte są informacje na temat obliczania pól i obwodów trójkątów. Zamieszczone tu przykłady pokazują w jaki sposób wyznaczamy pola i obwody różnych trójkątów.
Pole trójkąta jest równe połowie iloczynu długości jego podstawy oraz wysokości prostopadłej do tej podstawy.

Podstawą trójkąta nazywamy ten bok trójkąta, do którego poprowadzona jest wysokość.
Zapoznaj się z poniższą animacją, która pokazuje dwa sposoby wyznaczenia wzoru na pole trójkąta.

Film dostępny pod adresem /preview/resource/R13naivt2OXEQ
Animacja przedstawia dwa różne sposoby wyznaczania wzoru na pole trójkąta.
Obliczmy pole trójkąta, który jest fragmentem fasady budynku.

Pole trójkąta wynosi .
Widok z przodu karmnika ma kształt trójkąta. Jakie jest pole tego trójkąta?

Pole trójkąta wynosi .
Pole trójkąta prostokątnego o przyprostokątnych długości i jest równe połowie pola prostokąta o wymiarach i .

Pole trójkąta prostokątnego jest równe połowie iloczynu długości jego przyprostokątnych.

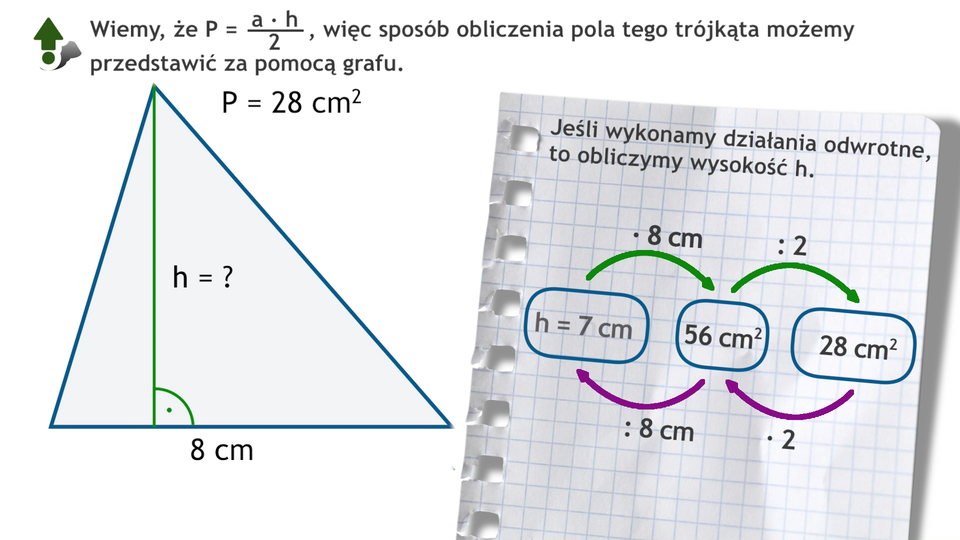
Film dostępny pod adresem /preview/resource/RPsbluvhqurcr
Animacja przedstawia, w jaki sposób obliczyć wysokość trójkąta mając daną długość boku trójkąta, na który opada ta wysokość oraz pole trójkąta.
Zapoznaj się z poniższym apletem i wykonaj polecenia.
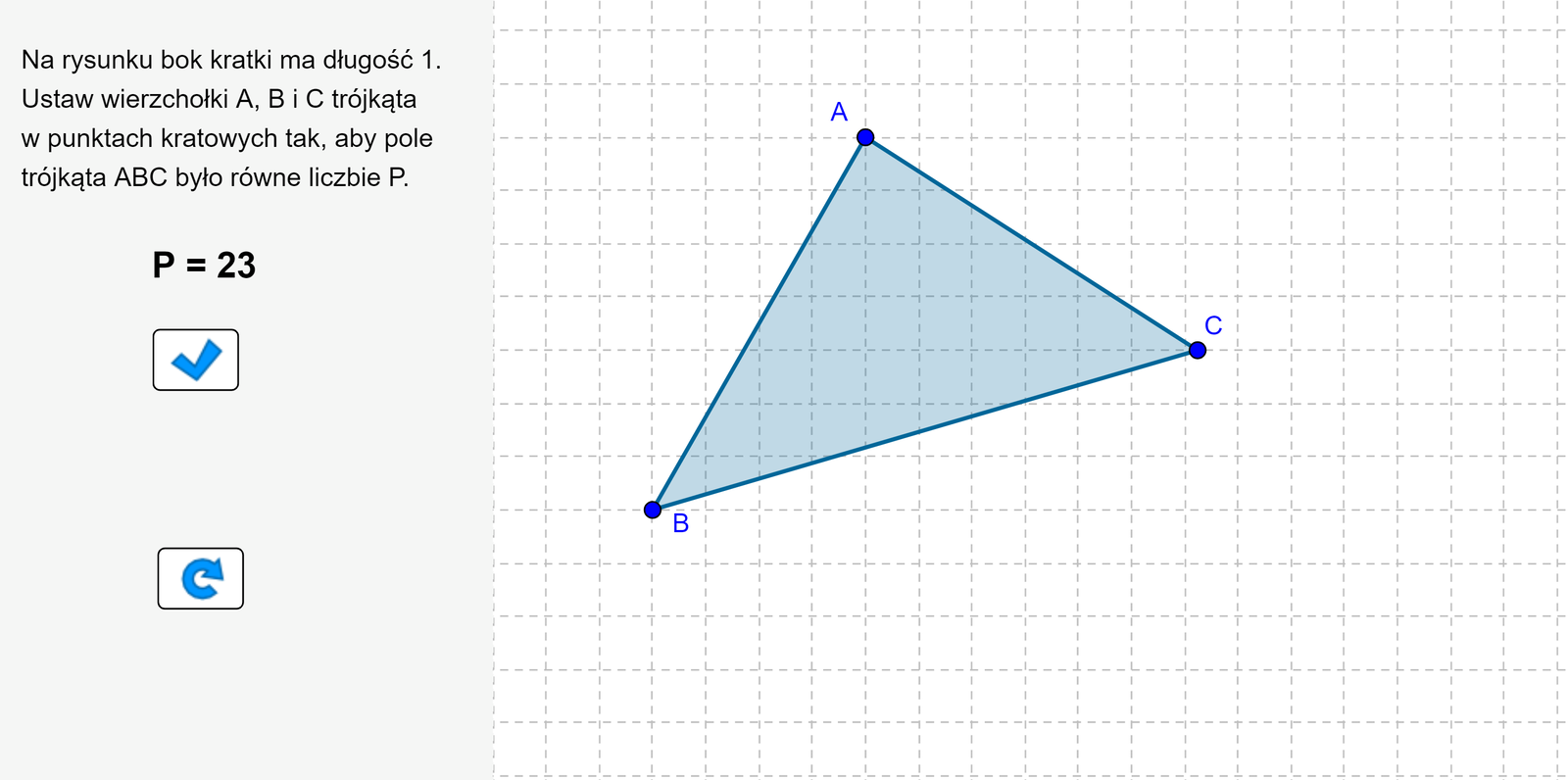
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DVfKhimvM
Wysokość ma długość , a długości boków , i wynoszą odpowiednio , i .

Długości boków trójkątów widocznych na rysunku są następujące
,
,
,
,
.

Obwód trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
Wykorzystaj dane z rysunku i oblicz obwód trójkąta .

Obwód trójkąta wynosi , a trójkąta wynosi . Odcinek ma długości. Oblicz obwód czworokąta .

Z dwóch trójkątów równobocznych o obwodzie każdy, odcięto po trzy trójkąty równoboczne o boku . Powstała figura oraz figura widoczne na poniższym rysunku.

Przyjrzyj się trójkątom na rysunku.
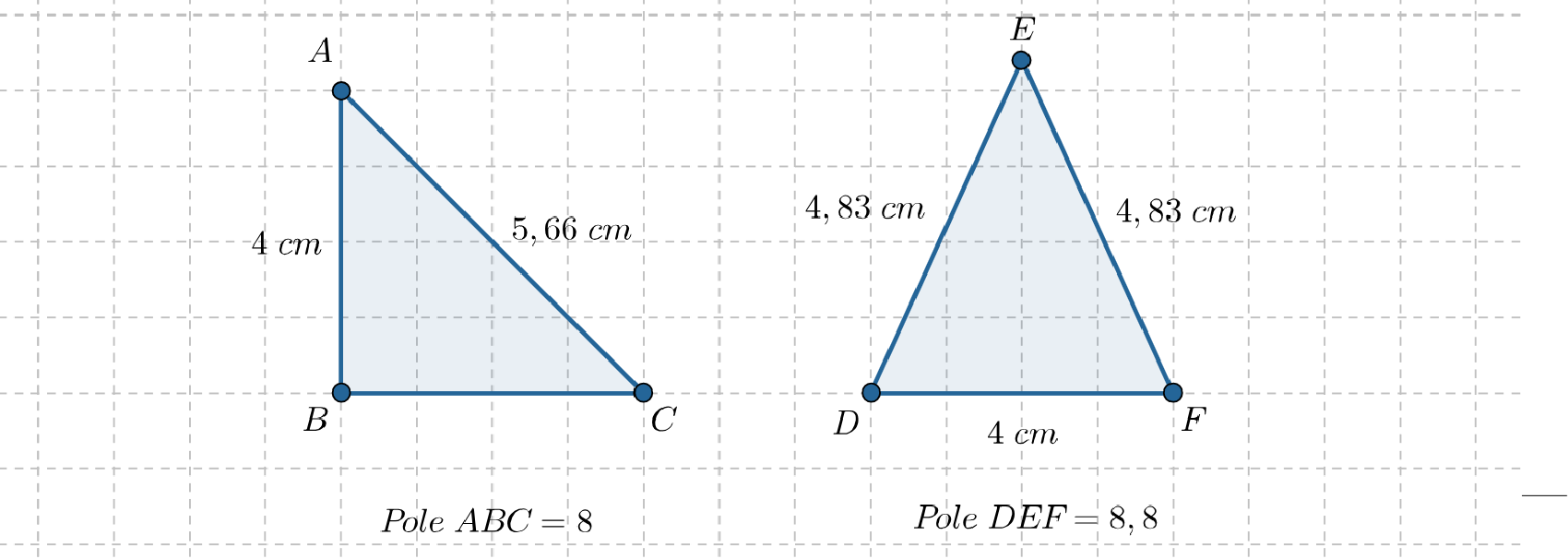
Odpowiedź: Trójkąty te mają jednakowe 1. obwody, 2. , 3. pola, 4. boki, 5. , 6. wysokości, 7. , 8. .
Jaka jest długość wysokości trójkąta opuszczonej na bok ?
Odpowiedź: Wysokość trójkąta wynosi 1. obwody, 2. , 3. pola, 4. boki, 5. , 6. wysokości, 7. , 8. .
- Wszystkie trójkąty o jednakowym obwodzie mają równe pola.
- Trójkąt prostokątny o przyprostokątnych długości i ma obwód równy .
- Trójkąt równoramienny o podstawie i ramieniu ma obwód równy .
- Trójkąt równoramienny o podstawie i ramieniu ma pole równe .
- Nie ma trójkąta równoramiennego o podstawie i ramieniu .
Długości boków trójkąta oznaczono literami , i . Litery , i oznaczają długości wysokości tego trójkąta poprowadzone odpowiednio do boków , i .

Zapoznaj się z poniższym rysunkiem, na którym przedstawione są cztery trójkąty.

Wykonaj potrzebne obliczenia i uzupełnij zdania, wpisując w luki odpowiednie liczby. Pole tego trójkąta wynosi Tu uzupełnij.Wysokość prostopadła do ramienia trójkąta ma długość Tu uzupełnij.
Na bokach trójkąta prostokątnego zbudowano trójkąty prostokątne równoramienne, tak jak na poniższym rysunku.

Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.