Graficzna ilustracja zależności między wielkościami fizycznymi, które wpływają na przebieg zjawiska fizycznego, pozwala na uproszczenie jego opisu, ułatwia ich odczyt i obliczenie szukanych wartości. Korzystaj z wykresów, kiedy to tylko możliwe!

RI8xhIt1ZCBzA1

Zdjęcie przedstawia skoczka narciarskiego w powietrzu tuż po wyjściu z progu. Jest on zwrócony w lewą stronę kadru, a ciało układa się już w sylwetkę odpowiednią do układu V. Tło jest białe, kombinezon sportowca i jego narty są czarno żółte. — Jedyną siłą napędową skoczka podczas najazdu jest siła grawitacji, ale wystarczy ona, by nadać mu przyspieszenie. By dokładniej opisać ten ruch, trzeba się posłużyć odpowiednim wykresem

Już potrafisz

podawać definicję ruchu jako zmianę położenia względem wybranego układu odniesienia;
klasyfikować ruchy ze względu na tor (prostoliniowe i krzywoliniowe) oraz wartość prędkości (jednostajne i zmienne);
odróżniać prędkość średnią od chwilowej;
obliczać prędkość i wyrażać ją w różnych jednostkach;
podawać definicje przyspieszenia oraz ruchu przyspieszonego i opóźnionego;
obliczać przyspieszenie, gdy prędkość rośnie lub maleje;
obliczać zmiany prędkości podczas ruchu jednostajnie przyspieszonego.

Nauczysz się

obliczać drogę przebytą przez ciało w ruchu jednostajnie przyspieszonym prostoliniowym;
sporządzać wykresy zależności drogi od czasu, przyspieszenia od czasu i prędkości od czasu dla ciał poruszających się ruchem jednostajnie przyspieszonym prostoliniowym;
odczytywać wykresy i obliczać na ich podstawie wartości drogi, przyspieszenia i prędkości.

iMT8Y5NXq8_d5e183

1. Zależność przyspieszenia od czasu

W ruchu jednostajnie przyspieszonym prostoliniowym wartość przyspieszenia jest stała.

* W ruchu jednostajnie przyspieszonym prostoliniowym wektor przyspieszenia jest stałyiMT8Y5NXq8_d435e112jest stały.

R1E8yCPm3m0L41

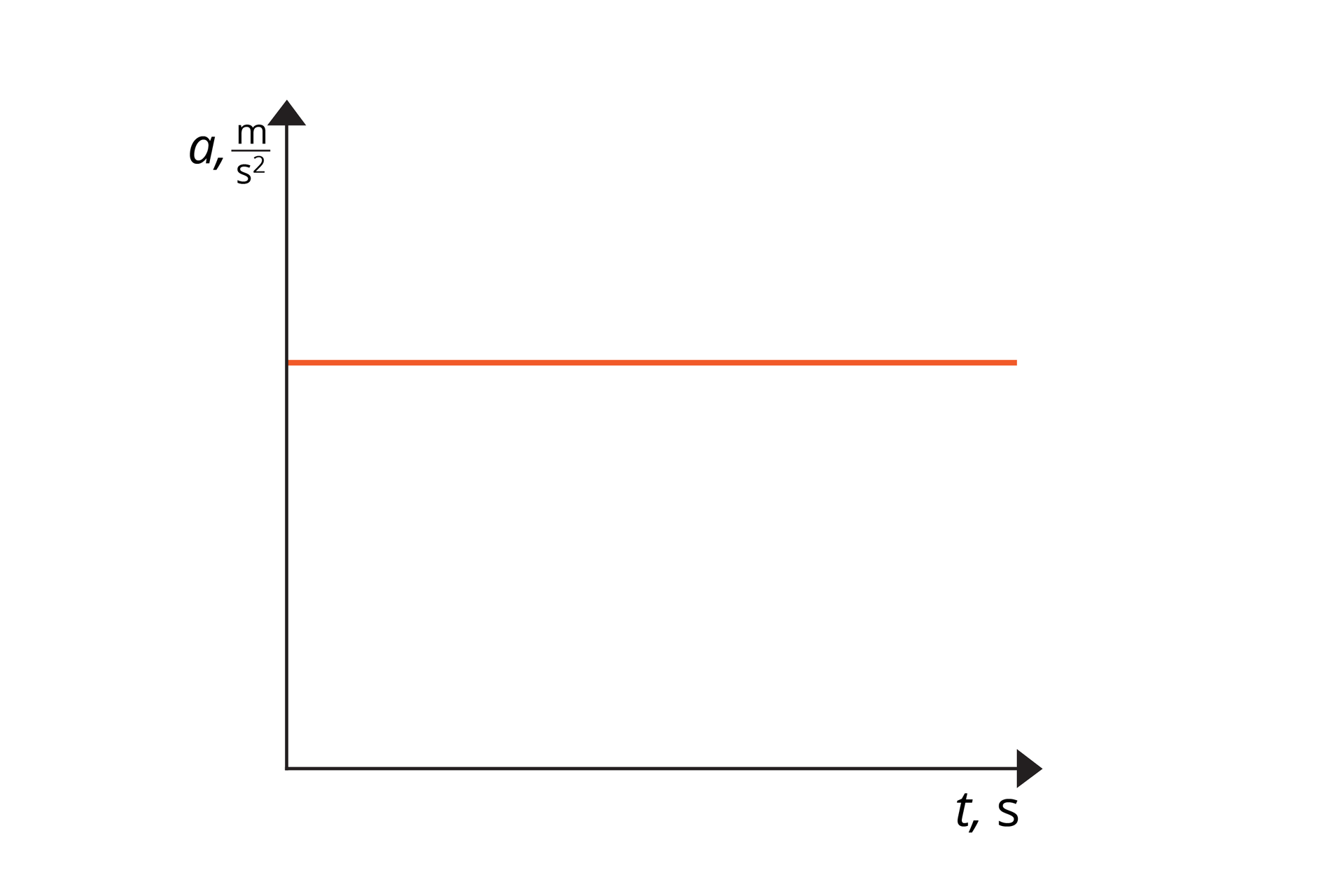
Schemat przedstawia wykres zależności przyspieszenia od czasu. Oś odciętych opisana jako „t,s”. Oś rzędnych opisana jako „a, m/s do kwadratu”. Na wykresie widoczny pomarańczowy odcinek. Odcinek równoległy do osi odciętych. Początek na osi rzędnych, nieco powyżej połowy jej długości. — Wykres zależności przyspieszenia od czasu dla ruchu jednostajnie przyspieszonego prostoliniowego

Zapamiętaj!

Wykresem zależności przyspieszenia od czasu jest linia prosta równoległa do osi czasu. Obrazuje ona to, że w ruchu jednostajnie przyspieszonym prostoliniowym przyspieszenie jest stałe.

iMT8Y5NXq8_d435e112

iMT8Y5NXq8_d5e262

2. Zależność prędkości od czasu

Ruch jednostajnie przyspieszony prostoliniowy odbywa się ze stałym przyspieszeniem.

Oznacza to, że w równych ostępach czasu obserwujemy określony, zawsze jednakowy przyrost prędkości poruszającego się ciała. Prędkość końcową obliczamy za pomocą wzoru:

v_{k} = v_{0} + a \cdot t

gdzie: $v_{k} -$ prędkość końcowa; $v_{0} -$ prędkość początkowa; $a -$ przyspieszenie; $t -$ czas. Zależność v(t) ruchu możemy przedstawić graficznie. Poniżej przedstawiono te zależności dla $v_{0} = 0.$ Dla wartości prędkości początkowej różnej od zera wykresy można skonstruować przy użyciu znajdującej się niżej aplikacji.

R8en2Pr7u7uGe1

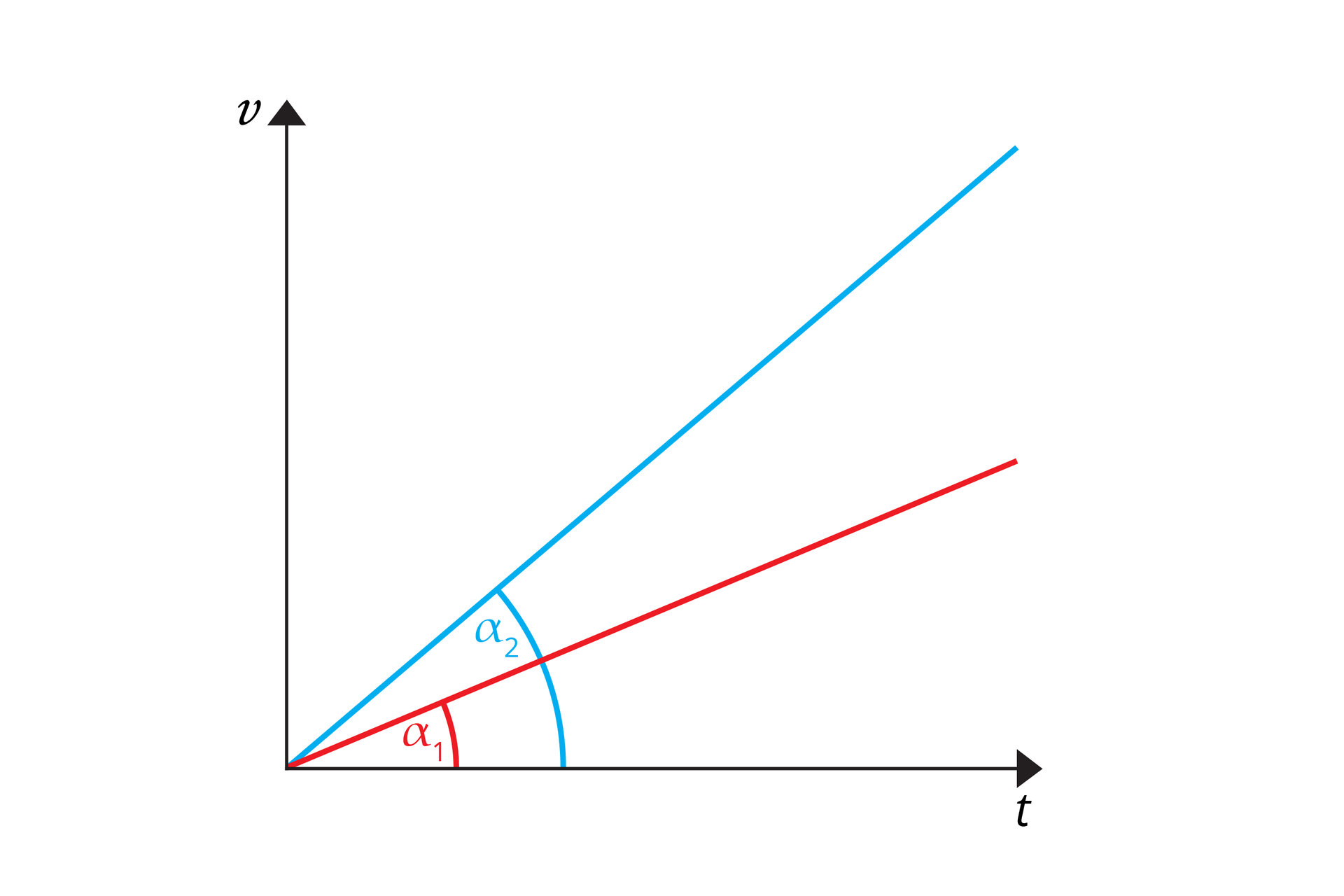
Schemat przedstawia wykres zależności prędkości od czasu. Oś odciętych opisana jako „t,”. Oś rzędnych opisana jako v”. Na wykresie widoczne dwa odcinki: niebieski i czerwony. Oba mają początek w początku układu współrzędnych. Odcinek niebieski leży względem osi odciętych pod kątem ok. 45 stopni. Odcinek czerwony leży względem osi odciętych pod ostrzejszym kątem. Na wykresie greckimi literami oznaczono kąty. Dla odcinka czerwonego α1. Dla odcinka niebieskiego α2. — W ruchu prostoliniowym ze stałym przyspieszeniem wartość prędkości ciała rośnie liniowo

Im większa jest wartość przyspieszenia (szybszy przyrost prędkości), tym kąt nachylenia wykresu do osi czasu jest większy.

Jeśli ciało rozpoczyna ruch ze stanu spoczynku, to prędkość początkowa tego ciała wynosi $0 \frac{m}{s}$ .

R1FRllmDUe33X1

Schemat przedstawia wykres zależności prędkości od czasu. Oś odciętych opisana jako „t,s”. Oś rzędnych opisana jako „v, m/s”. Na wykresie widoczny czerwony odcinek. Początek w początku układu współrzędnych. Odcinek leży względem osi odciętych pod kątem ok. 45 stopni. — Wykres zależności wartości prędkości poruszającego się ciała *v(t)* dla prędkości początkowej $v_{0} = 0 \frac{m}{s}$

Polecenie 1

Za pomocą aplikacji odczytaj wartości prędkości ciał w ruchu jednostajnym prostoliniowym, jeśli:

$a = 1 \frac{m}{s^{2}}$ , $v_{0} = 5 \frac{m}{s}$ w 1., 5. i 10. s ruchu;
$a = 1 \frac{m}{s^{2}}$ , $v_{0} = 0 \frac{m}{s}$ w 1., 5. i 10. s ruchu;
$a = 10 \frac{m}{s^{2}}$ , $v_{0} = 2 \frac{m}{s}$ w 3., 4. i 5. s ruchu;
$a = 10 \frac{m}{s^{2}}$ , $v_{0} = 0 \frac{m}{s}$ w 3., 4. i 5. s ruchu;
$a = 5 \frac{m}{s^{2}}$ , $v_{0} = 1 \frac{m}{s}$ w 3., 5. i 7. s ruchu;
$a = 5 \frac{m}{s^{2}}$ , $v_{0} = 0 \frac{m}{s}$ w 3., 5. i 7. s ruchu.

RkqMNljAgvawj1

Konstruktor wykresów *v(t)* dla ruchu jednostajnie przyspieszonego

Polecenie 2

Narysuj w zeszycie wykres zależności prędkości od czasu dla ruchu jednostajnie przyspieszonego prostoliniowego. Przyjmij, że prędkość początkowa vIndeks dolny 0 = 1 m/s. Rozważ kilka wybranych wartości przyspieszenia.

iMT8Y5NXq8_d5e378

3. Droga w ruchu jednostajnie przyspieszonym

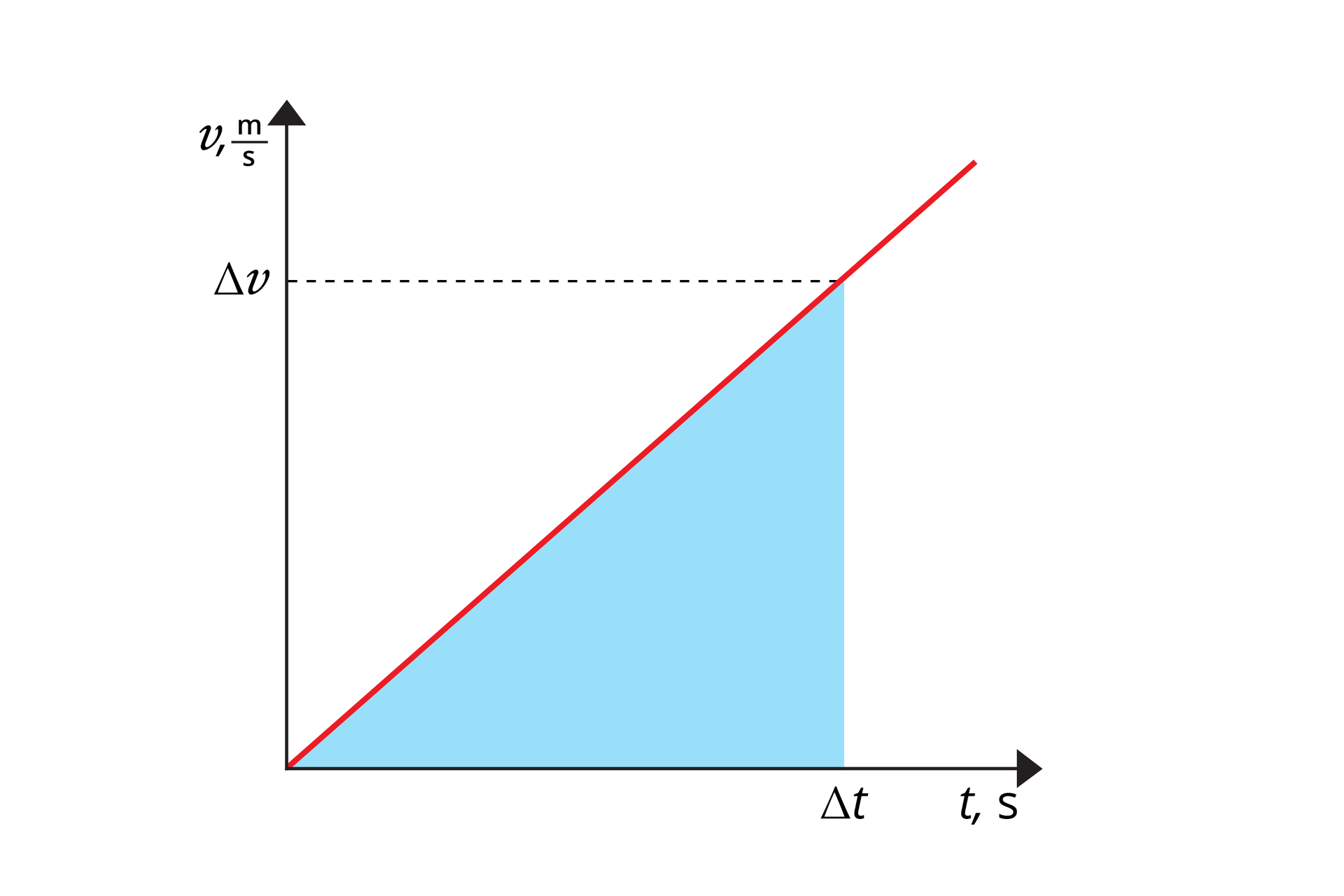
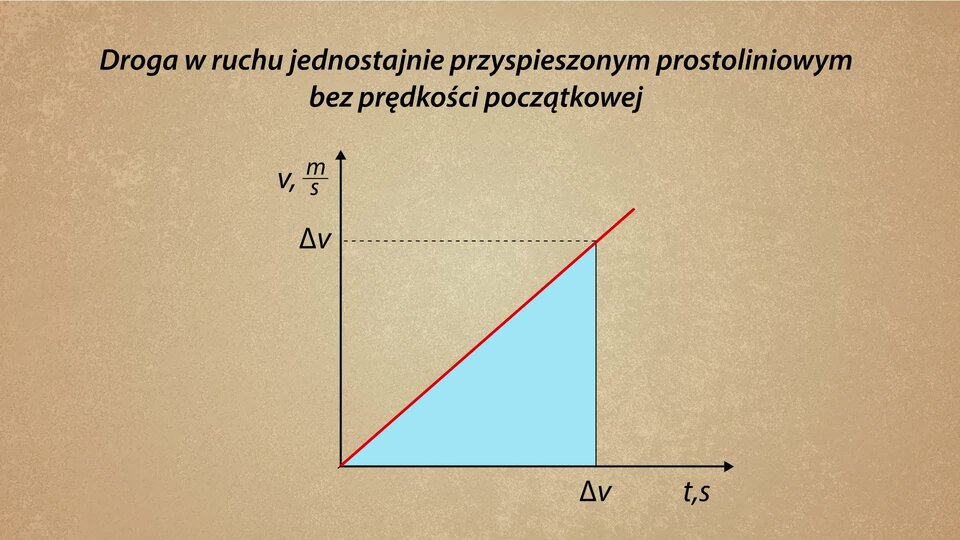
Jeśli znamy pole powierzchni figury znajdującej się pod wykresem zależności v(t), możemy obliczyć drogę, którą przebyło ciało w pewnym przedziale czasowym.

Gdy ciało rozpoczęło ruch ze stanu spoczynku ( $v_{0} = 0 \frac{m}{s}$ ), to obszar pod wykresem odpowiada polu powierzchni trójkąta.

R1V7tCJ6sYDjd1

Droga w ruchu jednostajnym przyspieszonym bez prędkości początkowej

Na poniższej animacji zobaczysz, jak wyznaczać drogę w ruchu jednostajnie przyspieszonym prostoliniowym.

RQ6eB68srdlHD1

Jak obliczyć drogę w ruchu jednostajnie przyspieszonym?

Zapamiętaj!

Jeśli ciało poruszające się ruchem jednostajnie przyspieszonym prostoliniowym rozpoczynało ruch ze stanu spoczynku ( $v_{0} = 0 \frac{m}{s}$ ), drogę oblicza się za pomocą wzoru:
$s = \frac{1}{2} \cdot a \cdot t^{2}$
gdzie: $s [m]$ – droga; $a [\frac{m}{s^{2}}]$ – przyspieszenie; $t [s]$ – czas ruchu ciała.

Polecenie 3

Jaką drogę przebędzie ciało w ciągu 8 sekund, jeśli jego prędkość początkowa była równa zeru, a przyspieszenie wyniosło $3 \frac{m}{s^{2}}$ ? Dokonaj obliczeń, a wynik potwierdź za pomocą aplikacji.

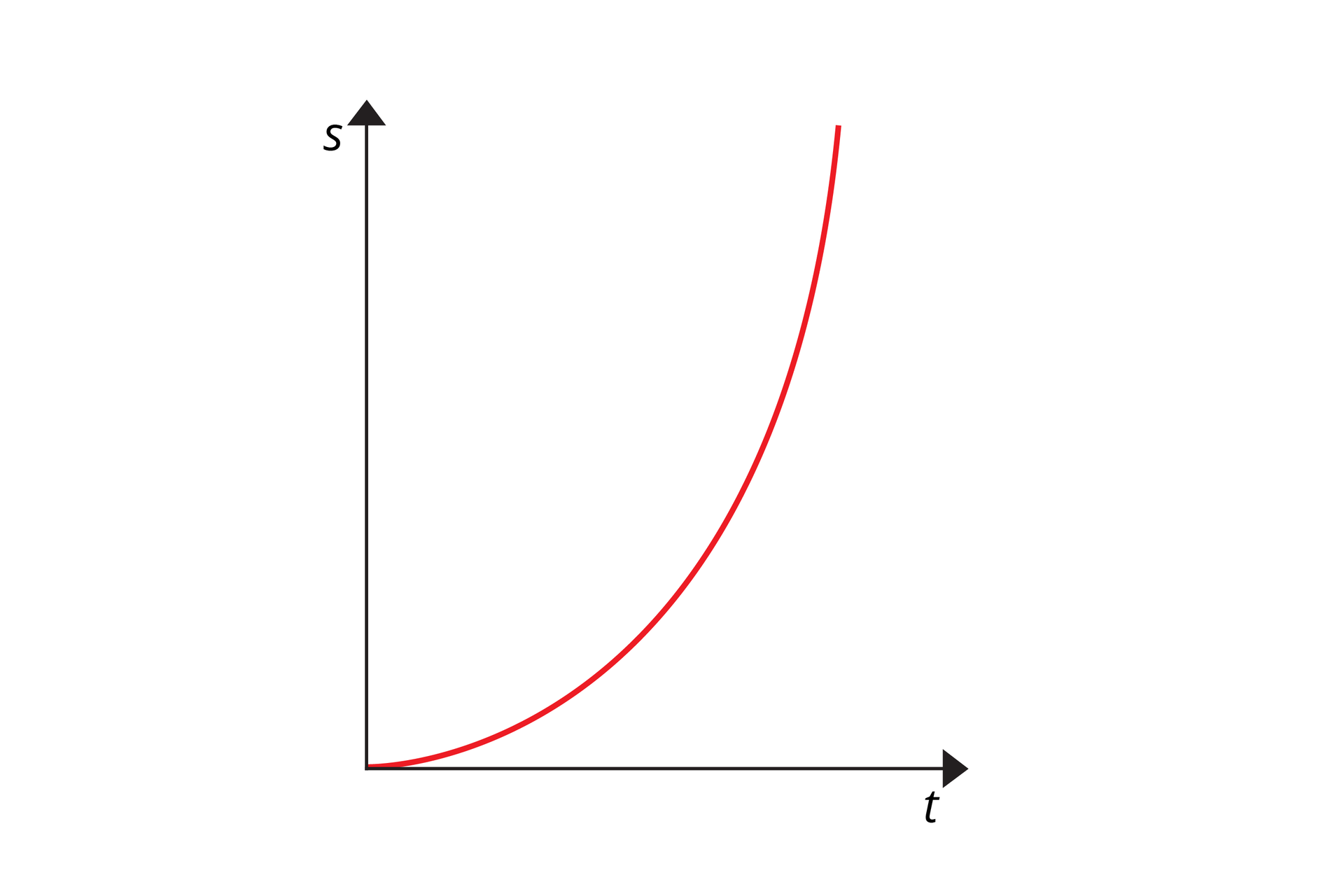
W ruchu jednostajnym prostoliniowym wykres zależności drogi od czasu jest linią prostą nachyloną pod pewnym kątem do osi czasu. Czy tak samo jest w ruchu jednostajnie przyspieszonym?

W ruchu jednostajnym prostoliniowym ciało w równych odstępach czasu ciało pokonuje takie same odcinki drogi $-$ prędkość jego stała. Natomiast w ruchu jednostajnie przyspieszonym prędkość ciała w tych samych przedziałach czasu rośnie, a więc musi wzrastać także długość kolejnych odcinków drogi pokonywanej przez to ciało. Wykres zależności drogi od czasu w ruchu jednostajnie przyspieszonym prostoliniowym bez prędkości początkowej nie jest już linią prostą. Krzywa, która tworzy ten wykres, to część paraboli, tj. wykresu funkcji kwadratowej y = a · xIndeks górny 2.

R1HBZOah2ukBr1

Schemat przedstawia wykres zależności drogi od czasu. Tło białe. Oś odciętych opisana jako „t”. Oś rzędnych opisana jako „s”. Na wykresie znajduje się czerwona linia. Początek w początku układu współrzędnych. Linia przyjęła kształt połowy paraboli z ramionami skierowanymi do góry. Najniższy punkt paraboli przypada na początek układu współrzędnych. — Droga w ruchu jednostajnie przyspieszonym jest kwadratową funkcją czasu

Skonstruujmy wykres zależności s(t) dla ruchu jednostajnie przyspieszonego prostoliniowego.

R1GBsuHnRalN31

Jak zbudować wykres zależności drogi od czasu w ruchu jednostajnie przyspieszonym?

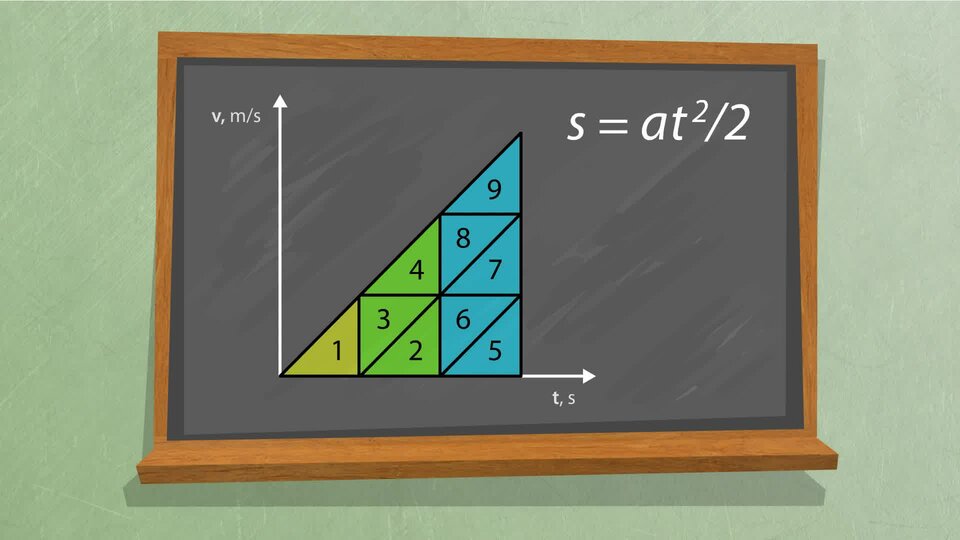
Animacja wykazała również, że obliczone długości odcinków pokonywanych w kolejnych sekundach mają się do siebie tak, jak następujące po sobie liczby nieparzyste.

Polecenie 4

Wykonaj pomiary ponownie, ale wybierz różne kąty. Otrzymane wyniki porównaj z wielkościami otrzymanymi w pierwszym doświadczeniu.

Ciekawostka

R1UhqmlrUrZNc1

Zapamiętaj!

W ruchu jednostajnie przyspieszonym prostoliniowym przyrosty przebytej drogi w kolejnych sekundach ruchu mają się do siebie tak, jak następujące po sobie liczby nieparzyste.

iMT8Y5NXq8_d5e531

Podsumowanie

Wykresem zależności przyspieszenia od czasu jest linia prosta równoległa do osi czasu. Jest tak, ponieważ w ruchu jednostajnie przyspieszonym prostoliniowym wartość przyspieszenia jest stała.
R1E8yCPm3m0L41
Wykres zależności przyspieszenia od czasu dla ruchu jednostajnie przyspieszonego prostoliniowego

Pole powierzchni zawarte pod wykresem zależności prędkości od czasu w ruchu jednostajnie przyspieszonym prostoliniowym jest równe drodze, którą przebyło ciało w określonym czasie.
R16WkmWfDsXlV1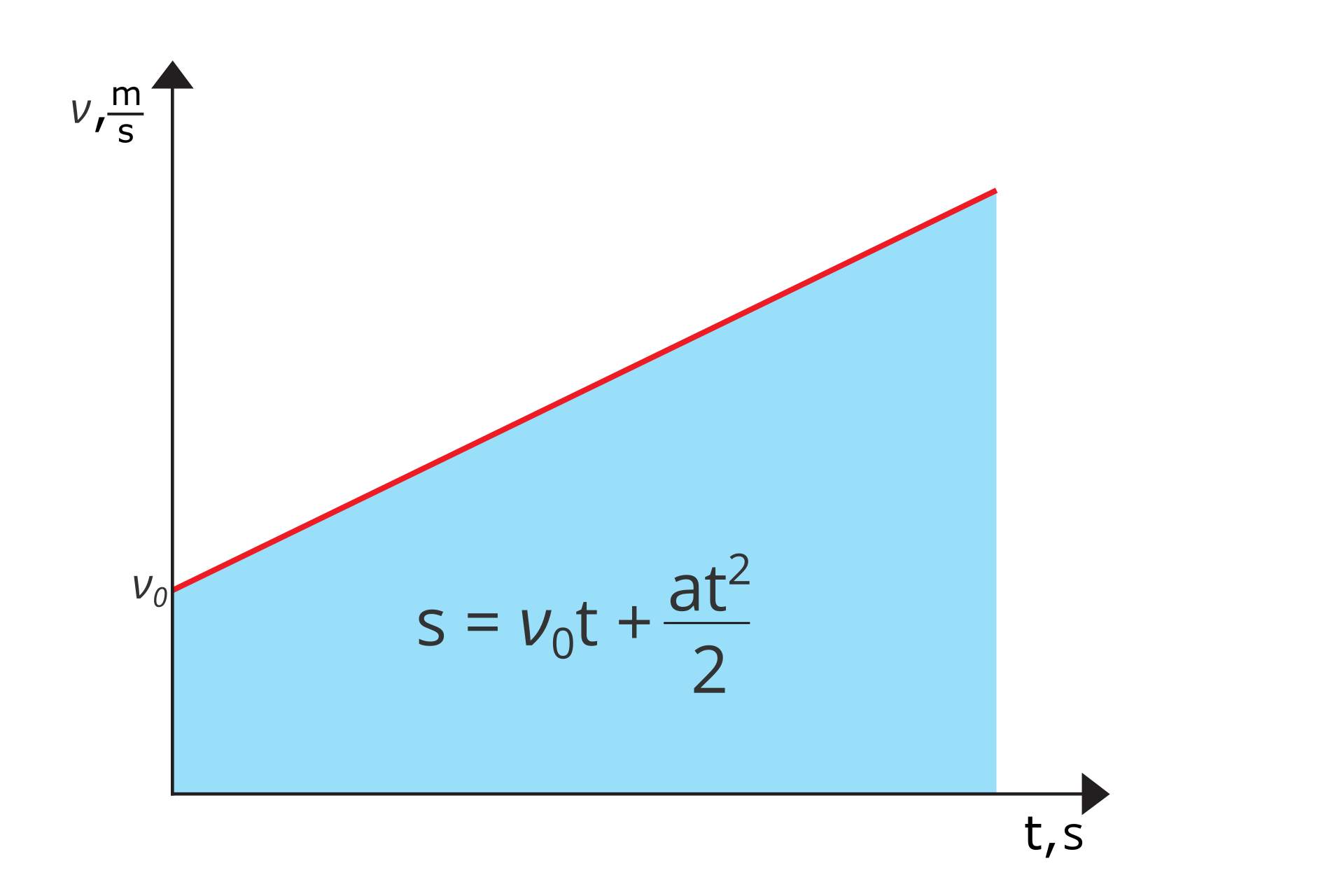
Znajomość pola powierzchni zawartej pod wykresem v(t) pozwala obliczyć drogę, jaką przebyło ciało
Jeśli ciało przed rozpoczęciem ruchu znajdowało się w stanie spoczynku ( $v_{0} = 0 \frac{m}{s}$ ) i porusza się ruchem jednostajnie przyspieszonym prostoliniowym, drogę oblicza się za pomocą wzoru:
$s = \frac{1}{2} \cdot a \cdot t^{2}$
gdzie: $s [m]$ – droga; $a [\frac{m}{s^{2}}]$ – przyspieszenie; $t <span data-specifier-type=]$ " separators="|">s – czas ruchu ciała.[
\ukryj-opis
R1HBZOah2ukBr
W ruchu jednostajnie przyspieszonym prostoliniowym przyrosty przebytej drogi w kolejnych sekundach ruchu mają się do siebie tak, jak następujące po sobie liczby nieparzyste.

Praca domowa

Polecenie 5.1

Narysuj wykres zależności drogi od czasu dla ciała poruszającego się ruchem jednostajnie przyspieszonym prostoliniowym z przyspieszeniem 2 $\frac{m}{s^{2}}$ w przedziale czasu od 0 do 10 s. Przyjmij, że wartość prędkości początkowej wynosiła $v_{o} = 0 \frac{m}{s}$ .

Polecenie 5.2

Narysuj wykres zależności prędkości od czasu dla ciała poruszającego się ruchem jednostajnie przyspieszonym z przyspieszeniem 10 $\frac{m}{s^{2}}$ w przedziale czasu od 0 do 8 s. Na podstawie otrzymanego wykresu oblicz drogę przebytą przez to ciało w przedziale czasu od 2 do 5 s.

Polecenie 5.3

* Narysuj wykres zależności wartości prędkości od czasu dla ciała, którego prędkość początkowa wynosiła 2 $\frac{m}{s}$ . Poruszało się ono jeszcze przez 10 sekund z przyspieszeniem o wartości 2 $\frac{m}{s^{2}}$ .

Wiesz, że pole pod wykresem v(t) jest równe drodze przebytej przez ciało. Zaznacz na wykresie drogę, jaką przebyłoby ciało, gdyby jego prędkość była równa prędkości początkowej równej 2 $\frac{m}{s}$ , oraz drogę, jaką przebyło ono dzięki wzrostowi wartości prędkości.
Na następnej lekcji przedstaw sposób na obliczanie drogi w ruchu jednostajnie przyspieszonym, jeżeli wartość prędkości początkowej jest różna od zera. Wskazówka: jaki kształt ma pole pod wykresem? Jak obliczyć pole powierzchni tej figury geometrycznej?

iMT8Y5NXq8_d5e605

Zadania

Ćwiczenie 1

RDG90x8Ozn0mx1

Ćwiczenie 2

R1BOO6xVEGui61

Uzupełnij zdanie tak, aby było prawdziwe.

Odcinki drogi przebyte w równych odcinkach czasu w ruchu jednostajnie przyspieszonym prostoliniowym bez prędkości początkowej mają się jak kolejne liczby .......................

Ruch jednostajnie przyspieszony prostoliniowy

Rozwiązywanie zadań dotyczących ruchu jednostajnie przyspieszonego prostoliniowego

Rysowanie i analiza wykresów zależności drogi i prędkości od czasu w ruchu jednostajnie przyspieszonym prostoliniowym

1. Zależność przyspieszenia od czasu

2. Zależność prędkości od czasu

3. Droga w ruchu jednostajnie przyspieszonym

Podsumowanie

Zadania