Figury płaskie
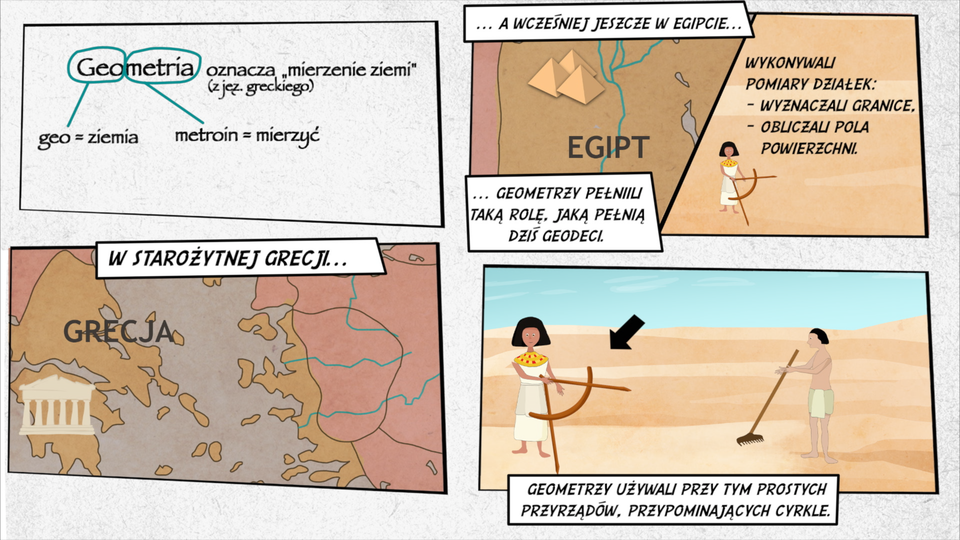
Słowo geometria pochodzi z języka greckiego i oznacza „mierzenie ziemi” ( to ziemia, to mierzyć). W starożytnej Grecji, a wcześniej jeszcze w Egipcie, geometrzy pełnili taką rolę, jaką dziś pełnią geodeci. Wykonywali pomiary działek – wyznaczali granice, obliczali pola powierzchni. Używali przy tym sznurów i prostych przyrządów, przypominających cyrkle. Działki egipskich chłopów były corocznie zalewane przez Nil, zatem geometrzy ciągle doskonalili swoje umiejętności, aby terminowo wykonać pilne prace.
Rozglądając się dokoła, zauważamy rozmaite obiekty trójwymiarowe. Opisując je, możemy określić ich długość, szerokość, wysokość lub głębokość. Takie obiekty to figury przestrzenne (bryły). Badaniem własności brył zajmuje się stereometria (z języka greckiego to przestrzeń).
Cienie brył (w geometrii zwane rzutami) mają kształt figur płaskich. Badaniem własności figur płaskich zajmuje się nauka zwana planimetrią (z języka greckiego to płaszczyzna, to mierzyć).
Film dostępny na portalu epodreczniki.pl
Animacja
Zastanów się, jak zmienia się cień obracającego się sześcianu.
Jak myślisz – jaką figurę płaską będzie przypominał cień sześcianu, na który popatrzymy z góry? A z boku?
Czy można tak umieścić sześcian, by patrząc z góry, widzieć sześciokąt?
Jakie inne figury płaskie przypominają ci cienie sześcianu?
Sprawdź swoje przypuszczenia.

Film dostępny na portalu epodreczniki.pl
Animacja 3D pokazuje obracający się sześcian, który pozostawia na płaszczyźnie różne odbicia.
Zauważamy, że cienie sześcianu mają najczęściej kształt wielokątów - czworokątów, sześciokątów lub pięciokątów.
Niektóre elementy figur przestrzennych także mają kształt figur płaskich.
Jakie figury płaskie można dostrzec na rysunkach?

Na liście nazwisk zapisanych na wieży Eiffla znajduje się nazwisko francuskiego matematyka, fizyka i chemika Gasparda Monge’a, żyjącego na przełomie i .
Monge opracował metodę odwzorowywania brył na prostopadłe względem siebie płaszczyzny. Metoda ta, zwana rzutami Monge, jest stosowana powszechnie do rozwiązywania wielu problemów geometrycznych.
Punkt, prosta, wzajemne położenie prostych
Film dostępny na portalu epodreczniki.pl
Animacja
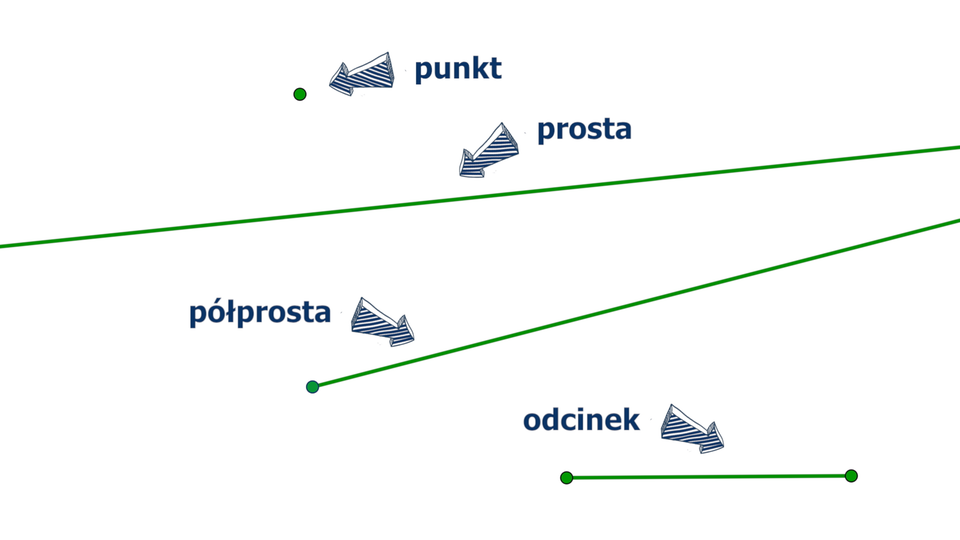
Najprostszą figurą geometryczną jest punkt.
Wszystkie pozostałe figury geometryczne składają się z punktów.
Punkty oznaczamy dużymi literami.
Modelem punktu może być kropka narysowana ołówkiem lub na przykład zmniejszający się obraz Księżyca widzianego ze statku kosmicznego.

Film dostępny na portalu epodreczniki.pl
Animacja
Przykładem figury, która składa się z nieskończenie wielu punktów, jest prosta.

Proste oznaczamy małymi literami, na przykład: , , , , , , .
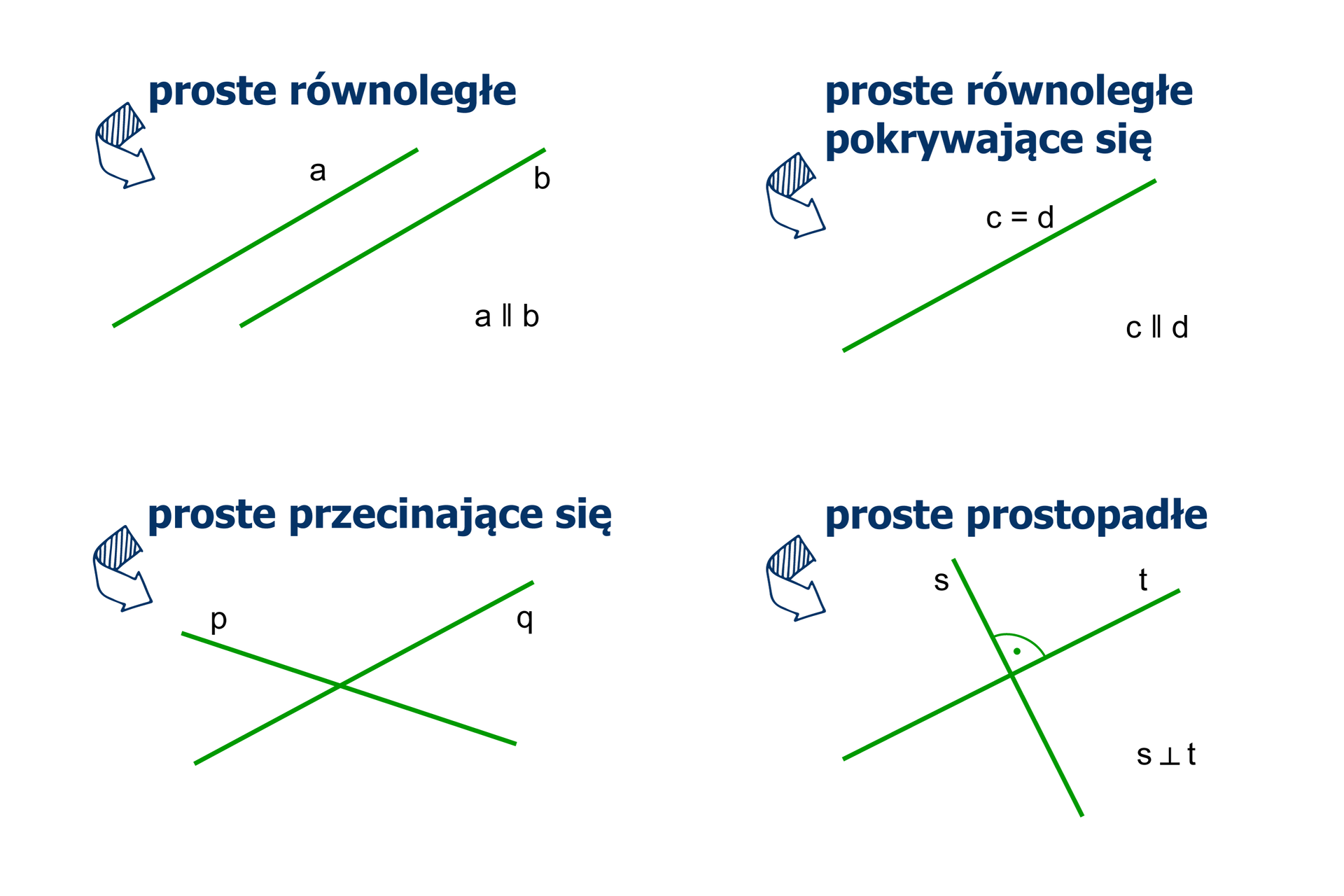
Dwie proste nazywamy równoległymi, jeśli nie mają punktów wspólnych lub mają nieskończenie wiele punktów wspólnych (pokrywają się).
Jeśli proste mają dokładnie jeden punkt wspólny, to mówimy, że przecinają się. Takie proste nazywamy prostymi przecinającymi się.
Jeśli proste przecinają się pod kątem prostym, wówczas nazywamy je prostopadłymi.
Przedstawmy konstrukcję prostej prostopadłej do danej prostej, poprowadzonej przez dany punkt.
Rozważymy dwa przypadki – punkt nie leży na danej prostej i punkt leży na prostej.
Przypadek
Dana jest prosta i punkt nieleżący na tej prostej.

Film dostępny na portalu epodreczniki.pl
Animacja
Opis konstrukcji
Kreślimy okrąg o środku w punkcie tak, aby przecinał prostą .
Punkty przecięcia okręgu z prostą oznaczamy i .
Rysujemy okręgi o jednakowych promieniach i o środkach w punktach i , tak aby jednym z punktów przecięcia okręgów był punkt .
Drugi z punktów przecięcia okręgów oznaczamy .
Rysujemy prostą przechodzącą przez punkty i . Prosta ta jest prostopadła do prostej .
Przypadek
Punkt leży na prostej .

Film dostępny na portalu epodreczniki.pl
Animacja
Opis konstrukcji
Rysujemy okrąg o środku w punkcie .
Punkty przecięcia okręgu z prostą oznaczamy i .
Kreślimy przecinające się okręgi o równych promieniach i środkach odpowiednio w punktach oraz .
Punkty przecięcia okręgów oznaczamy , .
Rysujemy prostą przechodzącą przez punkty , . Prosta ta jest prostopadła do prostej i przechodzi przez punkt .
Przedstawmy teraz konstrukcję prostych równoległych.
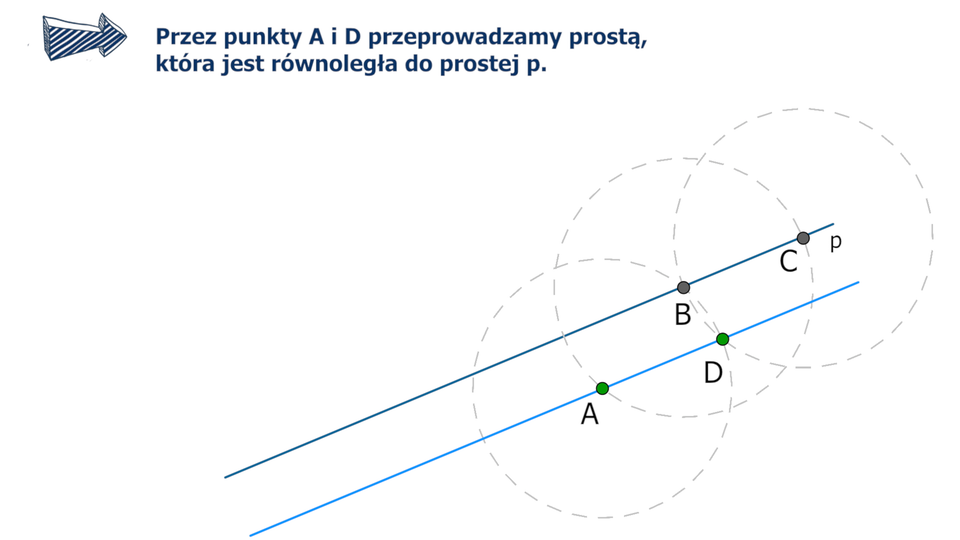
Dana jest prosta i punkt nieleżący na tej prostej. Skonstruujemy prostą równoległą do prostej przechodzącą przez punkt .
Film dostępny na portalu epodreczniki.pl
Animacja
Opis konstrukcji
Kreślimy okrąg o środku w punkcie i takim promieniu , aby okrąg przeciął prostą .
Jeden z punktów przecięcia okręgu z prostą oznaczamy .
Z punktu wykreślamy okrąg o promieniu .
Oznaczamy – punkt przecięcia tego okręgu z prostą .
Punkt przecięcia okręgu o środku w punkcie z okręgiem o środku w punkcie oznaczmy .
Przez punkty i przeprowadzamy prostą . Prosta ta jest równoległa do prostej .
Ile prostych przechodzi przez dany punkt? A przez dwa różne punkty?

Film dostępny na portalu epodreczniki.pl
Animacja
Przez jeden punkt przechodzi nieskończenie wiele prostych.
Przez dwa różne punkty przechodzi dokładnie jedna prosta.
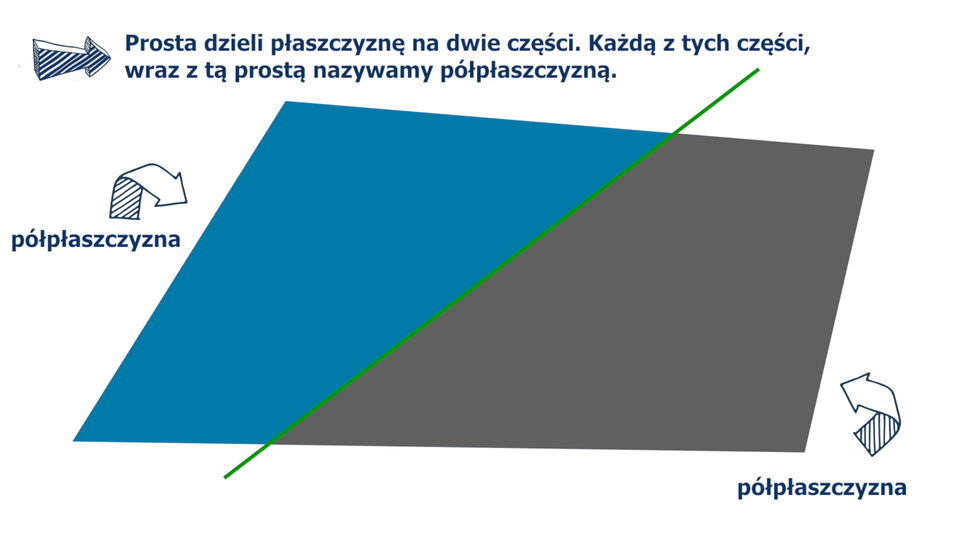
Półpłaszczyzna
Prosta dzieli płaszczyznę na dwie części. Każdą z nich wraz z tą prostą nazywamy półpłaszczyzną. Prosta ta jest brzegiem każdej z tych półpłaszczyzn.
Film dostępny na portalu epodreczniki.pl
Animacja
Jak myślisz – na ile części dwie proste mogą podzielić płaszczyznę? A trzy proste? Sprawdź swoje przypuszczenia.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DYcNX0b9A
Jaka jest najmniejsza, a jaka największa liczba części, na które trzy różne proste mogą podzielić płaszczyznę?
Półprosta, odcinek
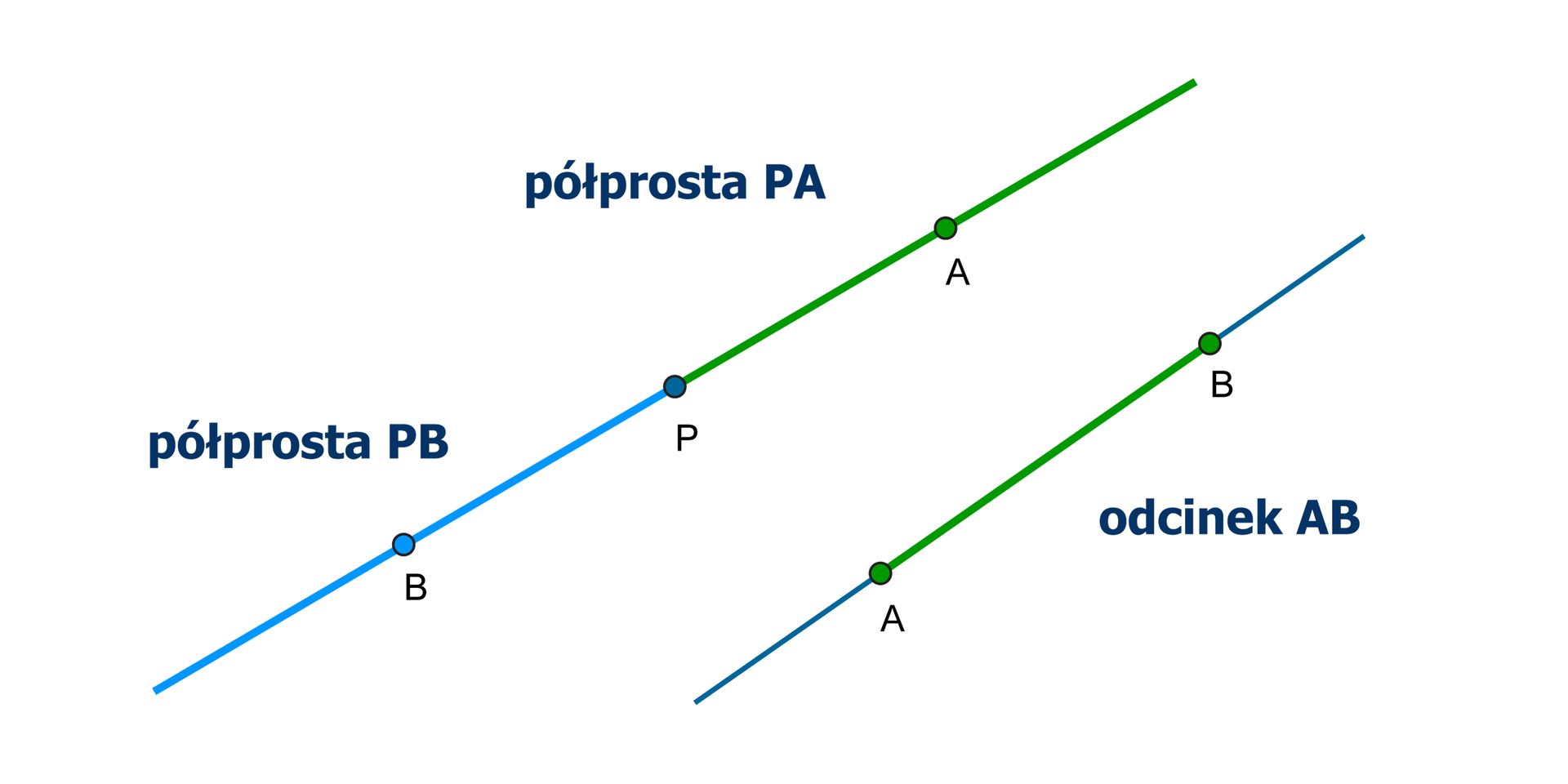
Punkt leżący na prostej dzieli ją na dwie części. Każdą z tych części, wraz z tym punktem nazywamy półprostą. Punkt ten jest początkiem każdej z półprostych.
Część prostej zawartej między dwoma punktami, wraz z tymi punktami, to odcinek.
Zmieniaj położenie punktów i na prostej tak, aby otrzymać prostą, odcinek, półprostą.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DYcNX0b9A
Obserwując położenie prostych i odcinków zawartych w prostych prostopadłych, zauważamy, że wszystkie półproste i odcinki zawarte w jednej z prostych prostopadłych są prostopadłe do każdej półprostej i każdego odcinka zawartych w drugiej półprostej.

Podobnie, wszystkie półproste i odcinki zawarte w jednej z prostych równoległych są równoległe do każdej półprostej i każdego odcinka zawartych w drugiej prostej.

Łamana
Narysuj otwartą kopertę. Nie odrywaj ołówka od papieru i nie prowadź go dwa razy po tym samym odcinku (oprócz początku i końca odcinka).

Łamana to figura zbudowana z odcinków w ten sposób, że koniec pierwszego odcinka jest początkiem drugiego odcinka, koniec drugiego odcinka jest początkiem trzeciego, itd.
Końce odcinków – to wierzchołki łamanej.
To jest łamana otwarta . Ma ona wierzchołków.
RPmKT5KAASjCv1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.To jest łamana zamknięta
RKvpkOc82cuN71 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Figury na rysunku zbudowane są z odcinków. Każdą z nich można narysować, nie odrywając ołówka od kartki papieru i nie rysując drugi raz po tej samej linii, są to przykłady łamanych.
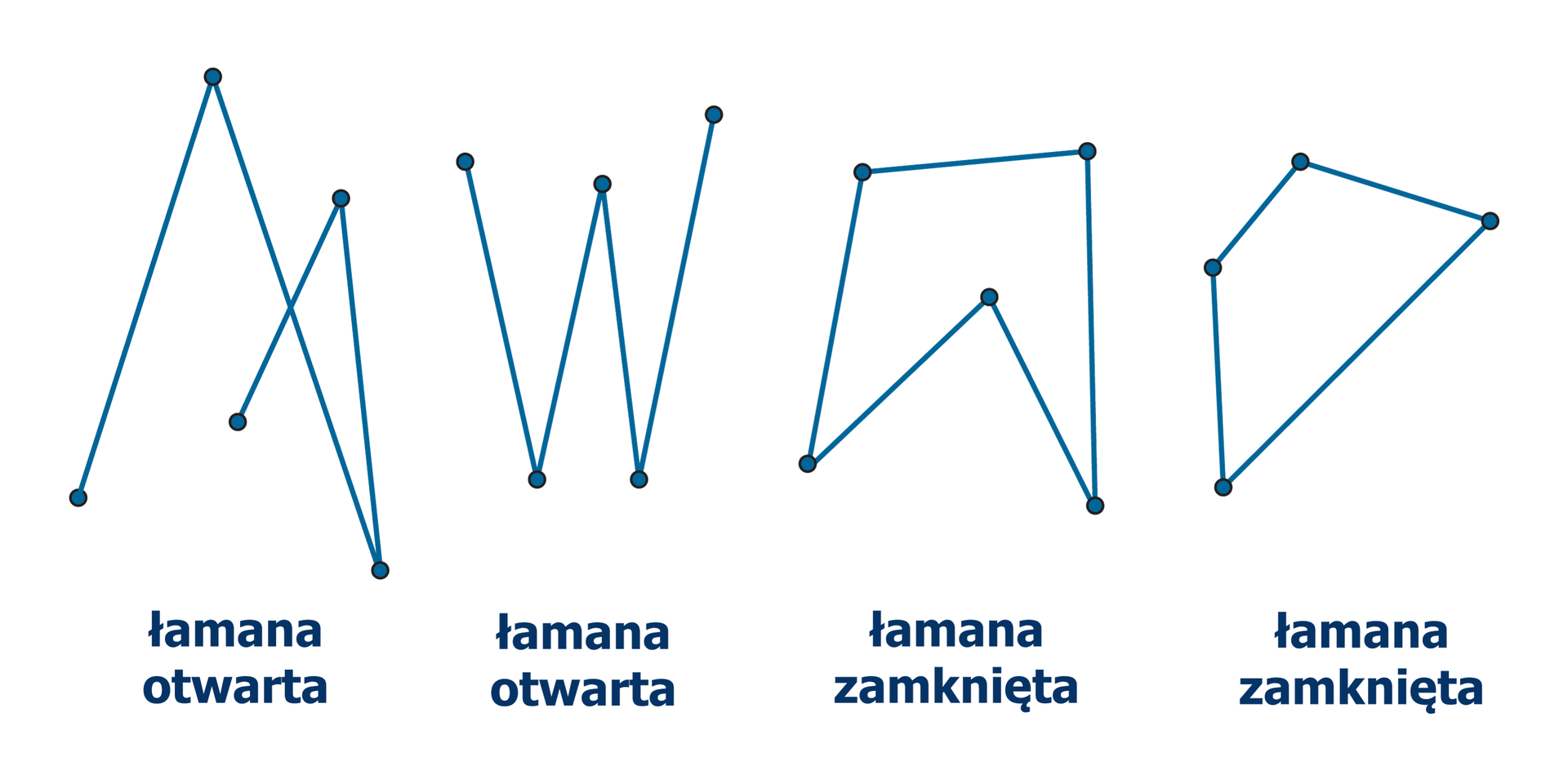
Czym różni się łamana zamknięta od otwartej?
Uzasadnij, że figury przedstawione na rysunku nie są łamanymi.

Z pewnością wiesz, że gazy zbudowane są z cząsteczek, które nieustannie się poruszają. Cząsteczka gazu porusza się po prostej do momentu zderzenia z inną cząsteczką. Zmienia wtedy kierunek ruchu, aż do następnego zderzenia. Można więc przyjąć, że tor ruchu tej cząsteczki ma kształt łamanej.
Przykłady figur płaskich
Modele jakich figur płaskich zauważasz na rysunkach?
Czy rozpoznajesz wśród nich wielokąty? A okręgi? A koła?

Narysuj dwa odcinki
mające jeden punkt wspólny
prostopadłe
równoległe
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Dwa odcinki, które leżą na jednej prostej mogą mieć punkty wspólne.
- Dwa odcinki, które leżą na jednej prostej są równoległe.
- Dwa odcinki, które leżą na jednej prostej mogą być prostopadłe.
Proste, które nie mają punktów wspólnych lub pokrywają się, to proste
- prostopadłe
- równoległe
- skośne
- przecinające się
Proste i są równoległe. Prosta jest prostopadła do prostej , a prosta jest równoległa do prostej .
Jak są położone względem siebie proste i ?
Jak położone są względem siebie proste i ?
Ile punktów wspólnych mają proste i ?
Punkt wyznacza na prostych i cztery półproste. Jak położone są proste i ? Gdzie leży punkt ?
Narysuj dwa różne punkty i . Przez punkt przeprowadź prostą , a przez punkt prostą tak, aby proste i
nie miały punktów wspólnych
przecinały się
były prostopadłe
Wykorzystując konstrukcje prostych prostopadłych i prostych równoległych, narysuj
prostokąt
równoległobok
Zaobserwuj w kształcie jakich figur płaskich mogą być cienie prostopadłościanu.
Narysuj prostą i zaznacz na niej punkty tak, aby punkt leżał między punktami i . Rozpatrz różne przypadki.
Mucha wędruje z punktu do punktu . Porusza się tylko po liniach kratek w dół i w prawo. Musi przejść przez punkt . Długość jednej kratki jest równa .
Zaznacz kilka dróg, którymi może się poruszać mucha.
Znajdź długość każdej z nich.
Jaką długość ma najkrótsza z możliwych dróg?
R1VhEKMwu67tS1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Narysuj łamaną, której
boki są prostopadłe
dokładnie dwa boki są równoległe
każdy bok ma inną długość
boki są prostopadłe, ale ich długości nie są równe
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Z odcinków długości , , można zbudować łamaną zamkniętą.
- Jeśli łamana zamknięta ma cztery boki to jej boki mogą być bokami kwadratu.
- Z odcinków długości , , można zbudować łamaną otwartą.
Dokończ poniższe zdanie.
Łamana zwyczajna zamknięta, która ma najmniejszą liczbę boków jest brzegiem … .
Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.
- Przez dwa różne punkty można poprowadzić tylko dwie różne proste.
- Półprosta ma początek, ale nie ma końca.
- Końce odcinka nie należą do tego odcinka.
- Dwie proste przecinające się mogą mieć dwa punkty wspólne.
Czy można zbudować łamaną zamkniętą złożoną z trzech odcinków o długościach , , ?
Znajdź informacje na temat Gasparda Monge i zastosowania wynalezionej przez niego metody rzutowania obiektów na lub płaszczyzny wzajemnie do siebie prostopadłe.



