Wyznaczanie gęstości materii
Być może zauważyłeś, że czasem ciało o niewielkich rozmiarach ma dużą masę, a ciała o sporych rozmiarach (np. pudło styropianowe) możemy łatwo podnieść, bo ich masa jest niewielka. Aby to wyjaśnić, wprowadzimy pojęcie gęstości ciała. Pozwoli ci ono zrozumieć opisaną poniżej sytuację i wiele innych zagadnień.

Uwaga: ze względu na swoje trujące właściwości, rtęć nie może być używana w doświadczeniach przeprowadzanych w szkole.
stwierdzić, że materia ma budowę cząsteczkową;
dokonać podziału materii na trzy stany skupienia: stały, ciekły i gazowy;
stwierdzić, że masa jest miarą ilości materii;
podać definicję objętości ciała.
obliczać gęstość ciała;
posługiwać się pojęciem gęstości ciała, potrzebnym do analizowania zjawisk;
wyrażać gęstość w jednostkach układu SI;
wykonywać działania na jednostkach gęstości (w tym: zamieniać jednostki);
uzasadniać, dlaczego ciała zbudowane z różnych substancji mają różną gęstość;
korzystać ze związku miedzy masą, gęstością i objętością ciała do wykonywania różnych obliczeń;
porównywać gęstości różnych substancji, zamieszczone w tablicach wielkości fizycznych.
1. Rozmiary ciał a ich masa
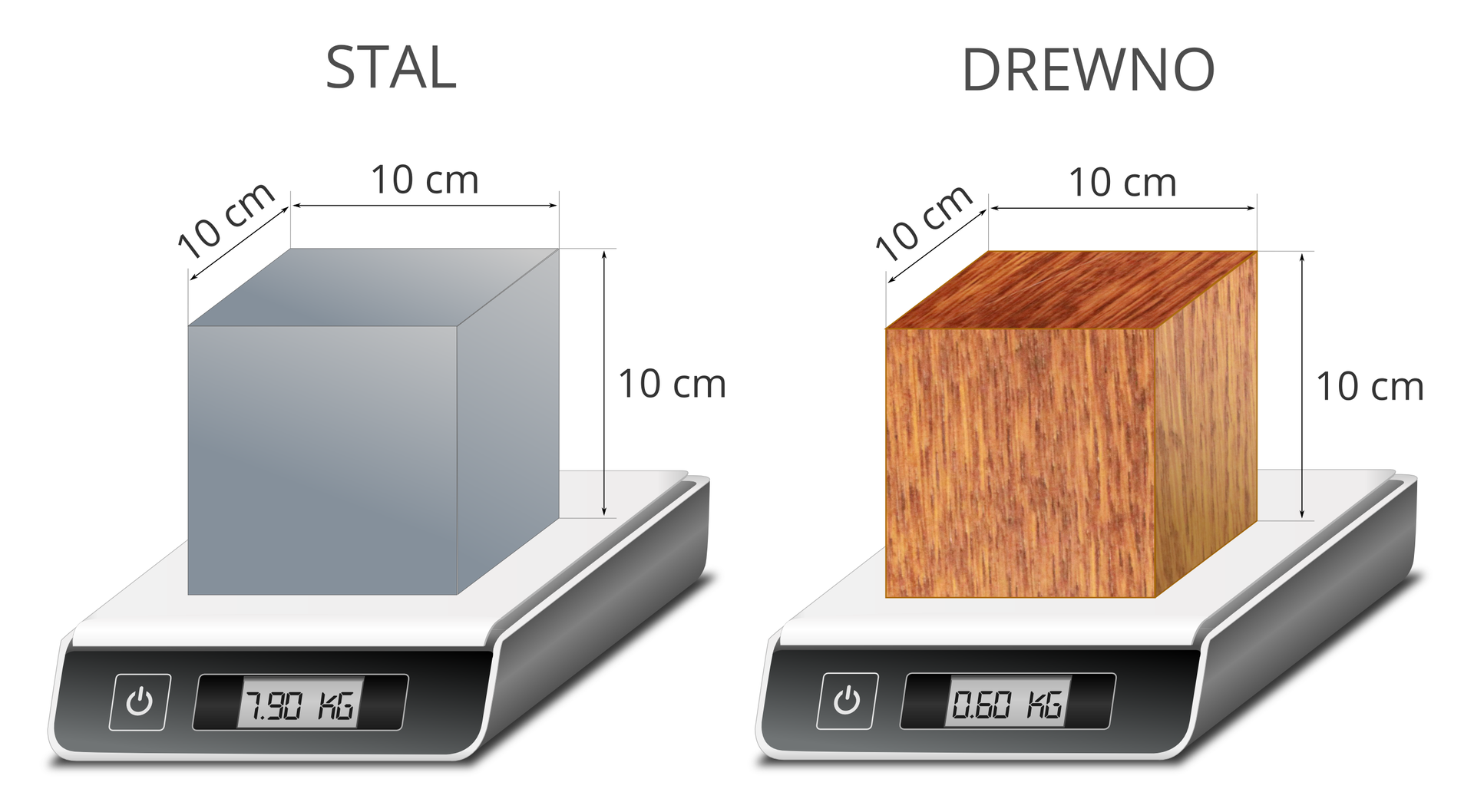
Niekiedy zaskakuje cię ciężar pewnych przedmiotów, np. gdy niesiesz dwie płyty (styropianową i gipsowo‑kartonową) o tych samych rozmiarach, czujesz, że ich masy zdecydowanie się różnią. W codziennym życiu możesz się także przekonać, że drewniany sześcian jest lżejszy od sześcianu ze stali o tym samym kształcie i identycznym rozmiarze.
Z drugiej strony, przedmioty o różnych rozmiarach mogą mieć taką samąmasęmasę. Trudno to przewidzieć bez znajomości materiałów, z których dane przedmioty zostały wykonane. Największa bryła została zrobiona ze styropianu, średnia z korka, a najmniejsza ze stali.
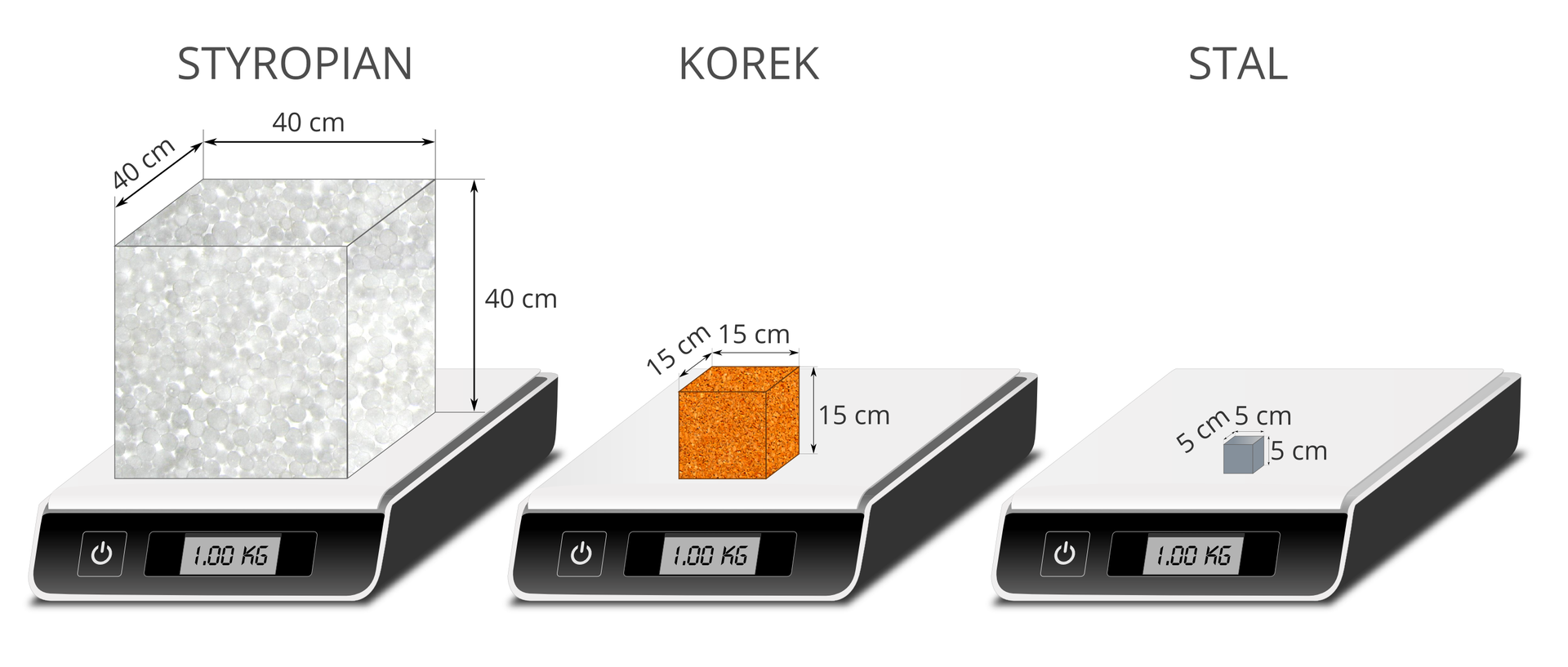
Dzięki odpowiedniemu doborowi wymiarów wszystkie pokazane na rysunku sześciany ma masę .
Masa ciała zależy zarówno od materiału, z jakiego zostało ono wykonane, jak i od jego wymiarów (objętości).
Przeczytaj poniższe zdania. Które z nich są prawdziwe, a które fałszywe?
| Prawda | Fałsz | |
| Ciała o tych samych wymiarach muszą posiadać zawsze taką samą masę. | □ | □ |
| Ciała o tych samych wymiarach mogą mieć różną masę. | □ | □ |
| Ciała o tej samej masie muszą mieć zawsze identyczne wymiary. | □ | □ |
2. Objętość
ObjętośćObjętośćto wielkość fizyczna, która jest miarą przestrzeni zajmowanej przez dane ciało. W układzie SI jednostką objętości jest metr sześcienny. Spróbuj wyobrazić sobie kostkę (lub pokaż ją za pomocą rąk) o wymiarach na na . Na co dzień używamy mniejszych jednostek takich jak decymetry sześcienne (litry) i centymetry sześcienne (mililitry). Wyobraź sobie lub pokaż za pomocą rąk kostkę o objętości (wymiary na na ).
Jak wyznaczyć objętość ciała o dowolnym kształcie?
Film dostępny na portalu epodreczniki.pl
Wyznaczanie objętości ciał o dowolnym kształcie
Za pomocą metody opisanej w filmie, wyznacz objętość ciała o nieregularnym kształcie. Może to być np. duża śruba lub łyżeczka do herbaty.
Po obejrzeniu filmu zastanów się, co wpływa na zmianę objętości wody wypieranej przez klucz zawieszony na łańcuszku. Co trzeba zrobić, aby możliwie dokładnie wyznaczyć tą metodą objętość śruby lub łyżeczki?
Zaznacz poprawną odpowiedź.
- Objętość informuje o tym, jak dużą przestrzeń zajmuje ciało.
- Objętość informuje o tym, ile wody zmieści się w danym ciele.
- Objętość informuje o tym, jak ciężkie jest ciało.
3. Zależność masy od objętości
Czy ciała o większej masie mają większą objętość, a ciała o większej objętości – większą masę? Aby się o tym przekonać, przeprowadź prosty eksperyment.
Czy przedmiot wykonany z takiego samego materiału, ale mający większą objętość, ma większą masę?
Im większa jest objętość ciał wykonanych z tego samego materiału, tym większa jest ich masa. Stosunek masy do objętości pozostaje stały.
zestaw odważników 200 g, 100 g, 50 g i 20 g, wykonanych z tego samego materiału;
wyskalowane naczynie (menzurka);
woda.
Za pomocą menzurki zmierz objętość poszczególnych odważników.
Wyniki pomiarów zapisz w tabeli.
Przerysuj poniższą tabelę do zeszytu i ją uzupełnij..
Zilustruj graficznie wyniki pomiarów. Wykonaj wykres zależności masy ciała od jego objętości m(V). Najpierw narysuj oś poziomą, która będzie przedstawiała zmiany objętości wyrażone w centymetrach sześciennych, potem zaś – oś pionową. Zaznacz na niej wartości masy wyrażone w gramach. Na tak przygotowany układ współrzędnych nanieś odpowiednie punkty (posłuż się wartościami zapisanymi w tabeli).
Z przeprowadzonego doświadczenia wynika, że masa ciała rośnie wraz ze wzrostem objętości – masa rośnie tyle razy, ile rośnie objętość. Dla danej substancji stosunek masy ciała do jego objętości jest stały.
Doświadczenie pokazało, że masa ciała zmienia się wraz ze zmianą jego objętości. Dwukrotny wzrost objętości ciała powoduje dwukrotny wzrost jego masy, trzykrotny wzrost objętości ciała – trzykrotny wzrost jego masy itd. Oznacza to, że dla ciał wykonanych z tego samego materiału iloraz masy i objętości musi pozostać stały.
Warto zaznaczyć, że rozpatrujemy tylko ciała o budowie jednorodnej (substancja jest rozłożona równomiernie w przestrzeni zajmowanej przez ciało, np. kostkę ze stali). Nie bierzemy pod uwagę ciał mających w środku duże puste przestrzenie (np. pudełka wykonanego z blachy stalowej).
Które odpowiedzi są prawdziwe, a które fałszywe?
| Prawda | Fałsz | |
| Stosunek masy do objętości dla ciał wykonanych z tej samej substancji jest zawsze taki sam. | □ | □ |
| Stosunek masy do objętość dla ciał wykonanych z różnych substancji zawsze będzie taki sam. | □ | □ |
| Wraz ze wzrostem objętości ciał wykonanych z tego samego materiału, rośnie ich masa. | □ | □ |
4. Gęstość ciał
Iloraz masy i objętości danego ciała nazywamy jegogęstościągęstością. Z doświadczenia z poprzedniego paragrafu wiesz już, że w przypadku ciał wykonanych z tego samego materiału iloraz masy i objętości pozostaje stały. Gęstość jest więc wielkością charakterystyczną dla danej substancji. Jednostką gęstości w układzie SI jest kg na metr sześcienny. Oznaczamy ją literą d lub rzadziej grecką literą rho („ro”).
– wartość ilorazu masy (m) ciała i jego objętości (V) stała dla danej substancji.
Wzór na gęstość:
gdzie: d – gęstość; m – masa ciała; V – jego objętość.
Gdy podajesz gęstość w kilogramach na metr sześcienny, dowiadujesz się, jaką masę w kilogramach ma jeden metr sześcienny substancji.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DhnIhGgtF
Podstawową jednostką gęstości jest kilogram na metr sześcienny. W praktyce dla wygody dość często wyrażamy gęstości ciał w mniejszych jednostkach, np. . W takiej sytuacji musimy skorzystać z zależności między jednostkami.
Film dostępny na portalu epodreczniki.pl
Demonstrator na tle tablicy. Gęstość, tak jak i inne wielkości fizyczne, można wyrazić w różnych jednostkach. Najczęściej używane to: kilogram na metr sześcienny i gram na centymetr sześcienny. Zobaczmy, w jaki sposób przeliczamy te jednostki. Mamy tu do czynienia z jednostkami masy, kilogramami i gramami oraz jednostkami objętości: metrami sześciennymi i centymetrami sześciennymi. Z jednostkami masy jest łatwo. Pamiętamy, że 1 kilogram to 1000 gramów. Tym samym 1 gram to jedna tysięczna kilograma. Z objętością jest nieco trudniej. Pamiętamy, że 1 metr to 100 centymetrów, czyli 1 cm to jedna setna metra. Ale czy to oznacza, że 1 metr sześcienny to 100 centymetrów sześciennych? Nic bardziej mylnego!Pomóżmy sobie rysunkiem. 1 metr sześcienny to objętość sześcianu o boku 1 m, czyli 100 cm. 1 centymetr sześcienny to objętość sześcianu o boku 1 cm, czyli kosteczki zamalowanej na czerwono. Ile takich kosteczek mieści się w dużym sześcianie? Łatwo to policzyć: wszerz jest 100 takich kosteczek, w głąb również 100 i na wysokość także 100. Razem więc zmieści się w dużej kostce sto razy sto razy 100 małych kosteczek. A więc 1 metr sześcienny to milion centymetrów sześciennych. Na odwrót: jeden centymetr sześcienny to jedna milionowa metra sześciennego. Teraz możemy wrócić do przeliczenia jednostek gęstości. Przeliczmy np. 300 kilogramów na metr sześcienny na gramy na cm sześcienny. 300 przepisujemy, 1 kilogram to 1000 gramów, a 1 metr sześcienny to milion cm sześciennych. Teraz tylko upraszczamy, skracając ułamek, i otrzymujemy wynik trzy dziesiąte grama na centymetr sześcienny.
Gęstość ma związek z utrzymywaniem się ciał na powierzchni cieczy – w zależności od tego, jaka jest gęstość ciała w porównaniu z gęstością cieczy, ciało będzie tonąć lub utrzymywać się powierzchni cieczy. Wynika to z prawa Archimedesaprawa Archimedesa.
Bloczki z gazobetonu (betonu komórkowego), używane do budowy domów, są lżejsze niż te betonowe (o tych samych rozmiarach), ponieważ zawierają dużo pęcherzyków powietrza. Dzięki temu gęstość betonu komórkowego jest mniejsza niż gęstość zwykłego betonu.
Gęstość substancji zmienia się wraz ze zmianą temperatury i/lub ciśnienia.
Adrian, Lech i Marek rozmawiają o znaczeniu gęstości. Zapoznaj się z opinią każdej z osób i zaznacz wszystkie poprawne odpowiedzi.
- Adrian: W pewnej objętości wody jest więcej cząsteczek niż w takiej samej objętości lodu.
- Lech: W pewnej objętości wody jest mniej cząsteczek niż w takiej samej objętości lodu.
- Marek: W danej objętości wody i lodu jest tyle samo cząsteczek.
5. Gęstości różnych substancji
W wielu sytuacjach gęstość jest cenną wskazówką pozwalającą rozpoznać, z jakiego materiału jest wykonane dane ciało. Aby ułatwić to zadanie, stworzono tabele gęstości wybranych substancji. Pamiętajmy jednak, że wiele substancji ma zbliżone gęstości. Właściwą klasyfikację komplikują również stopy o różnym składzie chemicznym.
Ciało | |
grafit | 2300–2720 |
gips | 2320 |
krzem | 2330 |
beryl | 2700 |
aluminium | 2720 |
kwarc | 2750 |
Zapoznaj się z tablicami gęstości wybranych ciał stałych w temperaturze 20°C. Poniżej umieszczono tablice gęstości ciał stałych, cieczy i gazów.
Ciało stałe | |
cynk | 7131 |
drewno topoli | 350–400 |
drewno lipy | 320–590 |
drewno sosny | 370–600 |
drewno dębu | 600–900 |
duraluminium | 2790 |
kwarc | 2300–2700 |
miedź | 8960 |
mosiądz | 8200–8950 |
ołów | 11 336 |
platyna | 21 410 |
stal nierdzewna | 8100 |
złoto | 19 320 |
żelazo kute | 7800–7900 |
lód (0°C) | 920 |
sól kamienna | 2160 |
Ciecze | |
alkohol etylowy | 791 |
ciekły azot (–196°C) | 808 |
benzyna | 700 |
eter | 720 |
gliceryna | 1260 |
nafta | 800 |
oliwa | 920 |
rtęć | 13 550 |
woda destylowana (4°C) | 1000 |
ciekły wodór (–253°C) | 71 |
Gazy | |
argon | 1,784 |
azot | 1,250 |
chlor | 3,22 |
dwutlenek węgla | 1,98 |
etan | 1,36 |
hel | 0,178 |
metan | 0,717 |
powietrze | 1,293 |
tlen | 1,429 |
wodór | 0,09 |
Podsumowanie
Masa ciała zależy zarówno od materiału, z jakiego zostało ono wykonane, jak i od objętości tego ciała.
Objętość to wielkość fizyczna, która jest miarą przestrzeni zajmowanej przez dane ciało.
W przypadku ciał wykonanych z tego samego materiału iloraz masy i objętości jest stały.
Gęstość (d) to wartość ilorazu masy (m) i objętości (V). Gęstość oblicza się za pomocą wzoru:
gdzie: m – masa ciała; V – jego objętość.
Gęstość podana w kilogramach na metr sześcienny to informacja, jaką masę w kilogramach ma jeden metr sześcienny substancji.
Na podstawie pobranej próbki danego materiału i wyznaczenia jego gęstości możemy spróbować określić rodzaj substancji, z jakiej został wykonany ten materiał. Korzystamy wtedy z tabeli gęstości wybranych substancji.
Zamień jednostki i wpisz odpowiednią wartość:
Zamień jednostki i wpisz odpowiednią wartość:
= ......
= ......
= ......
= ......
Staś, Zuzia i Marek rozmawiają o najsilniejszym uczniu w szkole, który jest w stanie podnieść ciało o masie . Czy temu uczniowi udałoby mu się podnieść 6‑litrowe naczynie wypełnione rtęcią? Gęstość rtęci wynosi .
Oblicz gęstość ciała, które po zanurzeniu w wodzie wypełniającej częściowo menzurkę zmieniło jej poziom z do . Przyjmij, że masa ciała wynosiła 50,6 g. Wynik podaj z dokładnością do dwóch cyfr znaczących.
O ile wzrośnie masa samochodu, gdy pusty zbiornik paliwa o objętości 40 l całkowicie wypełnimy benzyną? Gęstość benzyny odczytaj z tablicy gęstości wybranych cieczy.
Zajrzyj do zagadnień pokrewnych:
Masa i ciężar ciałaMasa i ciężar ciała
Pomiary w fizyce. Niepewność pomiaru. Przeliczanie wielokrotności i podwielokrotnościPomiary w fizyce. Niepewność pomiaru. Przeliczanie wielokrotności i podwielokrotności
Słowniczek
– miara ilości substancji; zależy zarówno od materiału, z jakiego zostało wykonane, jak i od wymiarów danego ciała.
– wielkość fizyczna, która jest miarą przestrzeni zajmowanej przez dane ciało.
– wartość ilorazu masy (m) ciała i jego objętości (V).
Zadania
Które informacje, dotyczące wyznaczania objętości ciał o nieregularnych kształtach są prawdziwe, a które fałszywe?
| Prawda | Fałsz | |
| Nie da się wyznaczyć objętości takiego ciała bez poznania jego dokładnych wymiarów. | □ | □ |
| Objętość ciała o nieregularnych kształtach można wyznaczyć za pomocą menzurki. | □ | □ |
| Bez użycia skomplikowanej aparatury badawczej nie jesteśmy w stanie wyznaczyć objętości takich ciał. | □ | □ |
Asia, Marcel i Darek rozmawiają o możliwości sprawdzenia czy królewska korona została wykonana z czystego złota. Zapoznaj się z opinią każdej z osób i zaznacz wszystkie poprawne odpowiedzi.
- Asia: Można sprawdzić czy korona została wykonana z czystego złota, po wyznaczeniu jej gęstości i porównaniu jej z wartościami tablicowymi gęstości złota.
- Marcel: Nie jesteśmy w stanie sprawdzić, czy korona została wykonana ze szczerego złota bez wykonania analizy chemicznej.
- Darek: Jesteśmy w stanie sprawdzić, z czego wykonana jest korona po zważeniu jej.