5. Liczby całkowite - podsumowanie - Działania na liczbach całkowitych

RDonibVNM069B

5. Liczby całkowite - podsumowanie

R1Vv2Pn1EAXUE1

Zdjęcie przedstawia świnkę - skarbonkę oraz rozrzucone wokół niej monety. — Źródło: Skitterphoto, domena publiczna. https://www.pexels.com/pl-pl/.

Koncepcja liczb ujemnych powstała w $I$ wieku p. n. e w Chinach.

W $VII$ wieku indyjski astronom i matematyk Brahmagupta napisał dzieło, którego tytuł można przetłumaczyć jako „Odsłona wszechświata”. W dziele tym opisał m.in. zasady działań na „majętnościach” i „długach”, czyli określił reguły działań na liczbach dodatnich, ujemnych i zerze. Podał też tam definicję zera. Dzieło to jest uznawane za pierwsze, w którym opisano działania na tych liczbach.

W tym materiale znajdziesz zebrane najważniejsze informacje o działaniach na liczbach całkowitych, w tym całkowitych ujemnych. Wykonasz też ćwiczenia, które utrwalą i rozszerzą twoje umiejętności.

Ważne!

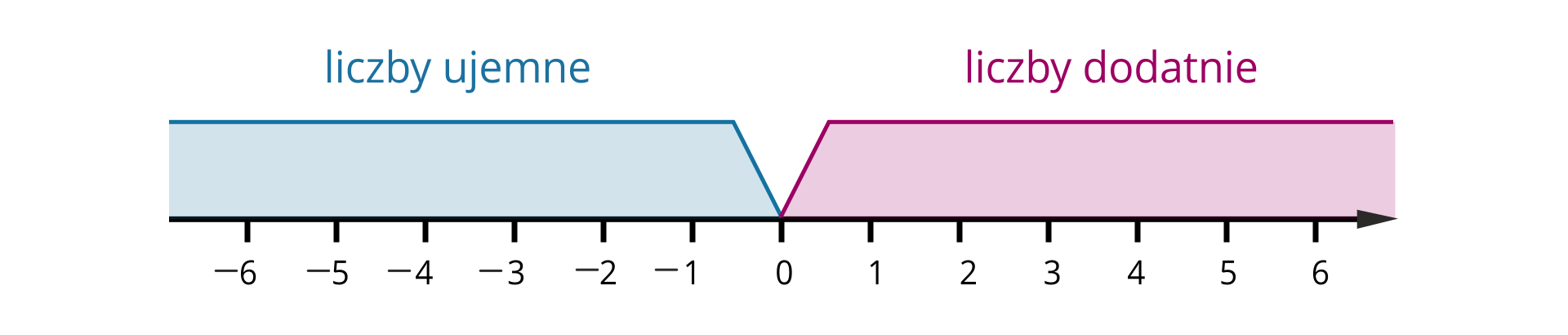
Liczby $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $\dots$ , $\dots$ to liczby całkowite dodatnie.
Liczby $- 1$ , $- 2$ , $- 3$ , $- 4$ , $\dots$ , $\dots$ to liczby całkowiteujemne.
Liczba $0$ nie jest liczbą dodatnią, ani ujemną.
Liczby $0$ , $1$ , $2$ , $3$ , $4$ , $5$ , $6$ , $\dots$ , $\dots$ to liczby całkowite nieujemne.
Liczby $0$ , $- 1$ , $- 2$ , $- 3$ , $- 4$ , $\dots$ , $\dots$ to liczby całkowite niedodatnie.

Liczby dodatnie na osi liczbowej położone są na prawo od zera, a liczby ujemne na lewo.

R4x9s1v36gurl

Oś pozioma ze zwrotem w prawo. Zaznaczone są na niej wartości od -6 do 6, rosnące co 1. Obszar od zera w lewą stronę zaznaczono kolorem niebieskim i podpisano jako liczby ujemne. Obszar od zera w prawą stronę zaznaczono kolorem różowym i podpisano jako liczby dodatnie. — Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ważne!

Odległość liczby od zera na osi liczbowej nazywamy wartością bezwzględną tej liczby.

Na przykład odległość liczby $6$ od zera jest równa $6$ . Zapisujemy:

|6| = 6

Przykład 1

Określimy wartość bezwzględną każdej z liczb: $5$ , $0$ , $- 7$ , $- 11$ .

|5| = 5

|0| = 0

|- 7| = 7

|- 11| = 11

Aby dodać dwie liczby całkowite ujemne, dodajemy ich wartości bezwzględne i przed wynikiem stawiamy znak minus. Aby dodać dwie liczby całkowite różnych znaków, odejmujemy od większej wartości bezwzględnej, mniejszą wartość bezwzględną, a przed wynikiem stawiamy znak, jaki ma liczba o większej wartości bezwzględnej.

Przykład 2

Wykonamy dodawanie.

- 1 + (- 2) = - 3

- 8 + (- 4) = - 12

$- 4 + 6 = 6 - 4 = 2$ , bo $|6| > |- 4|$
$- 10 + 2 = - 8$ , bo $|- 10| > |2|$
$- 3 + 3 = 0$ , bo $|- 3| = |3|$

Odejmowanie liczby można zastąpić dodawaniem liczby przeciwnejliczby przeciwneliczby przeciwnej.
Na przykład:

- 8 - 4 = - 8 + (- 4) = - 12

7 - 10 = 7 + (- 10) = - 3

Aby pomnożyć (podzielić) liczby całkowite, różne od zera, należy pomnożyć (podzielić) ich wartości bezwzględne i przed wynikiem postawić znak:

plus, jeżeli w iloczynie (ilorazie) występuje parzysta ilość liczb ujemnych,
minus, jeżeli w iloczynie (ilorazie) występuje nieparzysta ilość liczb ujemnych.

Przykład 3

Kolumna pierwsza	Kolumna druga
$- 2 \cdot (- 3) \cdot 10 = 60$	$- 10 : (- 2) = 5$
$5 \cdot (- 1) \cdot (- 3) \cdot (- 2) = - 30$	$- 4 : 2 = - 2$
$0 \cdot (- 2) = 0$	$0 : (- 2) = 0$
$(- 1) \cdot 6 \cdot (- 2) \cdot 3 = 36$	$- 12 : (- 2) : (- 3) = - 2$

Reguły dotyczące wykonywania działań na liczbach całkowitych są takie same, jak reguły wykonywania działań na liczbach naturalnych.

Przykład 4

Monika pożyczyła od Magdy $10 zł$ , od Karola $6 zł$ i od Wandy $12 zł$ . Od dziadka dostała $15 zł$ , a od mamy taką kwotę, że obie te kwoty łącznie wystarczyły jej na spłatę zaciągniętych długów. Obliczymy, jaką kwotę dostała Monika od mamy.

Obliczymy najpierw, ile jeszcze pieniędzy potrzebowała Monika, po otrzymaniu pieniędzy od dziadka.

15 - (10 + 6 + 12) = 15 - 28 = - 13

Monika potrzebowała jeszcze $13 zł$ , zatem mama dała jej właśnie taką kwotę.

A teraz sprawdź swoją wiedzę i umiejętności rozwiązując zadania.

Ćwiczenie 1

Zagraj w grę. Zaznacz prawdziwe równości oraz prawdziwe nierówności.

RbXO0Lr1F7Vh4

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Etap pierwszy:

R1XLgLJ4GEFM2

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Etap drugi:

R179gC1HSQIyv

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Ćwiczenie 2

Oblicz.

$- 6 : 3 + 4 \cdot 5 - (- 3) \cdot (- 6)$
$(- 7 - 8 - 9) - (- 24)$
$(- 3 + 7 + 3 - 7) \cdot 10$
$(10 - 9) (9 - 10)$

$- 6 : 3 + 4 \cdot 5 - (- 3) \cdot (- 6) = - 2 + 20 - 18 = 18 - 18 = 0$
$(- 7 - 8 - 9) - (- 24) = - 24 + 24 = 0$
$(- 3 + 7 + 3 - 7) \cdot 10 = 0 \cdot 10 = 0$
$(10 - 9) (9 - 10) = 1 \cdot (- 1) = - 1$

Ćwiczenie 3

Porównaj liczby.

$- 12$ i $10$
$- 8$ i $10$
$- 9$ i $- 12$
$0$ i $- 4$

$- 12 < 10$
$- 8 < 10$
$- 9 > - 12$
$0 > - 4$

Ćwiczenie 4

Oblicz iloczyn wszystkich liczb niedodatnich spośród liczb: $19$ , $(- 19)$ , $(- 5)$ , $0$ , $11$ , $14$ , $(- 24)$ .

Iloczyn liczby całkowitej i liczby $0$ jest równy $0$ .

$(- 19) \cdot (- 5) \cdot (- 24) \cdot 0 = 0$

Ćwiczenie 5

R1ZYgtVR8bSEC

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

ROhAO3Y0015um

Ćwiczenie 6

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RD2dvL4dVLtwG

Ćwiczenie 7

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RIDvsHqvB5P2p

Ćwiczenie 8

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RLNig0gYMZhIk

Ćwiczenie 9

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R15MRcBbtDc2j

Ćwiczenie 10

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

RWNIIRvounZAF

Ćwiczenie 11

Źródło: GroMar Sp. z o.o., licencja: CC BY 3.0.

Rzn9F8nsBhJJ6

Ćwiczenie 12

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R17jUAj0FM5qq

Ćwiczenie 13

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RNSHIRMOvnyfy

Ćwiczenie 14

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R124JStp3oB5d

Ćwiczenie 15

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 16

Uporządkuj liczby: $4$ , $0$ , $(- 2)$ , $11$ , $(- 8)$ , $(- 3)$ , $(- 4)$ od najmniejszej do największej.

$- 8 < - 4 < - 3 < - 2 < 0 < 4 < 11$

Ćwiczenie 17

Sumę liczb $(- 6)$ i $(- 9)$ pomnóż przez różnicę tych liczb i wynik podziel przez $(- 5)$ .

$\frac{[- 6 + (- 9)] [- 6 - (- 9)]}{- 5} = \frac{(- 6 - 9) (- 6 + 9)}{- 5} = \frac{- 15 \cdot 3}{- 5} = \frac{- 45}{- 5} = 9$

RWp63fSFitfES

Ćwiczenie 18

Na początku kwietnia pan Piotr miał na koncie bankowym

1000 zł

. W ciągu pierwszego tygodnia najpierw wypłacił

500 zł

, a następnie jeszcze

550 zł

. Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Pod koniec pierwszego tygodnia stan konta pana Piotra wynosił Tu uzupełnij

zł

.W drugim tygodniu pan Piotr najpierw wpłacił na konto

750 zł

, a następnie wypłacił

600 zł

. Pod koniec drugiego tygodnia miał na koncie Tu uzupełnij

zł

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Gqgo6f5xRB5

Ćwiczenie 19

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 20

Dzisiaj rano temperatura powietrza w Krakowie wynosiła $- 10 ° C$ . W Warszawie była o $4 ° C$ wyższa niż w Krakowie. W Poznaniu temperatura powietrza była o $7 ° C$ niższa niż w Warszawie.

W którym z miast – Poznaniu czy Krakowie temperatura powietrza była wyższa i o ile stopni Celsjusza?

Obliczamy temperaturę powietrza w każdym z miast.

Kraków: $- 10 ° C$
Warszawa: $- 10 ° C + 4 ° C = - 6 ° C$
Poznań: $- 6 ° C - 7 ° C = - 13 ° C$

Obliczamy różnicę temperatur.

|- 13| - |- 10| = 3

Temperatura powietrza była w Poznaniu niższa niż w Krakowie o $3 ° C$ .

Ćwiczenie 21

W turnieju brały udział dwie czteroosobowe drużyny z dwóch klas piątych. Każdy z zawodników mógł zdobyć dla drużyny punkty dodatnie lub ujemne. Zwyciężyła ta drużyna, która łącznie zdobyła więcej punktów.

Oto tabela z wynikami.

Drużyna klasy $V a$	Liczba punktów	Drużyna klasy $V b$	Liczba punktów
Kasia	$8$	Marysia	$- 5$
Wojtek	$1$	Filip	$4$
Ola	$- 2$	Julka	$3$
Kuba	$- 3$	Maciek	$- 2$

R1SnYWlvIfmq8

Uzupełnij odpowiedzi, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Z której klasy pochodziła zwycięska drużyna?
Odpowiedź: Zwycięska drużyna jest z klasy 1.

2

, 2.

V a

, 3.

V b

, 4.

0

, 5.

3

, 6.

1

.Ile punktów średnio zdobył zawodnik zwycięskiej drużyny?
Odpowiedź: Zawodnik zwycięskiej drużyny zdobył średnio 1.

2

, 2.

V a

, 3.

V b

, 4.

0

, 5.

3

, 6.

1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 22

W poniższej tabeli podano średnie temperatury sześciu najbliższych Słońcu planet Układu Słonecznego.

Planeta	Średnia temperatura
Merkury	$350 ° C$
Wenus	$482 ° C$
Ziemia	$17 ° C$
Mars	$- 63 ° C$
Jowisz	$- 121 ° C$
Saturn	$- 125 ° C$

RyQb6Kig41x7A

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RyzU8Uq2DoFWO

Ćwiczenie 23

W konkursie matematycznym "Minusy wygrywają" uczeń za prawidłowo rozwiązane zadanie otrzymywał

(- 2)

punkty, za brak rozwiązania

(- 4)

punkty, a za błędną odpowiedź

(- 7)

punków. Uczniowie rozwiązywali

15

zadań. Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Marek rozwiązał poprawnie

11

zadań, na jedno nie udzielił odpowiedzi, a pozostałe rozwiązał błędnie. Marek zdobył łącznie Tu uzupełnij punktów. Dorota nie rozwiązała

2

zadań, na

3

udzieliła błędnej odpowiedzi, a pozostałe zadania rozwiązała poprawnie. Dorota zdobyła łącznie Tu uzupełnij punktów. Iza rozwiązała w sumie

13

zadań, z czego

9

było rozwiązanych poprawnie. Iza zdobyła łącznie Tu uzupełnij punkty.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 24

Na diagramie przedstawiono średnią temperaturę powietrza zanotowaną w ciągu jednego tygodnia stycznia.

Rxt7317AWJJx91

Diagram słupkowy ilustruje temperaturę powietrza, w stopniach Celsjusza, w ciągu jednego tygodnia. W poniedziałek temperatura wynosiła -4, we wtorek -1, w środę -2, w czwartek 3, w piątek -3, w sobotę 2, w niedzielę 5 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1drpLFjhIHTi

Wykorzystaj dane przedstawione na diagramie i odpowiedz na pytania. Uzupełnij odpowiedzi, wpisując w luki odpowiednie słowa lub liczby. W jakich dniach temperatura była niższa od

- 1

Celsjusza? Odpowiedź: Te dni tygodnia to Tu uzupełnij, Tu uzupełnij i Tu uzupełnij. O ile stopni temperatura w niedzielę była wyższa niż we wtorek? Odpowiedź: Temperatura w niedzielę była wyższa o Tu uzupełnij

° C

. Jaka była różnica między najwyższą i najniższą temperaturą w tym tygodniu? Odpowiedź: Różnica między tymi temperaturami wynosiła Tu uzupełnij

° C

. Jaka była średnia temperatura w ciągu czterech pierwszych dni tego tygodnia? Odpowiedź: Średnia temperatura w ciągu czterech pierwszych dni tego tygodnia wynosiła Tu uzupełnij

° C

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RGdydc1UE2PoM

Ćwiczenie 25

Mówimy, że dług rośnie, gdy liczba ujemna, która go określa maleje. Pan Wojtek zadłuża się na

24

euro miesięcznie. Uzupełnij poniższe zdania odpowiednimi liczbami. Kliknij w lukę, aby rozwinąć listę i wybierz odpowiednie liczby w każdym zdaniu. W styczniu stan konta pana Wojtka wynosił

0

euro.
Po

2

miesiącach dług pana Wojtka wynosił 1.

- 288

, 2.

- 144

, 3.

48

, 4.

- 48

, 5.

- 432

, 6.

108

euro, a jego stan konta 1.

- 288

, 2.

- 144

, 3.

48

, 4.

- 48

, 5.

- 432

, 6.

108

euro.
Po

6

miesiącach stan konta był równy 1.

- 288

, 2.

- 144

, 3.

48

, 4.

- 48

, 5.

- 432

, 6.

108

, a po roku 1.

- 288

, 2.

- 144

, 3.

48

, 4.

- 48

, 5.

- 432

, 6.

108

euro.
Po

18

miesiącach saldo konta pana Wojtka wynosiło 1.

- 288

, 2.

- 144

, 3.

48

, 4.

- 48

, 5.

- 432

, 6.

108

.
Pan Wojtek zamierza spłacić swój dług w

4

równych ratach po 1.

- 288

, 2.

- 144

, 3.

48

, 4.

- 48

, 5.

- 432

, 6.

108

euro.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 26

W finale szkolnego turnieju „Wiem wszystko” spotkali się: Jola, Andrzej i Łukasz. Za odpowiedź można było uzyskać punkty dodatnie lub ujemne. Wyniki pięciu rund podane są w poniższej tabeli.

Zawodnicy	Runda
Zawodnicy	$I$	$II$	$III$	$IV$	$V$	$I - V$
Jola	$- 8$	$6$	$5$	$- 10$	$5$
Andrzej	$2$	$- 5$	$- 4$	$6$	$- 3$
Łukasz	$7$	$- 2$	$5$	$- 4$	$7$

RAE54oCMx6Rh5

Oblicz, ile punktów zdobyli zawodnicy, a następnie uzupełnij poniższe zdania odpowiednimi wyrażeniami. Kliknij w lukę, aby rozwinąć listę i wybierz odpowiednie słowo lub liczbę w każdym zdaniu.

I

miejsce przypadło 1.

20

, 2. Andrzejowi, 3. Joli, 4. Łukaszowi, 5.

21

, 6.

17

, 7.

14

.Zawodnik, który zajął

I

miejsce, miał o 1.

20

, 2. Andrzejowi, 3. Joli, 4. Łukaszowi, 5.

21

, 6.

17

, 7.

14

punktów więcej niż zawodnik z

III

miejsca.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Słownik

liczby całkowite

to liczby naturalne dodatnie, liczby do nich przeciwne i liczba zero.

wartość bezwzględna

odległość liczby od zera na osi liczbowej.

liczby przeciwne

różne liczby, które mają takąość bezwzględną.

Notatnik

Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.

R1b8OvSPUG8s3

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

4. Działania na liczbach całkowitych

Działania na liczbach całkowitych