Podstawy fizyczne pneumatyki

bg‑turquoise

ATLAS INTERAKTYWNY

W pneumatyce wykorzystuje się tylko niektóre wielkości fizyczne, które są zawarte w międzynarodowym układzie jednostek miar, oznaczone krótko $SI$ (z fr. Systeme International). Będą one potrzebne do lepszego zrozumienia praw rządzących zachowaniem się powietrza. Należą do nich:

Wielkości podstawowe,
Tabela 1. Wielkości podstawowe
Wielkość
Oznaczenie
Jednostki
Długość
$l$
metr, $m$
Masa
$m$
kilogram, $k g$
Czas
$t$
sekunda, $s$
Temperatura
$T$
kelwin, $K$ $(0^{\circ} C) = 273, 15 K$

Tabela 1. Wielkości podstawowe
Wielkość	Oznaczenie	Jednostki
Długość	$l$	metr, $m$
Masa	$m$	kilogram, $k g$
Czas	$t$	sekunda, $s$
Temperatura	$T$	kelwin, $K$ $(0^{\circ} C) = 273, 15 K$

Wielkości pochodne.

Tabela 2. Wielkości pochodne
Wielkość	Oznaczenie	Jednostki
Siła	$F$	newton, $N$ $(1 N = 1 kg \cdot \frac{m}{s^{2}})$
Powierzchnia	$A$	metr kwadratowy, $m^{2}$
Objętość	$V$	metr sześcienny, $m^{3}$
Prędkość	$v$	metr na sekundę, $\frac{m}{s}$
Natężenie przepływu	$Q$	metr sześcienny na sekundę, $\frac{m^{3}}{s}$
Ciśnienie	$p$	pascal, $Pa$ $(1 Pa = 1 \frac{N}{m^{2}})$

Ciśnienie

Ciśnienie jest jednym z podstawowych parametrów opisujących stan powietrza. Zgodnie z prawem Pascala $1 Pa$ odpowiada ciśnieniu, które wywiera prostopadle działająca siła $1 N$ na powierzchnię $1 m^{2}$ .

P = \frac{F}{A} [Pa = \frac{N}{m^{2}}]

Wartość mierzonego ciśnienia zależy od przyjętego poziomu odniesienia. Ciśnienie zmierzone względem próżni $(0 Pa)$ jest nazywane ciśnieniem absolutnym $p_{a b s}$ lub bezwzględnym. Ciśnienie wywierane przez słup powietrza atmosferycznego nosi nazwę ciśnienia barometrycznego (atmosferycznego) $p_{a t m}$ .

Ciśnienie manometryczne $p$ (ciśnienie względne) jest to różnica ciśnienia absolutnego i ciśnienia otoczenia, którym najczęściej jest ciśnienie atmosferyczne, wskazywane przez barometr. Ciśnienie manometryczne może przyjmować wartości większe od zera i wówczas mówi się o nadciśnieniu lub wartości mniejsze od zera i wówczas mówi się o podciśnieniu. Rodzaje ciśnień wyjaśnia poniższy rysunek.

p_{a b s} = p_{a t m} \pm p

Rh6NFnHkuvQD9

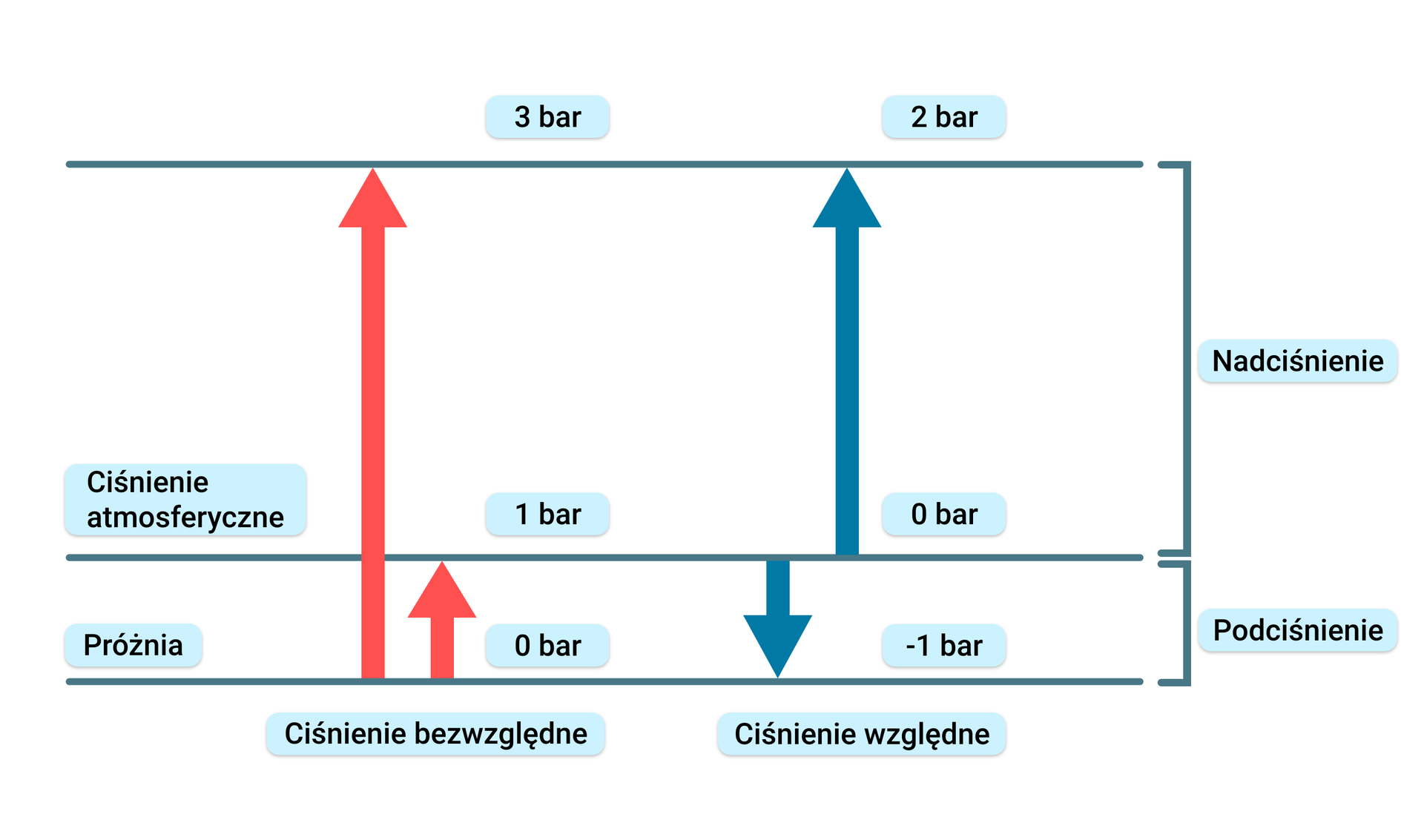
Rodzaje ciśnień
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Tabela 3. Obliczanie ciśnienia absolutnego
Przykład 1
Manometr wskazuje ciśnienie $6 bar$ . Ile wynosi ciśnienie absolutne? Odpowiedź Ciśnienie absolutne jest sumą ciśnienia atmosferycznego $(1 bar)$ i nadciśnienia $(+ 6 bar)$ , więc: $p_{a b s} = p_{a t m} \pm p = 1 bar + 6 bar = 7 bar$

Tabela 4. Obliczanie ciśnienia absolutnego
Przykład 2
Wakuometr wskazuje ciśnienie $80 kPa$ . Ile wynosi ciśnienie absolutne? Odpowiedź Ciśnienie absolutne jest różnicą ciśnienia atmosferycznego $(1 bar = 100 kPa)$ i podciśnienia $(- 80 kPa)$ , więc: $p_{a b s} = p_{a t m} \pm p = 100 kPa - 80 kPa = 20 kPa$

Przyrządy do pomiaru ciśnień

barometr – pomiar ciśnienia atmosferycznego,
manometr – pomiar nadciśnienia,
wakuometr – pomiar podciśnienia.

Jednostki ciśnienia

Jednostką obowiązującą ciśnienia zgodnie z układem $SI$ jest Pascal $(Pa)$ i jego wielokrotności.

$1 Pa = 1 \frac{N}{m^{2}}$ ,
$1 MPa = 1 \frac{N}{{mm}^{2}}$ ,
$1 MPa = 1000 kPa = 10000 hPa$ .

Ciśnienia podawane są także w innych jednostkach. Obowiązującą i szeroko stosowaną w pneumatyce są bary $(bar)$

$1 bar = 10^{5} Pa = 1000 hPa = 100 kPa = 0, 1 MPa$ .

Można jeszcze spotkać stare jednostki, od których już się odchodzi, m.in.:

atmosfera techniczna (ciśnienie wywierane przez $10000 mm$ słupa wody)
- $1 at = 10000 {mmH}_{2} O = 98066, 5 Pa$
atmosfera fizyczna (ciśnienie wywierane przez $760 mm$ słupa rtęci)
- $1 atm = 760 mmHg = 101325 Pa$

Dla praktyki warsztatowej całkowicie wystarczające jest następujące przybliżenie:

$1 at \approx 1 atm \approx 100000 Pa \approx 1 bar$

Tabela 5. Zamiana jednostek
Przykład
Zamień $20 mbar$ na $hPa$ . Odpowiedź Przedrostek mili $(m)$ to $10^{- 3}$ , przedrostek hekto $(h)$ to $10^{2}$ , a $1 bar = 10^{5} Pa$ , zatem: $20 mbar = 20 \cdot 10^{- 3} \cdot 10^{5} Pa = 20 \cdot 10^{2} Pa = 20 hPa$

Ogólne równanie stanu gazu

Stan fizyczny powietrza w zamkniętym zbiorniku (stała niezmienna ilość powietrza) określają trzy parametry:

$p$ – ciśnienie gazu, $Pa$
$V$ – objętość gazu, $m^{3}$
$T$ – temperatura gazu, $K$

W wyniku badań i doświadczeń odkryto, sprawdzono i ujęto w matematyczną zależność związek między tymi trzema parametrami, który nosi nazwę równania stanu gazu (równanie Clapeyron’a):

\frac{p_{1} \cdot V_{1}}{T_{1}} = \frac{p_{2} \cdot V_{2}}{T_{2}} = const

Przy skończonej ilości gazu iloczyn ciśnienia i objętości podzielony przez temperaturę absolutną jest stały. Z tego ogólnego równania stanu gazu otrzymuje się przemiany stanu gazu, jeśli aktualnie jeden z trzech czynników $p$ , $V$ lub $T$ pozostaje stały. Jeżeli objętość $V$ jest stała, to mamy do czynienia z przemianą izochoryczną. Jeżeli ciśnienie $p$ jest stałe to jest to przemiana izobaryczna. Natomiast, gdy temperatura $T$ się nie zmienia to zachodzi przemiana izotermiczna.

Przemiana izochoryczna $(V = const)$

Przemiana izochoryczna to proces, w którym objętość gazu jest niezmienna $(V = const)$ , a pozostałe parametry ulegają zmianie. Ogrzewając gaz w pojemniku, czyli zwiększając jego temperaturę, w wyniku takiego działania, nastąpi wzrost ciśnienia gazu. W momencie ochładzania gazu, ciśnienie będzie malało.

RnQUPJoIfsbRk

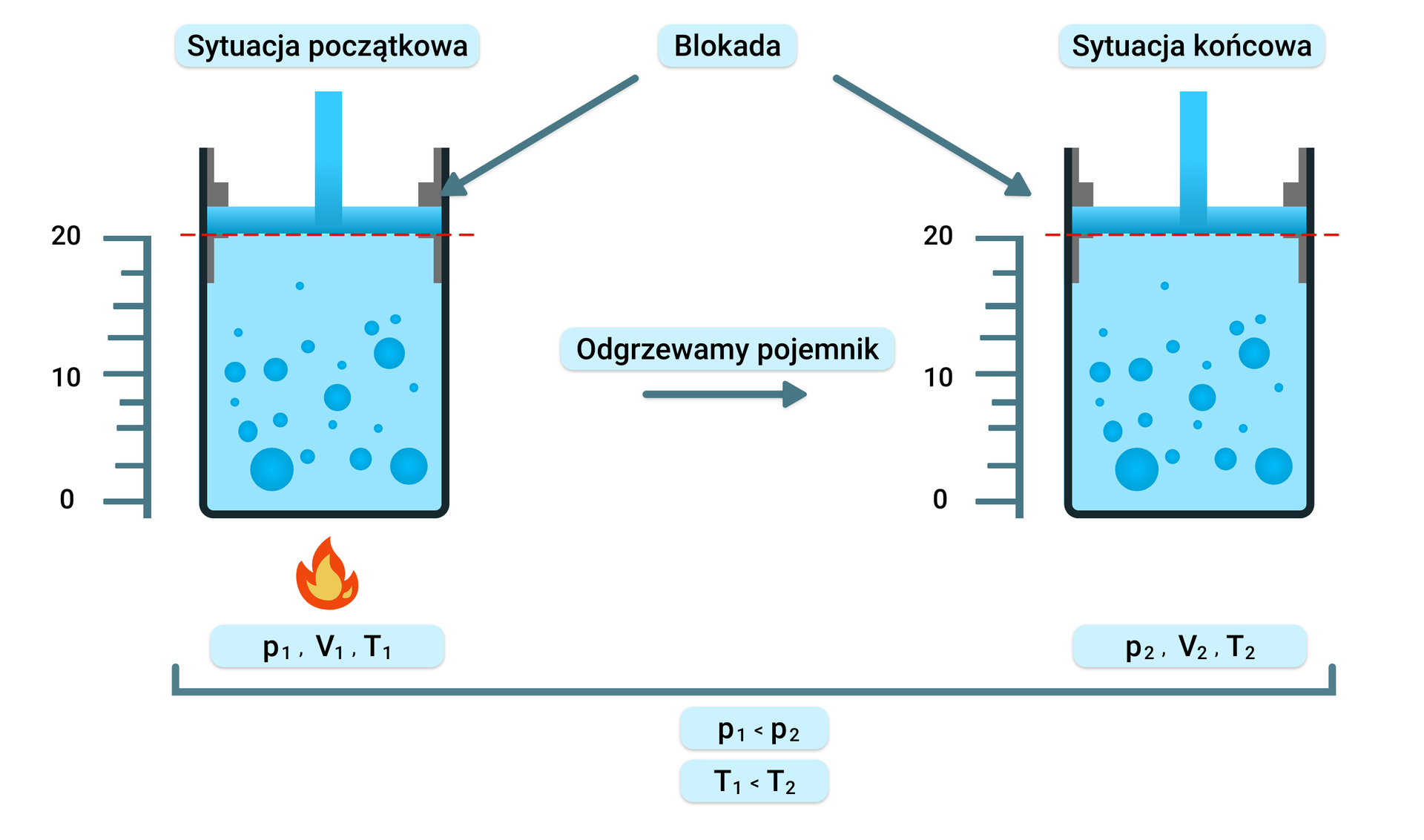
Grafika przedstawiająca istotę przemiany izochorycznej
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Równanie Clapeyrona w tym procesie przyjmuje następującą postać:

\frac{p_{1} \cdot V_{1}}{T_{1}} = \frac{p_{2} \cdot V_{1}}{T_{2}}

Dzieląc powyższe równanie przez $V_{1}$ , otrzymamy:

\frac{p_{1}}{T_{1}} = \frac{p_{2}}{T_{2}} \leftrightarrow \frac{p_{1}}{p_{2}} = \frac{T_{1}}{T_{2}} = const

Przemianę izochoryczną opisuje prawo Charlesa: W izochorycznej przemianie stałej masy gazu ciśnienie panujące w gazie jest wprost proporcjonalne do jego temperatury.

R6iZhM71bc7xO

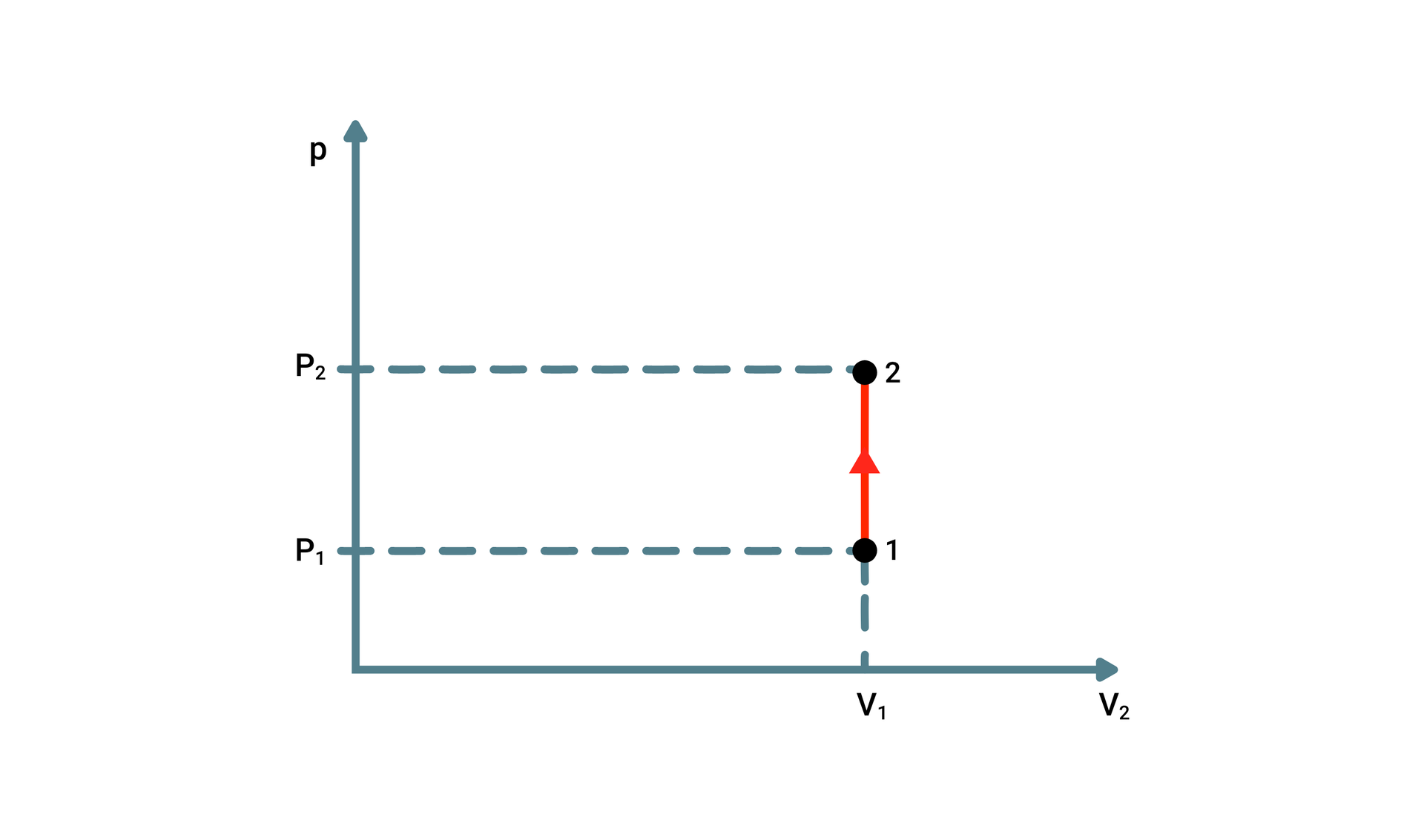
Wykres pV dla przemiany izochorycznej — Wykres $p (V)$ dla przemiany izochorycznej
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Przemianę izochoryczną można zaobserwować, gdy pozostawione na nasłonecznionym obszarze opony samochodowe, zaczynają się nagrzewać, w skutek czego ciśnienie w nich rośnie. Podobnie jest z nadmuchanym w gorący dzień materacem. Po wrzuceniu do zimnej wody robi się miękki i wiotki w wyniku obniżenia w nim ciśnienia.

Tabela 6. Przemiana izochoryczna
Przykład
Ciśnienie powietrza w zamkniętym pojemniku o temperaturze $20 ° C$ jest pod ciśnieniem absolutnym $1 bara$ . O ile wzrośnie ciśnienie gazu w pojemniku, jeżeli podgrzejemy go do temperatury $300 ° C$ ? Odpowiedź W celu wyliczenia ciśnienia powietrza w zamkniętym pojemniku korzystamy z zależności wynikającej z przemiany izochorycznej. Trzeba jednak zamienić temperaturę wyrażoną w $° C$ na temperaturę bezwzględną wyrażoną w kelwinach $(K)$ : $T_{1} = 20 ° C + 273 = 293 K,$ $T_{2} = 300 ° C + 273 = 573 K,$ Obliczamy ciśnienie panujące w zbiorniku dla wyższej temperatury: $\frac{p_{1}}{T_{1}} = \frac{p_{2}}{T_{2}} \leftrightarrow p_{2} = p_{1} \cdot \frac{T_{2}}{T_{1}} = 1 bar \cdot \frac{573 K}{293 K} = 1, 95 bar$ Ciśnienie wzrośnie zatem o: $∆ p = p_{2} - p_{1} = 1, 95 bar - 1 bar = 0, 95 bar$

Przemiana izobaryczna $(p = const)$

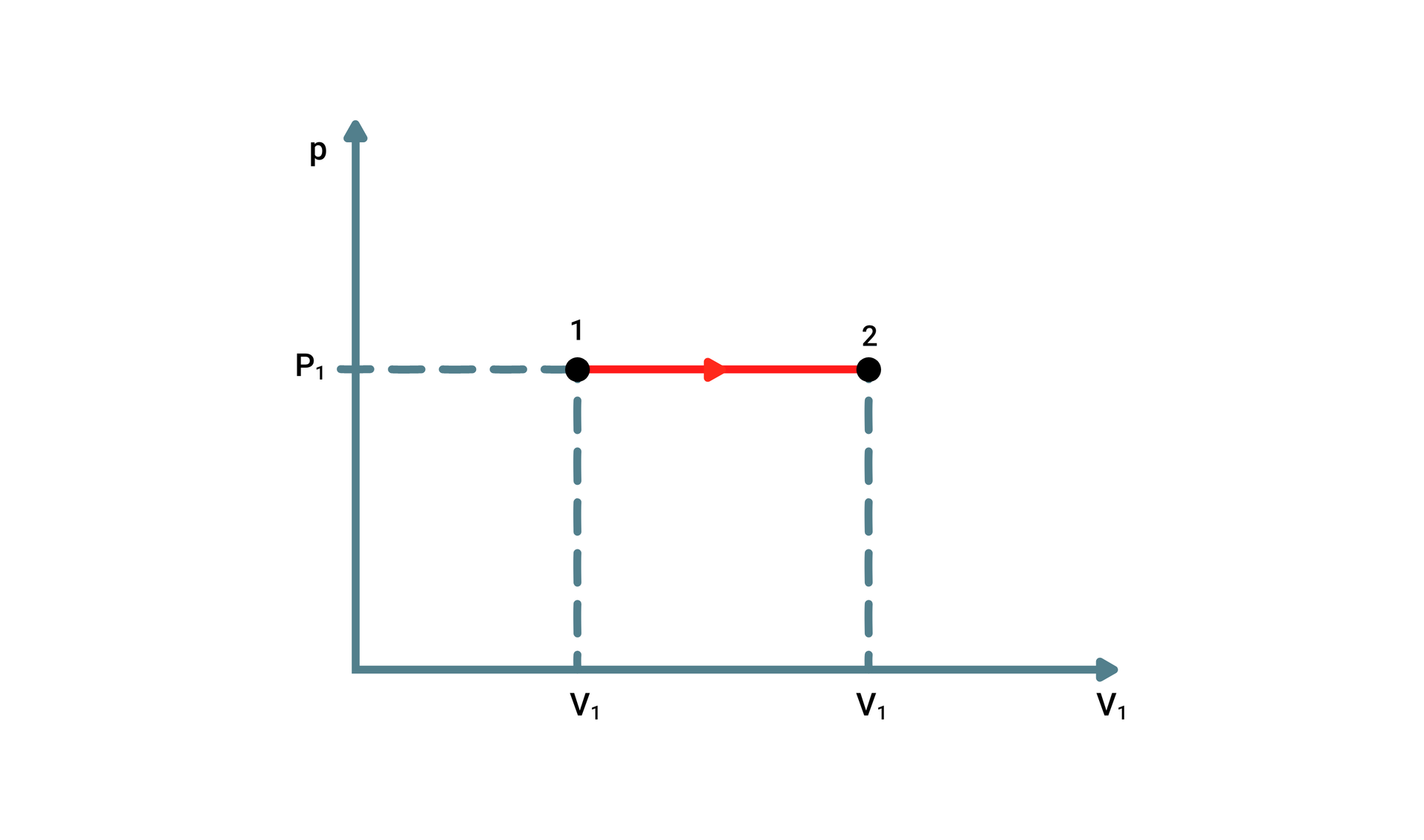
Przemiana izobaryczna zakłada, że ciśnienie gazu jest stałe $(p = const)$ , a pozostałe wielkości ulegają zmianie. Ogrzewając gaz zamknięty w pojemniku z tłokiem, który nie jest zablokowany i może się poruszać swobodnie góra‑dół (pomijając tarcie pomiędzy tłokiem, a ściankami pojemnika), można zauważyć, że wraz ze wzrostem temperatury następuje wzrost objętości gazu (tłok porusza się do góry). W chwili gdy następuje oziębienie pojemnika i temperatura obniża się – objętość gazu maleje, a tłok opada w dół.

R1QP8F6hIWCTA

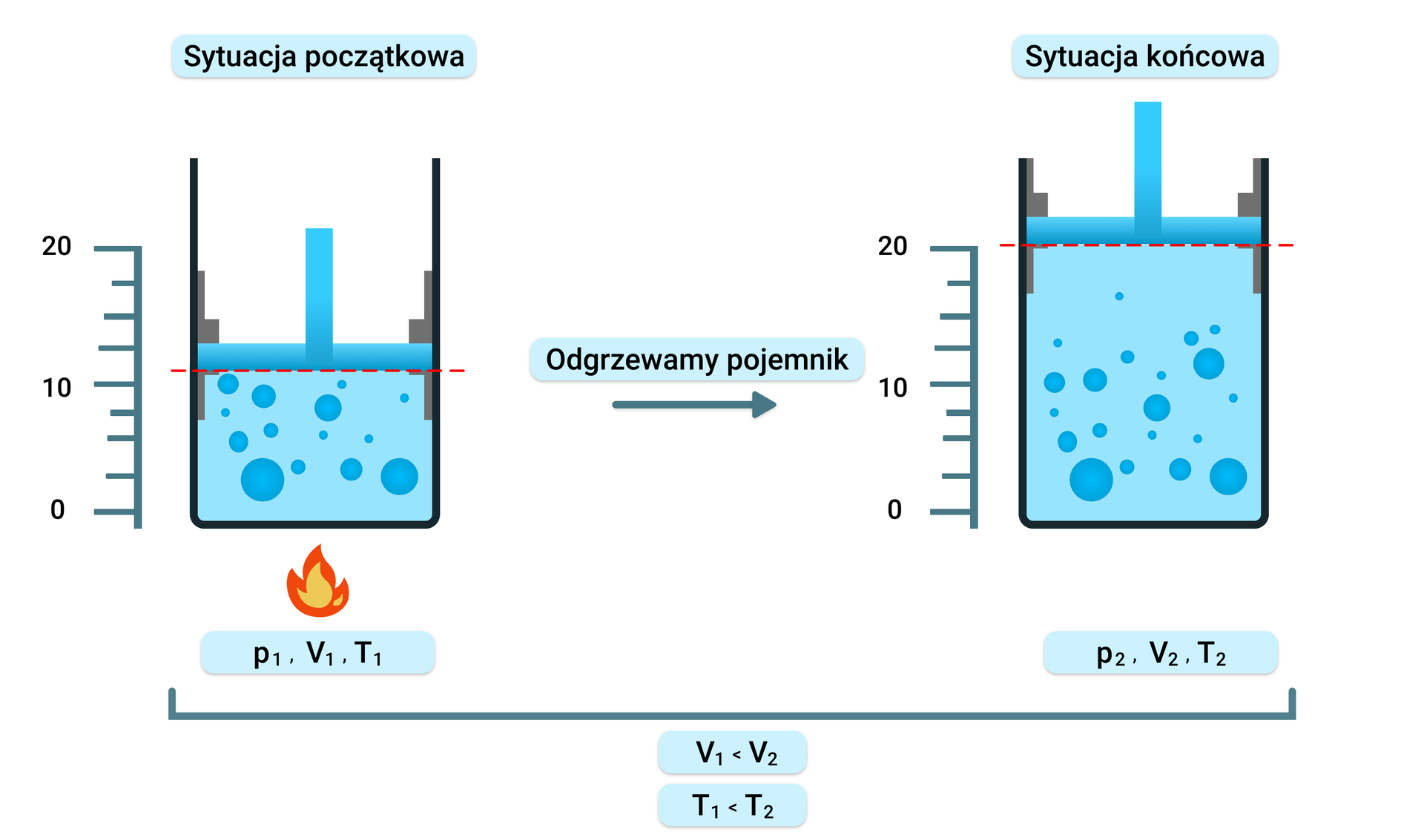
Grafika przedstawiająca istotę przemiany izobarycznej
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Równanie Clapeyrona w tym procesie przyjmuje następującą postać:

\frac{p_{1} \cdot V_{1}}{T_{1}} = \frac{p_{1} \cdot V_{2}}{T_{2}}

Dzieląc powyższe równanie przez $p_{1}$ , otrzymamy:

\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}} \leftrightarrow \frac{V_{1}}{V_{2}} = \frac{T_{1}}{T_{2}} = const

Przemianę izobaryczną opisuje prawo Gay‑Lussaca: W izobarycznej przemianie stałej masy gazu objętość zajmowana przez gaz jest wprost proporcjonalna do jego temperatury.

RtjXPz40v7QFJ

Wykres pV dla przemiany izobarycznej — Wykres $p (V)$ dla przemiany izobarycznej
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Przemiana izotermiczna $(T = const)$

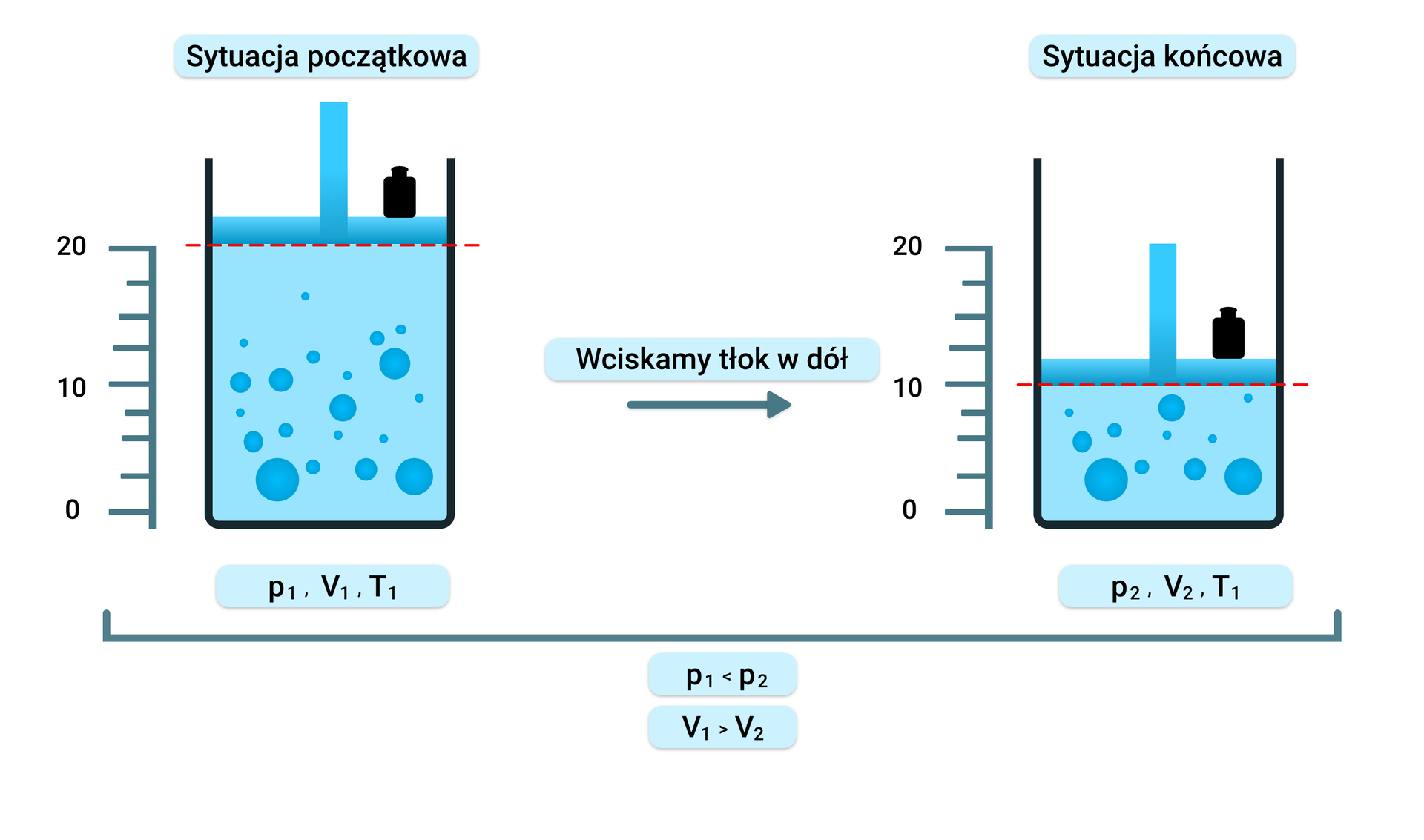
Przemiana izotermiczna charakteryzuje się tym, że temperatura gazu jest stała $(T = const)$ , a zmianie ulegają ciśnienie i objętość. Mając pojemnik z gazem, ustalamy kolejno parametry $p_{1}$ , $V_{1}$ , $T_{1}$ . Następnie wykonując pracę poprzez wciskanie tłoka w dół, objętość gazu się zmniejsza, a w skutek tego ciśnienie się zwiększa. Pamiętając oczywiście, że temperatura $T_{1}$ jest niezmienna (szybka wymiana ciepła z otoczeniem).

R1cNavlHnnES5

Grafika przedstawiająca istotę przemiany izotermicznej
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Równanie Clapeyrona w tym procesie przyjmuje następującą postać:

\frac{p_{1} \cdot V_{1}}{T_{1}} = \frac{p_{2} \cdot V_{2}}{T_{1}}

Mnożąc powyższe równanie przez $T_{1}$ , otrzymamy:

p_{1} \cdot V_{1} = p_{2} \cdot V_{2}

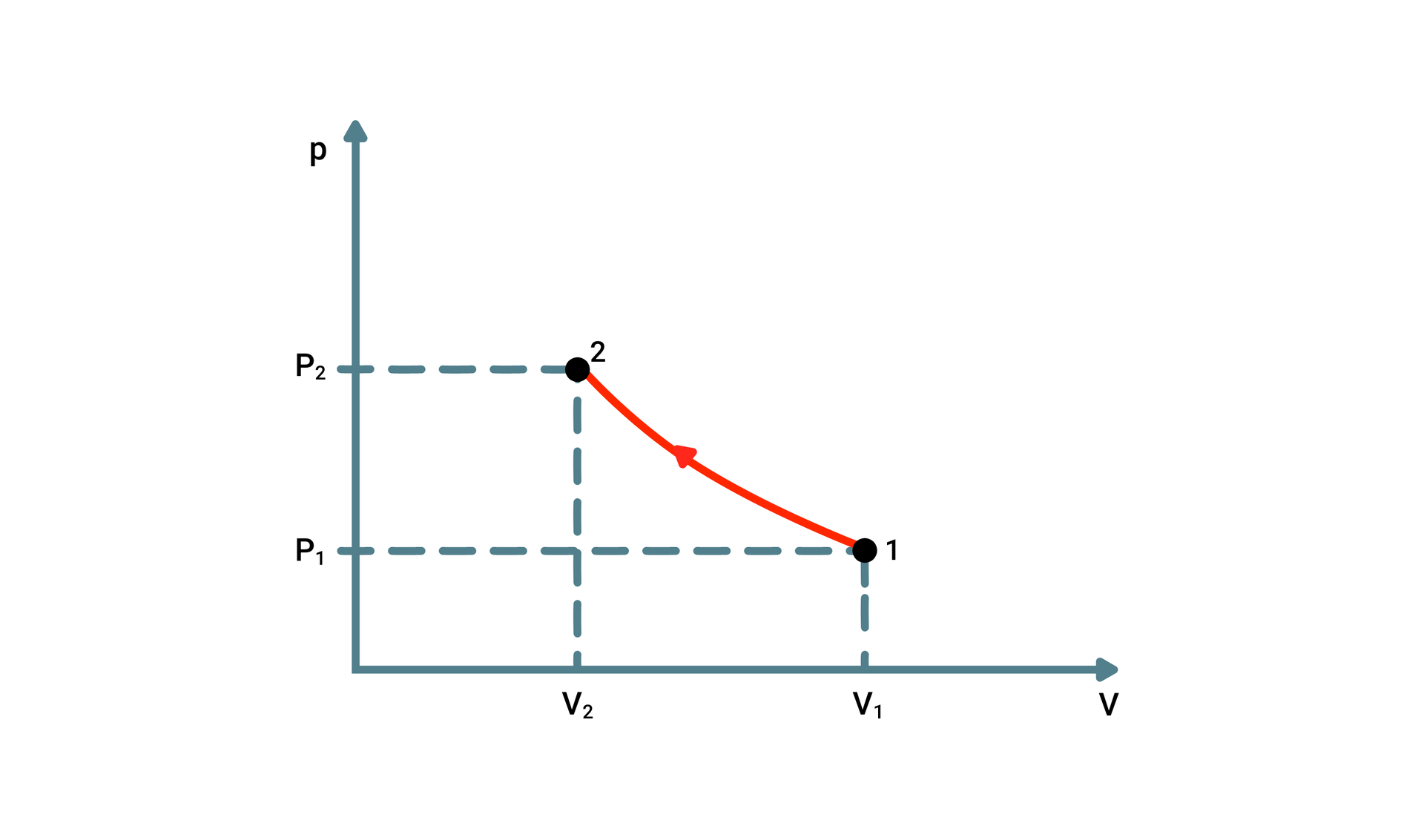
Przemianę izotermiczną opisuje prawo Boyle’a‑Mariotte’a: W izotermicznej przemianie stałej masy gazu ciśnienie, panujące w gazie, jest odwrotnie proporcjonalne do jego objętości.

R15pVwRkNJgcy

Wykres pV dla przemiany izotermicznej — Wykres $p (V)$ dla przemiany izotermicznej
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Tabela 7. Przemiana izotermiczna
Przykład
W zamkniętym zbiorniku z ruchomym tłokiem o objętości $V_{1} = 2 m^{3}$ znajduje się gaz pod ciśnieniem $p_{1} = 3 bar$ . Ile wyniesie ciśnienie gazu w zbiorniku, jeśli poprzez przesunięcie tłoka zmniejszymy objętość zbiornika o $800$ litrów? Zakładamy, że temperatura gazu nie uległa zmianie podczas sprężania. Odpowiedź Najpierw należy przeliczyć jednostki objętości na takie same, np. na litry. $1 m^{3}$ to $1000 {dm}^{3}$ , a $1 {dm}^{3}$ to $1 l$ (litr). Zatem $2 m^{3} = 2000 l$ . Teraz należy określić objętość zbiornika $V_{2}$ po przemieszczeniu tłoka. Wyniesie ona $V_{2} = 2000 l - 800 l = 1200 l$ . Teraz wystarczy wszystkie dane podstawić do wzoru na przemianę izotermiczną i wyliczyć ciśnienie $p_{2}$ . $p_{1} \cdot V_{1} = p_{2} \cdot V_{2} \Rightarrow p_{2} = p_{1} \cdot \frac{V_{1}}{V_{2}}$ $p_{2} = 3 bar \cdot \frac{2000 l}{1200 l} = 5 bar$

Przepływ gazu

Rozróżnia się dwa rodzaje przepływów płynu:

Przepływ laminarny (warstwowy) - przepływ, w którym płyn przepływa w równoległych warstwach, bez zakłóceń między warstwami (mieszania się). Przepływ tego typu występuje przy odpowiednio małych prędkościach przepływu.
R1DLSncj2SFvK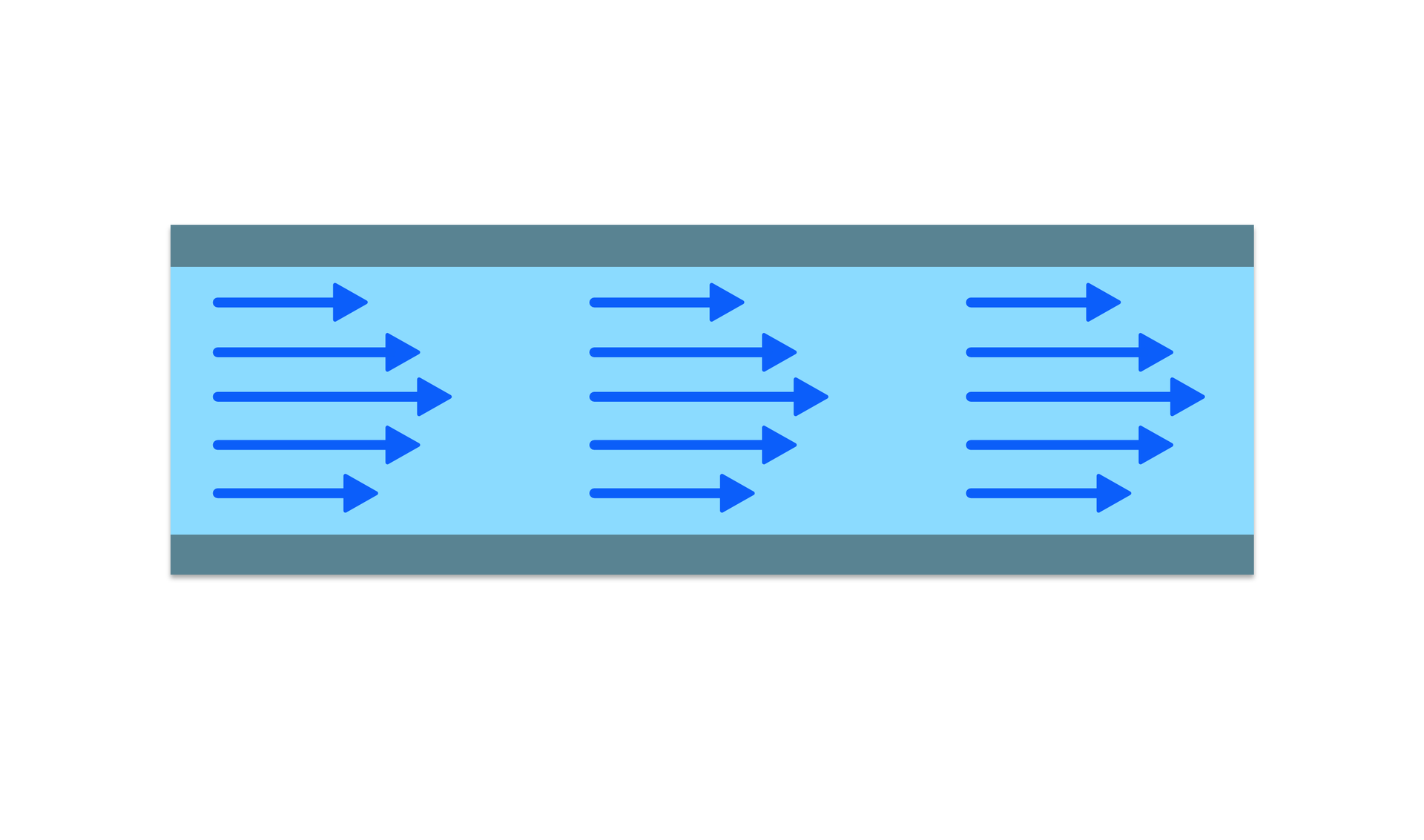
Równoległe linie prądu gazu podczas przepływu laminarnego
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.
Przepływ turbulentny (wirowy lub burzliwy) - tory cząstek stają się chaotyczne, nie mają ustalonych linii ani strug prądu. Ruch płynu odbywa się z silnymi zawirowaniami. Przy przepływie turbulentnym występuje mieszanie się poszczególnych warstw.
RPXjyWRmhYNYE
Chaotyczne linie prądu gazu w przepływie turbulentnym
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Parametrem określającym przepływ w przewodzie jest natężenie przepływu $Q$ . Zwane jest również objętościowym strumieniem objętości. Wylicza się je jako stosunek objętości przepływającego gazu w przewodzie $V (m^{3})$ do czasu jego przepływu $t (s)$ . Zatem jednostką objętościowego natężenia przepływu jest $\frac{m^{3}}{s}$ .

Q = \frac{V}{t}

Jeżeli za objętość podstawimy iloczyn przekroju przewodu $A (m^{2})$ i długość przewodu zajmowanego przez gaz $l (m)$ , to możemy powyższe równanie przekształcić do postaci:

Q = \frac{V}{t} = \frac{A \cdot l}{t} = A \cdot \frac{l}{t} = A \cdot v

gdzie:

$A$ – powierzchnia przekroju poprzecznego przewodu, $m^{2}$
$v$ – prędkość gazu, $\frac{m}{s}$

Prawo ciągłości strugi

Jeżeli założyć, że dla gazu nieściśliwego temperatura jest stała i jednakowa dla każdego przekroju przewodu i przepływ gazu jest laminarny, to objętość $V$ gazu wpływającego i odpływającego w ciągu jednej sekundy z dowolnego przekroju przewodu jest stała. Opisuje to następująca zależność:

Q = A_{1} \cdot v_{1} = A_{2} \cdot v_{2} = const

Prawo ciągłości strugi przedstawiono graficznie na poniższym rysunku.

Rsnv7oILZXNc0

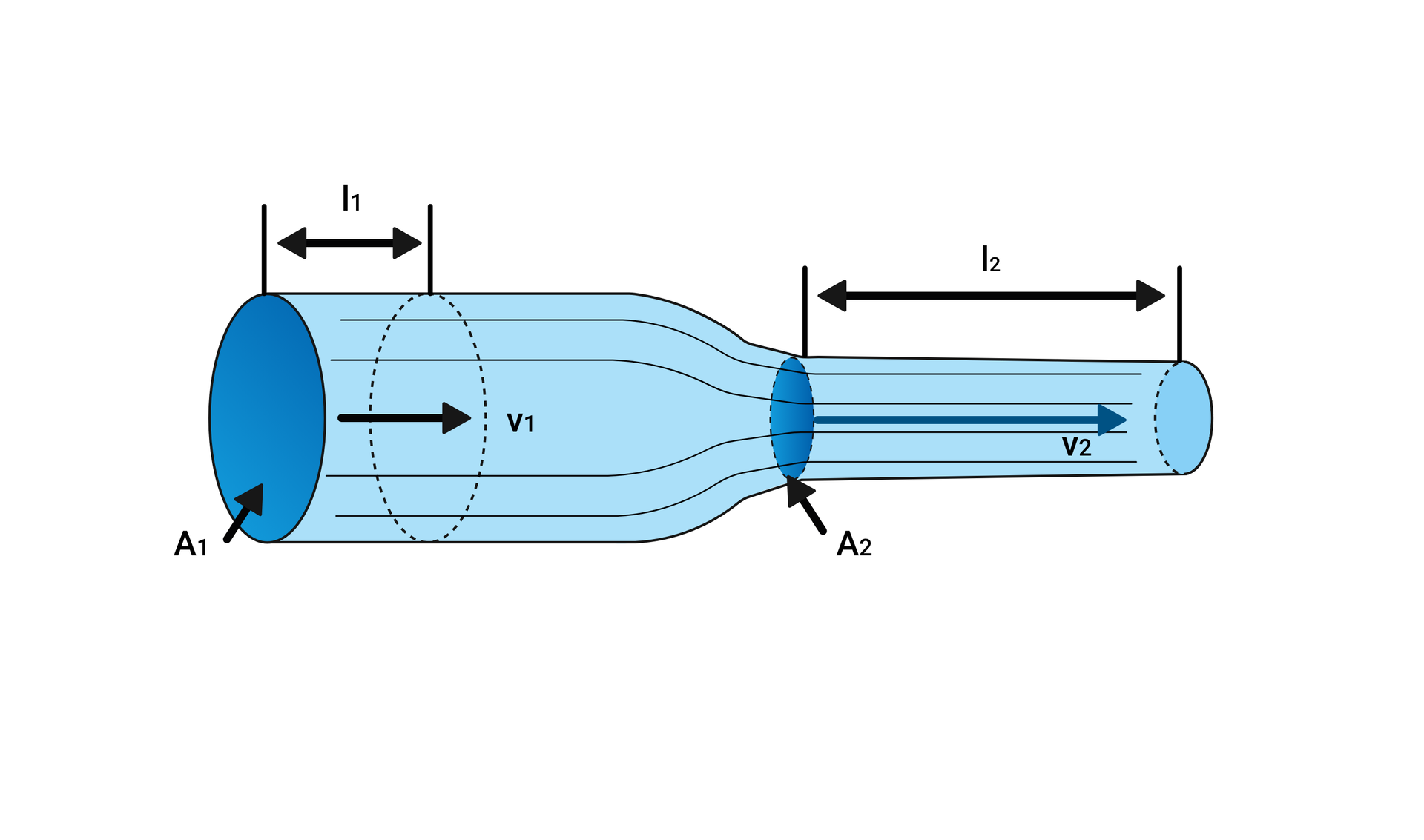
Graficzna interpretacja prawa ciągłości strugi
Źródło: Englishsquare.pl Sp. z o.o., licencja: CC BY-SA 3.0.

Z prawa ciągłości strugi wynika, że prędkość gazu jest odwrotnie proporcjonalna do przekroju poprzecznego przewodu. Jeśli przekrój przewodu zmniejszy się, np. trzykrotnie, to prędkość gazu w tym przewodzie zwiększy się trzykrotnie.

Tabela 8. Prawo ciągłości strugi
Przykład
Określ, jak zmieni się prędkość gazu w przewodzie, jeśli jego średnica wzrośnie dwukrotnie. Odpowiedź Jeżeli założymy, że w przewodzie o średnicy $d_{1}$ , gaz porusza się z prędkością $v_{1}$ , natomiast w przewodzie o średnicy $v_{2}$ z prędkością $d_{1}$ , to można zapisać równanie ciągłości strugi: $A_{1} \cdot v_{1} = A_{2} \cdot v_{2}$ Oczywiście, we wzorze występują przekroje poprzeczne przewodów, ale wiemy, że pole przekroju kołowego wynosi: $A = π \cdot \frac{d^{2}}{4}$ . Zatem podstawiając do wzoru otrzymujemy: $\frac{π {d_{1}}^{2}}{4} \cdot v_{1} = \frac{π {d_{2}}^{2}}{4} \cdot v_{2}$ Po przekształceniu wzoru i wyliczeniu $v_{2}$ otrzymamy: $v_{2} = \frac{{d_{1}}^{2}}{{d_{2}}^{2}} \cdot v_{1} = {(\frac{d_{1}}{d_{2}})}^{2} \cdot v_{1} = {(\frac{1}{2})}^{2} \cdot v_{1} = \frac{1}{4} \cdot v_{1}$ Jak widać prędkość w przewodzie o średnicy dwukrotnie większej zmaleje czterokrotnie.

Powrót do spisu treściD1HeIWIJkPowrót do spisu treści

Wstęp

Właściwości powietrza