Symetrie
3. Figury osiowosymetryczne
Według Słownika Języka Polskiego PWN symetria to podzielność przedmiotu na odpowiadające sobie jednakowe lub analogiczne części, będące swym zwierciadlanym odbiciem albo pokrywające się po obrocie wokół punktu lub prostej
albo inaczej „równowaga i zgodność między poszczególnymi elementami jakiejś całości”.
Pojęcie symetrii znane jest od czasów starożytnych. Symetryczne są różne obiekty w przyrodzie oraz arcydzieła architektury i sztuki.





W tym materiale zawarte są informacje na temat figur osiowosymetrycznych. Podana jest definicja oraz niektóre własności tych figur. Zamieszczone tu przykłady pokazują sposoby rozwiązywania zadań związanych z tym tematem.
Film dostępny pod adresem /preview/resource/R1TGWWwaLUxxM
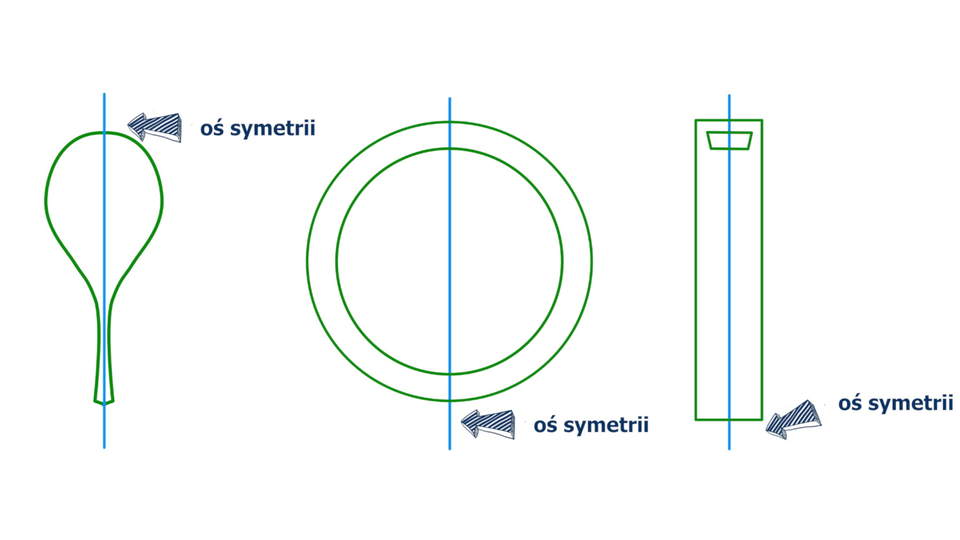
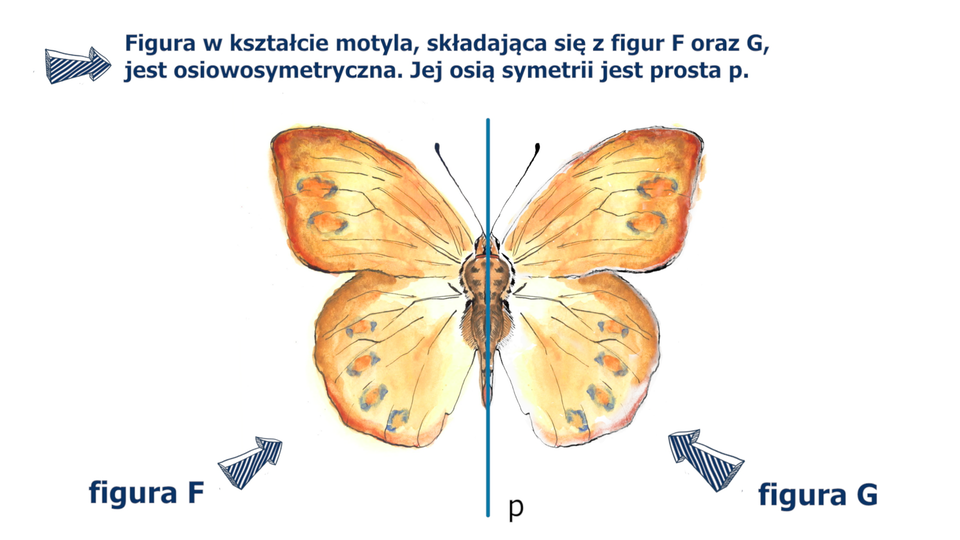
Animacja przedstawia przykłady figur osiowosymetrycznych.
Figura jest obrazem figury w symetrii względem prostej . Przesuwając suwak możemy połączyć figury i , otrzymując figurę w kształcie gitary.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dz2uyl9hl
W symetrii względem prostej punkty figury , które należały do figury , można przekształcić na odpowiednie punkty figury . Zatem każdy punkt figury można przekształcić w symetrii względem prostej na punkt należący również do figury . O takiej figurze mówimy, że jest osiowosymetryczna.
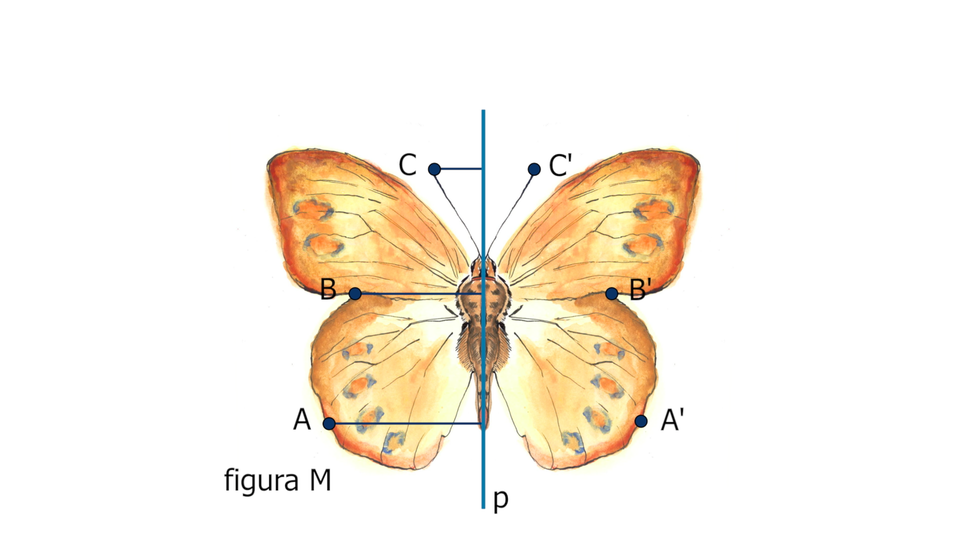
Weźmy trzy dowolne punkty , , i znajdźmy obrazy , , tych punktów w symetrii względem prostej .
Film dostępny pod adresem /preview/resource/R82DHdqBrCbzY
Animacja przedstawia jakie figury możemy nazywać figurami osiowosymetrycznymi.
Figurę nazywamy osiowosymetryczną, jeżeli istnieje taka prosta , iż każdy punkt figury , po przekształceniu w symetrii względem prostej , należy do figury .
Prostą nazywamy osią symetrii figury .
Przykłady figur osiowosymetrycznych

Figura osiowosymetryczna jest swoim obrazem w symetrii osiowej.
Przykłady czworokątów osiowosymetrycznych.


Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dz2uyl9hl
Odpowiedź:
W ten sposób możemy otrzymać różne trapezy równoramienne, deltoidy oraz trójkąty równoramienne.
Wskaż w najbliższym otoczeniu elementy, które można przyjąć za modele figur osiowosymetrycznych.
Obiekty, które przedstawiono na rysunkach w przykładowej odpowiedzi do ćwiczenia można uznać za figury osiowosymetryczne, ale w rzeczywistości są one bryłami.
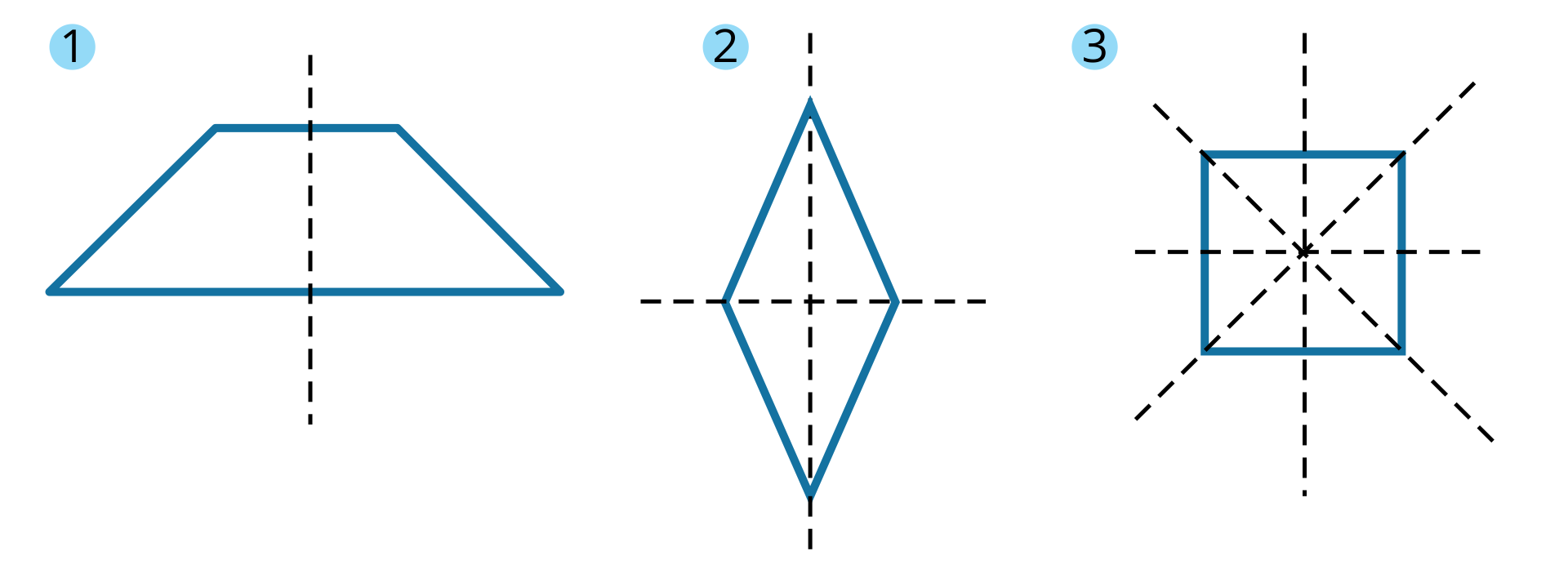
Przyjrzyjmy się wielokątom na rysunku. Ile osi symetrii ma każdy z nich?

Rozwiązanie:
Trójkąt równoboczny ma osie symetrii, a kwadrat ma osie symetrii.
Każdy z narysowanych wielokątów ma osie symetrii. Wskaż je.
Każdy z narysowanych wielokątów ma osie symetrii. Wskaż je. Podaj ile osi symetrii ma każda z nich.

Przykłady figur, które nie mają osi symetrii.

Płatki śniegu mają przepiękne kształty. Być może dlatego, że zawsze posiadają aż sześć osi symetrii. Ponadto każdy płatek jest wyjątkowy. Nie ma dwóch identycznych.

Figury osiowosymetryczne można otrzymać, wykorzystując symetrię względem prostej.
Film dostępny pod adresem /preview/resource/Rk7zzHRxMz8Vu
Animacja

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dz2uyl9hl
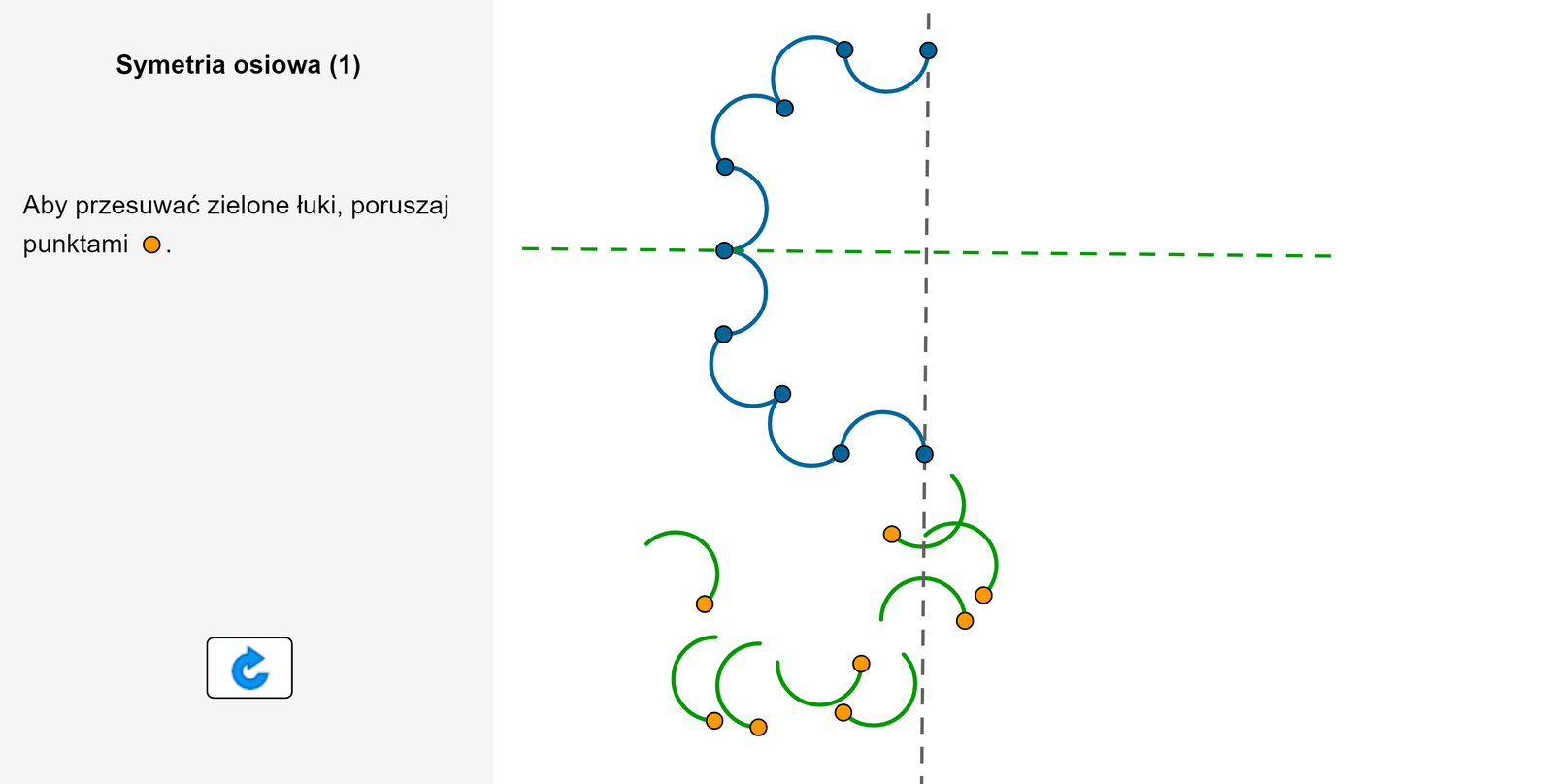
Figura w kolorze niebieskim, umieszczona na rysunku, jest osiowosymetryczna względem prostej w kolorze zielonym. Utwórz z zielonych łuków figurę symetryczną do początkowej względem prostej w kolorze szarym.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dz2uyl9hl
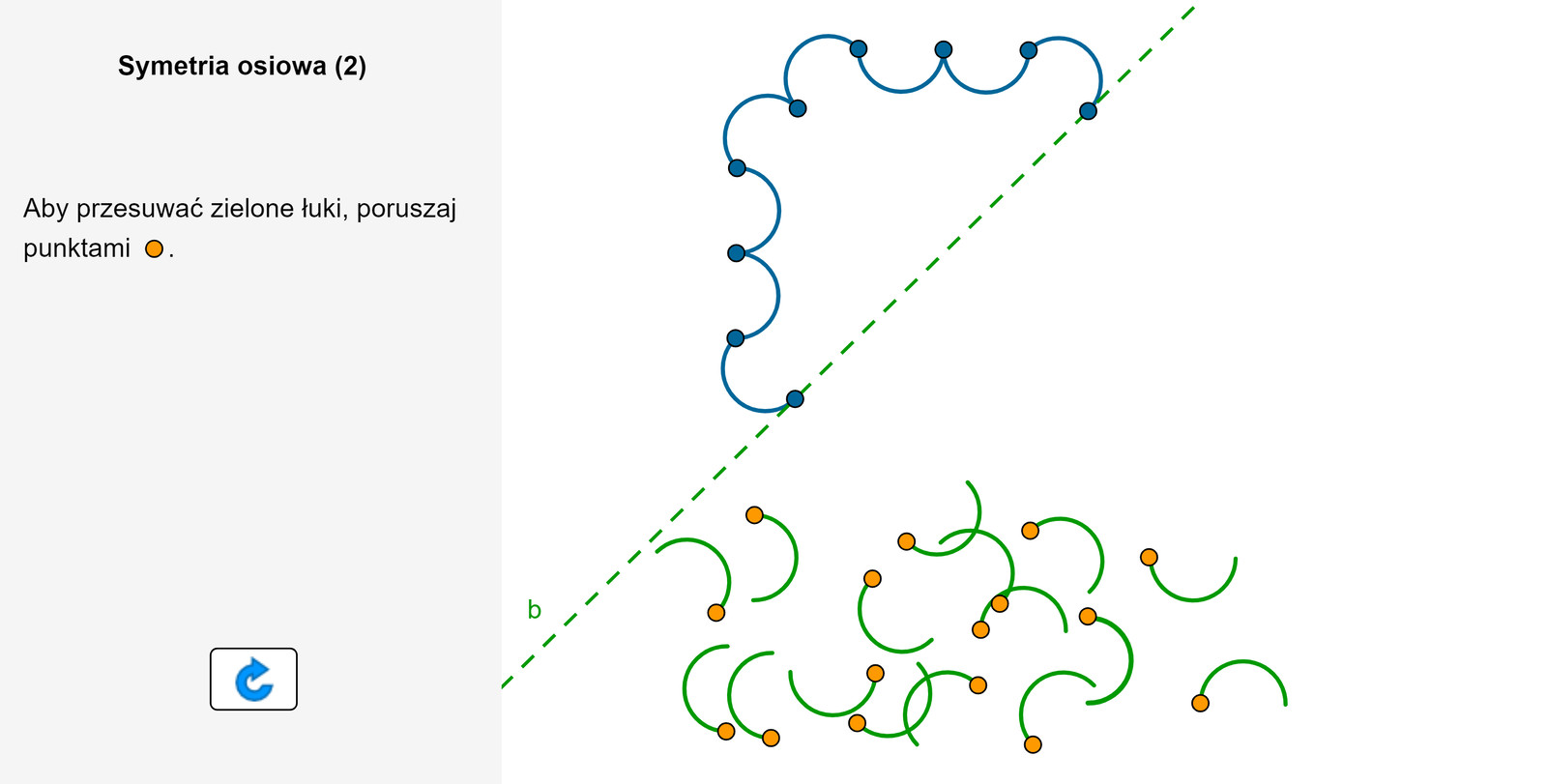
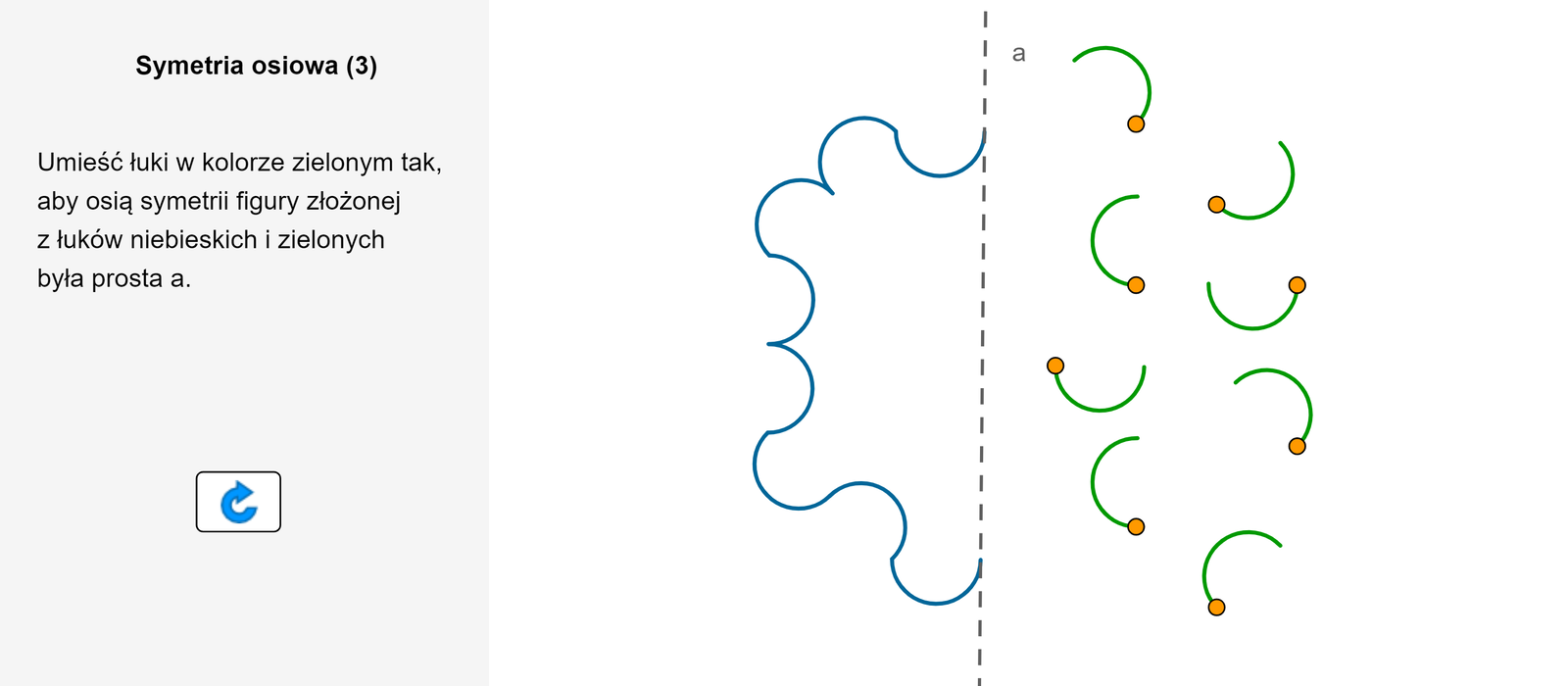
Ułóż zielone łuki tak, aby figura na rysunku była osiowosymetrycna.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dz2uyl9hl
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dz2uyl9hl
Odpowiedź: Odcinek ma 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery osie symetrii, mają one 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery punkt wspólny
Ile osi symetrii ma okrąg? Czy mają one punkt wspólny?
Odpowiedź: Okrąg ma 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery osi symetrii. Ich punktem wspólnym jest 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery.
Czy kwadrat ma osie symetrii?
Odpowiedź: Kwadrat ma 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery osie symetrii.
Czy każdy wielokąt ma oś symetrii?
Odpowiedź: Nie każdy wielokąt ma oś symetrii, np. 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery nie ma osi symetrii.
Czy prosta jest figurą osiowosymetryczną?
Odpowiedź: 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery, prosta 1. nieskończenie wiele, 2. jeden, 3. Tak, 4. punkt leżący na krawędzi okręgu, 5. trzy, 6. nie ma, 7. równoległobok (o ile nie jest rombem) o różnych przekątnych, 8. ma, 9. Nie, 10. środek okręgu, 11. dwanaście, 12. dwie, 13. cztery nieskończenie wiele osi symetrii.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/Dz2uyl9hl
Poszukaj figur osiowo symetrycznych wśród dużych drukowanych liter alfabetu łacińskiego.
Które z tych liter mają oś symetrii?
Czy są wśród tych liter takie, które mają więcej niż jedną oś symetrii?

Narysuj czworokąt, który ma
jedną oś symetrii,
dwie osie symetrii,
cztery osie symetrii.
Podaj czworokąt, który ma
jedną oś symetrii,
dwie osie symetrii,
cztery osie symetrii.
Wśród figur przedstawionych na rysunku wskaż figury osiowosymetryczne.

- OKO
- OTO
- KOT
- TOK
Przeciągnij w luki odpowiednie litery lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 1. , 2. , 3. , 4. 1. , 2. , 3. , 4. 1. , 2. , 3. , 4. 1. , 2. , 3. , 4.
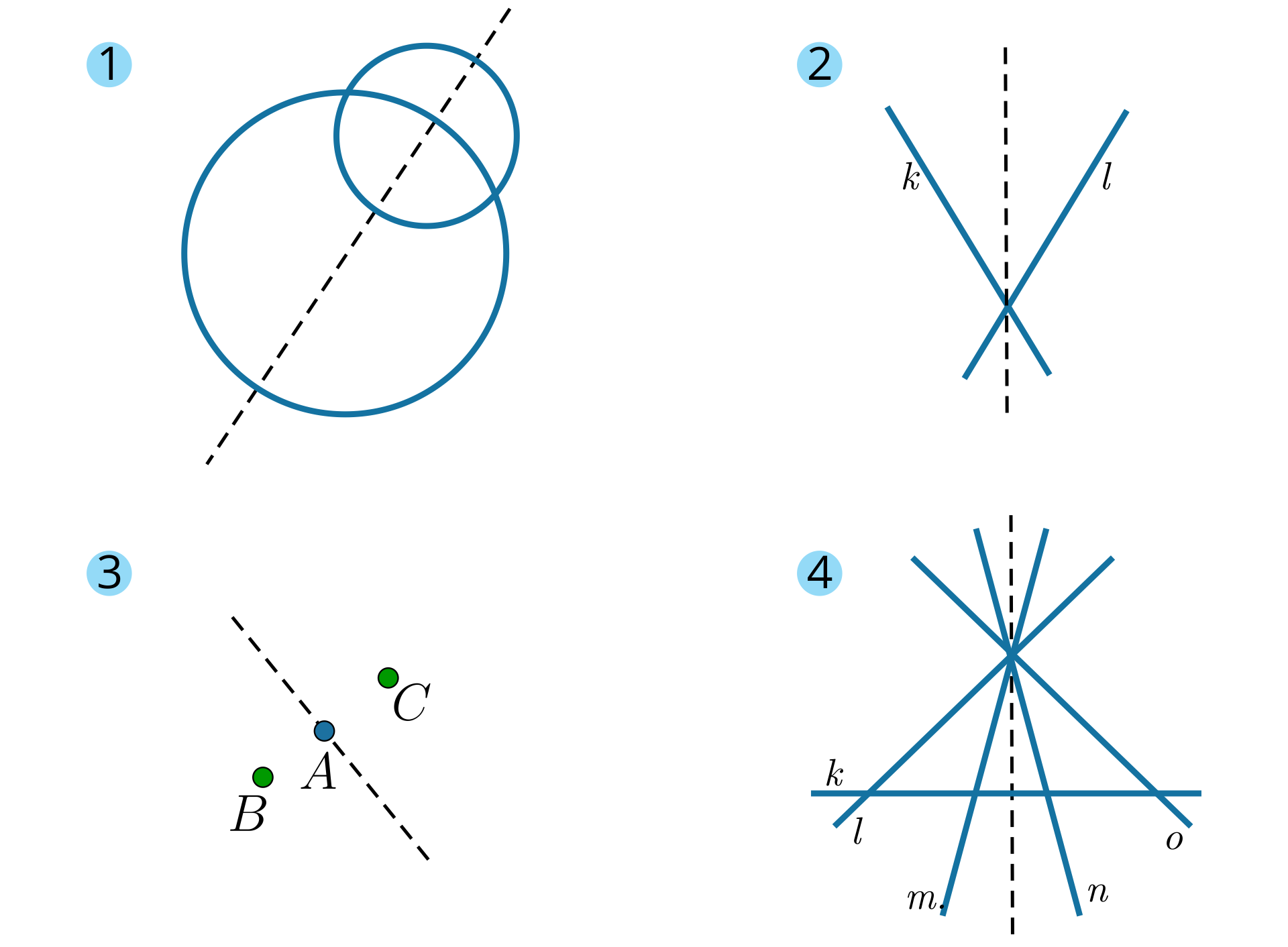
Narysuj figurę , która ma co najmniej jedną oś symetrii i która składa się z
dwóch okręgów,
dwóch prostych,
trzech punktów,
pięciu prostych.
Podaj przykład figury, która ma co najmniej jedną oś symetrii i która składa się z
dwóch okręgów,
dwóch prostych,
trzech punktów,
pięciu prostych.
Kliknij w lukę, aby rozwinąć listę, i wybierz prawidłowe wyrażenie. Jedną z osi symetrii odcinka jest jego 1. cięciwa, 2. dwie, 3. trzy, 4. symetralna, 5. dwusieczna.Osią symetrii kąta ostrego jest jego 1. cięciwa, 2. dwie, 3. trzy, 4. symetralna, 5. dwusieczna.Trójkąt równoboczny ma 1. cięciwa, 2. dwie, 3. trzy, 4. symetralna, 5. dwusieczna osie symetrii.
Notatnik
Możesz skorzystać z poniższego pola tekstowego do zapisania swoich notatek, rozwiązań zadań i innych informacji, które uważasz za potrzebne.