Ciągi – suma wyrazów ciągu arytmetycznego
Materiał ten poświęcony jest sumie wyrazów ciągu arytmetycznego. Analizując zawarte tu przykłady, dowiesz się w jaki sposób stosować twierdzenie o sumie wyrazów ciągu arytmetycznego do rozwiązywania różnego rodzaju zadań.
Symbolem oznaczamy sumę początkowych wyrazów ciągu , czyli

Film dostępny pod adresem /preview/resource/RL2eFzX5Zqw0V
Animacja ilustruje sumę S z indeksem dolnym n początkowych n wyrazów ciągu arytmetycznego a z indeksem dolnym n. Suma S z indeksem dolnym n początkowych n = ułamek w liczniku a z indeksem dolnym jeden plus a z indeksem dolnym n mianownik 2 koniec ułamka razy n.
Suma początkowych wyrazów ciągu arytmetycznego jest równa .
Oblicz sumę .
Sumowane liczby tworzą ciąg arytmetyczny, w którym oraz . Mamy więc
Oblicz sumę stu początkowych liczb naturalnych, które podzielone przez dają resztę .
Pierwszą liczbą naturalną, która podzielona przez daje resztę jest , drugą , trzecią . Liczby te tworzą ciąg arytmetyczny o różnicy . Suma stu początkowych wyrazów tego ciągu jest równa
Rozwiąż równanie z niewiadomą .
Liczby, które sumujemy po lewej stronie równania, są kolejnymi wyrazami ciągu arytmetycznego o pierwszym wyrazie , różnicy . Suma ta składa się z wyrazów.
Ponieważ jest liczbą wyrazów, więc jest liczbą całkowitą dodatnią. Ze wzoru na sumę początkowych wyrazów ciągu arytmetycznego mamy
Z treści zadania wynika, że
Otrzymaliśmy równanie kwadratowe , które ma dwa rozwiązania oraz . Tylko druga z liczb jest całkowita dodatnia. Zatem rozwiązaniem równania jest liczba .
Liczby , , są w podanej kolejności trzema początkowymi wyrazami ciągu arytmetycznego . Oblicz sumę .
Pierwszy wyraz ciągu jest równy , a różnica ciągu jest równa .
sposób :
Zauważmy, że
Ponieważ
oraz
więc
sposób :
Możemy zauważyć, że wyrazy , , , ..., , które mamy zsumować, są kolejnymi wyrazami ciągu arytmetycznego , który składa się z wyrazów i w którym
oraz
Suma początkowych wyrazów tego ciągu jest więc równa
Korzystając z wykresu ciągu arytmetycznego, uzupełnij sumy wyrazów odpowiednimi wartościami.
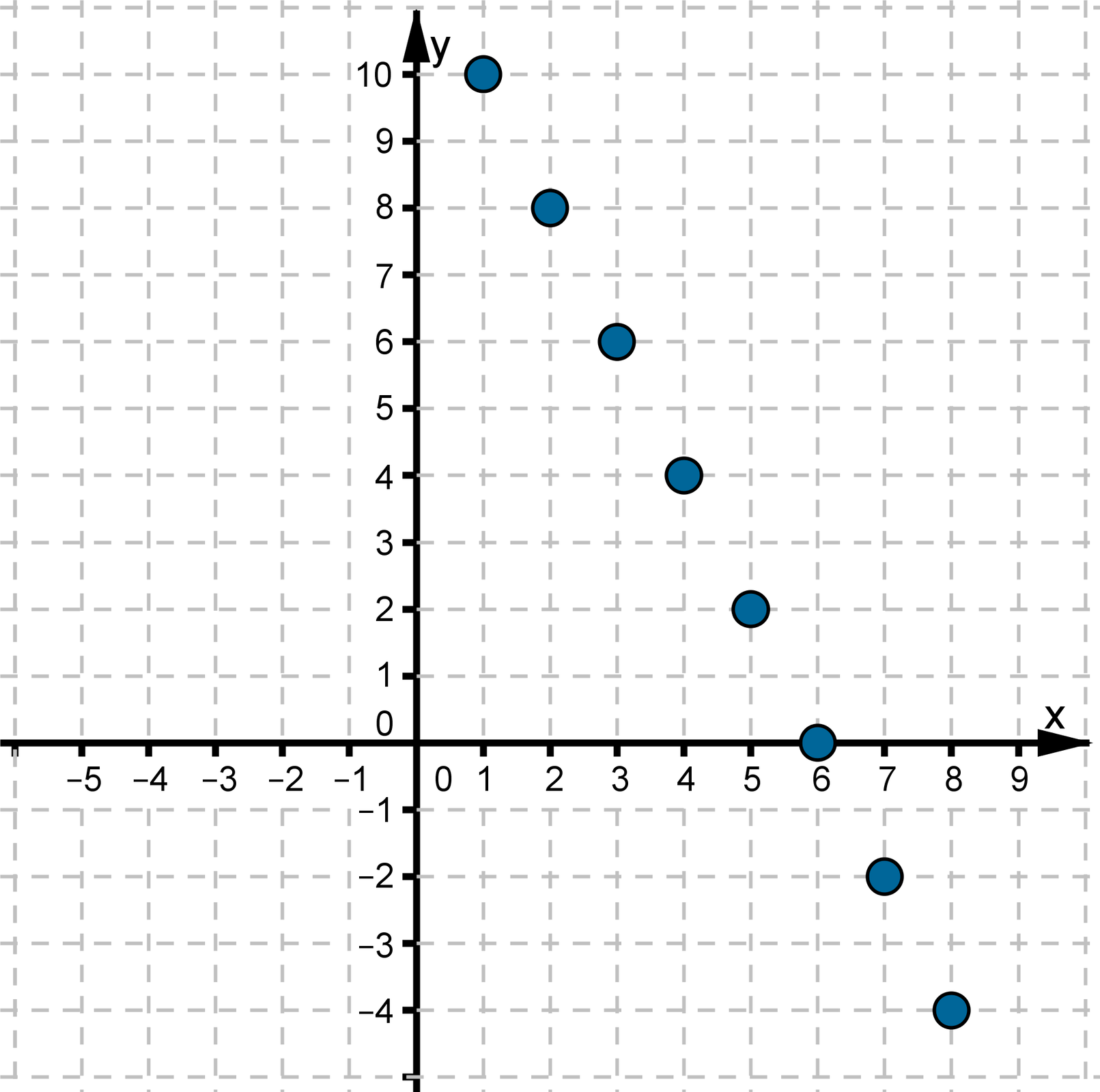
- Piąty wyraz tego ciągu jest równy
- Różnica tego ciągu jest równa
Sumę pewnego ciągu arytmetycznego można zapisać wzorem: .
Połącz w pary.
<span aria-label="a indeks dolny, jeden" role="math"><math><msub><mi>a</mi><mn>1</mn></msub></math></span>, <span aria-label="a indeks dolny, pięć" role="math"><math><msub><mi>a</mi><mn>5</mn></msub></math></span>, <span aria-label="a indeks dolny, dwa" role="math"><math><msub><mi>a</mi><mn>2</mn></msub></math></span>, <span aria-label="a indeks dolny, cztery" role="math"><math><msub><mi>a</mi><mn>4</mn></msub></math></span>, <span aria-label="a indeks dolny, trzy" role="math"><math><msub><mi>a</mi><mn>3</mn></msub></math></span>
Wyznacz pierwszy wyraz i różnicę ciągu arytmetycznego, w którym sumy ośmiu i trzynastu początkowych wyrazów są równe , .
Wykaż, że .
Wykaż, że .