Figury podobne
Materiał ten poświęcony jest figurom podobnym. Analizując zawarte tu przykłady, dowiesz się, jak wyznaczyć skalę podobieństwa figur oraz jak obliczyć wymiary figury podobnej, znając tylko skalę jej podobieństwa.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PE3xI2egV
Figury, które mają ten sam kształt, ale które mogą mieć inną wielkość, nazywamy podobnymi.

Figura jest podobna do figury . Symbolicznie zapisujemy
Skala podobieństwa

Film dostępny pod adresem /preview/resource/R1YUS1TpQO8Te
Animacja przedstawia, czym jest skala.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PE3xI2egV

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PE3xI2egV

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PE3xI2egV

Pierwszą z fotografii zmniejszono. Wymiary drugiej fotografii stanowią odpowiednich wymiarów pierwszej fotografii.
Wymiary trzeciej fotografii stanowią odpowiednich wymiarów pierwszej fotografii.
Zatem druga z fotografii jest obrazem pierwszej w skali , a trzecia jest obrazem pierwszej w skali .
Prostokąty, w kształcie których są fotografie, to figury podobne. Powiemy, że drugi jest podobny do pierwszego w skali , a trzeci do pierwszego w skali .
Skalą podobieństwa nazywamy liczbę , wyrażającą stosunek odpowiadających sobie odcinków w figurach podobnych.
Figurę przedstawiono w skali , otrzymując figurę .

Figury i to figury podobne. Figura jest podobna do figury w skali . Figura jest podobna do figury w skali .
Niech figury i będą podobne w skali .
Jeśli , są punktami figury , a punkty , są odpowiadającymi im punktami figury , to .
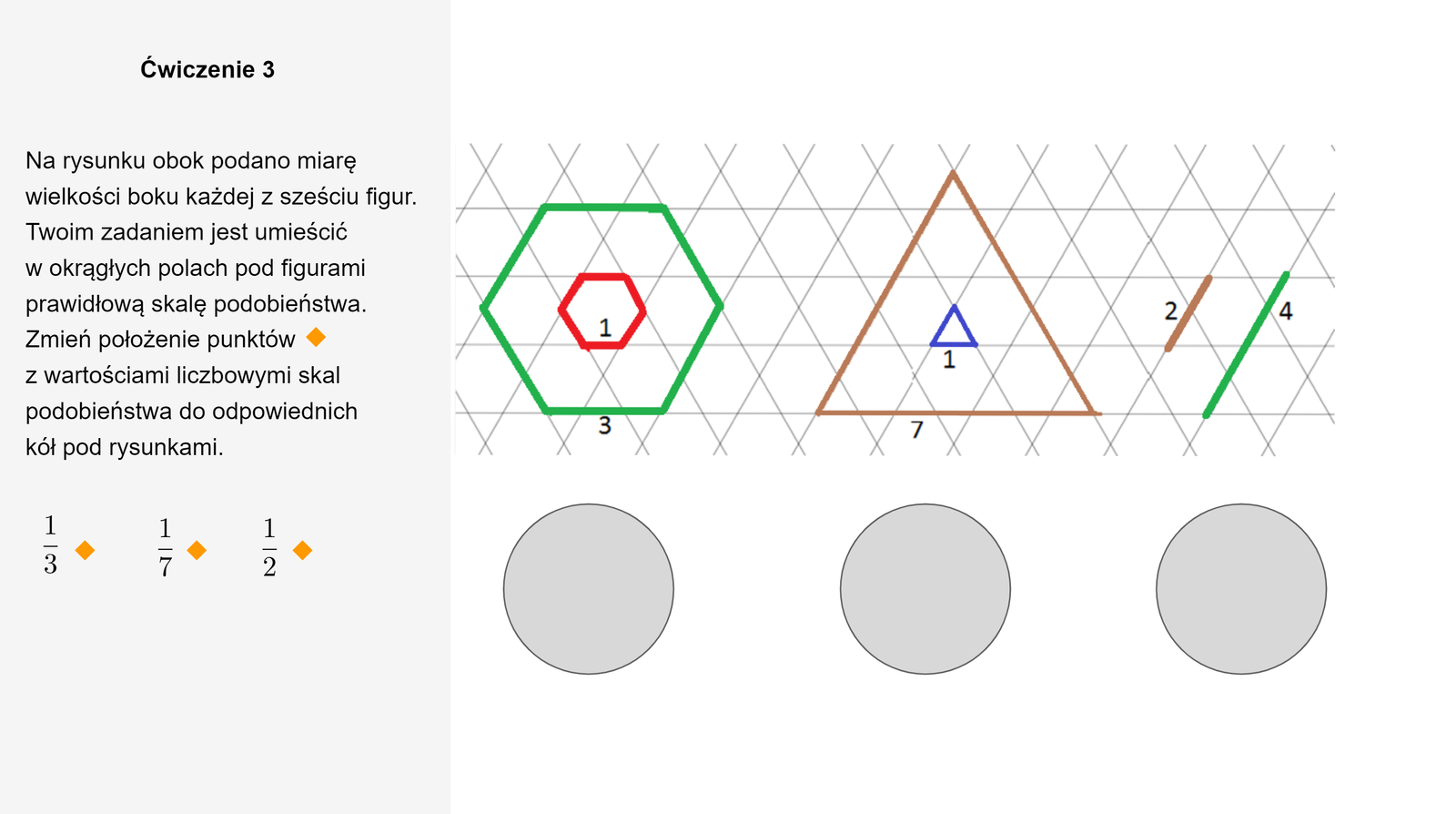
Określ skalę podobieństwa figur.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PE3xI2egV
Okrąg jest podobny do okręgu w skali . Średnica okręgu jest równa . Oblicz pole koła, którego promień jest równy promieniowi okręgu .
Oznaczmy:
– średnica okręgu ,
– średnica okręgu .
Okrąg jest podobny do okręgu w skali . Zapisujemy wynikającą stąd proporcję i wyznaczamy średnicę drugiego z okręgów.
Średnica okręgu jest równa , zatem promień tego okręgu wynosi .
Obliczamy pole koła o promieniu .
Pole koła jest równe .
Każde dwie figury przystające są podobne. Ich skala podobieństwa wynosi .
Ogrodzenie zbudowane jest z elementów, z których każdy podobny jest do sąsiedniego w skali .

W skład porcelanowego serwisu do kawy wchodzi filiżanek, podobnych jedna do drugiej w skali .

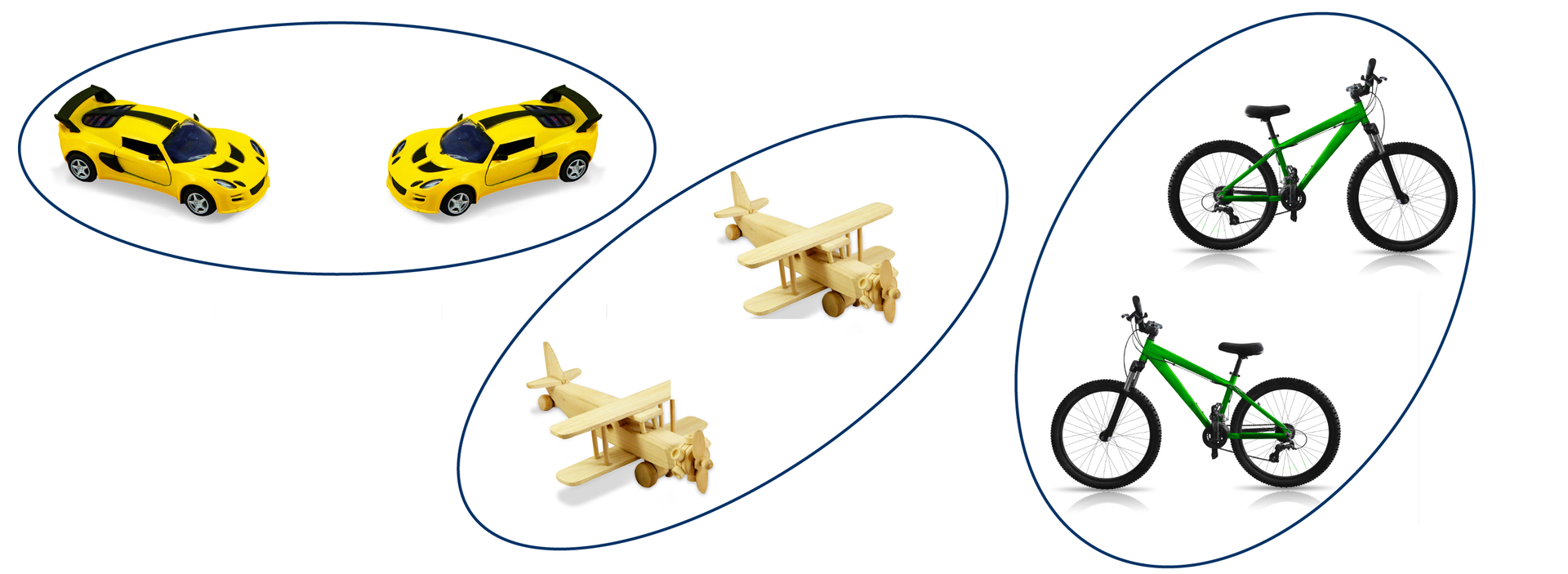
Przykłady figur podobnych.
W życiu codziennym często spotykamy się z obiektami, które przypominają figury podobne.

Film dostępny pod adresem /preview/resource/R17VLg7UUOP1f
Animacja przedstawia, że rosyjska zabawka o nazwie matrioszka składa się z figur podobnych.
Figury geometryczne podobne to na przykład:
dwa dowolne odcinki,
dwa dowolne okręgi,
dwa dowolne kwadraty.
RgE4mB7IdraPe1 Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
Każde dwa odcinki są podobne. Każde dwa okręgi są podobne. Każde dwa kwadraty są podobne.

Każde dwie kule są podobne.
Każde dwa sześciany są podobne.
Na planie wykonanym w skali dywan leżący w pokoju Wieśka jest przedstawiony jako kwadrat o przekątnej długości . W rzeczywistości dywan leży pośrodku pokoju i jest oddalony od każdej ze ścian o . Oblicz pole powierzchni podłogi pokoju Wieśka.
Kwadrat, w kształcie którego jest dywan leżący w pokoju Wieśka, jest podobny w skali do kwadratu przedstawiającego go na planie.
Obliczmy rzeczywistą długość przekątnej dywanu.
Korzystamy ze wzoru na długość przekątnej kwadratu i obliczamy długość boku kwadratu.
Teraz możemy obliczyć długość boku kwadratu, w kształcie którego jest podłoga.
Obliczamy pole powierzchni podłogi – jako pole kwadratu.
Pole powierzchni podłogi pokoju Wieśka jest równe około .
Otrzymywanie figur podobnych
Pokażemy na przykładach, jak można skonstruować figurę podobną do danej.
Skonstruujemy odcinek podobny do danego odcinka w skali .

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PE3xI2egV
Wyobraź sobie dowolny czworokąt. Zaproponuj sposób konstrukcji figury podobnej w skali do tego czworokąta.
Narysuj dowolny czworokąt.
Zaproponuj sposób konstrukcji figury podobnej w skali do tego czworokąta.
- Każde dwa okręgi o równych obwodach są podobne.
- Każde dwa prostopadłe odcinki są podobne.
- Każde dwa kąty są podobne.
- Okrąg o promieniu r jest podobny do koła o promieniu .
- Prosta jest podobna do odcinka, który jest do niej równoległy.
- ,
- ,
- ,
- ,
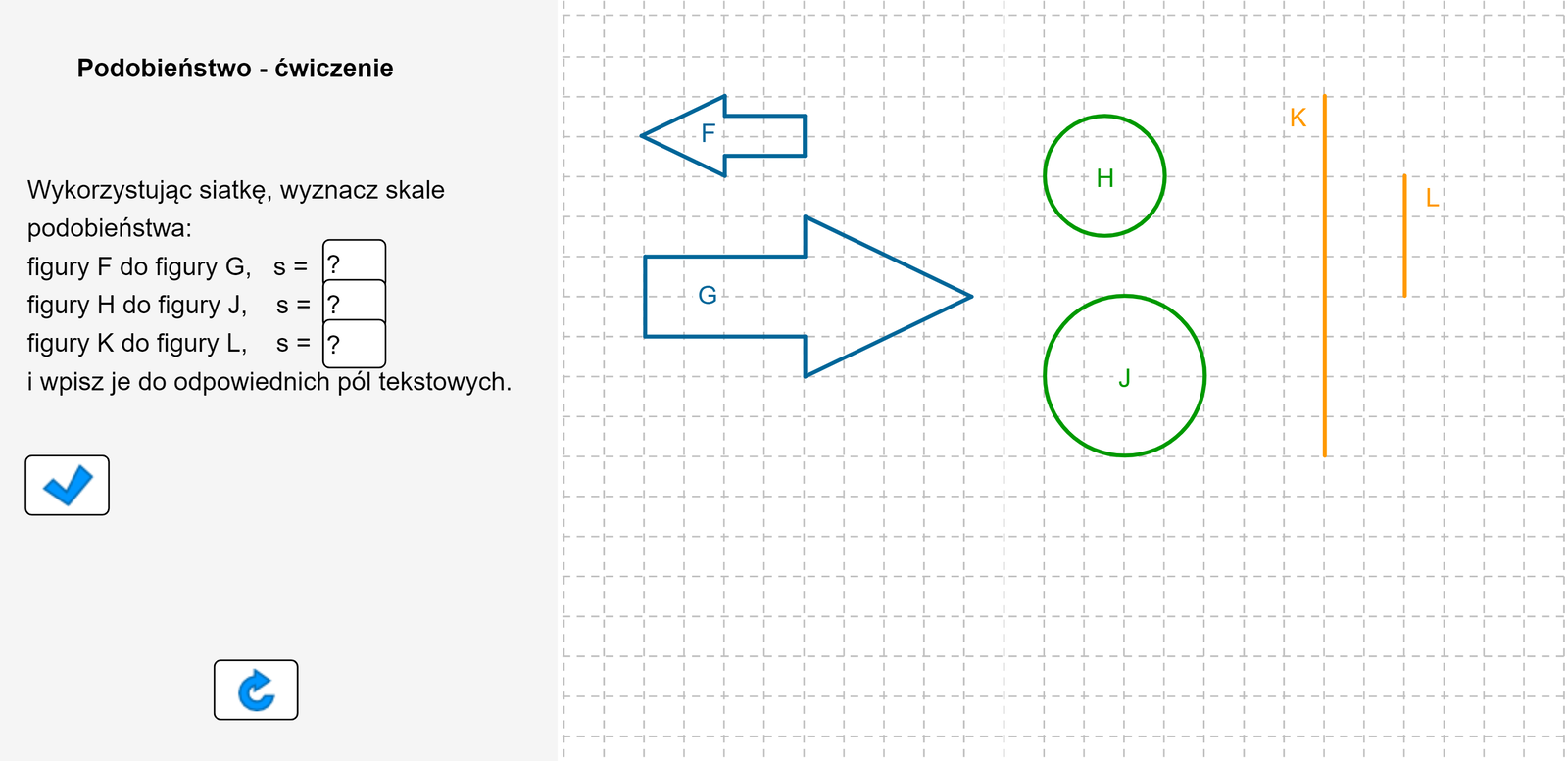
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PE3xI2egV
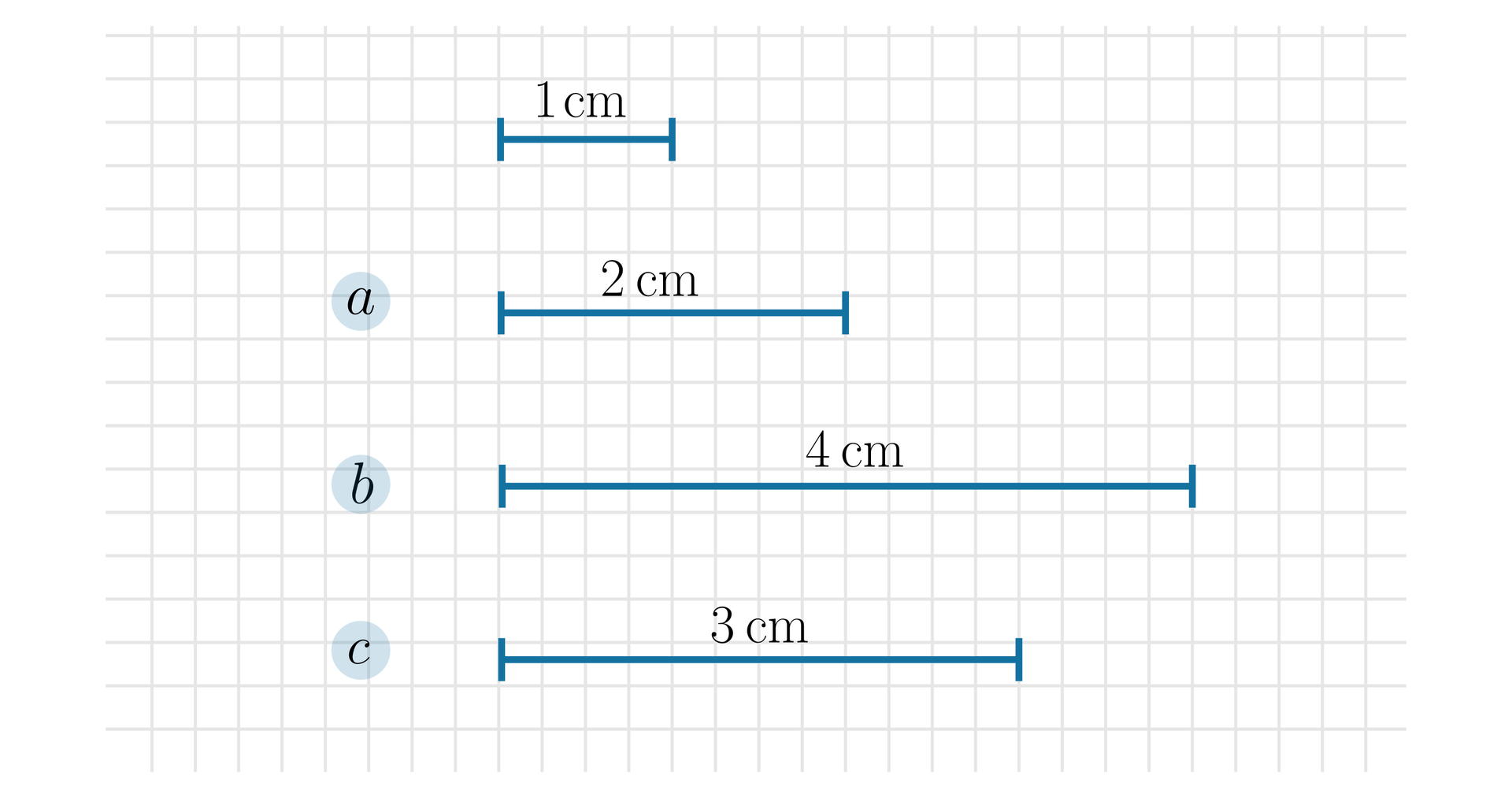
Narysuj dowolny odcinek.
Znajdź konstrukcyjnie odcinek
dwa razy dłuższy,
cztery razy dłuższy,
trzy razy dłuższy.
Narysuj trzy różne odcinki i oznacz ich długości literami , i . Podaj długość odcinka , aby spełniona była każda z poniższych równości.
Wyobraź sobie trzy odcinki różnej długości. Oznaczmy je literami , i . Zastanów się, jaką długość musi mieć odcinek , aby spełniona była każda z poniższych równości.
Udowodnij, że każda figura osiowosymetryczna składa się z dwóch figur podobnych.
Udowodnij, że dwusieczna kąta dzieli ten kąt na dwa kąty podobne.
Figura jest podobna do figury w skali . Figura jest podobna do figury w skali . Czy figury i są podobne? Jeśli tak, to w jakiej skali? Jeśli nie, podaj przykład.
Figura jest podobna do figury w skali . Figura jest przystająca do figury
. Czy figury i są podobne? Jeśli tak, to w jakiej skali? Jeśli nie, podaj przykład.
- Figura będąca obrazem figury w symetrii osiowej jest podobna do figury .
- Każde dwie figury podobne są przystające.
- Każde dwa wycinki danego koła są podobne.
- Figura będąca obrazem figury w symetrii środkowej jest podobna do figury .
- Promień koła jest równy .
- Obwód koła K2 jest równy .
- Pole koła jest o większe od pola koła .
Pole odcinka kołowego wynosi 1. , 2. , 3. , 4. .
Uzupełnij tabelę, przeciągając do niej prawidłowe wartości.