Galeria zdjęć interaktywnych
Polecenie 1
Zapoznaj się z galerią zdjęć interaktywnych i różnymi sposobami przedstawiania danych graficznych. Zinterpretuj prezentowane wykresy.
Ilustracja interaktywna zatytułowana „Hisotgram Diagram”. Na podstawie podanego szeregu statystycznego sporządzimy histogram i diagram obrazujące rozkład czasu obsługi klienta na pewnej stacji benzynowej. Po lewo umieszczono tabelę z dwiema kolumnami i sześcioma wierszami. Lewa kolumn tabeli określona jest w wierszu nagłówkowym jako „czas obsługi klienta na stacji benyzowej w minutach”, na poniższych wykresach opisany na poziomej osi jako . Niżej mamy podane przedziały czasowe. Prawa kolumna dotyczy liczby klientów, która na poniższych wykresach opisana jest na pionowej osi . Dane podane w tabeli są następujące: Czas od zera do czterech minut poświęcono na obsługę czterech klientów. Czas od czterech do ośmiu minut poświęcono sześciu klientom. Czas od ośmiu do dwunastu minut poświęcono ośmiu klientom, a czas od dwunastu do szesnastu minut poświęcono dwóm klientom. Poniżej umieszczono obok siebie dwa wykresy prezentujące dane z tabeli. Oba wykresy są przedstawione za pomocą dwóch półosi: poziomej (jest to czas obsługi w minutach) od zera do szesnastu z podziałką co cztery. Półoś pionowa opisana jest jako i przedstawia liczbę klientów od zera do ośmiu. Po lewej stronie umieszczono Histogram czasu obsługi klienta, po prawej Diagram czasu obsługi klienta. Lewy wykres jest wykresem słupkowym. Opis histogramu: Jednym z graficznych sposobów przedstawiania rozkładu empirycznego cechy jest histogram. Histogram zbudowany jest z prostokątów, których podstawy umieszczone na osi układu współrzędnych wyznaczone są przez przedziały klasowe wartości cechy. Wysokości określa liczebność elementów zawartych w danych przedziałach klasowych. W diagramie z kolei narysowano słupki, przy czym każdy słupek podzielony jest na pół linią przerywaną biegnącą wzdłuż każdego słupka. Na szczycie każdego słupka w miejscu, gdzie zaczyna się linia przerywana umieszczono kolorowe punkty, które połączono łamaną. Punkty te mają współrzędne: . Opis diagramu: Diagramem będziemy nazywać łamaną, otrzymaną z histogramu, po połączeniu odcinkami środków przedziałów klasowych wyznaczonych na górnych bokach prostokątów.
Ilustracja interaktywna zatytułowana „Hisotgram Diagram”. Na podstawie podanego szeregu statystycznego sporządzimy histogram i diagram obrazujące rozkład czasu obsługi klienta na pewnej stacji benzynowej. Po lewo umieszczono tabelę z dwiema kolumnami i sześcioma wierszami. Lewa kolumn tabeli określona jest w wierszu nagłówkowym jako „czas obsługi klienta na stacji benyzowej w minutach”, na poniższych wykresach opisany na poziomej osi jako . Niżej mamy podane przedziały czasowe. Prawa kolumna dotyczy liczby klientów, która na poniższych wykresach opisana jest na pionowej osi . Dane podane w tabeli są następujące: Czas od zera do czterech minut poświęcono na obsługę czterech klientów. Czas od czterech do ośmiu minut poświęcono sześciu klientom. Czas od ośmiu do dwunastu minut poświęcono ośmiu klientom, a czas od dwunastu do szesnastu minut poświęcono dwóm klientom. Poniżej umieszczono obok siebie dwa wykresy prezentujące dane z tabeli. Oba wykresy są przedstawione za pomocą dwóch półosi: poziomej (jest to czas obsługi w minutach) od zera do szesnastu z podziałką co cztery. Półoś pionowa opisana jest jako i przedstawia liczbę klientów od zera do ośmiu. Po lewej stronie umieszczono Histogram czasu obsługi klienta, po prawej Diagram czasu obsługi klienta. Lewy wykres jest wykresem słupkowym. Opis histogramu: Jednym z graficznych sposobów przedstawiania rozkładu empirycznego cechy jest histogram. Histogram zbudowany jest z prostokątów, których podstawy umieszczone na osi układu współrzędnych wyznaczone są przez przedziały klasowe wartości cechy. Wysokości określa liczebność elementów zawartych w danych przedziałach klasowych. W diagramie z kolei narysowano słupki, przy czym każdy słupek podzielony jest na pół linią przerywaną biegnącą wzdłuż każdego słupka. Na szczycie każdego słupka w miejscu, gdzie zaczyna się linia przerywana umieszczono kolorowe punkty, które połączono łamaną. Punkty te mają współrzędne: . Opis diagramu: Diagramem będziemy nazywać łamaną, otrzymaną z histogramu, po połączeniu odcinkami środków przedziałów klasowych wyznaczonych na górnych bokach prostokątów.Ilustracja interaktywna dotycząca Wykresu złożonego, czyli kombinowanego. Opis: Wykres złożony obrazuje zależność między przeciętną płacą w pewnym zakładzie pracy a przeciętną masą spożywanej rocznie czekolady przez jednego pracownika. Opis audio: Wykres złożony łączy różne formy graficzne (np. wykres słupkowy i wykres liniowy). Za jego pomocą można zaobserwować zależności między zjawiskami (np. między zmianą wysokości płac a strukturą zakupów). Koniec opisu. Poniżej umieszczono wykres z dwiema półosiami, natomiast dane opisane są w trojaki sposób: za pomocą dwóch osi i linii pomocniczych. Na poziomej półosi przedstawiono lata od 2013 do 2019. Na pionowej półosi przedstawiono kwoty z złotówkach od zera do sześciu tysięcy z podziałką co tysiąc. Na poziomie każdego tysiąca poprowadzono poziomą linię pomocniczą wzdłuż osi czasu. Linie pomocnicze opisano z prawej strony wykresu. Od dołu mamy następująco: na poziomie osi czasu 0 gram, na poziomie tysiąca złotych 150 gram, na poziomie dwóch tysięcy złotych 300 gram, na poziomie trzech tysięcy złotych 450 gram, na poziomie czterech tysięcy złotych 600 gram, na poziomie pięciu tysięcy złotych 750 gram i na poziomie sześciu tysięcy złotych 900 gram. Dane reprezentowane są jednocześnie za pomocą siedmiu pionowych słupków (jeden słupek przypada na jeden rok), przy czym słupki prezentują przeciętną płacę w złotówkach oraz za pomocą łamanej umieszczonej nad słupkami reprezentującą masę spożywanej rocznie czekolady w gramach. Słupki osiągają w kolejnych latach następujące wysokości: 2013 rok to 3000 złotych, 2014 rok to około 3900 złotych, 2015 rok to 4000 złotych, 2016 rok to około 2100 złotych, 2017 rok to 5000 złotych, 2018 rok to około 4800 złotych, 2019 rok to około 3500 złotych. Łamana ma wierzchołki, w których podamy kolejno: rok, płacę, masę czekolady. Wierzchołki te to: (2013 rok, 4000 złotych, 600 gram), (2014 rok, 4500 złotych, 675 gram), (2015 rok, około 5900 złotych, około 880 gram), (2016 rok, około 5200 złotych, około 770 gram), (2017 rok, około 5200 złotych, około 770 gram), (2018 rok, około 4900 złotych, około 730 gram), (2019 rok, około 4000 złotych, około 600 gram).
Ilustracja interaktywna dotycząca Wykresu złożonego, czyli kombinowanego. Opis: Wykres złożony obrazuje zależność między przeciętną płacą w pewnym zakładzie pracy a przeciętną masą spożywanej rocznie czekolady przez jednego pracownika. Opis audio: Wykres złożony łączy różne formy graficzne (np. wykres słupkowy i wykres liniowy). Za jego pomocą można zaobserwować zależności między zjawiskami (np. między zmianą wysokości płac a strukturą zakupów). Koniec opisu. Poniżej umieszczono wykres z dwiema półosiami, natomiast dane opisane są w trojaki sposób: za pomocą dwóch osi i linii pomocniczych. Na poziomej półosi przedstawiono lata od 2013 do 2019. Na pionowej półosi przedstawiono kwoty z złotówkach od zera do sześciu tysięcy z podziałką co tysiąc. Na poziomie każdego tysiąca poprowadzono poziomą linię pomocniczą wzdłuż osi czasu. Linie pomocnicze opisano z prawej strony wykresu. Od dołu mamy następująco: na poziomie osi czasu 0 gram, na poziomie tysiąca złotych 150 gram, na poziomie dwóch tysięcy złotych 300 gram, na poziomie trzech tysięcy złotych 450 gram, na poziomie czterech tysięcy złotych 600 gram, na poziomie pięciu tysięcy złotych 750 gram i na poziomie sześciu tysięcy złotych 900 gram. Dane reprezentowane są jednocześnie za pomocą siedmiu pionowych słupków (jeden słupek przypada na jeden rok), przy czym słupki prezentują przeciętną płacę w złotówkach oraz za pomocą łamanej umieszczonej nad słupkami reprezentującą masę spożywanej rocznie czekolady w gramach. Słupki osiągają w kolejnych latach następujące wysokości: 2013 rok to 3000 złotych, 2014 rok to około 3900 złotych, 2015 rok to 4000 złotych, 2016 rok to około 2100 złotych, 2017 rok to 5000 złotych, 2018 rok to około 4800 złotych, 2019 rok to około 3500 złotych. Łamana ma wierzchołki, w których podamy kolejno: rok, płacę, masę czekolady. Wierzchołki te to: (2013 rok, 4000 złotych, 600 gram), (2014 rok, 4500 złotych, 675 gram), (2015 rok, około 5900 złotych, około 880 gram), (2016 rok, około 5200 złotych, około 770 gram), (2017 rok, około 5200 złotych, około 770 gram), (2018 rok, około 4900 złotych, około 730 gram), (2019 rok, około 4000 złotych, około 600 gram).Ilustracja interaktywna opisująca wykres warstwowy. Opis: Wykres przedstawia liczbę książek wypożyczonych w pewnej bibliotece szkolnej w ciągu kilku dni lutego. Opis audio: Mając do czynienia z kilkoma zbiorowościami powiązanymi ze sobą logicznie, możemy zaobserwować zmiany w czasie w poziomie liczebności poszczególnych zbiorowości i zmiany zachodzące w ich strukturze, za pomocą wykresów warstwowych. Koniec opisu. Pod opisami umieszczono przestrzenny wykres, w którym pozioma półoś opisuje czas: czwarty, piąty, szósty, siódmy i dziesiąty lutego 2020, a pionowa półoś opisuje liczbę książek od zera do czterdziestu z podziałką co pięć. W przestrzennym wykresie umieszczono ścianę o pewnej grubości, której ma nieregularny zygzakowaty kształt przypominający łamaną. Ściana ta składa się z dwóch części oddzielonych od siebie również nieregularnym zygzakiem, który ma tutaj inny kształt, niż zygzak w szczycie ściany. Dolna część ściany jest niebieska i dotyczy liczby książek z działu literatura polska, górna część ściany dotyczy literatury zagranicznej. Najpierw opiszemy liczbę wypożyczonych książek z działu literatury polskiej. Mamy tu swego rodzaju wierzchołki jak w przypadku łamanej w dwóch wymiarach. Wierzchołki określimy parametrami dzień i liczba. Wierzchołki dla literatury polskiej są następujące: (czwarty lutego, 24 książki), (piąty lutego, 30 książek), (szósty lutego, 25 książek), (siódmy lutego, 10 książek), (dziesiąty lutego, 15 książek). Jako że kawałek ściany opisujący literaturę zagraniczną jest osadzony na kawałku dotyczącym literatury polskiej, to od wysokości szczytowych należy odjąć dolny wierzchołek tej ściany, to znaczy dla czwartego lutego mamy w literaturze zagranicznej 36 wypożyczeń łącznie, ale 24 książki były z zakresu literatury polskiej. Mamy więc po odjęciu 12 książek z literatury zagranicznej. I tak postępujemy w każdym wierzchołku. Wierzchołki dla literatury zagranicznej są następujące: (czwarty lutego, 36 książek łącznie, zagraniczna 12 książek), (piąty lutego, 39 książek łącznie, zagraniczna 9 książek), (szósty lutego, 30 książek łącznie, zagraniczna 5 książek), (siódmy lutego, 30 książek łącznie, zagraniczna 20 książek), (dziesiąty lutego, 21 książek łącznie, zagraniczna 6 książek).
Ilustracja interaktywna opisująca wykres warstwowy. Opis: Wykres przedstawia liczbę książek wypożyczonych w pewnej bibliotece szkolnej w ciągu kilku dni lutego. Opis audio: Mając do czynienia z kilkoma zbiorowościami powiązanymi ze sobą logicznie, możemy zaobserwować zmiany w czasie w poziomie liczebności poszczególnych zbiorowości i zmiany zachodzące w ich strukturze, za pomocą wykresów warstwowych. Koniec opisu. Pod opisami umieszczono przestrzenny wykres, w którym pozioma półoś opisuje czas: czwarty, piąty, szósty, siódmy i dziesiąty lutego 2020, a pionowa półoś opisuje liczbę książek od zera do czterdziestu z podziałką co pięć. W przestrzennym wykresie umieszczono ścianę o pewnej grubości, której ma nieregularny zygzakowaty kształt przypominający łamaną. Ściana ta składa się z dwóch części oddzielonych od siebie również nieregularnym zygzakiem, który ma tutaj inny kształt, niż zygzak w szczycie ściany. Dolna część ściany jest niebieska i dotyczy liczby książek z działu literatura polska, górna część ściany dotyczy literatury zagranicznej. Najpierw opiszemy liczbę wypożyczonych książek z działu literatury polskiej. Mamy tu swego rodzaju wierzchołki jak w przypadku łamanej w dwóch wymiarach. Wierzchołki określimy parametrami dzień i liczba. Wierzchołki dla literatury polskiej są następujące: (czwarty lutego, 24 książki), (piąty lutego, 30 książek), (szósty lutego, 25 książek), (siódmy lutego, 10 książek), (dziesiąty lutego, 15 książek). Jako że kawałek ściany opisujący literaturę zagraniczną jest osadzony na kawałku dotyczącym literatury polskiej, to od wysokości szczytowych należy odjąć dolny wierzchołek tej ściany, to znaczy dla czwartego lutego mamy w literaturze zagranicznej 36 wypożyczeń łącznie, ale 24 książki były z zakresu literatury polskiej. Mamy więc po odjęciu 12 książek z literatury zagranicznej. I tak postępujemy w każdym wierzchołku. Wierzchołki dla literatury zagranicznej są następujące: (czwarty lutego, 36 książek łącznie, zagraniczna 12 książek), (piąty lutego, 39 książek łącznie, zagraniczna 9 książek), (szósty lutego, 30 książek łącznie, zagraniczna 5 książek), (siódmy lutego, 30 książek łącznie, zagraniczna 20 książek), (dziesiąty lutego, 21 książek łącznie, zagraniczna 6 książek).Ilustracja interaktywna przedstawia wykres radarowy. Opis: Wykres radarowy przedstawia czas w minutach dojazdu do pracy pana Adama i pana Bogdana w pierwszym tygodniu stycznia 2020 roku. Opis audio: Wykres radarowy (zwany też biegunowym, centrycznym, pajączkowym) wykorzystywany jest w celu porównania zebranych danych dla kilku zbiorowości charakteryzowanych przez tę samą cechę mierzalną lub w celu opisania tej samej zbiorowości przez kilka cech. Dane liczbowe zamieszczone są na półprostych o początkach w środku punktu centralnego, którym jest zwykle środek koła. Ze względu na wygląd, przypominający koło, w mierze kątowej odznacza się zazwyczaj cykl czasowy, a wzdłuż promieni wartość liczbową. Koniec opisu. Poniżej umieszczono wykres przypominający pajęczą sieć. Jest on pięciokątem foremnym, w którym umieszczono równo coraz mniejsze pięciokąty foremne tak, że wszystkie figury mają wspólny środek. Łącznie mamy na rysunku siedem figur. Ze środka do wierzchołków wyprowadzono odcinki przez wszystkie figury aż do największego pięciokąta. Jego wierzchołki oznaczają kolejne dni. Zaczynając od górnego wierzchołka, mamy następujące daty: siódmy stycznia 2020, ósmy stycznia 2020, dziewiąty stycznia 2020, dziesiąty stycznia 2020 i jedenasty stycznia 2020. Każdy pięciokąt oznacza inny czas w minutach. We wspólnym środku oznaczono zero, następnie najmniejszy pięciokąt reprezentuje pięć minut, kolejny dziesięć i tak co pięć do trzydziestu pięciu. Dane na wykresie radarowym są przedstawione w formie dwóch nieforemnych pięciokątów o wierzchołkach położonych na odcinkach łączących środek z wierzchołkami figur. Jeden pięciokąt nieforemny dotyczy pana Adama, drugi pana Bogdana. Pięciokąt opisujący drogę do pracy pana Adama ma następujące wierzchołki: (siódmy stycznia, 32 minuty), (ósmy stycznia, 33 minuty), (dziewiąty stycznia, 28 minut), (dziesiąty stycznia, 12 minut), (jedenasty stycznia, 16 minut). Pięciokąt opisujący drogę do pracy pana Bogdana ma następujące wierzchołki: (siódmy stycznia, 17 minut), (ósmy stycznia, 20 minut), (dziewiąty stycznia, 12 minut), (dziesiąty stycznia, 16 minut), (jedenasty stycznia, 29 minut).
Ilustracja interaktywna przedstawia wykres radarowy. Opis: Wykres radarowy przedstawia czas w minutach dojazdu do pracy pana Adama i pana Bogdana w pierwszym tygodniu stycznia 2020 roku. Opis audio: Wykres radarowy (zwany też biegunowym, centrycznym, pajączkowym) wykorzystywany jest w celu porównania zebranych danych dla kilku zbiorowości charakteryzowanych przez tę samą cechę mierzalną lub w celu opisania tej samej zbiorowości przez kilka cech. Dane liczbowe zamieszczone są na półprostych o początkach w środku punktu centralnego, którym jest zwykle środek koła. Ze względu na wygląd, przypominający koło, w mierze kątowej odznacza się zazwyczaj cykl czasowy, a wzdłuż promieni wartość liczbową. Koniec opisu. Poniżej umieszczono wykres przypominający pajęczą sieć. Jest on pięciokątem foremnym, w którym umieszczono równo coraz mniejsze pięciokąty foremne tak, że wszystkie figury mają wspólny środek. Łącznie mamy na rysunku siedem figur. Ze środka do wierzchołków wyprowadzono odcinki przez wszystkie figury aż do największego pięciokąta. Jego wierzchołki oznaczają kolejne dni. Zaczynając od górnego wierzchołka, mamy następujące daty: siódmy stycznia 2020, ósmy stycznia 2020, dziewiąty stycznia 2020, dziesiąty stycznia 2020 i jedenasty stycznia 2020. Każdy pięciokąt oznacza inny czas w minutach. We wspólnym środku oznaczono zero, następnie najmniejszy pięciokąt reprezentuje pięć minut, kolejny dziesięć i tak co pięć do trzydziestu pięciu. Dane na wykresie radarowym są przedstawione w formie dwóch nieforemnych pięciokątów o wierzchołkach położonych na odcinkach łączących środek z wierzchołkami figur. Jeden pięciokąt nieforemny dotyczy pana Adama, drugi pana Bogdana. Pięciokąt opisujący drogę do pracy pana Adama ma następujące wierzchołki: (siódmy stycznia, 32 minuty), (ósmy stycznia, 33 minuty), (dziewiąty stycznia, 28 minut), (dziesiąty stycznia, 12 minut), (jedenasty stycznia, 16 minut). Pięciokąt opisujący drogę do pracy pana Bogdana ma następujące wierzchołki: (siódmy stycznia, 17 minut), (ósmy stycznia, 20 minut), (dziewiąty stycznia, 12 minut), (dziesiąty stycznia, 16 minut), (jedenasty stycznia, 29 minut).Ilustracja interaktywna przedstawia wykres segmentowy. Opis: Wykres obrazuje strukturę użytkowania ziemi w gospodarstwie pana Włodzimierza. Opis audio: Wykres segmentowy składa się z małych figur (najczęściej kwadratów) ukazujących wielkość danego zjawiska. Szczególnie czytelne są wykresy składające się ze kwadratów odpowiednio pokolorowanych, zgodnie z udziałem procentowym danych zjawisk ( kwadratowi odpowiada na nich udziału zjawiska). Koniec opisu. Wykres jest kwadratem podzielonym na mniejsze kwadraty. Wymiar dużego kwadratu to 10 na 10 małych kwadratów. Małe kwadraty pozaznaczano czterema równymi kolorami, dzieląc je w ten sposób na cztery grupy reprezentujące kolejno: sad (20 kwadratów), łąki i pastwiska (15 kwadratów), teren zabudowany, nieużytki (5 kwadratów), grunty orne (60 kwadratów).
Ilustracja interaktywna przedstawia wykres segmentowy. Opis: Wykres obrazuje strukturę użytkowania ziemi w gospodarstwie pana Włodzimierza. Opis audio: Wykres segmentowy składa się z małych figur (najczęściej kwadratów) ukazujących wielkość danego zjawiska. Szczególnie czytelne są wykresy składające się ze kwadratów odpowiednio pokolorowanych, zgodnie z udziałem procentowym danych zjawisk ( kwadratowi odpowiada na nich udziału zjawiska). Koniec opisu. Wykres jest kwadratem podzielonym na mniejsze kwadraty. Wymiar dużego kwadratu to 10 na 10 małych kwadratów. Małe kwadraty pozaznaczano czterema równymi kolorami, dzieląc je w ten sposób na cztery grupy reprezentujące kolejno: sad (20 kwadratów), łąki i pastwiska (15 kwadratów), teren zabudowany, nieużytki (5 kwadratów), grunty orne (60 kwadratów).Polecenie 2
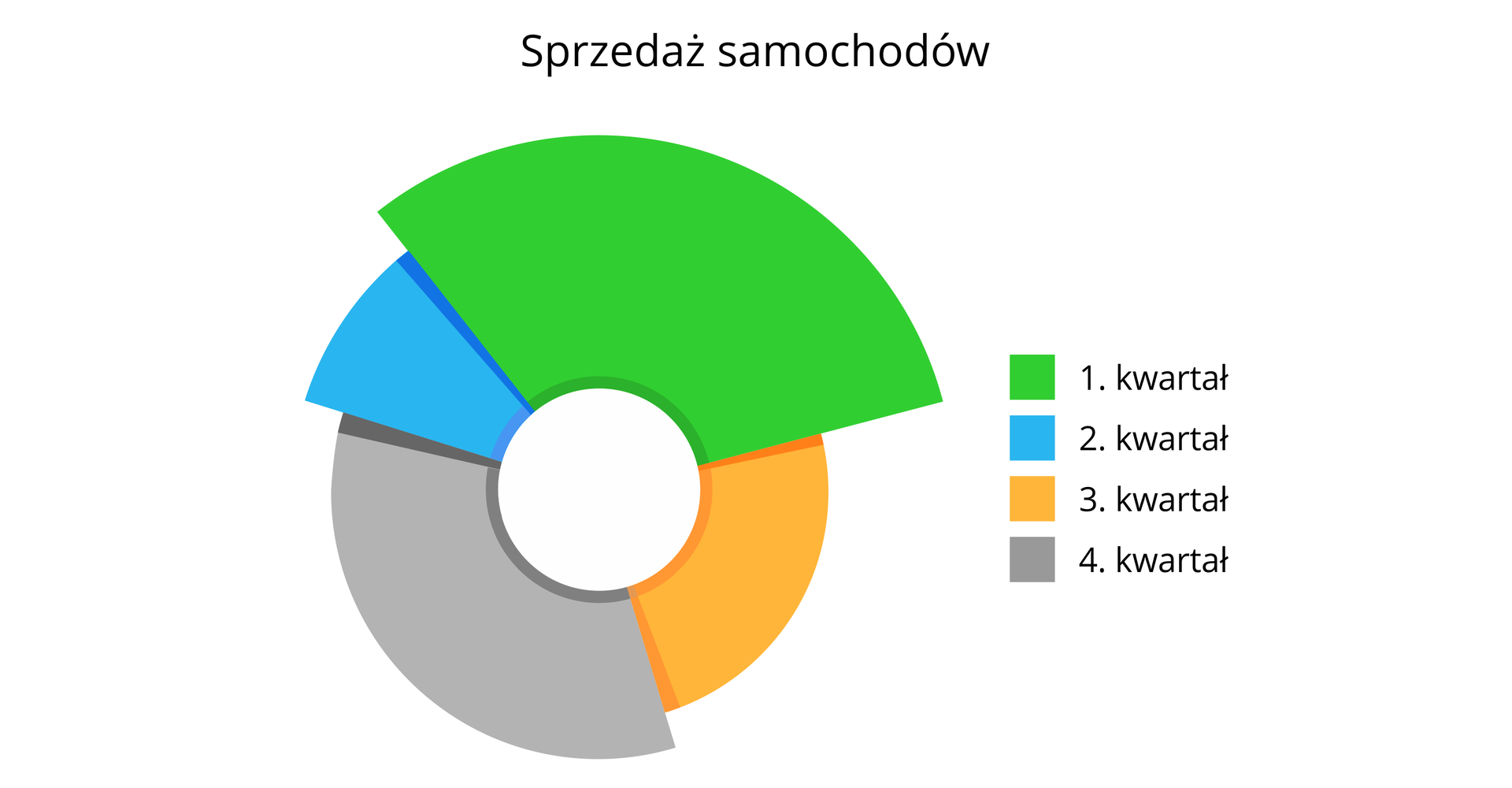
W pewnym salonie samochodowym w 1 kwartale 2019 r. sprzedano samochodów, w kwartale zaledwie samochodów, w kwartale samochodów i w kwartale samochodów.
Sporządź wykres pierścieniowy obrazujący te dane.
Wykres zatytułowany jest „Sprzedaż samochodów” i jest podobny do wykresu kołowego, jednak każdy wycinek oznaczający daną grupę biorącą udział w badaniu, ma coraz mniejszy promień, przy czym wszystkie mają oczywiście wspólny środek. Ze środka wycięte jest koło o małym promieniu, co daje właśnie pierścień. Po prawej umieszczona jest legenda, czyli kwadraty w różnych kolorach oznaczające kwartały. Zauważmy, że łącznie sprzedano 100 samochodów, a 360 stopni podzielone na 100 daje 3 i 6 dziesiątych. Wystarczy więc pomnożyć ilość sprzedanych samochodów w danym kwartale, aby wiedzieć, o jakim kącie wycinek reprezentuje dany kwartał. Mamy więc takie kąty: pierwszy kwartał reprezentuje wycinek pierścienia o kącie 144 stopnie, drugi kwartał 18 stopni, trzeci kwartał 72 stopnie, czwarty kwartał 126 stopni.