Geometria przestrzenna
W tym materiale zawarte są wiadomości dotyczące budowy, pól i objętości figur przestrzennych. Po wykonaniu wszystkich zadań możesz rozwiązać test, który znajduje się na końcu materiału i zawiera zadania utrwalające i rozwijające uzyskane umiejętności.
Aby wyobrazić sobie figurę przestrzenną lub rozpoznać ją, często wystarczają jej widoki z trzech stron: z góry, z przodu i z boku.
Uzupełnij poniższe luki. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną odpowiedź. Bryła zbudowana z sześcianów ma objętość 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .Bryła zbudowana z sześcianów ma objętość 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .Bryła zbudowana z sześcianów ma objętość 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9.
Połącz w pary objętość z odpowiednią bryłą.
- Suma liczby ścian, krawędzi i wierzchołków w ostrosłupie trójkątnym jest równa .
- W ostrosłupie czworokątnym jest razy więcej krawędzi niż ścian.
- Suma liczby krawędzi i wierzchołków w ostrosłupie pięciokątnym jest równa .
- W ostrosłupie jedenastokątnym są o krawędzie więcej niż w ostrosłupie dziewięciokątnym.
Sześcian o krawędzi długości ma pole powierzchni równe .
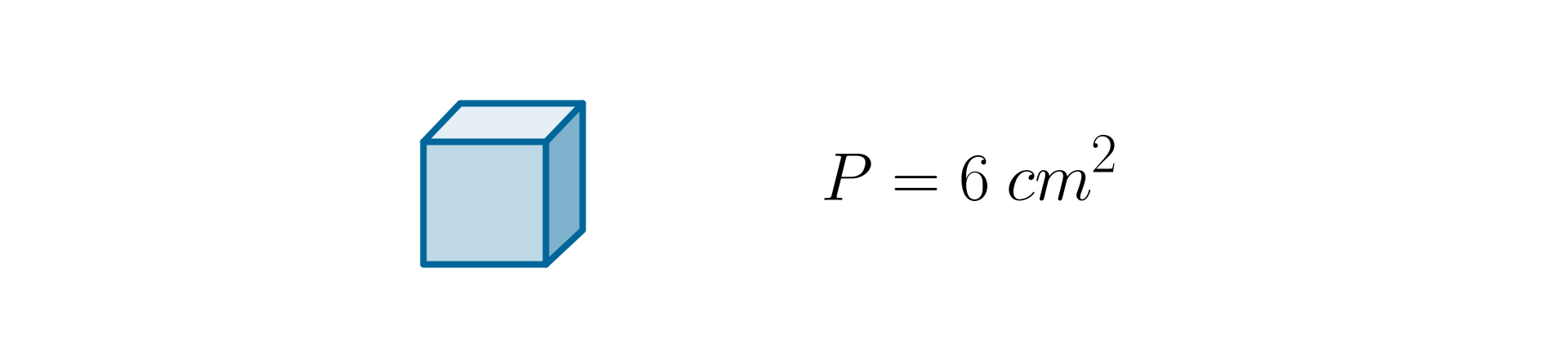
Jeżeli połączymy kwadratowe ściany dwóch takich sześcianów, otrzymamy graniastosłup o polu powierzchni .

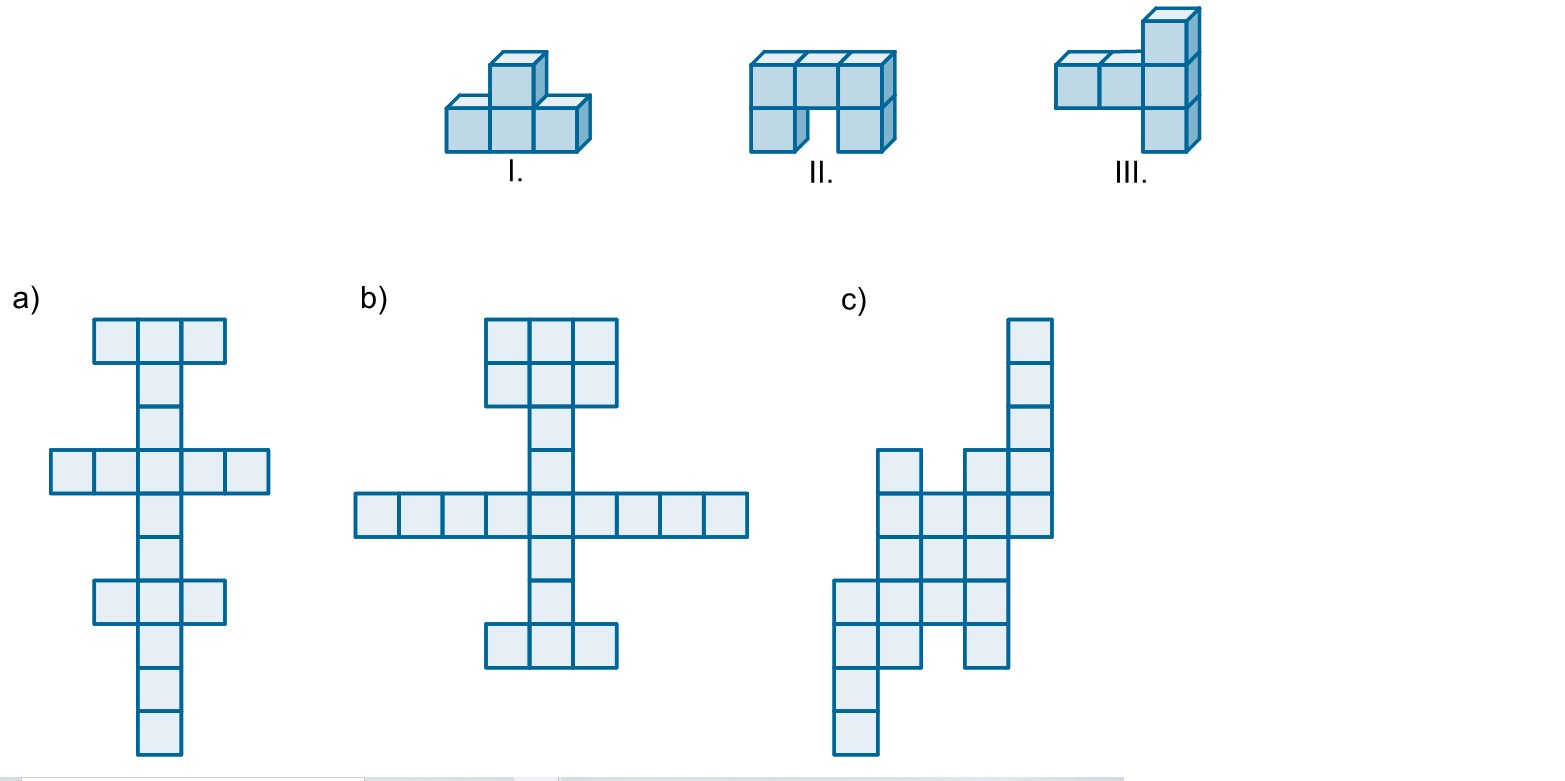
Gdy połączymy trzy sześciany, przykładając do siebie ich ściany, będziemy mogli otrzymamy dwie różne bryły.

Zaznacz bryły o polu powierzchni równej .
- 161442
- 161441
- 161443
- 161444




Bryły przedstawione na rysunku zbudowane są z pięciu jednakowych sześcianów o krawędzi długości . Wyznacz pola powierzchni tych brył.

Podaj przykłady przedmiotów, które są w kształcie prostopadłościanów lub sześcianów.
Bryła przedstawiona na rysunku zbudowana jest z sześciu jednakowych sześcianów o krawędzi długości . Wyznacz pola powierzchni tych brył.

Opisz etapy konstrukcji dowolnego modelu bryły złożonego z pięciu sześcianu o krawędzi długości .
Na rysunku przedstawiono bryły oraz ich siatki.
Siatka stożka składa się z powierzchni bocznej, która jest częścią koła i podstawy.

Rysunki przedstawiają powierzchnie boczne stożków. Są to części kół, o równych promieniach. Uporządkuj je w kolejności od powierzchni bocznej stożka o najmniejszym promieniu podstawy do powierzchni bocznej stożka o największym promieniu podstawy.

Rysunek przedstawia powierzchnie boczne dwóch stożków, przy czym promienie kół, z których wycięto obie figury mają równe promienie. Który ze stożków ma dłuższą wysokość?

Zapoznaj się z poniższym apletem i wykonaj zadanie.
Wyobraź sobie ostrosłup, którego podstawą jest sześciokąt foremny, a jego wysokość jest dwa razy dłuższa niż krawędź podstawy.
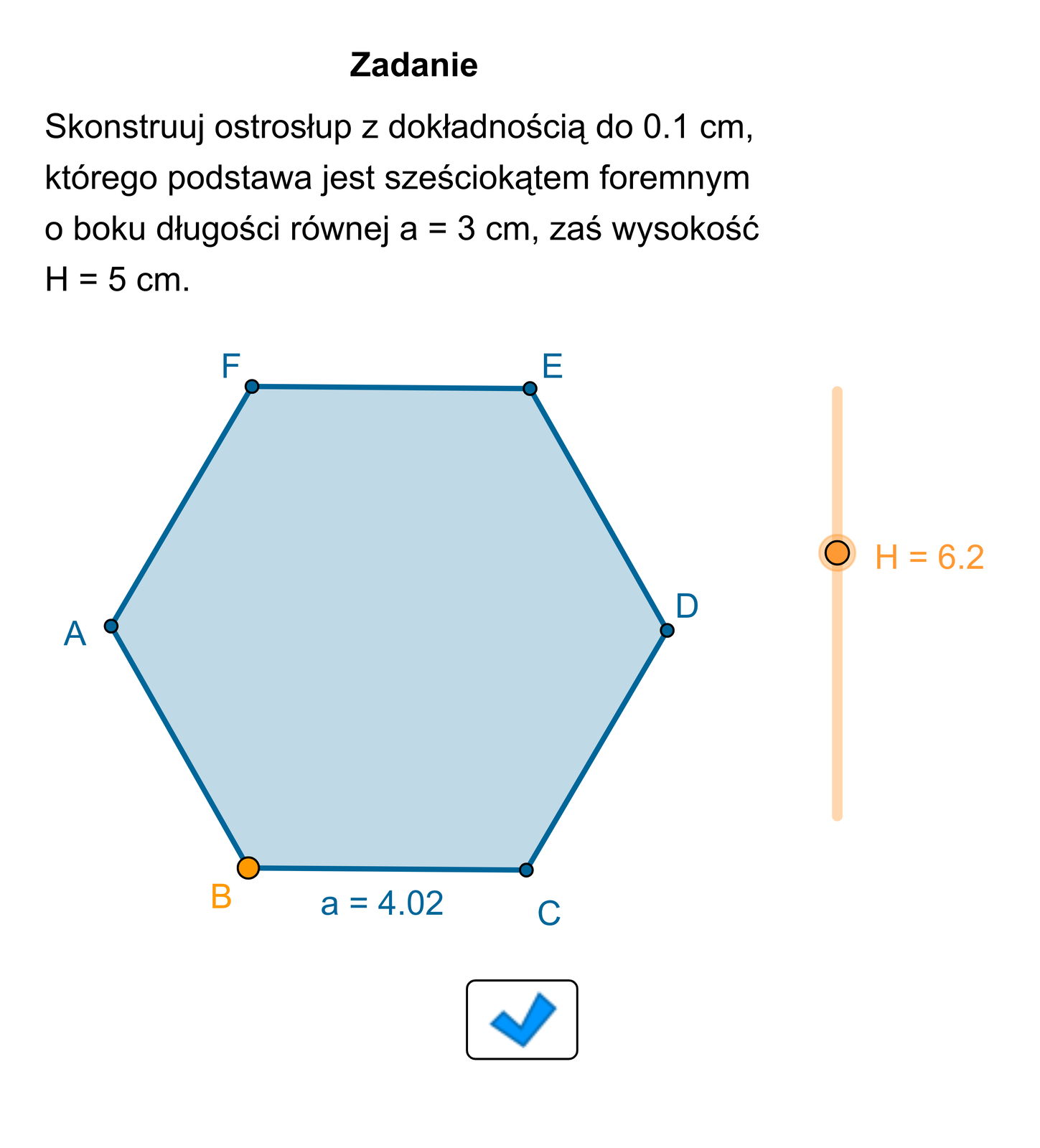
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DvQF1LucA
Zapoznaj się z poniższym apletem i wykonaj zadanie.
Wyobraź sobie graniastosłup, którego podstawą jest trapez równoramienny, w którym dłuższa podstawa jest trzykrotnością krótszej. Wysokość tego graniastosłupa jest równa długości dłuższej podstawy trapezu.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DvQF1LucA
Zapoznaj się z poniższym apletem i wykonaj zadanie.
Wyobraź sobie walec, w którym jego promień i wysokość mają tę samą długość.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DvQF1LucA
Zapoznaj się z poniższym apletem i wykonaj zadanie.
Wyobraź sobie stożek, w którym promień jest trzy razy krótszy niż jego wysokość.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DvQF1LucA
Zapoznaj się z poniższą infografiką, w której znajdziesz wszystkie najpotrzebniejsze wzory używane w geometrii przestrzennej.
Powtórz i utrwal sobie najpotrzebniejsze wzory, które są używane w geometrii przestrzennej.
Graniastosłupy
Wzór na pole powierzchni całkowitej graniastosłupa:
- pole podstawy graniastosłupa
- pole powierzchni bocznej (suma pól wszystkich ścian bocznych graniastosłupa)
Wzór na objętość graniastosłupa:
- pole podstawy graniastosłupa
- wysokość graniastosłupaProstopadłościan to graniastosłup, którego wszystkie ściany są prostokątami, oraz wszystkie ściany boczne są prostopadłe do podstaw.
Wzór na pole powierzchni całkowitej:
Wzór na objętość:
Wzór na przekątną bryły:
gdzie:
, , – długości krawędzi prostopadłościanuSześcian to prostopadłościan, którego wszystkie krawędzie są równej długości.
Wzór na pole powierzchni całkowitej:
Wzór na objętość:
Wzór na przekątną bryły:
gdzie:
– długość krawędzi sześcianu
Ostrosłupy
Wzór na pole powierzchni całkowitej ostrosłupa:
- pole podstawy ostrosłupa
- pole powierzchni bocznej (suma pól wszystkich ścian bocznych ostrosłupa)
Wzór na objętość ostrosłupa:
- pole podstawy ostrosłupa
- wysokość ostrosłupaOstrosłup prawidłowy trójkątny, to ostrosłup, który ma w podstawie trójkąt równoboczny.
Wzór na pole powierzchni całkowitej:
Wzór na objętość:
gdzie:
– długość krawędzi podstawy ostrosłupa
(małe) – wysokość scianu bocznej ostrosłupa
(duże) – wysokość ostrosłupaOstrosłup prawidłowy czworokątny, to ostrosłup, który ma w podstawie kwadrat.
Wzór na pole powierzchni całkowitej:
Wzór na objętość:
gdzie:
– długość krawędzi podstawy ostrosłupa
(małe) – wysokość scianu bocznej ostrosłupa
(duże) – wysokość ostrosłupaCzworościan foremny, to ostrosłup, który ma w podstawie oraz ścianach bocznych trójkąty równoboczne.
Wzór na pole powierzchni całkowitej:
Wzór na objętość:
gdzie:
– długość krawędzi ostrosłupa
Bryły obrotowe
Kula jest bryłą obrotową powstałą przez obrót półkola wokół prostej zawartej w jego średnicy.
Wzór na pole powierzchni :
Wzór na objętość:
gdzie:
– promień kuliStożek to bryła przestrzenna, która powstaje przez obrót trójkąta prostokątnego wokół jednej z przyprostokątnych.
Wzór na pole podstawy :
Wzór na pole boczne :
Wzór na pole powierzchni całkowitej :
Wzór na objętość :
gdzie:
– promień podstawy stożka
– tworząca stożka
– wysokość stożkaWalec to bryła przestrzenna, która powstaje przez obrót prostokąta wokół jednego z boków.
Wzór na pole podstawy :
Wzór na pole boczne :
Wzór na pole powierzchni całkowitej :
Wzór na objętość :
gdzie:
– promień podstawy walca
– tworząca walca
– wysokość walca
Geometria przestrzenna - powtórzenie