Graniastosłup prosty i jego własności. Związki miarowe w graniastosłupach
Materiał ten poświęcony jest graniastosłupowi prostemu oraz jego własnościom. Zawarta jest w nim podstawowa definicja takiego graniastosłupa, własności dotyczące jego kątów i przekrojów, a także przykłady, pokazujące jak wykorzystać różne własności tej bryły w zadaniach.
Graniastosłup prosty to taki wielościan, którego dwie przystające ściany (podstawy graniastosłupa) są położone w równoległych płaszczyznach, a pozostałe ściany są prostokątami.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Kliknij w lukę, aby wyświetlić listę rozwijalną i wybierz poprawną odpowiedź. Graniastosłup prosty trójkątny posiada 1. , 2. , 3. , 4. , 5. , 6. wierzchołków.W graniastosłupie prostym pięciokątnym jest 1. , 2. , 3. , 4. , 5. , 6. ścian.Graniastosłup prosty sześciokątny posiada 1. , 2. , 3. , 4. , 5. , 6. krawędzi.W graniastosłupie prostym ośmiokątnym jest 1. , 2. , 3. , 4. , 5. , 6. ścian.Graniastosłup prosty dziesięciokątny posiada 1. , 2. , 3. , 4. , 5. , 6. wierzchołków.Graniastosłup prosty czworokątny posiada 1. , 2. , 3. , 4. , 5. , 6. krawędzi.

Film dostępny pod adresem /preview/resource/RlS5Agww86Rb9
Animacja przedstawia różnego rodzaju figury przestrzenne.

Film dostępny pod adresem /preview/resource/RoqsbpwWYdxko
Animacja pokazuje przykłady trzech figur przestrzennych, które są graniastosłupami o różnych podstawach.
Podstawą graniastosłupa może być np. trójkąt, czworokąt i sześciokąt.

Jeżeli podstawą graniastosłupa jest wielokąt foremny (trójkąt równoboczny, kwadrat, pięciokąt foremny itd.), to mówimy, że taki graniastosłup jest prawidłowy.


Film dostępny pod adresem /preview/resource/R1JvgbMkvRaLK
Animacja przedstawia w jaki sposób możemy narysować graniastosłup prosty.
Graniastosłup, którego podstawą jest prostokąt, nazywać będziemy prostopadłościanem.
Własności prostopadłościanu
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
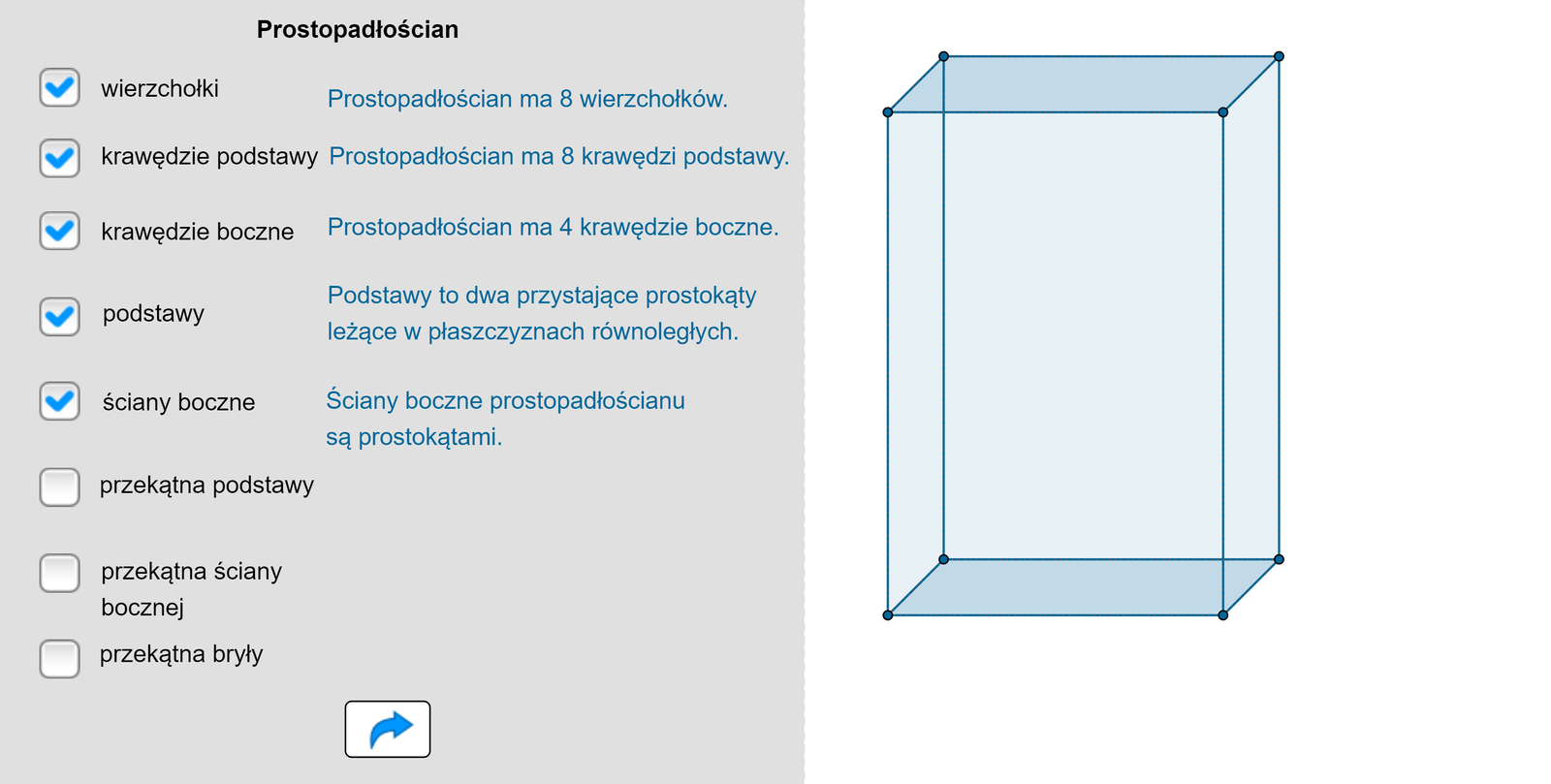
Opiszemy dokładnie własności prostopadłościanu, czyli graniastosłupa, którego podstawą jest prostokąt.
Prostopadłościan posiada wierzchołków i krawędzi podstawy. Krawędzi bocznych ma .
Podstawy prostopadłościanu to dwa przystające prostokąty leżące w płaszczyznach równoległych. Ściany boczne prostopadłościanu są prostokątami.
Każda z podstaw prostopadłościanu ma dwie przekątne. Każda ściana boczna również posiada dwie przekątne. Prostopadłościan ma cztery przekątne, każdą wychodzącą z jednego z czterech wierzchołków podstawy prostopadłościanu.
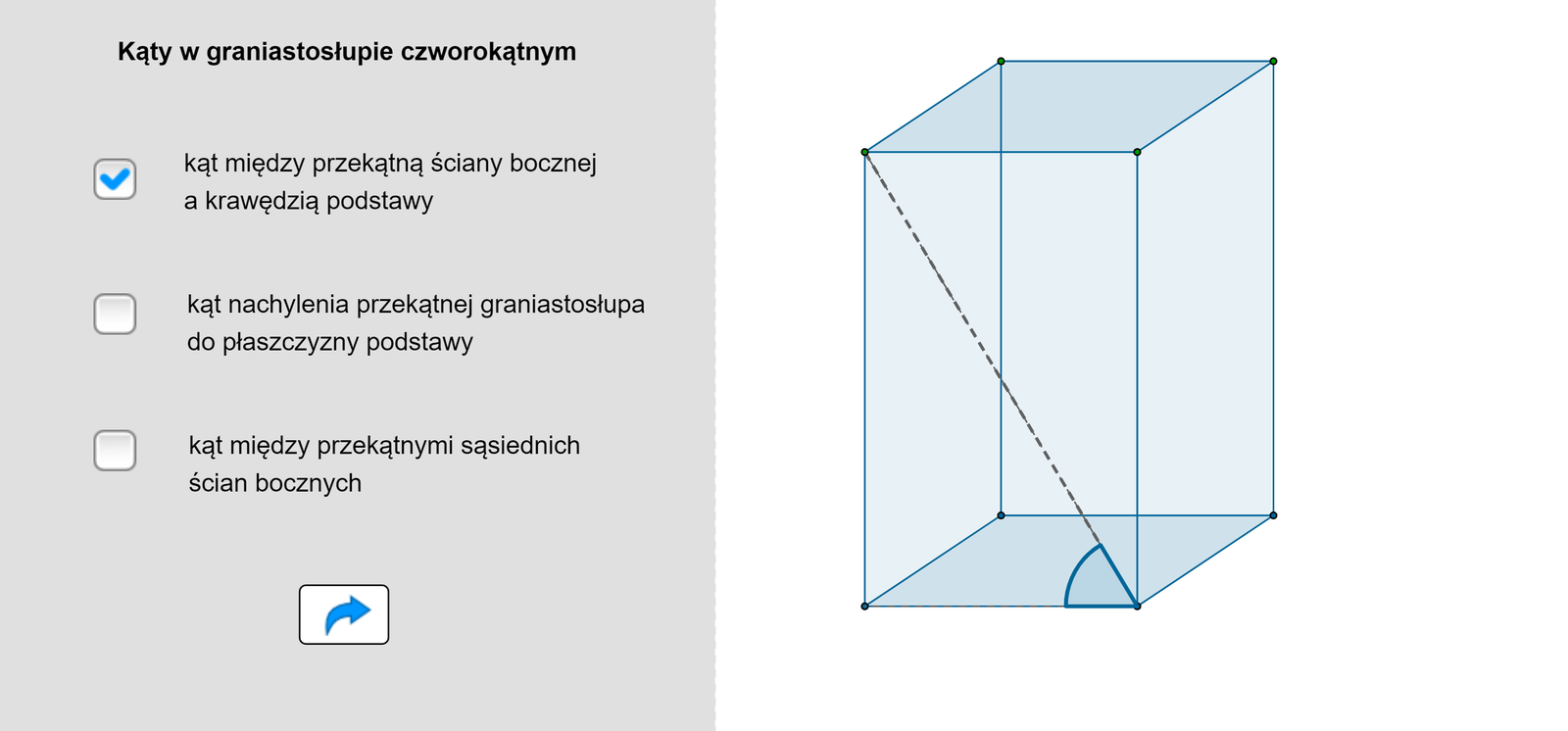
Kąty w prostopadłościanie
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Film dostępny pod adresem /preview/resource/R10gQdIF4aFwr
Animacja przedstawia jakie bryły możemy nazywać prostopadłościanami.
Przekroje w prostopadłościanie
Sześcian to taki prostopadłościan, którego wszystkie ściany są kwadratami.
Krawędź sześcianu jest równa . Obliczymy długość przekątnej sześcianu.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Krawędź sześcianu jest równa . Obliczymy długość przekątnej sześcianu.
Rozwiązanie:
Obliczamy długość przekątnej sześcianu o krawędzi równej . Przekątną podsatwy jest przekątna kwadratu o boku , czyli
.
Przekątna sześcianu jest przeciwprostokątną w trójkącie prostokątnym, którego jedną przeciwprostokątną jest przekątna kwadratu, a drugą długość krawędzi bocznej. Na podstawie twierdzenia Pitagorasa otrzymujemy
.
Długość przekątnej sześcianu jest równa .
Zauważ, że jeśli podobne obliczenia wykonamy dla dowolnego sześcianu o krawędzi , to otrzymamy wzór na przekątne sześcianu.
Przekątna sześcianu o krawędzi jest równa

Siatka sześcianu

Film dostępny pod adresem /preview/resource/R1VZTid03uHRO
Animacja 3D pokazuje leżące na stole kostki do gry. Kreślone są krawędzie jednej kostki – powstaje sześcian. Dwa jednakowe sześciany rozkładają się na dwie różne siatki sześcianu.

Film dostępny pod adresem /preview/resource/R1Zciw8RcK6Oy
Animacja 3D pokazuje dwie różne siatki sześcianu, które składają się w jednakowe sześciany. Sześcian zamienia się w kostkę do gry, która leży z innymi kostkami na stole.
Sześcian jest szczególnym przypadkiem prostopadłościanu, którego wszystkie ściany są identyczne i są kwadratami.
Sześcian możemy rozłożyć na płasko, uzyskując siatkę składającą się sześciu takich samych kwadratów. Tak samo jak w przypadku prostopadłościanu, układ siatki nie jest przypadkowy. Nie każde sześć identycznych kwadratów może utworzyć sześcian. Przykłady konstrukcji siatek przedstawimy poniżej. Dla wygody ponumerujemy ściany boczne sześcianu liczbami od 1 do 4.
Weźmy górną podstawę bryły. Do jej dolnego boku przylega ściana 1 . Po prawej stronie tej ściany znajdują się kolejno przylegające ściany 2, 3 i 4. Do dolnego boku ściany 1 przylega swoim górnym bokiem podstawa dolna.
Drugim przykładem siatki może być siatka tej samej bryły, której opis zaczniemy od górnej podstawy. Do jej prawego boku przylega ściana 1, do lewego boku przylega ściana 2, do górnego boku przylega ściana 3, a do dolnego boku przylega ściana 4 .Do dolnego boku ściany 4 przylega dolna podstawa.
Siatka prostopadłościanu

Film dostępny pod adresem /preview/resource/RSH3INKYcbX0g
Animacja 3D pokazuje kolumny. Kreślone są krawędzie jednej kolumny – powstaje prostopadłościan. Dwa jednakowe prostopadłościany rozkładają się na dwie różne siatki prostopadłościanu.

Film dostępny pod adresem /preview/resource/REA6GdjI8ytqP
Animacja 3D pokazuje dwie różne siatki prostopadłościanu, które składają się w jednakowe prostopadłościany. Prostopadłościan zmienia się w kolumnę, która stoi obok innych kolumn.
Prostopadłościan jest trójwymiarową bryłą przypominającą klocek. Składa się on z czterech prostokątnych ścian połączonych ze sobą bokami dokładnie w taki sam sposób jak na przykład ściany pokoju. Bryła ta posiada również dwie podstawy: górną i dolną, które w naszym porównaniu byłyby sufitem i podłogą pokoju. Prostopadłościan możemy rozłożyć na płasko, uzyskując siatkę składającą się z sześciu figur: dwóch par identycznych prostokątów, czyli przeciwległych ścian oraz dwóch identycznych prostokątów będących podstawami. Oznacza to, że nie wszystkie ściany bryły muszą być identyczne. Prostopadłościan może bowiem być „spłaszczony”.
Układ siatki nie jest przypadkowy. Nie każde trzy pary identycznych prostokątów mogą utworzyć prostopadłościan. Przykłady konstrukcji siatek przedstawimy poniżej. Dla wygody określmy, że nasz prostopadłościan składa się z pary identycznych ścian A, pary identycznych ścian B oraz podstawy górnej i dolnej. Oczywiście ściany A i B mogą być w szczególności identyczne, jeśli tylko podstawy są kwadratami.
Weźmy górną podstawę bryły. Do jej dolnego boku przylega ściana A. Po bokach tej ściany znajdują przylegające do niej ściany B. Do dolnego boku ściany A przylega swoim górnym bokiem podstawa dolna, a do dolnego boku dolnej podstawy przylega ściana A.
Drugim przykładem siatki może być siatka tej samej bryły, której opis zaczniemy od ściany B. Do jej prawego boku przylega ściana A. Do prawego boku ściany A przylega druga ściana B. Do prawego boku drugiej ściany B przylega druga ściana A, do której górnego i dolnego boku przylegają obie podstawy.
Siatka graniastosłupa sześciokątnego

Film dostępny pod adresem /preview/resource/RAtgT0raD067M
Animacja 3D pokazuje nakrętki na śruby. Kreślone są krawędzie jednej nakrętki – powstaje graniastosłup o podstawie sześciokąta foremnego. Dwa jednakowe graniastosłupy rozkładają się na dwie różne siatki graniastosłupa.

Film dostępny pod adresem /preview/resource/R1Q3GHU0RbYTp
Animacja 3D pokazuje dwie różne siatki graniastosłupa, które składają się w jednakowe graniastosłupy. Graniastosłup zamienia się w nakrętkę leżącą między nakrętkami.
Graniastosłup sześciokątny jest trójwymiarową bryłą, która składa się z sześciu prostokątnych ścian połączonych ze sobą bokami. Bryła ta posiada również dwie podstawy: górną i dolną. Taki graniastosłup możemy rozłożyć na płasko, uzyskując siatkę składającą się z ośmiu figur: dwóch identycznych sześciokątów, czyli przeciwległych podstaw oraz sześciu identycznych prostokątów, będących ścianami bocznymi.
Układ siatki nie jest przypadkowy. Nie z każdych dwóch sześciokątów i sześciu prostokątów możemy ułożyć siatkę graniastosłupa sześciokątnego. Przykłady konstrukcji siatek przedstawimy poniżej. Dla wygody ponumerujemy ściany boczne sześcianu liczbami od 1 do 6.
Weźmy górną podstawę bryły. Do jej dolnego boku przylega ściana 1 . Po prawej stronie tej ściany znajdują się kolejno przylegające ściany 2, 3, 4, 5 i 6. Do dolnego boku ściany 1 przylega swoim górnym bokiem podstawa dolna.
Drugim przykładem siatki może być siatka tej samej bryły, której opis zaczniemy od górnej podstawy. Do każdego boku podstawy przylega jedna ściana boczna, a do dolnego boku dowolnej ze ścian przylega dolna podstawa.
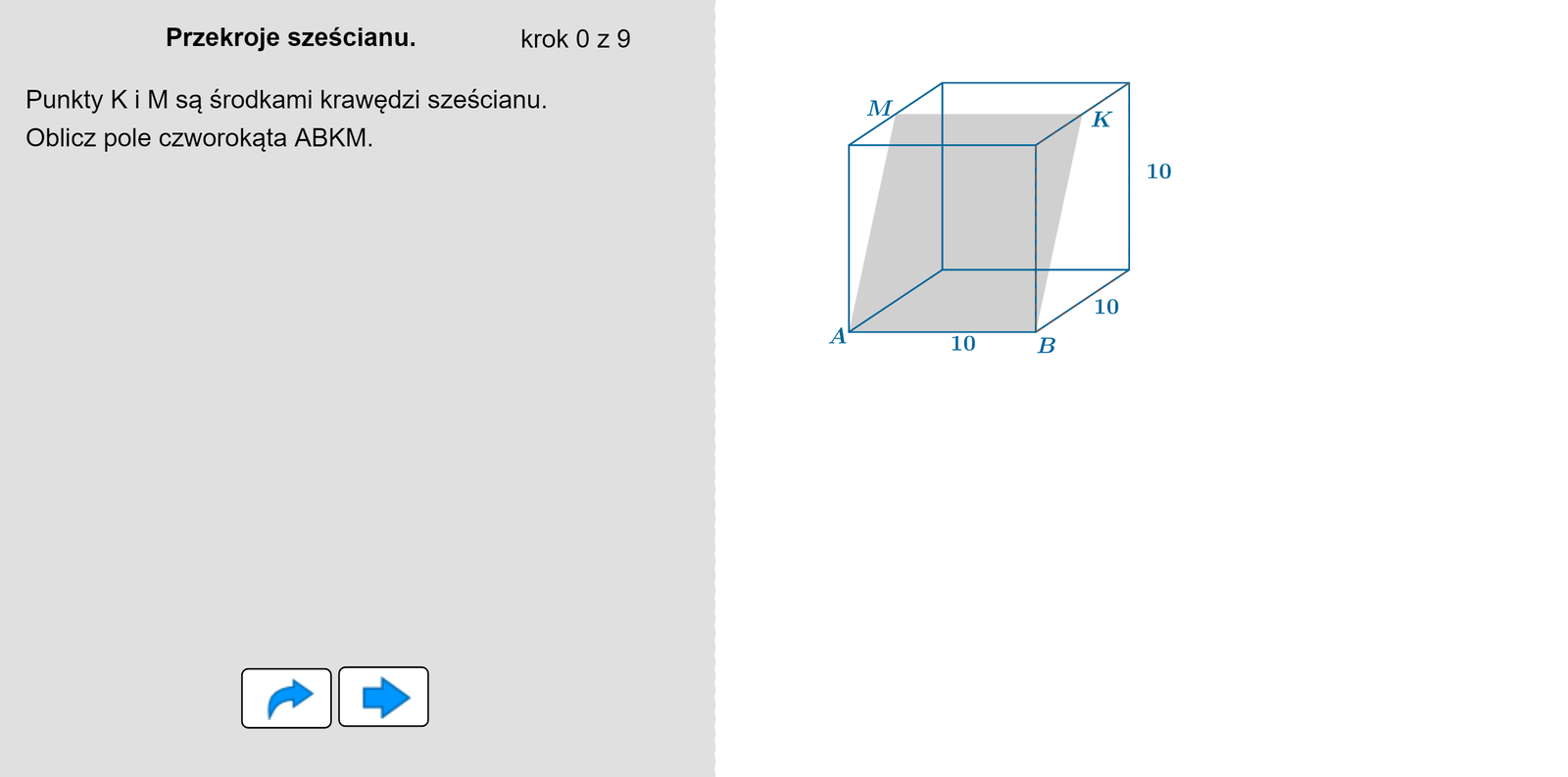
Punkty i są środkami krawędzi sześcianu jak na rysunku. Obliczymy pole powierzchni czworokąta .

Rozwiązanie
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Punkty i są środkami krawędzi górnej podsatwy sześcianu. Obliczamy pole powierzchni czworokąta , gdzie i są wierzchołkami dolnej podstawy.
Rozwiązanie:
Odcinki i leża na płaszczyznach równoległych i są sobie równe. Podobnie odcinki oraz . Ponadto odcinek leży na płaszczyźnie prostopadłej do podstawy sześcianu i jest postopadły do krawędzi . Wynika z tego , że czworokąt jest prostokątem. Obliczymy długości boków prostokąta .
Bok jest krawędzią sześcianu, czyli .
Bok jest przeciwprostokątną w trójkącie prostokątnym i oznaczamy go jako . Z twierdzenia Pitagorasa otrzymujemy:
,
,
.
Pole prostokąta jest równe
.
Pole powierzchni całkowitej i objętość graniastosłupa.
Pole powierzchni całkowitej graniastosłupa jest równe
gdzie oznacza pole podstawy graniastosłupa, a – pole powierzchni bocznej.
W szczególności pole całkowite
prostopadłościanu o krawędziach , , jest równe
sześcianu o krawędzi jest równe
graniastosłupa prawidłowego czworokątnego o krawędzi podstawy i wysokości jest równe
Objętość graniastosłupa jest równa
gdzie oznacza pole podstawy graniastosłupa, a – wysokość bryły.
W szczególności objętość
prostopadłościanu o krawędziach , , jest równa
sześcianu o krawędzi jest równa
graniastosłupa prawidłowego czworokątnego o krawędzi podstawy i wysokości jest równa
Przekątna podstawy sześcianu ma długość . Obliczymy pole powierzchni całkowitej i objętość sześcianu.

Przekątna kwadratu jest równa , zatem otrzymujemy równanie , czyli .
Wynika z tego, że objętość sześcianu jest równa
a pole powierzchni całkowitej
W graniastosłupie prawidłowym czworokątnym przekątna podstawy ma długość , a przekątna ściany bocznej . Obliczymy pole powierzchni całkowitej graniastosłupa.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
W graniastosłupie prawidłowym czworokątnym przekątna podstawy ma długość , a przekątna ściany bocznej . Obliczymy pole powierzchni całkowitej.
Rozwiązanie:
Przypomnijmy wzór na pole powierzchni całkowitej graniastosłupa , czyli .
Przekątna podstawy to przekątna kwadratu o boku .
Przekątna kwadratu jest równa , zatem , czyli .
Przekątna ściany bocznej jest przeciprostokątną w trójkącie prostokatnym, którego przyprostokątne to krawędzi podsatwy i krawędź boczna, czyli wysokość . Z twierdzenia Pitagorasa otrzymujemy :
, czyli .
Po wstawieniu do wzoru na pole powierzchni całkowitej otrzymujemy
,
.
Obliczymy pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość , a przekątna graniastosłupa jest razy dłuższa od przekątnej podstawy.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Obliczymy pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego, którego krawędź podstawy ma długość , a przekątna graniastosłupa jest razy dłuższa niż przekątna podstawy.
Rozwiązanie:
Przypomnijmy wzór na pole powierzchni całkowitej graniastosłupa , czyli .
Podstawą bryły jest kwadrat o boku , czyli .
Przekątna podstawy to przekątna kwadratu o boku , czyli .
Przekątna bryły jest razy dłuższa od przekątne podstawy. Wysokośc bryły jest przyprostokątną w trójkącie prostokątnym w którym drugą przyprosotkątną jest przekątna podsatwy, a przeciwprostokątną jest przekątna bryły. Z twierdzenia Pitagorasa otrzymujemy:
,
, czyli .
Po wsatwieniu do wzoru na pole powierzchni całkowitej otrzymujemy:
,
.
Przekątna prostopadłościanu ma długość i jest nachylona do podstawy pod kątem . Pole podstawy prostopadłościanu jest równe . Obliczymy objętość bryły.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Przekątna prostopadłościanu ma długość i jest nachylona do płaszczyzny podstawy pod katem . Pole podstawy prostopadłościanu jest równe . Obliczymy objętość bryły.
Rozwiązanie:
Podsatwą prostopadłościanu jest prostokąt o polu równym .
Kąt zwarty między przekątna prostopadłościanu i przekątną podstawy jest równy .
Powstaje trójkąt prostokątny, którego przyprostokątne to odpowiednią przekątna podstawy i wysokość prostopadłościanu, natomiast przeciwprostokątna to przekątna bryły. Z definicji funkcji trygonometrycznych w trójkącie prostokątnym otrzymujemy:
, czyli .
Wynika z tego, że .
Objętość prostopadłościanu jest równa zatem .
Podstawą graniastosłupa jest trójkąt równoboczny o polu . Przekątna ściany bocznej jest nachylona do krawędzi podstawy pod kątem . Obliczymy pole powierzchni całkowitej bryły.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Obliczymy pole powierzchni całkowitej bryły.
Rozwiązanie:
Podstawą graniastosłupa jest trójkąt równoboczny. Pole trójkąta równobocznego jest równe
, czyli .
Wynika z tego, że .
Ściana boczna graniastosłupa jest prostokątem, którego przekątna jest nachylona do boku pod kątem .
Z definicji funkcji trygonometrycznych w trójkącie prostokątnym otrzymujemy , czyli .
Wynika z tego, że .
Zatem pole ściany bocznej jest równe .
Pole powierzchni całkowitej tego graniastosłupa jest równe , czyli .
Objętość graniastosłupa o podstawie kwadratu jest równa . Przekątna ściany bocznej jest nachylona do płaszczyzny podstawy pod kątem . Obliczymy pole powierzchni całkowitej graniastosłupa.

Pole powierzchni całkowitej tego graniastosłupa jest równe – zatem do jego obliczenia będzie potrzebna długość krawędzi podstawy i wysokość bryły.
W trójkącie prostokątnym mamy:
zatem
czyli
Objętość graniastosłupa jest równa , czyli .
Wstawiając wyznaczoną wcześniej wartość , otrzymamy
, czyli . Wynika z tego, że oraz
Zatem pole powierzchni całkowitej jest równe:
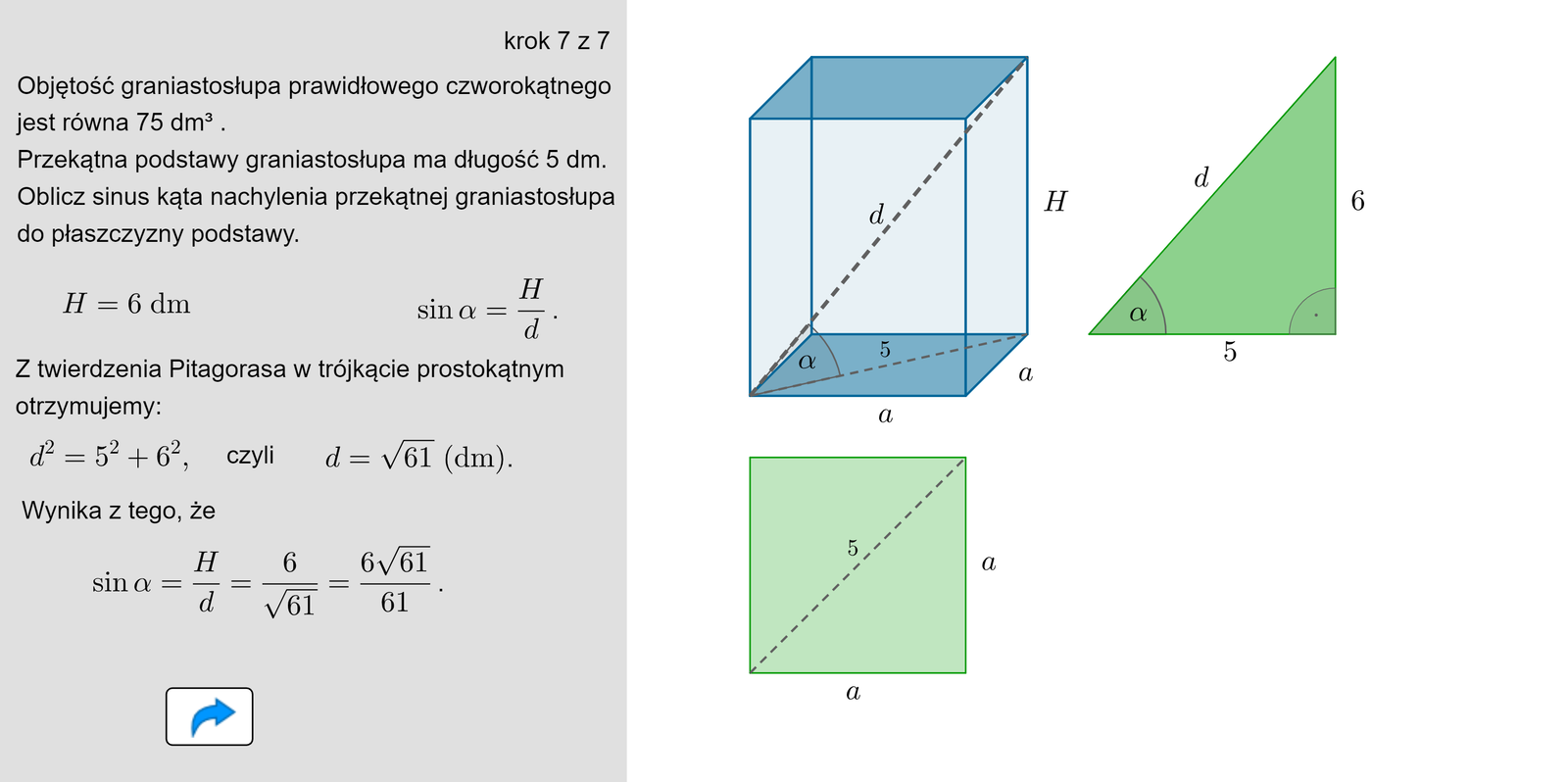
Objętość graniastosłupa prawidłowego czworokątnego jest równa . Przekątna podstawy graniastosłupa ma długość . Oblicz sinus kąta nachylenia przekątnej graniastosłupa do płaszczyzny podstawy.
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PK0bvQUSB
Objętość graniastosłupa prawidłowego czworokątnego jest równa . przekątna podsatwy graniastoslupa ma długość . Oblicz sinus kąta nachylenia przekątnej graniastosłupa do płaszczyzny podstawy.
Rozwiązanie:
W podanym graniastosłupie prawidłowym czworokątnym możemy wyznaczyć trójkąt prostokątny, którego przyprostokątne to przekątna podstawy oraz wysokość bryły, natomiast przeciwprostokątna to przekątna graniastosłupa. Z definicji funkcji trygonometrycznych w trójkącie prostokątnym wiemy, że sinus kąta zwartego między przekątną graniastosłupa a przekątną podstawy jest równy :
.
Z treści zadania wynika, że
, czyli .
Podstawą graniastosłupa jest kwadrat, którego przekątna jest równa . Zatem
, czyli .
Po wstawieniu do wzoru na objętość graniastosłupa otrzymujemy:
, czyli .
Z twierdzenia Pitagorasa w trójkącie prostokątnym otrzymujemy:
, czyli .
Wynika z tego, że
.
Pole powierzchni całkowitej graniastosłupa prawidłowego czworokątnego jest równe , a suma długości wszystkich krawędzi jest równa . Oblicz objętość tego graniastosłupa.
Kliknij w lukę, aby wyświetlić listę rozwijalną i wybierz poprawną odpowiedź. Odpowiedź: Objętość tego prostopadłościanu wynosi 1. , 2. , 3. , 4. .
Uzupełnij luki w odpowiedzi. Kliknij w nie, aby rozwinąć listę, a następnie wybierz poprawną liczbę. Odpowiedź: Pole powierzchni całkowitej tego sześcianu wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , a objętość tego sześcianu wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
Pole powierzchni całkowitej sześcianu jest równe . Oblicz pole trójkąta .

Uzupełnij lukę w odpowiedzi. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną liczbę. Odpowiedź: Pole powierzchni całkowitej tego sześcianu wynosi 1. , 2. , 3. , 4. , 5. , 6. , a jego objętość to 1. , 2. , 3. , 4. , 5. , 6. .
Uzupełnij lukę w odpowiedzi. Kliknij w nią, aby rozwinąć listę, a następnie wybierz poprawną liczbę. Odpowiedź: W sześcianie cosinus tego kąta nachylenia wynosi 1. , 2. , 3. , 4. , 5. .