Metoda przeciwnych współczynników rozwiązywania układów równań
Metoda przeciwnych współczynników polega na tym, aby po dodaniu lub odjęciu równań stronami wyeliminować jedną z niewiadomych i otrzymać równanie pierwszego stopnia z jedną niewiadomą.
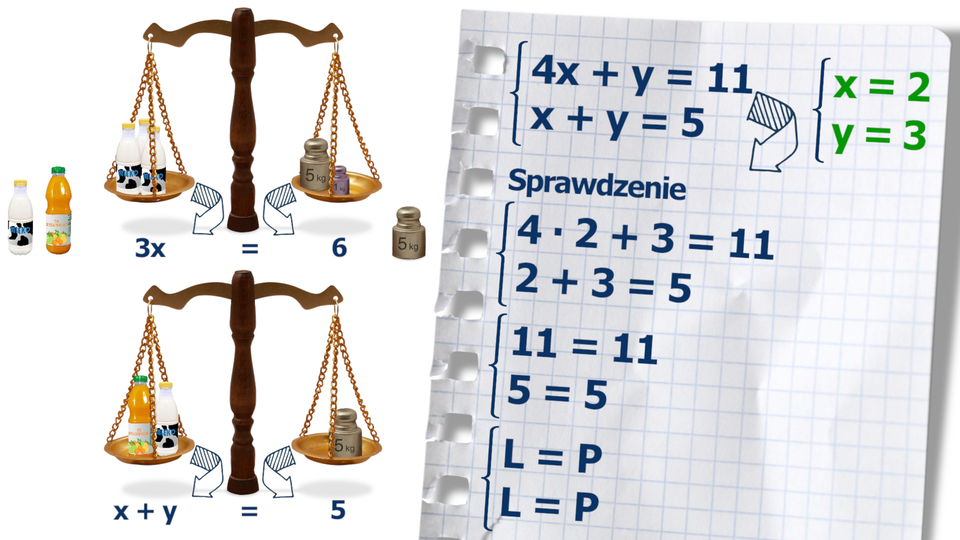
Film dostępny pod adresem /preview/resource/REzx4R1zgBzwR
Animacja przedstawia w jaki sposób możemy opisać różne przedmioty znajdujące się na wadze szalkowej w równowadze przy pomocy układów równań oraz w jaki sposób rozwiązać taki układ równań.
Omawiana metoda rozwiązywania układów równań nazywa się metodą przeciwnych współczynników, ponieważ gdy współczynniki przy wybranej niewiadomej są liczbami przeciwnymi, wystarczy dodać równania stronami w celu zredukowania jednej zmiennej i otrzymania równania z jedną niewiadomą.
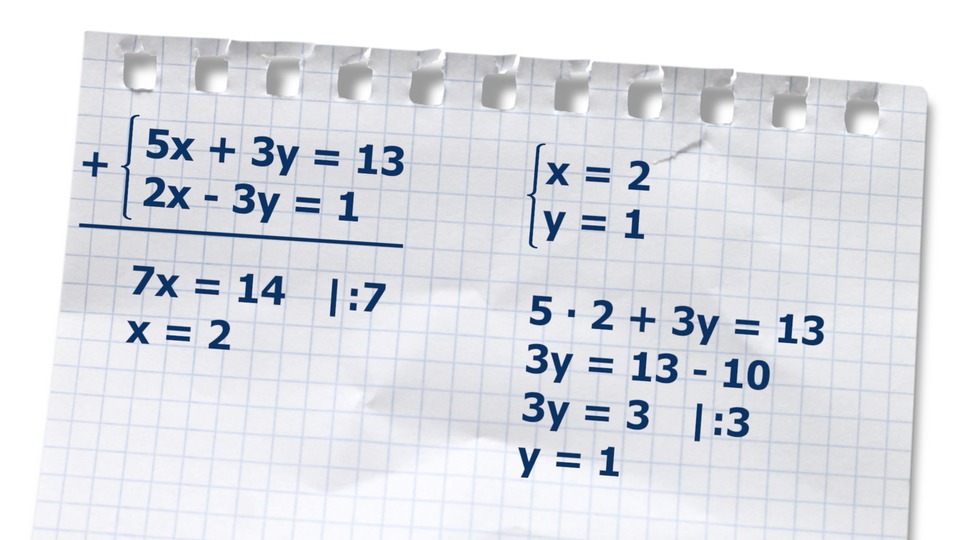
Film dostępny pod adresem /preview/resource/RvzDcmnZlnWXR
Animacja przedstawia przykładowe rozwiązanie pewnego układu równań metodą przeciwnych współczynników.
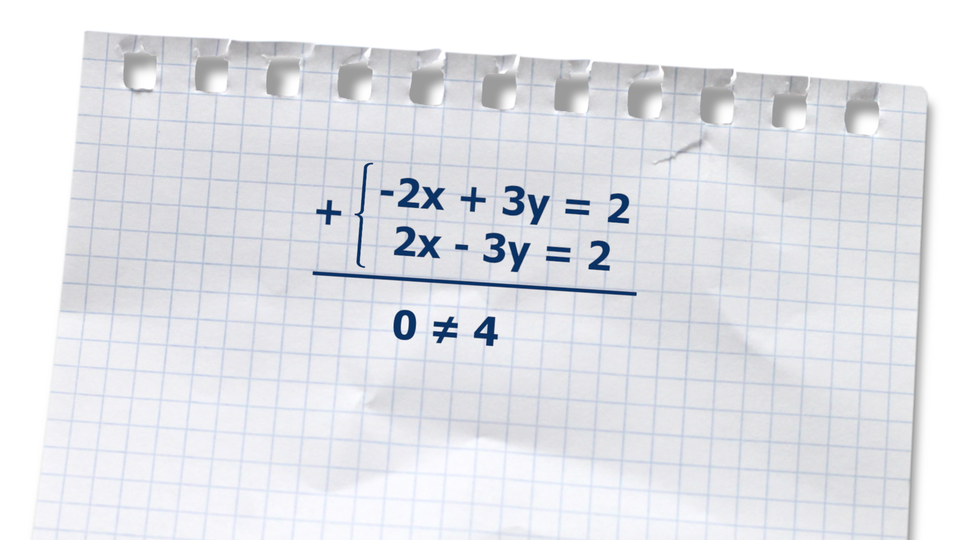
Film dostępny pod adresem /preview/resource/R1ecOykOJnB6D
Animacja przedstawia przykładowe rozwiązanie pewnego układu równań metodą przeciwnych współczynników.
Jeżeli, rozwiązując układ równań metodą przeciwnych współczynników, równanie, które otrzymaliśmy w wyniku dodawania równań stronami, okaże się równaniem sprzecznym, to układ równań nie ma rozwiązania, jest układem sprzecznym.
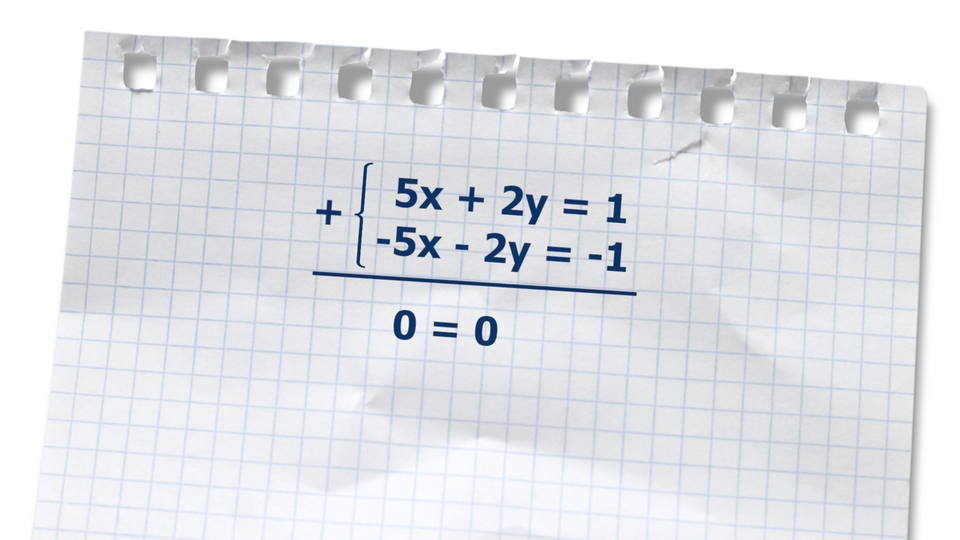
Film dostępny pod adresem /preview/resource/R1ZIilh8R1XFW
Animacja przedstawia przykładowe rozwiązanie pewnego układu równań metodą przeciwnych współczynników.
Jeżeli, rozwiązując układ równań metodą przeciwnych współczynników, równanie, które otrzymaliśmy w wyniku dodawania równań stronami, okaże się równaniem tożsamościowym, to układ równań ma nieskończenie wiele par liczb spełniających ten układ, czyli jest to układ nieoznaczony.
Nie zawsze współczynniki przy niewiadomych lub są liczbami przeciwnymi.
Czasami trzeba obie strony jednego z równań pomnożyć lub podzielić przez odpowiednią liczbę różną od zera, aby otrzymać przeciwne współczynniki przy wybranej niewiadomej.
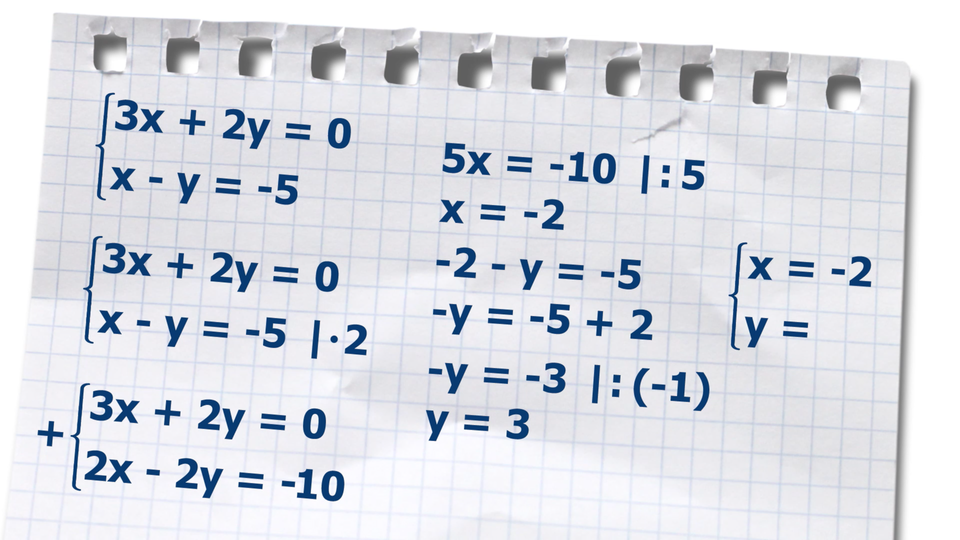
Film dostępny pod adresem /preview/resource/RCPXRiuhmjwsx
Animacja przedstawia przykładowe rozwiązanie pewnego układu równań metodą przeciwnych współczynników.
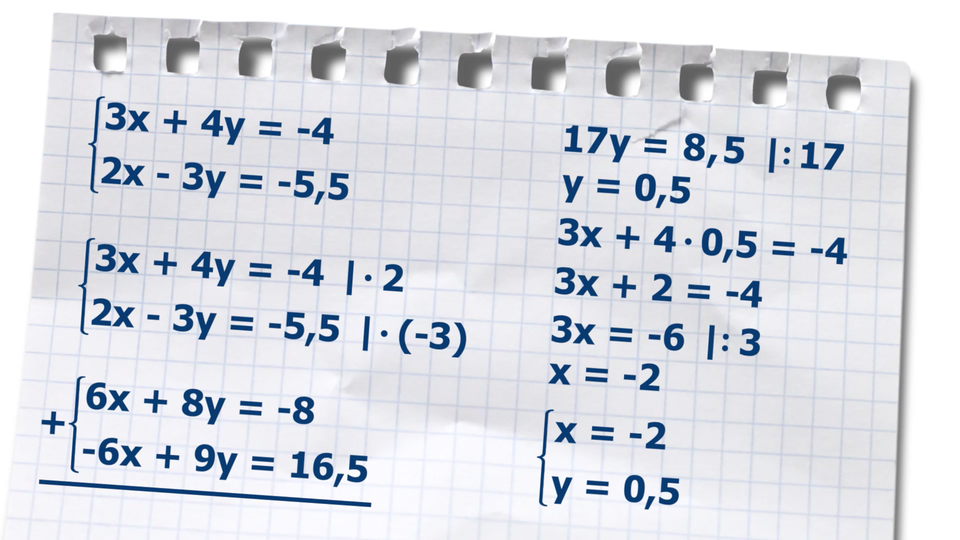
Film dostępny pod adresem /preview/resource/RaFIhTqtMtNdF
Animacja przedstawia przykładowe rozwiązanie pewnego układu równań metodą przeciwnych współczynników.
-
7 x = 10 -
7 x = 14 -
x = 2 -
7 y = 14
-
2 - 3 -
2 3 -
5 2 -
5 2
Etap 1.
Układ równań,
Pierwsze równanie
drugie równanie
koniec układu równań.
Etap 2.
Układ równań,
Pierwsze równanie 1.
drugie równanie
koniec układu równań.
Etap 3.
1.
Etap 4.
Przeciągnij i upuść tak, aby utworzyć kolejne etapy rozwiązania układu równań metodą przeciwnych współczynników.
1. Etap
2. Etap
{
3. Etap
................................................................................................................
4. Etap
Etap 1.
Układ równań,
Pierwsze równanie
drugie równanie
koniec układu równań.
Etap 2.
Układ równań,
pierwsze równanie 1.
drugie równanie 1.
koniec układu równań.
Etap 3.
1.
Etap 4.
1.
Przeciągnij i upuść tak, aby utworzyć kolejne etapy rozwiązania układu równań metodą przeciwnych współczynników.
1. Etap
2. Etap
..................................................................................................
..................................................................................................
3. Etap
..................................................................................................
4. Etap
..................................................................................................
Etap 1.
Układ równań,
Pierwsze równanie
drugie równanie
koniec układu równań.
Etap 2.
Układ równań,
pierwsze równanie
drugie równanie 1.
koniec układu równań.
Etap 3.
1.
Etap 4.
Etap 1.
Układ równań
pierwsze równanie
drugie równanie
koniec układu równań.
Etap 2.
Układ równań
pierwsze równanie 1.
drugie równanie
koniec układu równań.
Etap 3.
1.
Etap 4.
- nieoznaczony
- sprzeczny
- oznaczony
- oznaczony
- sprzeczny
- nieoznaczony
- sprzeczny
- nieoznaczony
- oznaczony
Zaznacz prawidłową odpowiedź. Możliwe odpowiedzi: 1.
-
x = 1 y = - 4 1 2 -
x = 1 y = - 2 1 2 -
x = 4 1 2 y = 1 -
x = - 1 y = - 2