Miejsca zerowe funkcji
Przyjrzyjmy się wykresowi zmian temperatury powietrza w pewnej miejscowości w marcu.

Z wykresu możemy odczytać, że temperatura powietrza w dniu marca była równa natomiast marca wynosiła C. Możemy też zadać pytanie: kiedy temperatura wynosiła C? Z wykresu odczytujemy, że temperaturę C odnotowano czterokrotnie: , , , marca.

Szczególną wartością temperatury powietrza jest C. W tej temperaturze woda przechodzi ze stanu stałego w ciekły lub na odwrót. Zadajmy sobie pytanie: kiedy w marcu, w tej miejscowości odnotowano temperaturę C? Z wykresu odczytujemy: , , marca. Przyjmijmy, że rysunek przedstawia wykres pewnej funkcji. Wtedy dla wartości tej funkcji wynoszą .
Każdy argument, dla którego funkcja przyjmuje wartość nazywamy miejscem zerowym tej funkcji.
Wykres przedstawia zmiany stanu konta klienta banku w pierwszych jedenastu dniach miesiąca.
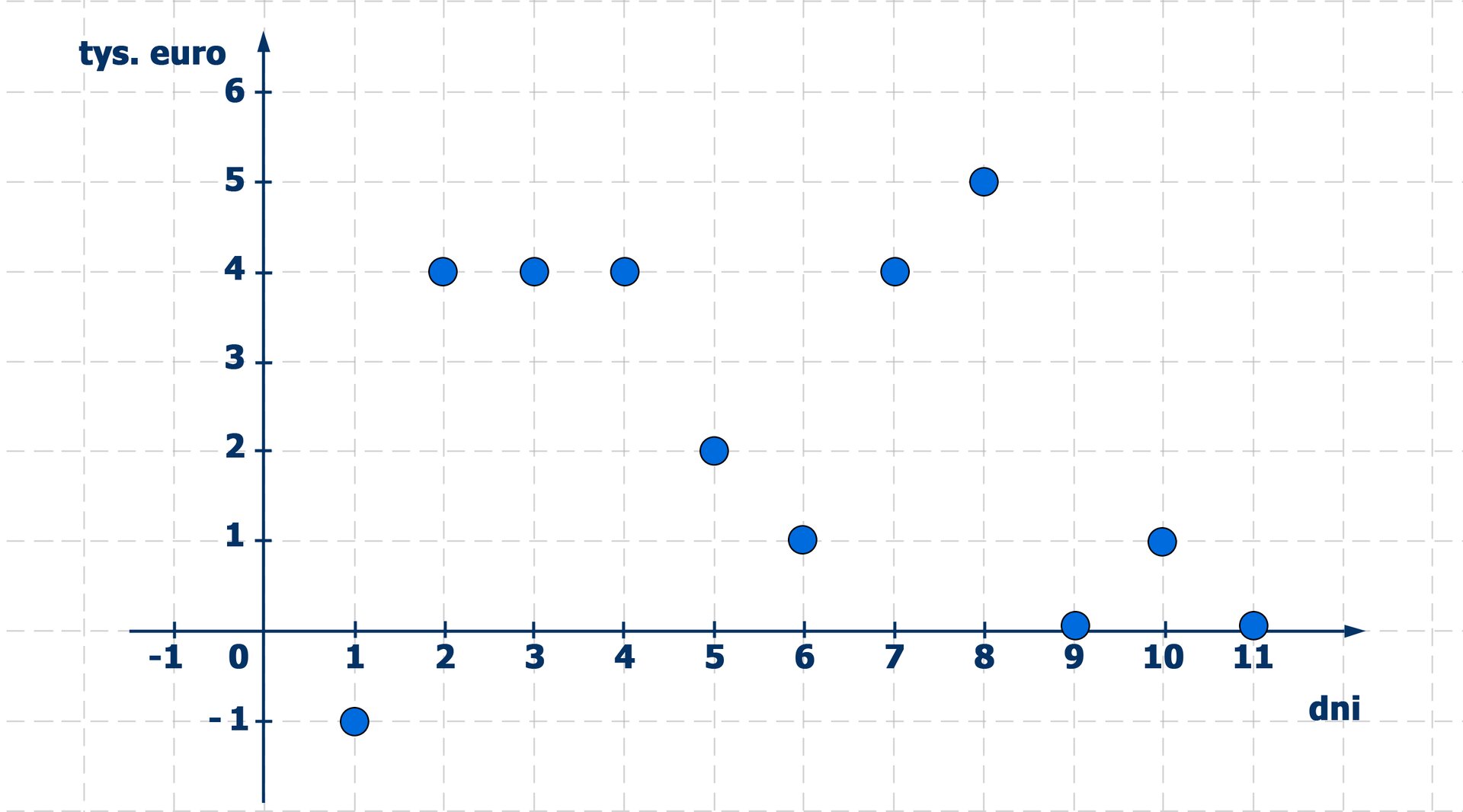
Klient zakupił lodówkę za kwotę tys. euro (czyli stan jego konta zmniejszył się o tys. euro w momencie dokonania płatności). Innych zakupów tego dnia już nie zrobił. Z wykresu odczytujemy, że zakup ten nastąpił dnia miesiąca, gdyż dnia stan konta wynosił tys. euro, a dnia tys. euro, a w żadnym innym dniu stan konta nie był o tys. euro niższy, niż w dniu poprzednim.
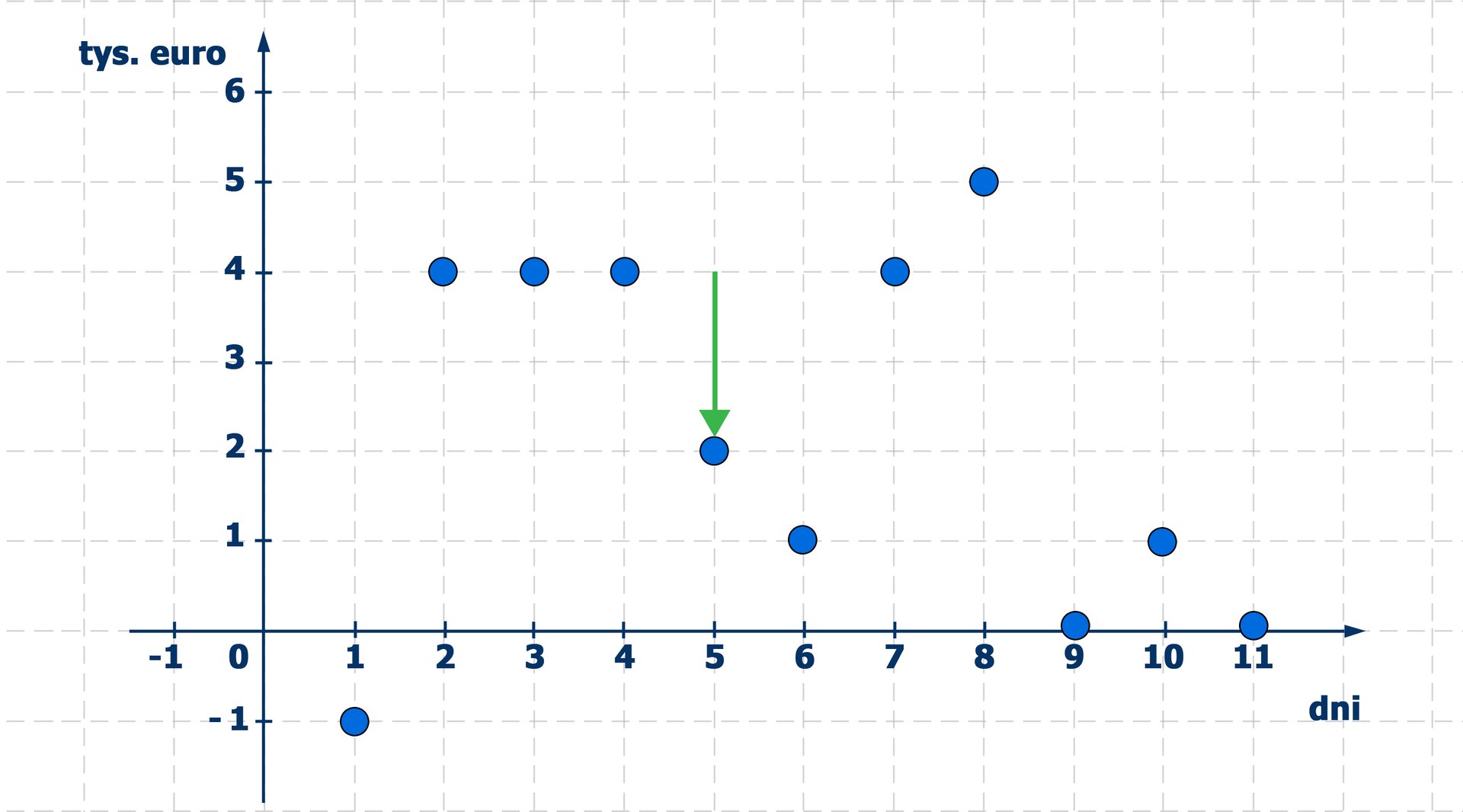
Konto klienta zostało zasilone kwotą tys. euro. Którego dnia miesiąca zostało zasilone konto taką kwotą? Z wykresu możemy odczytać, że nastąpiło to w dniu miesiąca.
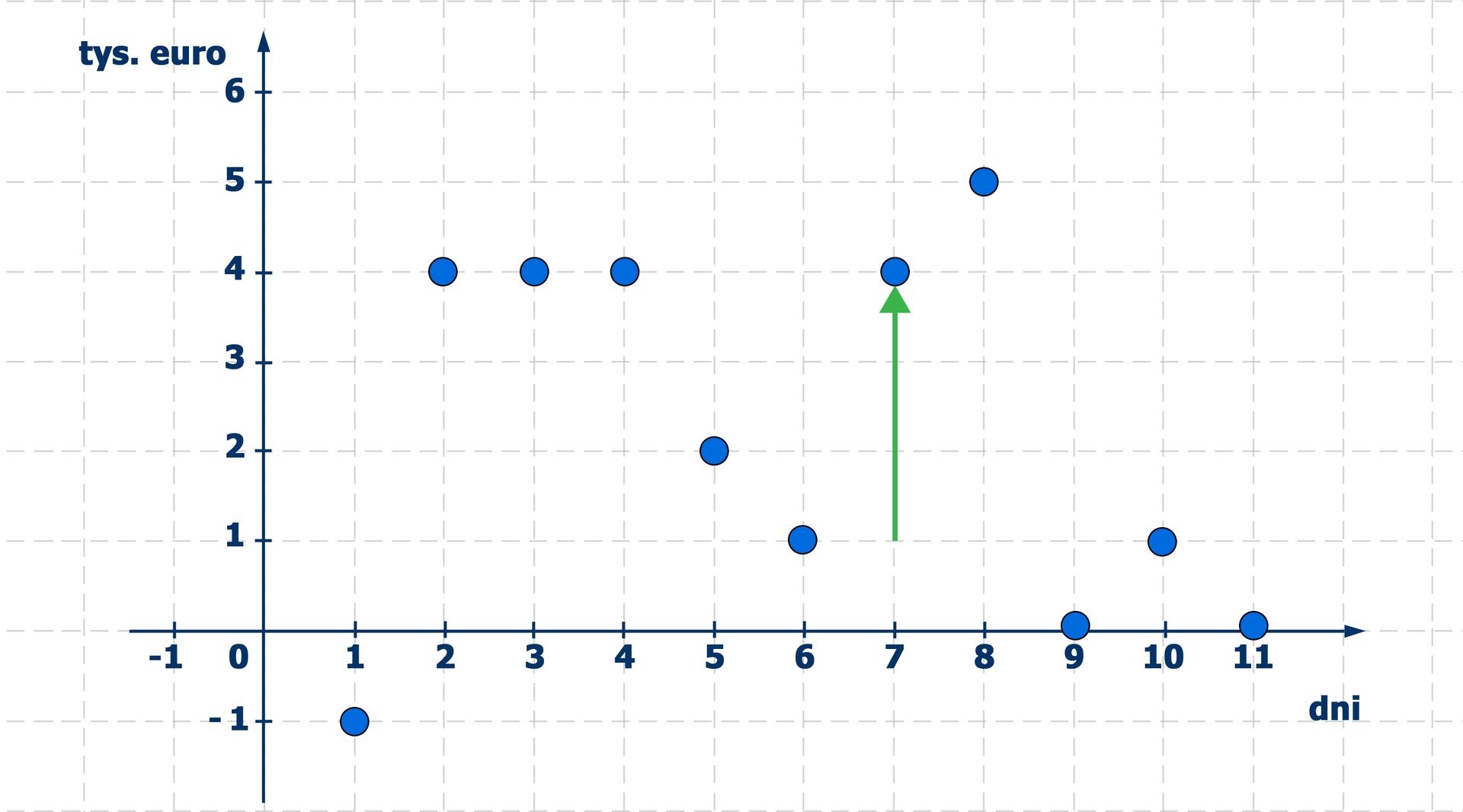
Kiedy stan konta klienta był równy zero? Z wykresu odczytujemy, że klient miał zerowy stan konta i dnia miesiąca. W przypadku niektórych kont banki dopuszczają sytuację, w której klient wypłaca z konta więcej pieniędzy niż posiada na koncie. Powstaje wówczas tzw. debet. Możemy, analizując ciągle ten sam wykres, zapytać, czy na koncie klienta był w tym okresie debet, a jeśli był, to w jakiej wysokości. Debet ilustrują te punkty wykresu, które znajdują się poniżej osi poziomej układu współrzędnych, a więc punkty odpowiadające ujemnym wartościom funkcji. Z wykresu odczytujemy, że tylko w dniu miesiąca miała miejsce taka sytuacja. Wielkość debetu wyniosła .
Powyższe przykłady pokazują, że w praktyce niekiedy istotne jest określenie, w jakim przypadku funkcja przyjmuje wartość . Są też sytuacje, gdy wygodniej jest porównywać wartości funkcji z inną szczególną wartością tej funkcji. Na przykład, gdy analizujemy wykres temperatury ciała człowieka w pewnym przedziale czasowym, to temperaturę porównujemy z wartością C. Jest to tzw. normalna temperatura ciała człowieka. Temperatura ciała wyższa od tej wartości, ale nie większa niż wskazuje na stan podgorączkowy. Temperatura ciała wyższa niż C oznacza gorączkę. Temperatura ciała człowieka niższa niż C oznacza osłabienie organizmu.
Na rysunku przedstawiony jest wykres temperatury ciała pacjenta, mierzonej co godzinę, przez kolejnych godzin.
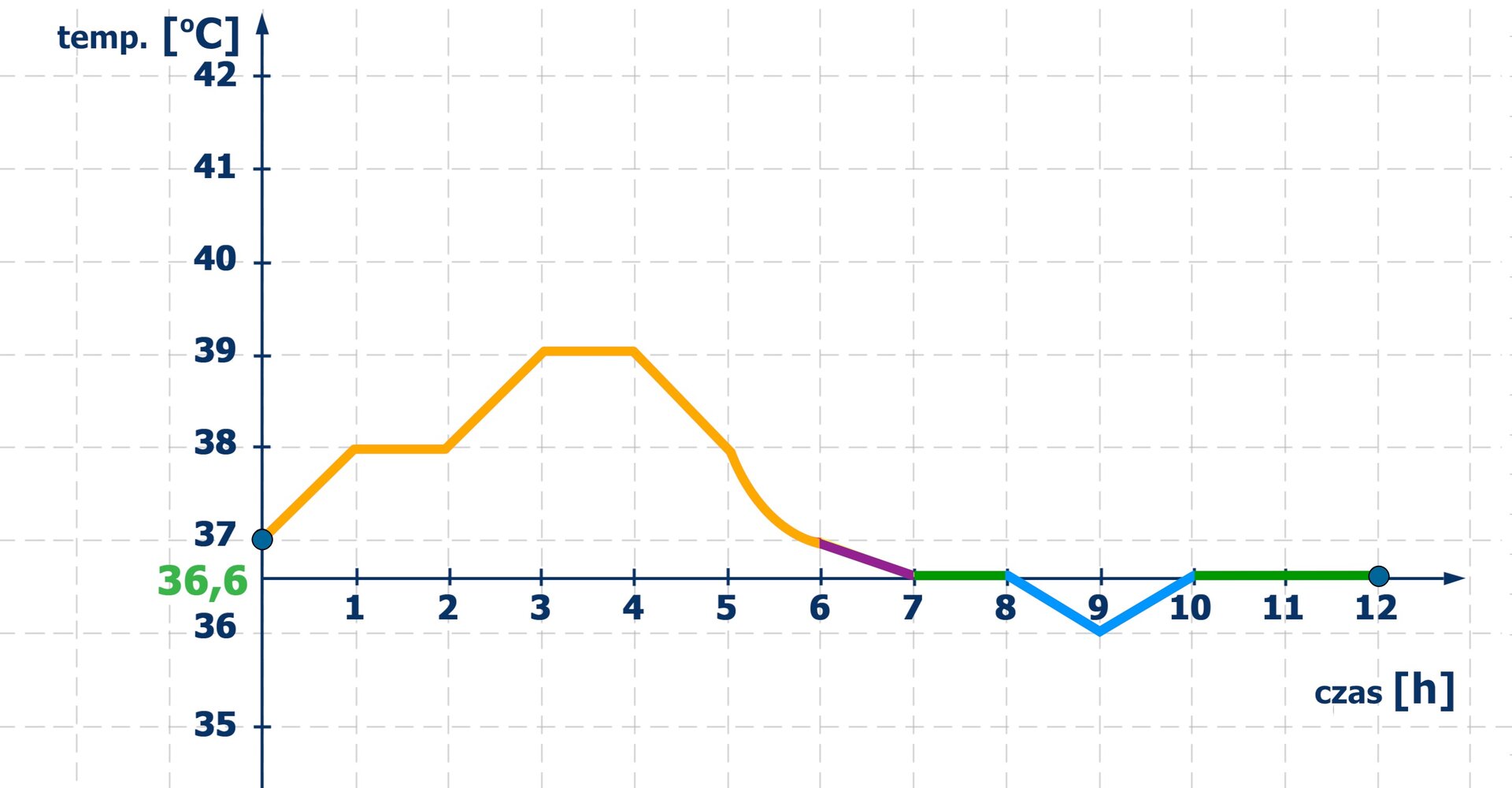
Określmy kilka przykładowych wartości temperatury ciała tego pacjenta. W początkowym momencie mierzenia, czyli w chwili pacjent miał stan podgorączkowy, temperatura jego ciała była równa C. W chwili temperatura jego ciała wynosiła C, a więc miał wówczas gorączkę. Po siedmiu godzinach pomiaru temperatura ciała pacjenta przyjęła wartość normalną i taka temperatura utrzymywała się przez godzinę, do chwili . Przez następne dwie godziny pacjent był osłabiony, ale od chwili aż do końca pomiaru, czyli do chwili znowu powróciła u niego temperatura normalna. Możemy więc powiedzieć, że normalna temperatura odnotowana była w dwóch przedziałach czasowych oraz .
W praktyce często występują charakterystyczne wartości różnych wielkości, często inne niż zero, w stosunku do których odnosimy mierzone wartości. Np. temperatura C, a więc temperatura wrzenia wody w warunkach normalnego ciśnienia, – dopuszczalna prędkość poruszania się pojazdów po drogach na obszarach zabudowanych, metrów n.p.m. – tzw. „granica śmierci” w górach.
Gdy dziedziną lub zbiorem wartości funkcji jest zbiór nieograniczony, to jesteśmy w stanie narysować jedynie pewien fragment wykresu tej funkcji (ze względu na ograniczone rozmiary kartki papieru lub ekranu monitora). Jeśli narysowany jest jedynie fragment wykresu funkcji i nie wiemy nic więcej o tej funkcji, to nie możemy na podstawie tego fragmentu wykresu wyciągać wniosków, które dotyczą tych części wykresu, których rysunek nie przedstawia. Na przykład na podstawie przedstawionego fragmentu wykresu funkcji możemy podać jej miejsce zerowe i stwierdzić, że w widocznym na rysunku przedziale innych miejsc zerowych ta funkcja nie ma.

Jeśli wiedzielibyśmy, że funkcja przedstawiona na wykresie jest dla każdego rzeczywistego określona wzorem
to wyznaczenie jej wszystkich miejsc zerowych sprowadziłoby się do rozwiązania równania , co równoważnie zapisujemy , skąd , czyli .