Jeżeli dwie osoby podnoszą ciało o ciężarze 100 N, to mówimy, że są jednakowo silne. Jeżeli podniosą je na wysokość jednego metra, to wykonają taką samą pracę. A jeżeli jedna z nich podniesie ten ciężar w czasie 1 sekundy, a druga w czasie 2 sekund, to czym się różnią prace wykonane przez te osoby? Która osoba jest silniejsza i czy oznacza to, że jest ona mocniejsza?

ReFbl1JU6o7YI1

Zdjęcie przedstawia z bliska ścianę wyłożoną białymi kafelkami stojącą pod kątem około sześćdziesięciu stopni do obserwatora zdjęcia. Zaczyna się za prawą krawędzią kadru, a kończy mniej więcej w 1/4 odległości od lewej krawędzi. W ścianie jest są dwie dziury, jedna gotowa po prawej stronie centralnego kafelka, a druga właśnie wiercona. Przednia część wiertarki trzymanej w rękach zajmuje lewą stronę kadru. Obracające się szybko wiertło wierci dziurę w ścianie. — Gdy kupujesz elektronarzędzia lub sprzęt AGD, często bierzsz pod uwagę ich moc. Czy wiesz jednak, co tak naprawdę oznacza ten termin?

Już potrafisz

stwierdzić, że pracę wykonuje siła równoległa do przemieszczenia;
podać definicję pracy i obliczyć jej wartość jako iloczyn siły i przesunięcia;
podać definicję jednostki pracy w układzie SI;
wyrażać czas w sekundach, które są jednostką w układzie SI.

Nauczysz się

podawać definicję mocy i jej jednostki;
przeliczać jednostki mocy;
obliczać moc urządzenia wykonującego pracę.

iabC2aUxVg_d5e156

moc

– wielkość fizyczna wyrażona liczbowo jako iloraz pracy i czasu jej wykonania:

moc = \frac{praca}{czas wykonania tej pracy}

lub

P = \frac{W}{t}

Moc informuje nas, ile pracy może wykonać dane urządzenie lub osoba w określonej jednostce czasu, np. w ciągu sekundy. Jeżeli w poszczególnych sekundach wykonana praca jest różna, to z powyższej zależności obliczymy średnią moc.

Co to znaczy, że jakieś urządzenie ma większą moc? Oznacza to, że taką samą pracę może wykonać w krótszym czasie, czyli szybciej niż urządzenie o mniejszej mocy, lub też w tym samym czasie wykona większą pracę.

wat

– jednostka mocy (W); urządzenie ma moc 1 wata [W] jeśli w ciągu 1 sekundy [s] wykona pracę 1 dżula [J], czyli:

1 W = \frac{1 J}{1 s}

Nazwa tej jednostki pochodzi od nazwiska szkockiego inżyniera i konstruktora Jamesa WattaJames WattJamesa Watta.
W przypadku występowania dużych mocy używamy jednostki tysiąc razy większej, czyli kilowatów (np. moc silnika tramwajowego wynosi 200 kW) lub megawatów (np. elektrownia ma moc 1200 MW), a małe moce wyrażamy w miliwatach (moc lecącej muchy ma wartość 0,3 mW).

Ciekawostka

W motoryzacji jako jednostki mocy tradycyjnie używa się jeszcze koni mechanicznych [KM]. Zbliżoną co do wartości do konia mechanicznego jednostkę mocy zdefiniował James Watt. Jest to tzw. koń parowy [HP]. Zależność pomiędzy tymi jednostkami jest następująca:

1 KM = 735,49875 W = 0,9863 HP

Moc $1 KM$ odpowiadała mocy zaprzęgu z jednym koniem, $2 KM$ – z dwoma końmi itd. Jest to tzw. moc brutto konia, liczona z pominięciem rozmaitych strat. Do zapisu wartości mocy używa się też często skrótu niemieckiego – PS.

R1TDcCh5MeELE1

Koń mechaniczny — Fizyka inspiruje również artystów

Ćwiczenie 1

RpUQnuDy7GEwi1

Połącz w pary te liczby mianowane, które wyrażają tę samą moc.

0,03 W, 0,0003 W, 3000000 W, 300000 W

0,3 mW
3 MW
30 mW
300 kW

Źródło: Helena Nazarenko-Fogt <Helena.Nazarenko-Fogt@up.wroc.pl>, licencja: CC BY 3.0.

Kto jest mocniejszy?

Doświadczenie 1

Problem badawczy

Czy to, jak szybko człowiek wykonuje pracę, zależy jego masy?
Czy szybkość wykonywania pracy (moc), przypadająca na 1 kg masy ciała człowieka jest zawsze taka sama?

Hipoteza

Człowiek o większej masie szybciej wykona taką samą pracę (ma większą moc).
Moc przypadająca na 1 kg masy ciała człowieka jest w przybliżeniu taka sama.

Co będzie potrzebne

linijka;
stoper;
waga łazienkowa.

Instrukcja

Wybierz mało uczęszczaną klatkę schodową o różnicy wysokości dwóch pięter.
Policz liczbę schodów między dwoma piętrami N.
Linijką zmierz wysokość jednego stopnia schodów h. Najlepiej zmierz wysokość kilku różnych stopni $h_{1}, h_{2} i h_{3}$ i oblicz średnią wysokość pojedynczego stopnia $h_{śr}$ . Wysokość tę wyraź w metrach. Pamiętaj o zaokrągleniu wyników obliczeń do dwóch miejsc po przecinku (dokładność pomiaru nie powinna przekraczać jednego centymetra).
Wyznacz swoją masę m i wyraź ją w kilogramach [kg].
Stoperem zmierz czas, w którym wbiegasz na drugie piętro t. Wyraź go w sekundach [s] z dokładnością do jednego miejsca po przecinku.
Po odpoczynku możesz powtórzyć pomiar czasu, a do dalszych obliczeń wziąć jego wartość średnią. Pamiętaj o zaokrągleniu wyników obliczeń do jednego miejsca po przecinku.
Oblicz pokonaną wysokość H, mnożąc liczbę schodów N i wysokość pojedynczego stopnia: $H = N \cdot h$ . Wynik podaj w metrach [m] z dokładnością do jednego miejsca po przecinku.
RkXMlN8ewkW4x1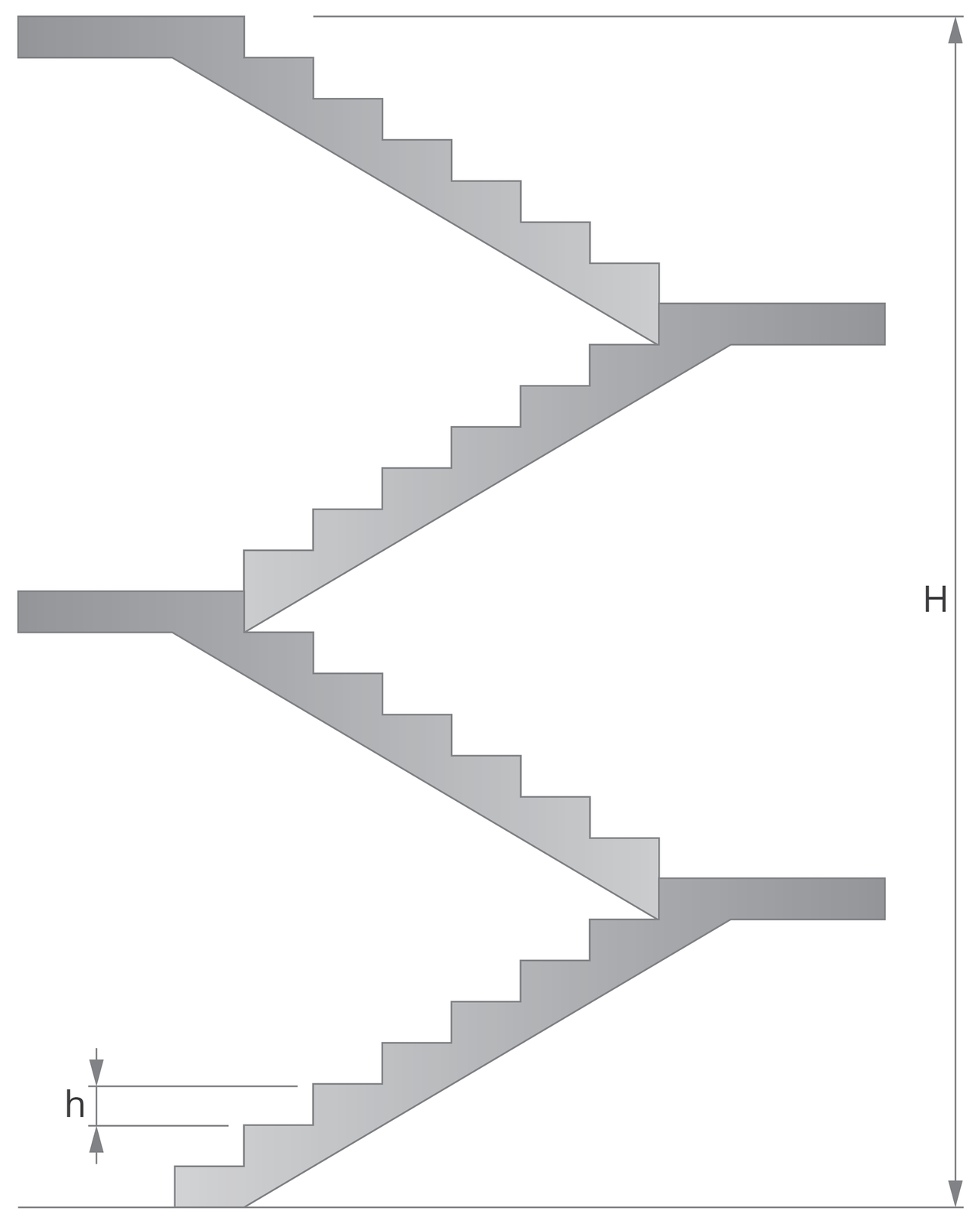
Jak zmierzyć wysokość schodów?
Oblicz pracę wykonaną podczas biegu: $W = m \cdot g \cdot H$ . Wynik podaj w dżulach z dokładnością do jednego dżula [J].
Oblicz moc, z jaką pracowałaś/eś podczas biegu: $P = \frac{W}{t}$ . Wynik podaj w watach z dokładnością do jednego wata [W].
Oblicz moc przypadającą na 1 kilogram twojej masy: $\frac{P}{m}$ . Wynik podaj w watach na kilogram [kg] z dokładnością do jedności.
Wyniki pomiarów i obliczeń wpisz do tabeli pomiarów.
Tabela pomiarów
$N$
$h [m]$
$h_{ś r} [m]$
$m [kg]$
$t [s]$
$H = N \cdot h_{ś r} [m]$
$W = m \cdot g \cdot H [J]$
$P = \frac{W}{t} [W]$
$\frac{P}{m} [\frac{W}{kg}]$
$h_{1} =$
$h_{2} =$
$h_{3} =$

Podsumowanie

Zbierz informacje o wynikach pomiarów uzyskanych przez inne osoby z klasy i przedstaw je w formie tabeli. Wpisuj wyniki, zaczynając od osoby o najmniejszej, a kończąc na osobie o największej masie.
Zebrane wyniki pomiarów wszystkich uczestników doświadczenia
$L . p .$
$m [kg]$
$P = \frac{W}{t} [W]$
$\frac{P}{m} [\frac{W}{kg}]$
1
2
3
4
5
6
7
8
9
10
Przeanalizuj liczby w tabeli i zapisz wnioski:
1. Jeśli wraz ze wzrostem masy ciała (druga kolumna tabeli) rośnie moc (trzecia kolumna tabeli), zapisz, że pierwsza z hipotez jest prawdziwa. Wniosek będzie więc brzmiał: Człowiek o większej masie ma większą moc. Jeśli wyniki w tabeli tego nie potwierdzają – napisz, że pierwsza z hipotez nie została potwierdzona.
2. Jeśli liczby zawarte w ostatniej kolumnie są w przybliżeniu takie same, zapisz, że druga z hipotez jest prawdziwa. Wniosek będzie więc brzmiał: Moc przypadająca na 1 kg masy ciała człowieka jest w przybliżeniu taka sama. Jeśli liczby w ostatniej kolumnie znacznie się różnią, zapisz, że druga z hipotez nie została potwierdzona. Pamiętaj, że wyniki pomiarów obarczone są niepewnością pomiarową i do potwierdzenia hipotezy liczby w ostatniej kolumnie nie muszą być idealnie takie same.
Jeśli zebrane przez ciebie dane nie potwierdzają żadnej z postawionych hipotez, zastanów się, co może być tego przyczyną. Może należy rozdzielić pomiary chłopców od pomiarów dziewczynek? Może nie wszyscy uczniowie w klasie mają tyle samo lat? A może są wśród was utalentowani, wytrenowani sportowcy i to ich wyniki znacząco odbiegają od wyników przeciętnego nastolatka? Zapisz w dwóch, trzech zdaniach swoje przemyślenia.

Przejdźmy teraz do obliczeń. Oto przykłady.

Przykład 1

Z jaką mocą pracuje człowiek, który w ciągu pół godziny wykonuje pracę $360 kJ$ ?
Analiza zadania:
Moc, z jaką pracuje człowiek, obliczamy według wzoru: $P = \frac{W}{t}$ .
Wymagane wielkości:
$W$ – wykonywana praca;
$t$ – czas wykonania pracy.
Dane:
$W = 360 kJ = 360 000 J$ ,
$t = 0,5 h = 1 800 s$ .
Szukane:
$P = ?$
Zwróć uwagę, że przed przystąpieniem do obliczeń należało zamienić jednostki czasu z godzin na sekundy. Teraz przystąpmy do obliczeń.
Obliczenia:
$P = \frac{W}{t} = \frac{360 000 J}{1 800 s} = 200 W$ .
Odpowiedź:
Człowiek pracował z mocą $200 W$ .

Przykład 2

Oblicz pracę, jaką wykona silnik odkurzacza o mocy $1,2 kW$ w ciągu 20 minut.
Analiza zadania:
Moc silnika odkurzacza obliczymy ze wzoru: $P = \frac{W}{t}$ .
Wzór ten po przekształceniu pozwoli nam obliczyć pracę.
$P = \frac{W}{t} / \cdot t$
$P \cdot t = \frac{W}{t} \cdot t$
$P \cdot t = \frac{W}{t} \cdot t$
$W = P \cdot t$
Pracę silnika odkurzacza obliczymy więc ze wzoru: $W = P \cdot t .$
Wymagane wielkości:
$P$ – moc odkurzacza,
$t$ – czas pracy odkurzacza.
Dane:
$P = 1,2 kW = 1 200 W$ ,
$t = 20 \min = 1200 s$ .
Szukane:
$W = ?$
Możemy zatem przystąpić do obliczeń.
Obliczenia:
$W = P \cdot t = 1 200 W \cdot 1 200 s = 1 440 000 J = 1,4 MJ$ .
Odpowiedź:
Silnik wykonał pracę 1 miliona 440 tysięcy dżuli, czyli 1,4 megadżuli.

Polecenie 1

Obejrzyj film i wzorując się na rozumowaniu Młodego Fizyka, odpowiedz na pytanie: czy silniejszy zawsze oznacza to samo co mocniejszy?

R1KKInTnYDdVW1

Czy silniejszy znaczy to samo co mocniejszy?

Przykład 3

Aby jechać po poziomym torze ze stałą szybkością $5 \frac{m}{s}$ , rowerzysta musi pokonywać opory ruchu o wartości $50 N$ . Z jaką mocą musi pracować rowerzysta?
Analiza zadania:
Moc rowerzysty: $P = \frac{W}{t}$ .
Droga przebyta przez rowerzystę: $s = v \cdot t$ .
Praca rowerzysty: $W = F \cdot s = F \cdot v \cdot t$ .
Wymagane wielkości:
$F$ – siła,
$v$ – prędkość.
Dane:
$F = 50 N$ ,
$v = 5 \frac{m}{s}$ .
Szukane:
$P = ?$
Obliczenia:
Moc można obliczyć, korzystając ze wzoru:
$P = \frac{W}{t}$ .
Wzór na pracę można podstawić do wzoru na moc. Otrzymujemy wówczas zależność:
$P = \frac{F \cdot s}{t} = F \cdot \frac{s}{t}$ .
Zwróć uwagę, że wyrażenie $\frac{s}{t}$ oznacza wartość prędkości, zatem otrzymujemy zależność:
$P = F \cdot v$ .
A zatem:
$P = F \cdot v = 50 N \cdot 5 \frac{m}{s} = 250 W$ .
Odpowiedź:
Rowerzysta pracował z mocą 250 watów.

iabC2aUxVg_d5e512

Podsumowanie

Moc to szybkość wykonywania pracy, czyli jest równa liczbowo pracy wykonanej w jednostce czasu. Moc $P$ jest równa ilorazowi pracy $W$ i czasu $t$ , w którym ta praca została wykonana:
$P = \frac{W}{t}$
Jednostką mocy w układzie SI jest wat. Urządzenie ma moc jednego wata, jeśli w ciągu sekundy wykonuje pracę jednego dżula:
$1 W = \frac{1 J}{1 s}$

Praca domowa

Polecenie 2.1

Aby rozładować towar z samochodu dostawczego, trzeba wykonać pracę $900 MJ$ . Oblicz czas, w jakim pracę tę wykona maszyna o mocy $P_{1} = 300 kW$ , a w jakim maszyna o mocy $P_{2} = 450 000 W$ ? Wyniki podaj w sekundach oraz w minutach.

iabC2aUxVg_d5e566

Zadanie podsumowujące lekcję

Ćwiczenie 2

RnO8H4sueZVQq1

Uzupełnij tekst.

Traktor ma większą moc niż koń, dlatego w tym samym czasie wykona .................. pracę niż koń. Lokomotywa spalinowa ma mniejszą moc niż elektryczna, dlatego tę samą pracę wykona w .................... czasie. Silnik o większej mocy rozpędzi samochód do tej samej prędkości w .................. czasie.

Źródło: Helena Nazarenko-Fogt <Helena.Nazarenko-Fogt@up.wroc.pl>, licencja: CC BY 3.0.

iabC2aUxVg_d5e600

Biogram

James Watt

R1QtGaOkYJMnb1

[testowy tekst alternatywny] — James Watt – szkocki konstruktor i wynalazca

James Watt

19.01.1736–25.08.1819

James Watt urodził się w rodzinie cieśli i już w szkole ujawniły się jego wielkie zdolności matematyczne oraz techniczne. Pracował jako wytwórca i konstruktor przyrządów precyzyjnych najpierw w Londynie, a następnie na Uniwersytecie w Glasgow. Zasłynął jako twórca znaczących ulepszeń maszyny parowej: wydzieił komorę kondensacji pary, opracował zespół przekładni umożliwiających zastosowanie silnika parowego w pojazdach, zbudował regulator prędkości obrotowej silnika parowego (zwany regulatorem Watta).

Praca jako wielkość fizyczna

Maszyny proste. Wyznaczanie masy ciała przy użyciu dźwigni dwustronnej

Moc jako szybkość wykonywania pracy

Podsumowanie

Zadanie podsumowujące lekcję

Biogram

James Watt

$N$	$h [m]$	$h_{ś r} [m]$	$m [kg]$	$t [s]$	$H = N \cdot h_{ś r} [m]$	$W = m \cdot g \cdot H [J]$	$P = \frac{W}{t} [W]$	$\frac{P}{m} [\frac{W}{kg}]$
	$h_{1} =$
	$h_{2} =$
	$h_{3} =$

$L . p .$	$m [kg]$	$P = \frac{W}{t} [W]$	$\frac{P}{m} [\frac{W}{kg}]$
1
2
3
4
5
6
7
8
9
10