Objętość stożka
W tym materiale zawarte są informacje na temat objętości stożka. Poznasz wzór na objętość stożka oraz zależność między objętością stożka a objętością walca o takiej samej podstawie i takiej samej wysokości.
Wzór na objętość stożka
Film dostępny pod adresem /preview/resource/R1HIzrERCHAbm
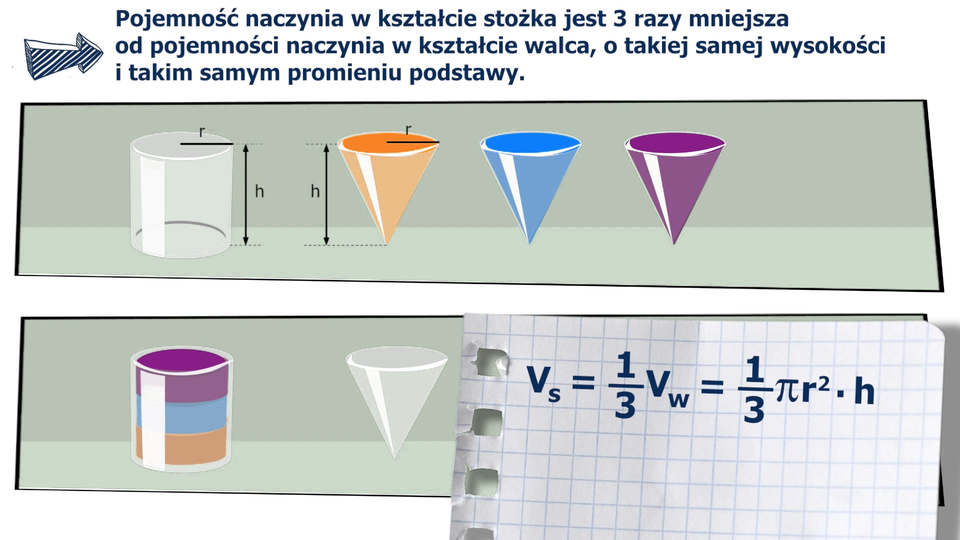
Animacja przedstawia wzór na objętość stożka wraz z jego uzasadnieniem.
Walec i stożek mają taki sam promień podstawy i taką samą wysokość.
Zaobserwuj, jak zmienia się stosunek objętości walca do objętości stożka wraz ze zmianą wysokości brył.
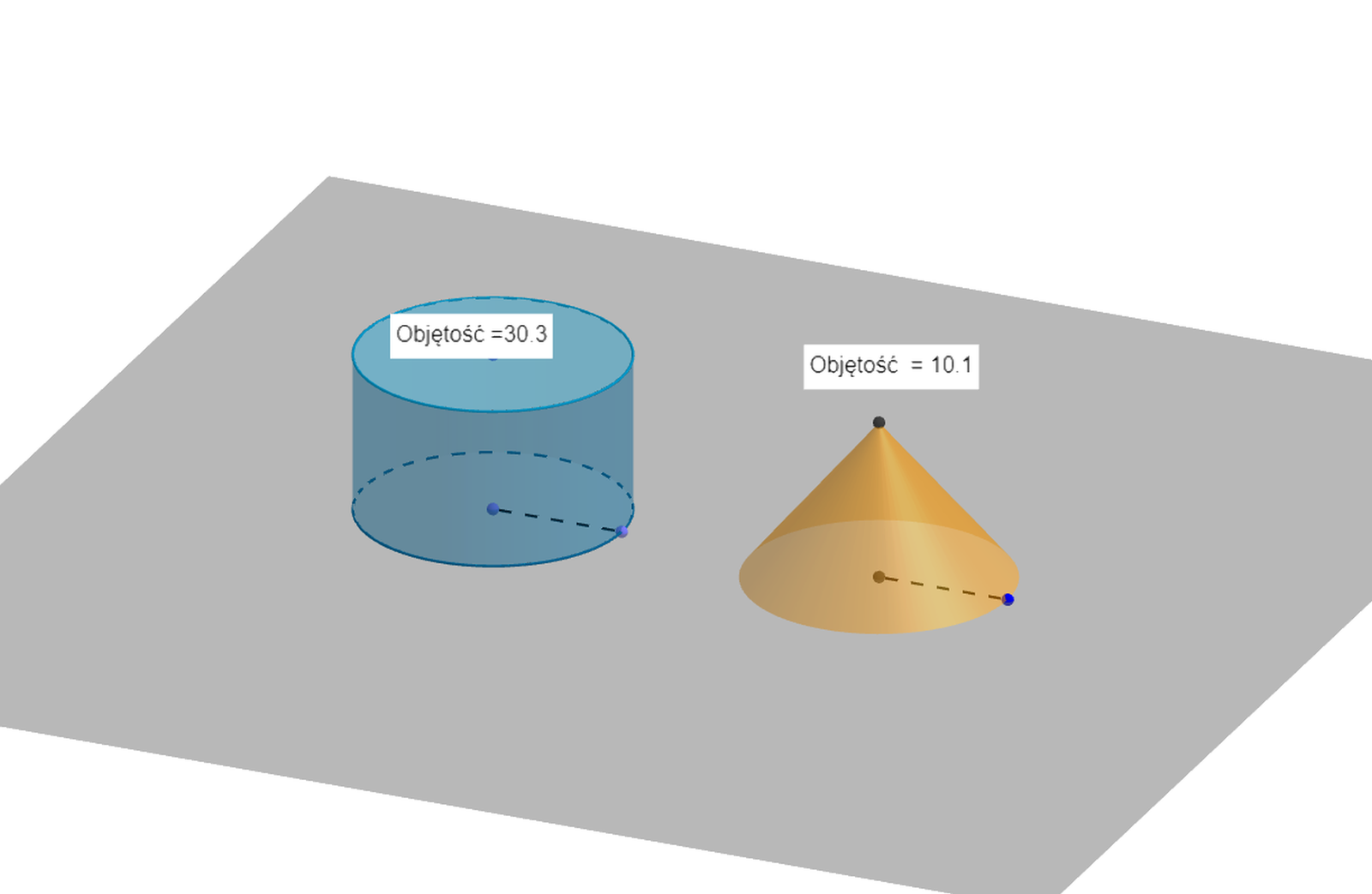
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PvrUTRXoq
Walec i stożek mają taki sam promień podstawy i taką samą wysokość . Zaobserwuj, jak zmienia się stosunek objętości walca do objętości stożka wraz ze zmianą wysokości brył.
Przyjmijmy, że promień podstawy stożka i walca jest równy . Obliczymy objętości podanych brył dla pięciu różnych wysokości i zastanowimy się, czy zachodzi jakaś analogia między ilorazem objętości walca do objętości stożka.
Niech . Zatem , oraz
.
Niech . Zatem , oraz
.
Niech . Zatem , oraz
.
Niech . Zatem , oraz
.
Niech . Zatem , oraz
.
Łatwo więc zauważyć, że stosunek objętości walca do objętości stożka zawsze jest równy .
Objętość stożka o wysokości i promieniu podstawy wyraża się wzorem:

Oblicz objętość stożka, którego wysokość jest równa , a promień podstawy .
Do wzoru na objętość stożka
podstawiamy:
Objętość stożka jest równa .
Ile porcji lodów można otrzymać z masy lodowej?

Obliczymy objętość masy lodowej potrzebnej do wykonania jednej porcji lodów, czyli objętość dwóch stożków o wspólnej podstawie. Wysokość jednego z tych stożków jest równa , a drugiego . Promień podstawy każdego ze stożków jest równy .
Na wykonanie jednej porcji lodów potrzeba około masy lodowej.
Obliczamy teraz, ile lodów można otrzymać z masy lodowej.
Ponieważ , a , zatem .
Z masy lodowej można wykonać lodów.
Obliczanie objętości stożka
Świeca wykonana z wosku o gęstości ma masę . Świeca ma kształt stożka o średnicy podstawy równej . W czasie godziny wysokość palącej się świecy zmniejsza się przeciętnie o . Świecę zapalono o godzinie . O której godzinie zgaśnie ta świeca?
Przyjmij .
Gęstość wosku podana jest w . Średnicę świecy zapiszemy więc w centymetrach, a jej masę w gramach, aby ujednolicić jednostki.

Oznaczmy:
– wysokość świecy.
Objętość stożka, w kształcie którego jest świeca, jest równa
Stąd
Zapisujemy równość wynikającą z tego, że masa substancji to iloczyn zajmowanej przez nią objętości przez gęstość tej substancji.
Z zapisanej równości wyznaczamy wysokość świecy.
W czasie godziny wysokość świecy zmniejsza się o , czyli świeca będzie paliła się godzin.
Świecę zapalono o godzinie , do północy paliła się więc godziny i godzin po północy.
Świeca zgaśnie o godzinie następnego dnia.
Przekrojem osiowym stożka jest trójkąt, którego tworząca jest równa . Pole powierzchni bocznej stożka jest równe . Oblicz objętość stożka.
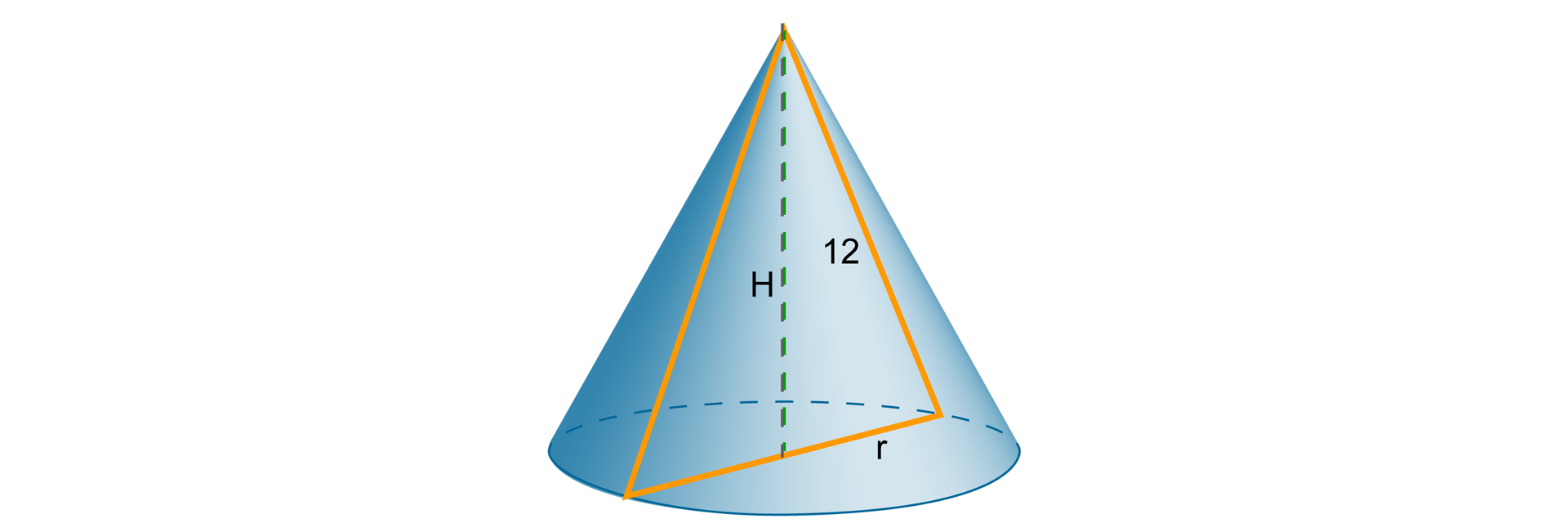
Aby obliczyć objętość stożka, należy najpierw znaleźć wysokość stożka i promień jego podstawy.
Promień podstawy stożka znajdujemy, korzystając z tego, że pole powierzchni bocznej stożka jest równe .
Zauważmy, że wysokość stożka jest zarazem wysokością jego przekroju osiowego.
Zatem trójkąt, którego boki mają długości , , (jak na rysunku), jest prostokątny.
Zapisujemy dla tego trójkąta równość wynikającą z twierdzenia Pitagorasa i wyznaczamy wysokość stożka.
Obliczamy objętość stożka.
Objętość stożka jest równa .
Element ma kształt walca, na którym umieszczony jest stożek.
Przekrojem osiowym tego walca jest kwadrat o polu . Objętość całej bryły wynosi .
Oblicz, ile puszek farby należy zakupić, aby pomalować cały element, jeżeli zawartość jednej puszki wystarcza na pomalowanie powierzchni. Przyjmij .
Oznaczmy:
– promień podstawy walca,
– wysokość walca,
– wysokość stożka,
– długość tworzącej stożka.
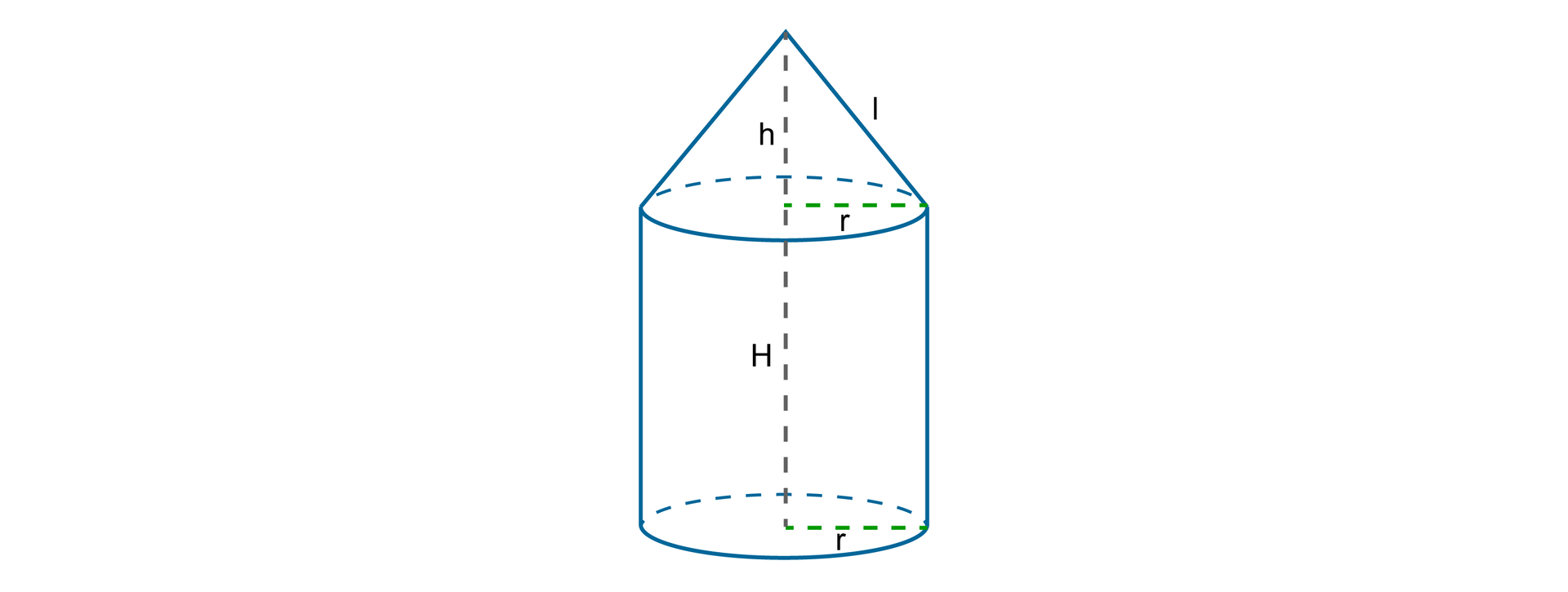
Przekrojem osiowym walca jest kwadrat o polu . Wynika z tego, że długość boku tego kwadratu jest równa , czyli . Wysokość walca jest więc równa , a promień jego podstawy . Objętość elementu jest równa sumie objętości walca i stożka.
Dla ułatwienia obliczeń wyłączamy z obu składników wspólne czynniki poza nawias.
Teraz, korzystając z twierdzenia Pitagorasa, obliczamy długość tworzącej stożka.
Obliczamy pole powierzchni całkowitej elementu, czyli sumę pola koła (podstawy bryły), pola powierzchni bocznej walca i pola powierzchni bocznej stożka.
Jedna puszka farby wystarcza na pomalowanie powierzchni. Ponieważ , zatem należy kupić puszek farby.
Oblicz objętość stożka otrzymanego w wyniku obrotu trójkąta prostokątnego wokół prostej . Przyjmij .
Na rysunku poniżej przedstawiono przekrój osiowy trzech stożków.
b) 1. , 2. , 3. , 4. , 5. , 6.
c) 1. , 2. , 3. , 4. , 5. , 6.
Karnisz składa się z trzech elementów. Dwa elementy są jednakowe i każdy z nich ma kształt stożka o średnicy podstawy i wysokości . Trzeci element ma kształt walca o wysokości i średnicy podstawy . Oblicz, ile aluminium zużyto na wykonanie karnisza. Przyjmij .

Odpowiedź: Zużyto 1. , 2. , 3. , 4. , 5. aluminium.
Powierzchnia boczna elementu składającego się ze stożka i walca (jak na rysunku) jest równa . Promień podstawy walca jest równy , a tworząca stożka . Oblicz objętość elementu.

Odpowiedź: Objętość tego elementu wynosi 1. , 2. , 3. , 4. , 5. .
Do szklanki w kształcie walca wstawiono lejek w kształcie stożka. Naczynia mają równe wysokości i średnice.
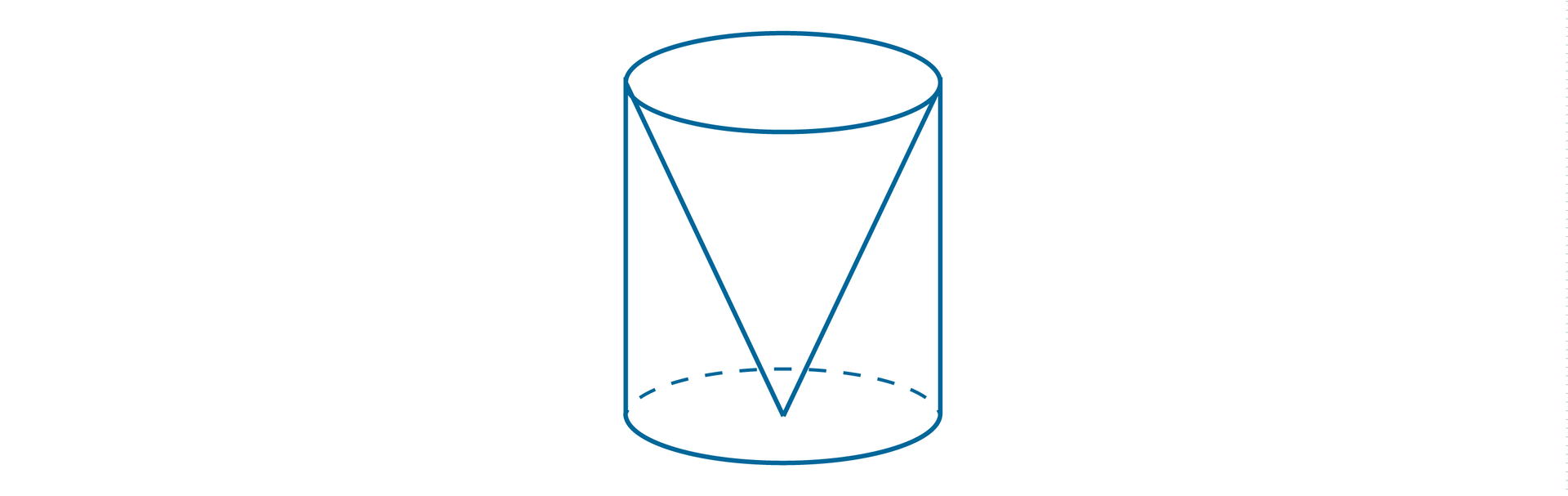
Odpowiedź: Objętość większej bryły wynosi 1. , 2. , 3. , 4. , 5. , 6. .
Oblicz pole powierzchni mniejszej z tak otrzymanych brył.
Odpowiedź: Pole powierzchni mniejszej bryły wynosi 1. , 2. , 3. , 4. , 5. , 6. .
Odpowiedź: Objętość stożków wynosi kolejno 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. oraz
1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. . Ich stosunek wynosi 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. , 9. .
Odpowiedź: Stosunek objętości stożków wynosi 1. , 2. , 3. , 4. .
Odpowiedź: Objętość stożka wynosi 1. , 2. , 3. , 4. .
Odpowiedź: Objętość stożka 1. dwukrotnie, 2. jednokrotnie, 3. zmniejszy, 4. trzykrotnie, 5. zwiększy, 6. czterokrotnie, 7. sześciokrotnie, 8. pięciokrotnie się 1. dwukrotnie, 2. jednokrotnie, 3. zmniejszy, 4. trzykrotnie, 5. zwiększy, 6. czterokrotnie, 7. sześciokrotnie, 8. pięciokrotnie.
Odpowiedź: Objętość tego stożka wynosi 1. , 2. , 3. , 4. , 5. .
Odpowiedź: Objętość tego stożka wynosi 1. , 2. , 3. , 4. , 5. .
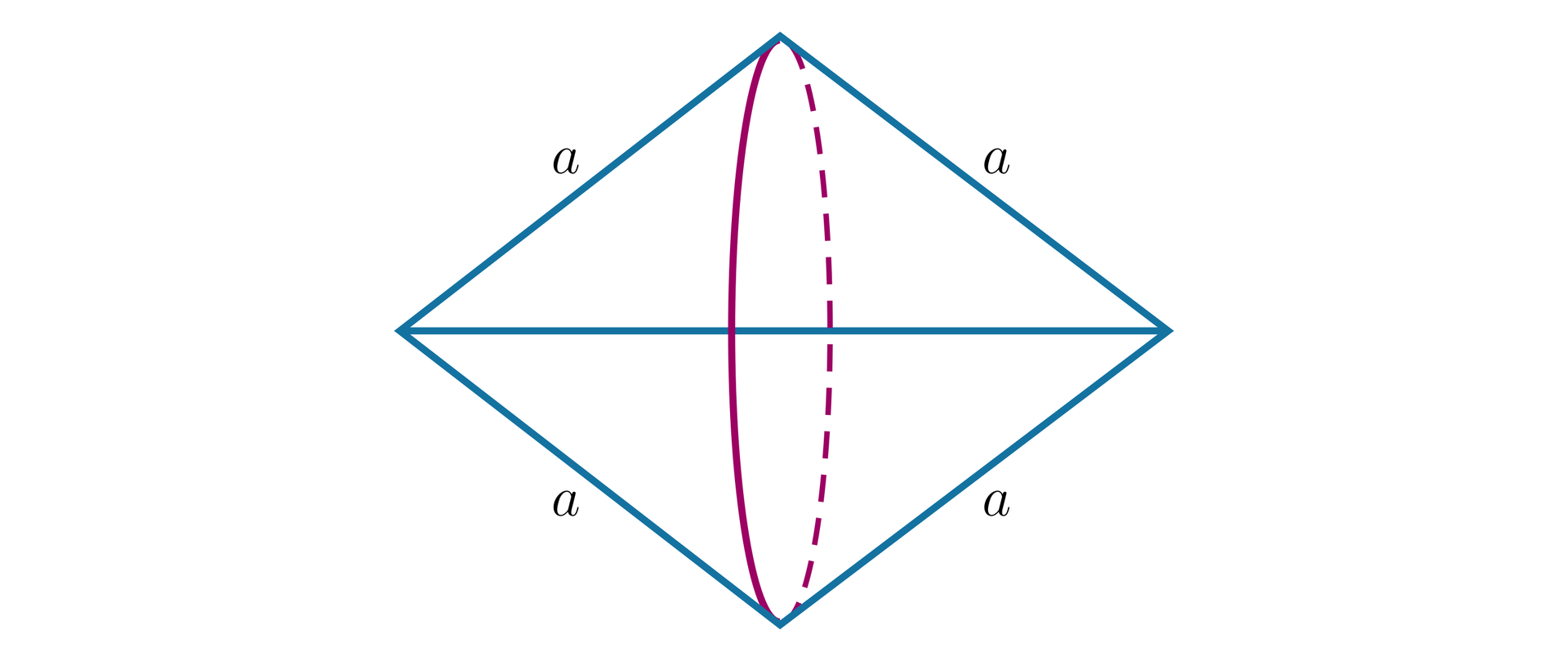
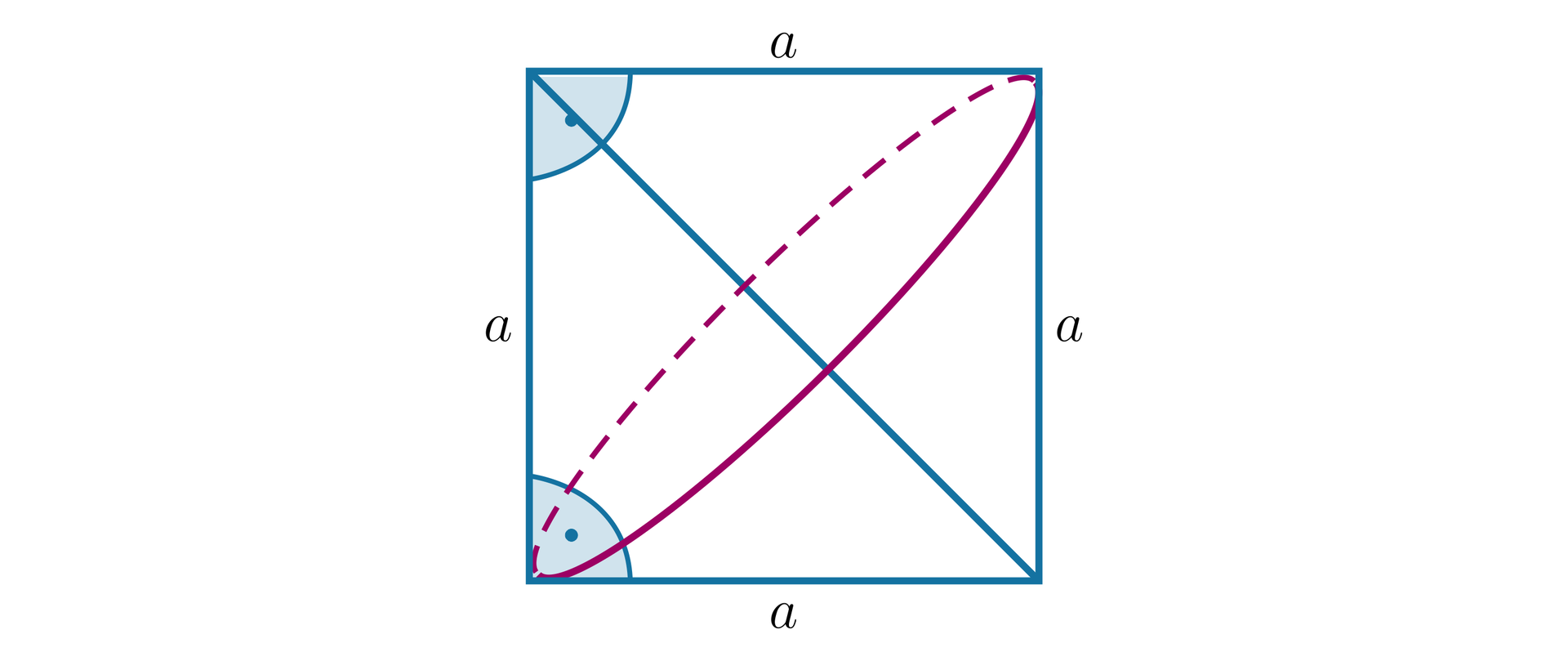
Naszkicuj bryłę powstałą w wyniku obrotu:
trójkąta równoramiennego wokół jego podstawy,
kwadratu wokół jego przekątnej.
Jaką wysokość będzie miał ten stożek? Zaznacz poprawną odpowiedź. Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Odpowiedź: Objętość stożka wynosi 1. , 2. , 3. , 4. .
Odpowiedź: Objętość stożka wynosi 1. , 2. , 3. , 4. .