Obliczanie długości boków w trójkącie prostokątnym
Korzystając z twierdzenia Pitagorasa, można obliczyć długość jednego z boków trójkąta prostokątnego, mając dane długości dwóch pozostałych boków.
W trójkącie prostokątnym długości przyprostokątnych są równe i . Znajdźmy długość przeciwprostokątnej tego trójkąta.

Zapisujemy równość wynikającą z twierdzenia Pitagorasa, z której wyznaczamy długość przeciwprostokątnej.
Równanie
ma dwa rozwiązania lub . Długość boku trójkąta wyraża się liczbą dodatnią, zatem uwzględniamy tylko rozwiązanie dodatnie
Przeciwprostokątna trójkąta ma długość .
Jedna z przyprostokątnych trójkąta prostokątnego ma długość , a przeciwprostokątna ma długość . Oblicz długość drugiej przyprostokątnej.

Oznaczamy – długość drugiej przyprostokątnej, . Korzystamy z twierdzenia Pitagorasa.
Druga z przyprostokątnych ma długość .
W trójkącie prostokątnym dwa boki mają długości i . Znajdź długość trzeciego boku tego trójkąta.
Oznaczmy – szukaną długość boku trójkąta .
Długość boku znajdziemy, korzystając z twierdzenia Pitagorasa.
Rozpatrzymy dwa przypadki:
przypadek | przypadek |
|---|---|
Bok, którego długości szukamy, jest przyprostokątną trójkąta. | Bok, którego długości szukamy jest przeciwprostokątną trójkąta. |
Długość trzeciego boku trójkąta jest równa lub .
W podanym twierdzeniu wskaż założenie i tezę. Czy twierdzenie jest prawdziwe?
Jeżeli liczba naturalna dodatnia jest wielokrotnością , to jest podzielna przez
.Jeżeli pole kwadratu jest równe , to jego obwód jest równy .
Jeżeli punkt leży w układzie współrzędnych na osi , to jego druga współrzędna jest równa .
Jeżeli wielokąt jest trapezem, to jego przekątne zawsze przecinają się pod kątem prostym.
Sformułuj podane twierdzenie, korzystając ze schematu „jeżeli … to”.
Pole kwadratu o boku długości jest równe .
W trójkącie równobocznym każdy kąt ma miarę .
Liczba naturalna podzielna przez cztery jest liczbą parzystą.
Pole kwadratu zbudowanego na przeciwprostokątnej wynosi , a pole kwadratu zbudowanego na krótszej przyprostokątnej wynosi . Wynika stąd, że obwód tego trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , pole 1. , 2. , 3. , 4. , 5. , 6. .Pola kwadratów zbudowanych na przyprostokątnych wynoszą kolejno oraz . Wynika stąd, że obwód tego trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , pole 1. , 2. , 3. , 4. , 5. , 6. .Pole kwadratu zbudowanego na przeciwprostokątnej wynosi , a pole kwadratu zbudowanego na krótszej przyprostokątnej wynosi . Wynika stąd, że obwód tego trójkąta wynosi 1. , 2. , 3. , 4. , 5. , 6. , pole 1. , 2. , 3. , 4. , 5. , 6. .
Wszystkie znajdujące się na rysunku trójkąty są prostokątne. Trójkąty niebieskie są przystające.
Wykaż prawdziwość twierdzenia Pitagorasa, korzystając z instrukcji:
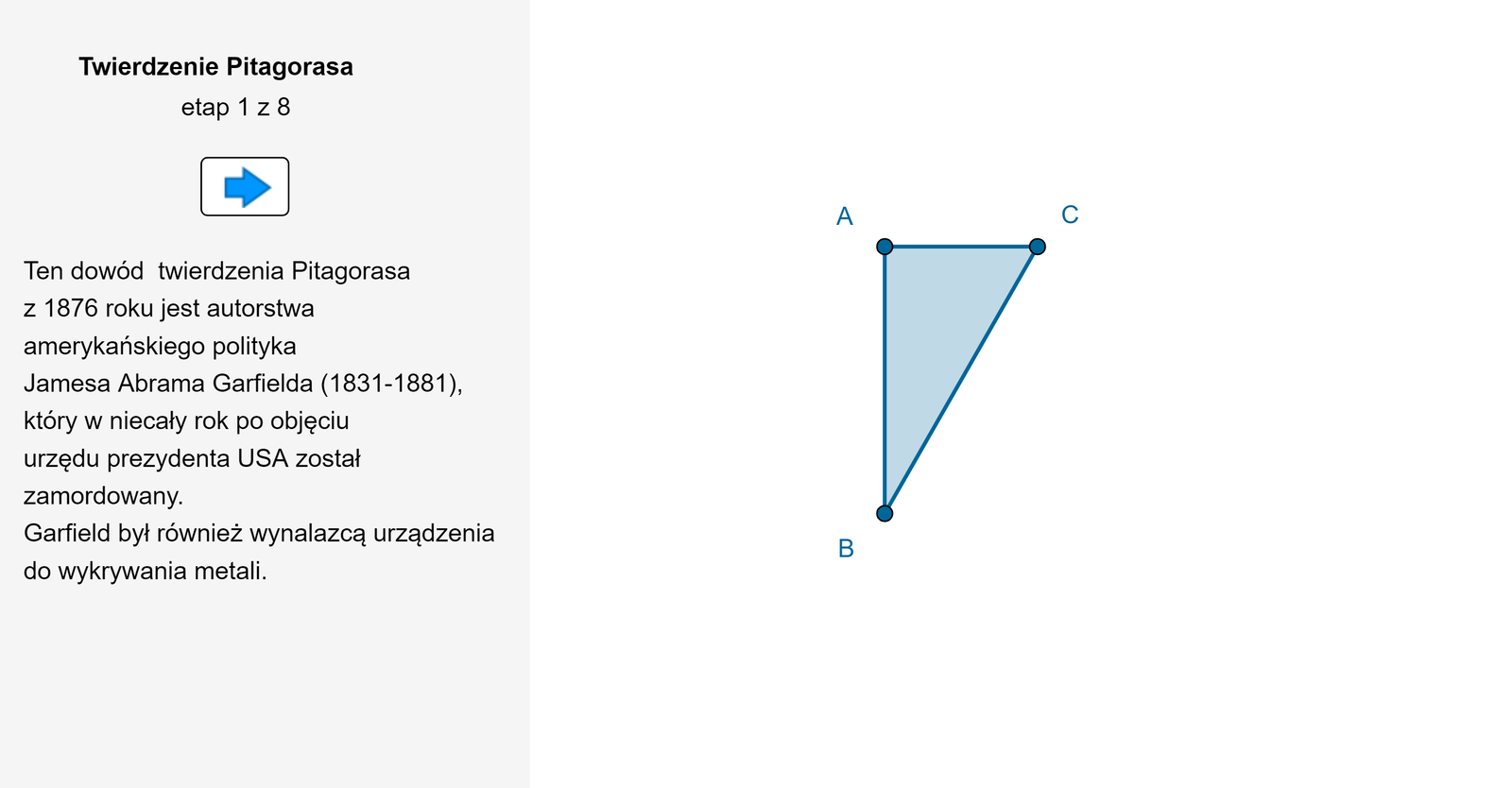
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBjZXFhOL
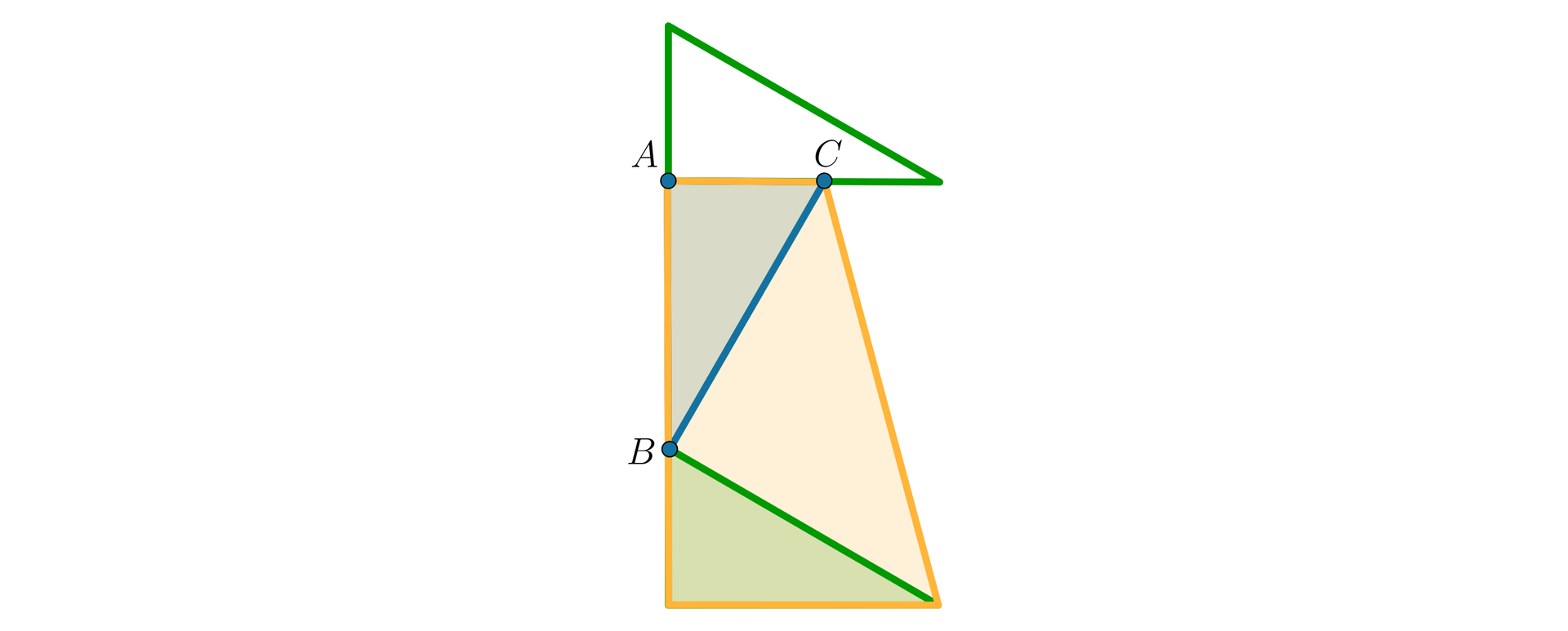
z trójkątów na rysunku zbuduj trapez
oblicz pole trapezu jako sumę pól trójkątów
oblicz pole trapezu, korzystając z odpowiedniego wzoru
porównaj otrzymane wyrażenia
sprowadź do najprostszej postaci zapisaną równość
wyciągnij wniosek
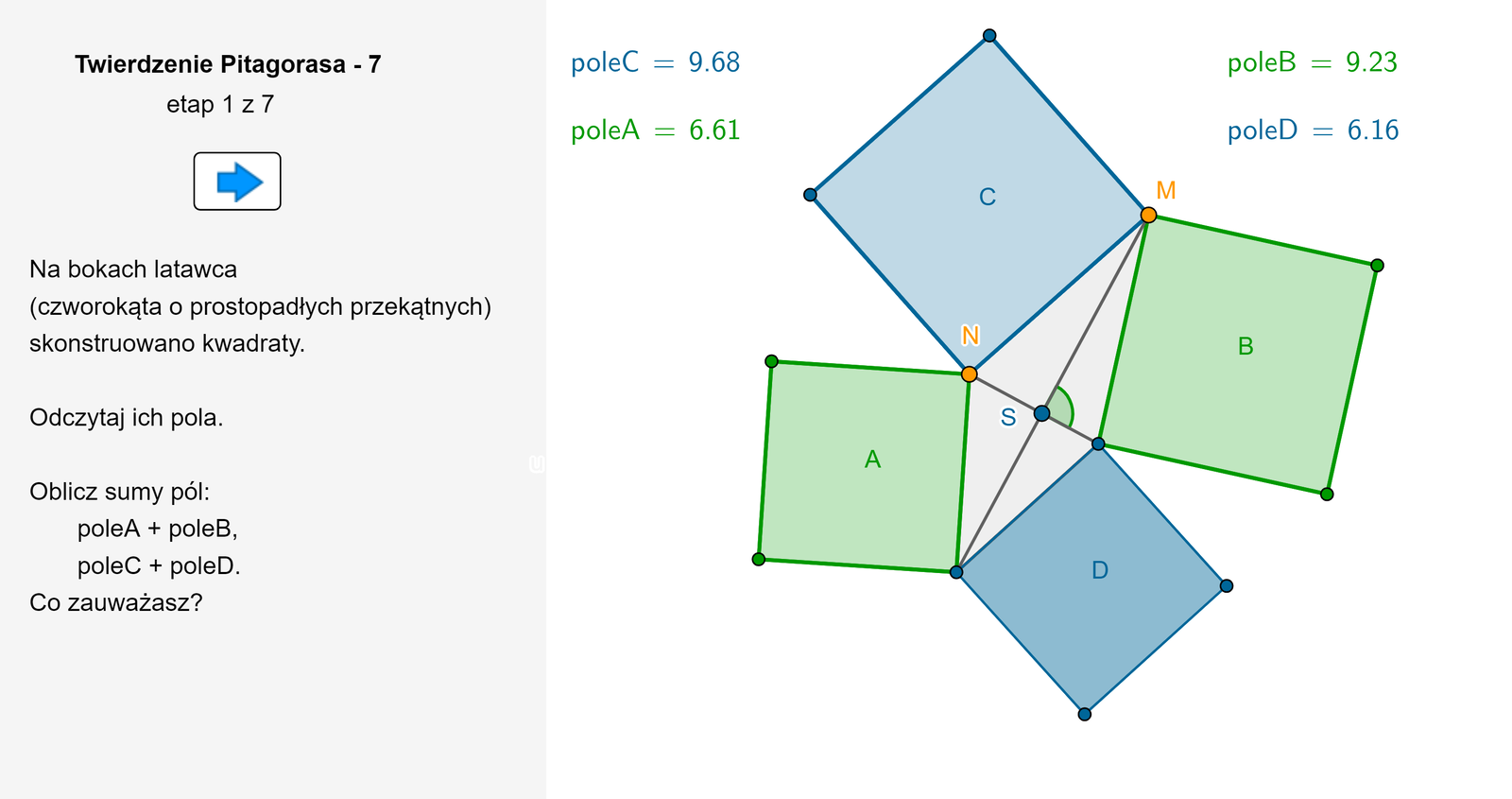
Rysunek przedstawia deltoid (latawiec), czyli czworokąt, którego przekątne są prostopadłe. Na bokach latawca zbudowano kwadraty.
Zmieniaj położenie punktu , również tak, aby uzyskać trójkąt prostokątny. W każdym przypadku porównuj sumy pól kwadratów leżących naprzeciw siebie. Co zauważasz?
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBjZXFhOL
Dokończ zdanie, wybierając poprawną odpowiedź.
Wynika z tego, że średnia arytmetyczna długości wszystkich boków trójkąta jest równa: Możliwe odpowiedzi: 1. , 2. , 3. , 4.
Dokończ zdanie, wybierając poprawną odpowiedź.
Jeden z boków trójkąta wyraża się liczbą, która nie jest wymierna, gdy: Możliwe odpowiedzi: 1. , , 2. , , 3. , , 4. ,
Losujemy dwie liczby naturalne , ze zbioru liczb naturalnych od do . Liczby
, są długościami przyprostokątnych trójkąta. Znajdź długość przeciwprostokątnej dla trzech przykładowych par wylosowanych liczb.
Zapoznaj się z apletem przedstawiającym trójkąt niespełniający założeń twierdzenia Pitagorasa.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/PBjZXFhOL