Elektrotechnika
MEC.03. Montaż i obsługa maszyn i urządzeń - Mechanik - Monter maszyn i urządzeń 723310
Podstawy elektrotechniki dla mechaników
ATLAS INTERAKTYWNY W 2D/3D
Wszystkie nagrania są tożsame z treścią poniżej.
Atom jest najmniejszą niepodzielną częścią pierwiastka zachowującą jego właściwości. Składa się on z jądra zbudowanego z posiadających pewien ładunek protonów i elektronów oraz z obojętnie elektrycznych neutronów.
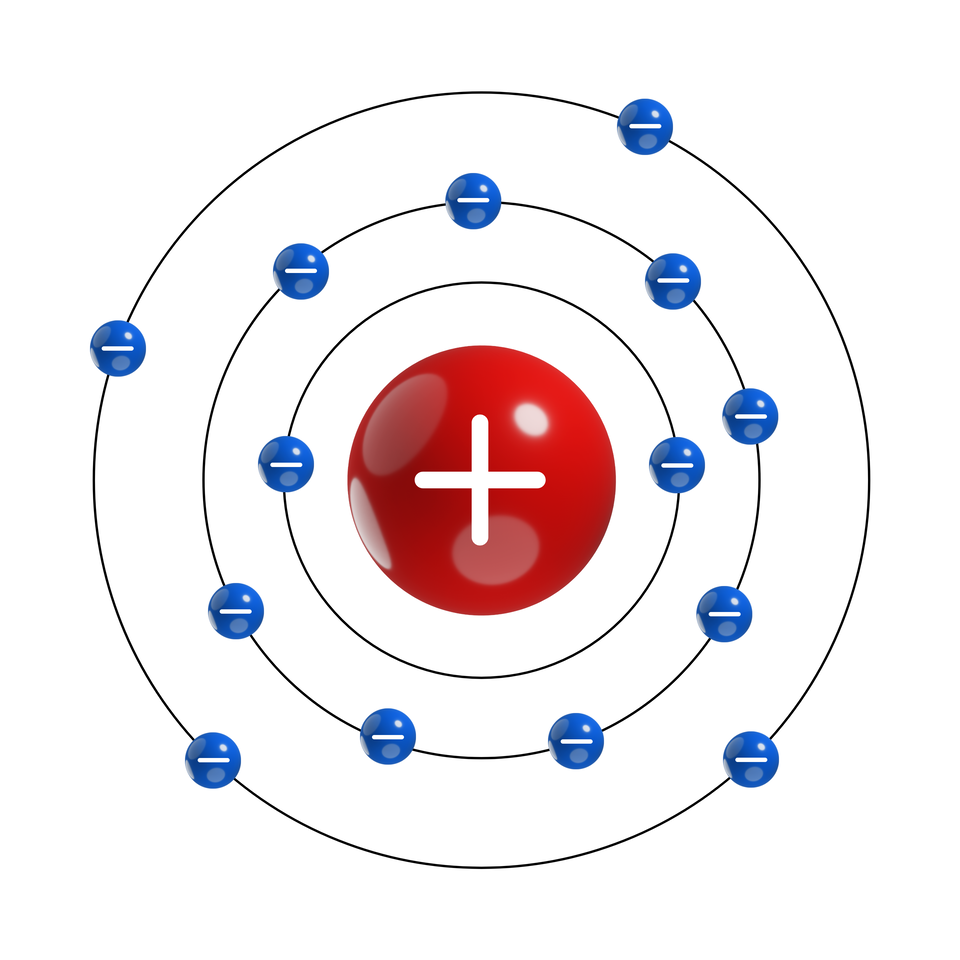
Protony są to cząstki posiadające dodatni ładunek elektryczny.
Elektrony są to cząstki posiadające ujemny ładunek elektryczny.
Ładunek elektryczny jest to pewna liczba ładunków elementarnych dodatnich lub ujemnych, za ładunek elementarny należy rozumieć ładunek elektryczny elektronu, który nie jest podzielny. Jednostką ładunku elektrycznego jest kulomb , którą można interpretować jako iloczyn jednostki natężenia prądu elektrycznego i jednostki czasu .
Zgodnie z powyższą definicją odbierając z atomu elektron, doprowadzimy do ich niedoboru, powodując tym samym iż atom stanie się naładowany dodatnio. Jeżeli jednak do atomu dostarczymy dodatkowy elektron, spowoduje to iż ten będzie posiadał ładunek ujemny z powodu nadmiaru elektronów.
Atom lub cząsteczki, które posiadają nadmiar lub niedobór elektronów w stosunku do protonów, a więc zawierających ładunek elektryczny, nazywane są jonami.
Jony dzielimy na:
Aniony są to atomy lub cząsteczki naładowane ujemnie,
Kationy są to atomy lub cząsteczki naładowane dodatnio.
Pole elektryczne jest rozumiane jako pole powstałe w przestrzeni otaczającej ładunek i objawiające się tym iż na ciała, które się w nim znajdują działa siła.
Jedną z najważniejszych wielkości charakteryzujące pole elektryczne jest:
Natężenie pola elektrycznego jest to wielkość wektorowa charakteryzująca pole elektryczne, którą definiuje się jako stosunek siły pola działającego na umieszczony w badanym polu elektrycznym ładunek próbny, do wartości tego ładunku.
Ładunkiem próbnym uznaje się ładunek , którego wytworzone pole jest na tyle słabe iż nie zakłóca ono w żaden sposób badanego pola elektrycznego .
gdzie:
to siła działająca na ładunek próbny ,
to wartość ładunku próbnego.
Jednostką natężenia pola elektrycznego jest niuton na kulomb , . Na jej podstawie możemy również wyznaczyć jednostkę wolt na metr , która jest z nią równoważna.

Linie sił pola elektrycznego są reprezentacją graficzną toru, jaki zakreśla ładunek próbny, poruszany prze siłę pola elektrycznego, w którym się znajduje. Umożliwiają one zwizualizowanie pola elektrycznego.
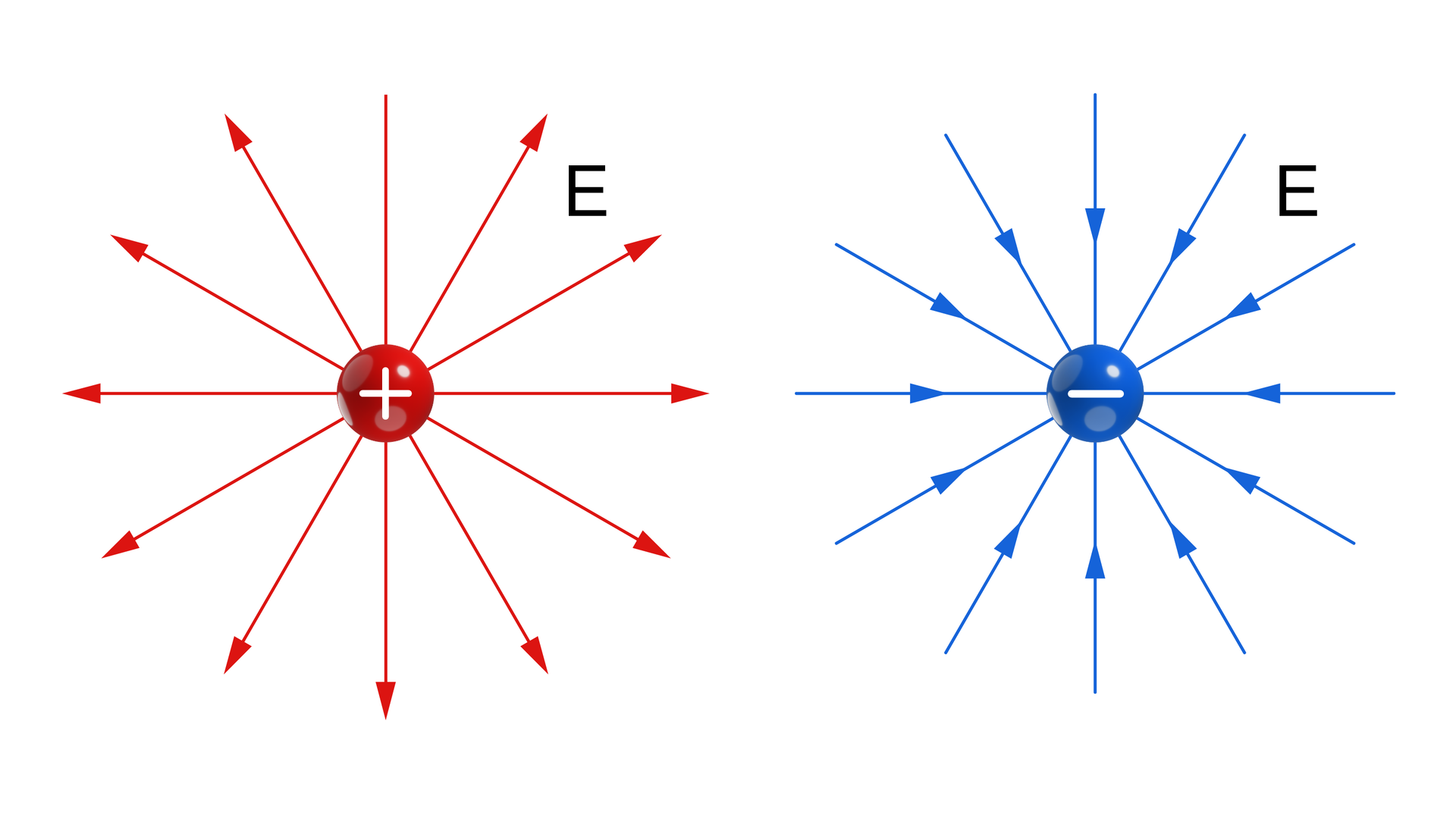
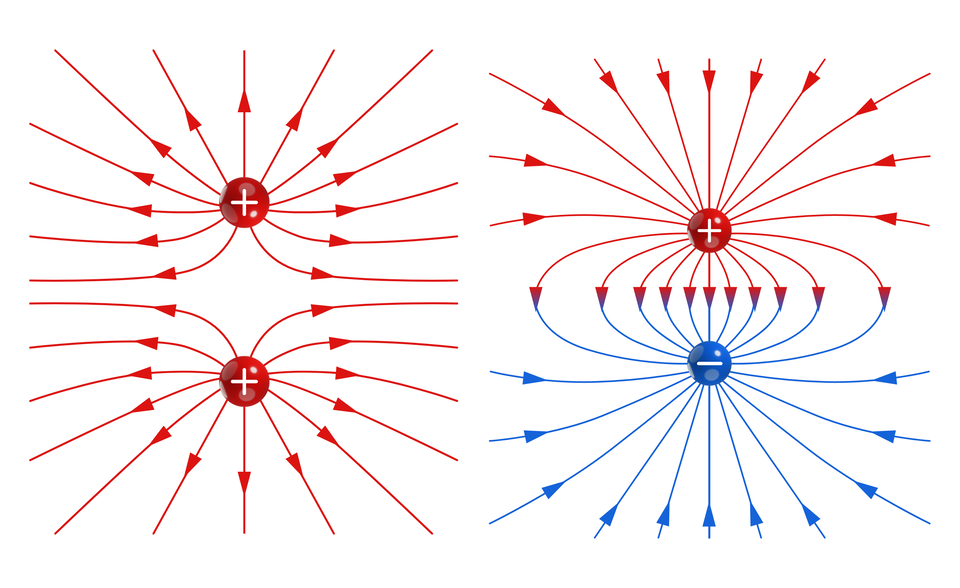
Potencjał elektryczny w określonym punkcie jest to stosunek pracy niezbędnej do przeniesienia ładunku próbnego z rozpatrywanego punktu do punktu znajdującego się w nieskończoności od ładunku próbnego . Potencjał w danym punkcie można określić wzorem:
Napięcie elektryczne występujące pomiędzy określonymi punktami oraz , które są wyrażone jako potencjały oraz , jest różnicą tych potencjałów. Jednostką napięcia elektrycznego jest wolt .
Prąd elektryczny jest to wywołany działaniem pola elektrycznego, uporządkowany ruch ładunków elektrycznych, jaki występuje w przekroju poprzecznym przewodnika.
Natężeniem prądu elektrycznego nazywamy stosunek ładunku jaki zostanie przeniesiony przez przekrój poprzeczny przewodnika, w ciągu czasu .
gdzie:
to ładunek przepływający przez przewodnik,
to czas.
Jednostką natężenia prądu elektrycznego jest amper .
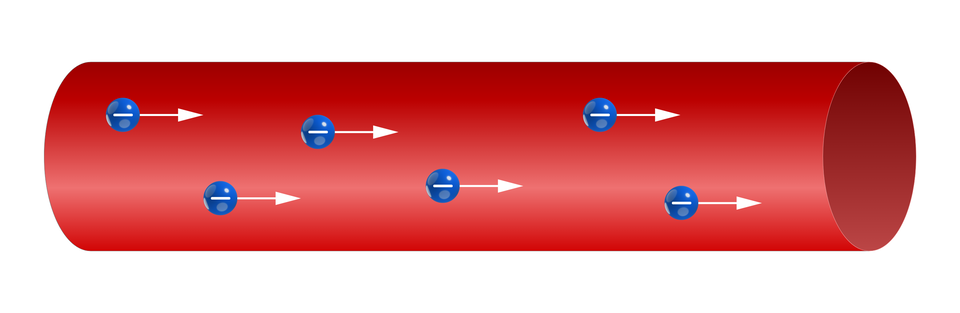
Prąd elektryczny możemy podzielić na:
Prąd stały występuje w momencie gdy natężenie prądu elektrycznego przepływającego przez przewodnik nie zmienia się w funkcji czasu.
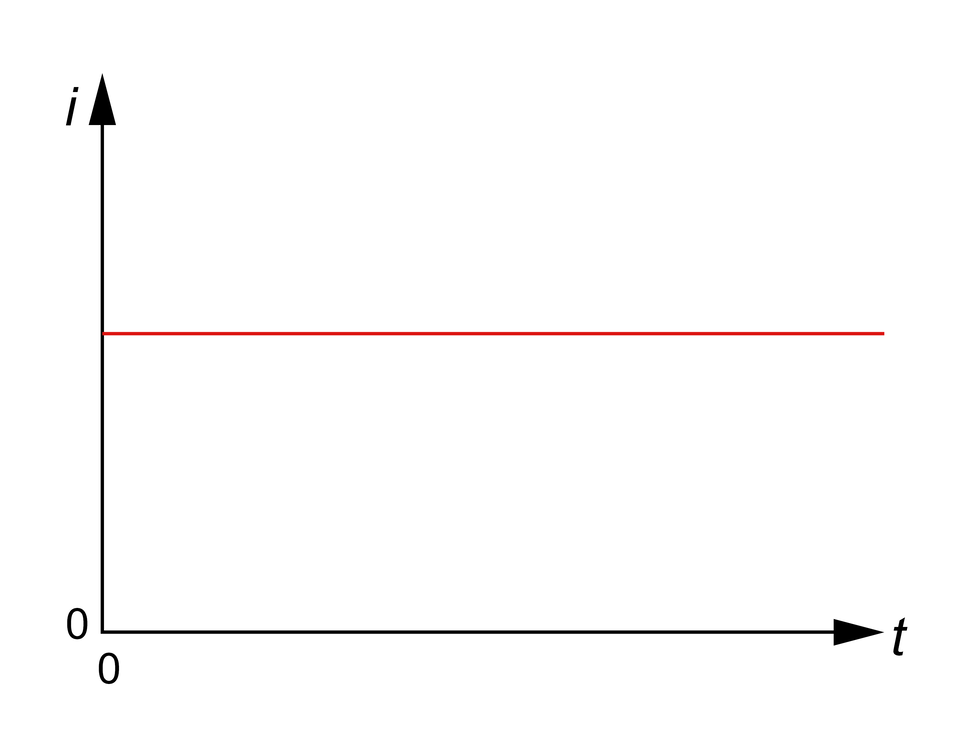
gdzie:
to chwilowe natężenie produ,
to czas.
Prąd zmienny występuje w momencie gdy natężenie prądu elektrycznego przepływającego przez przewodnik zmienia się w funkcji czasu.
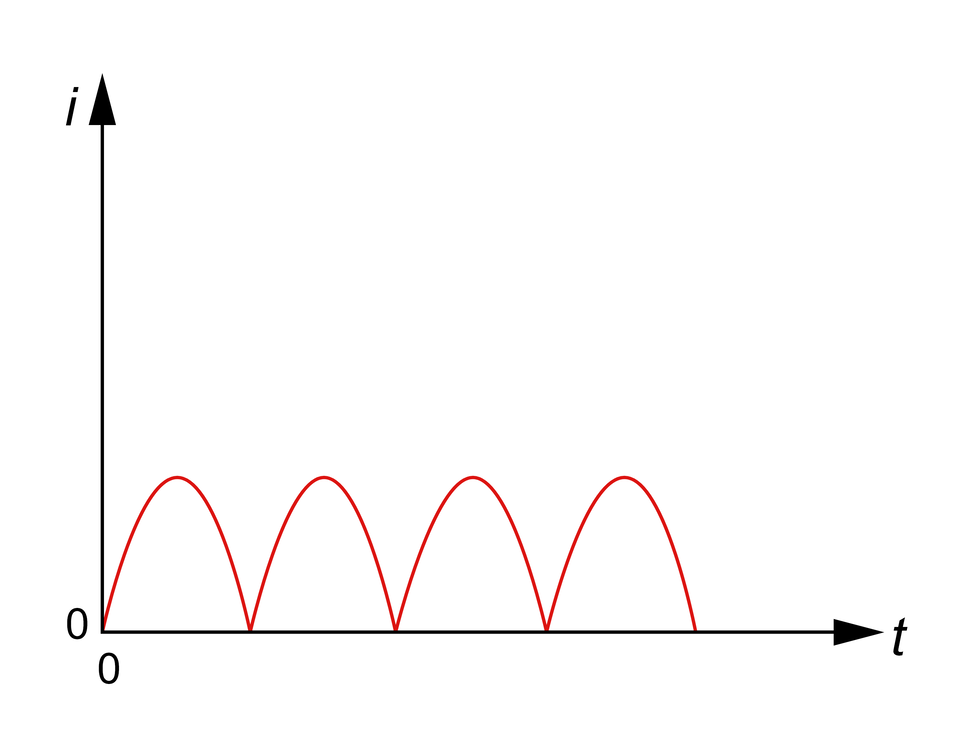
gdzie:
to chwilowe natężenie produ,
to czas.
Prąd przemienny jest to rodzaj prądu zmiennego, w który oprócz zmiany jego natężenia w funkcji czasu, następuje okresowa zmiana jego wartości na przeciwny.
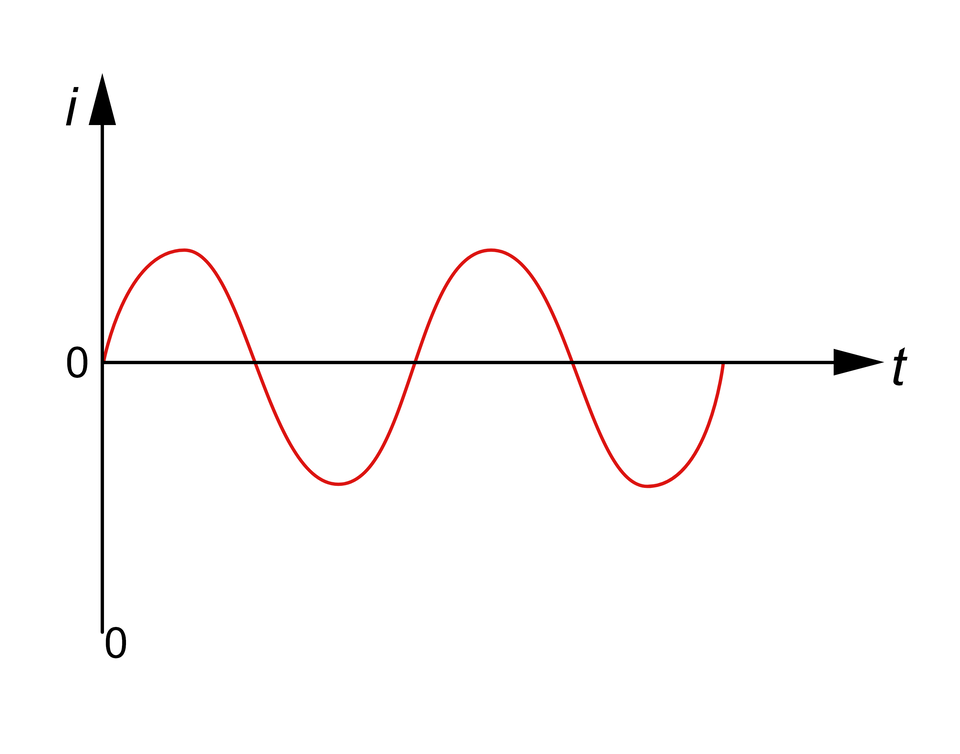
gdzie:
to chwilowe natężenie produ,
to czas.
Źródłem energii elektrycznej nazywany przetworniki energii umożliwiające zamianę jednej z postaci energii na energię elektryczną. Zazwyczaj są to procesy dwukierunkowe (umożliwiające również transformację energii elektrycznej na energię pierwotnie przetworzoną).
Wyróżniamy różne rodzaje źródeł energii elektrycznej, do najważniejszych zaliczamy:
źródła elektromechaniczne,
źródła chemiczne,
źródła cieplne,
źródła świetlne.
Źródła elektromechaniczne
Są to przetworniki umożlwiające zamianę energii mechanicznej na energię elektryczną. W zależności od swojej budowy, można je podzielić na:
źródła prądu stałego,
źródła prądu przemiennego.
Generatory znajdują szerokie zastosowanie w elektrowniach konwencjonalnych jaki odnawialnych źródłach energii, są one bowiem wykorzystywane m.in. w elektrowniach wodnych, wiatrowych, atomowych jak i węglowych.
Zasada działania prądnicy elektrycznej opiera się na zjawisku indukcji elektromagnetycznej. W obracającym się w zewnętrznym polu magnetycznym przewodniku, indukuje się siła elektromotoryczna . Jej wartość jest zależna od prędkości obrotowej przewodnika , jego długości oraz od wartości indukcji magnetycznej . Jednostką siły elektromotorycznej jest wolt .
gdzie:
to indukcja magnetyczna ,
to długość przewodnika ,
to prędkość obrotowa przewodnika .
Źródła chemiczne
Jednym z rodzajów chemicznych źródeł energii są ogniwa galwaniczne. Są to źródła prądu stałego, które umożliwiają również magazynowanie energii elektrycznej. Zbudowane są z dwóch elektrod (anody i katody) zanurzonych w elektrolicie.
Wytwarzanie energii elektrycznej opiera się tu na zjawiskach chemicznych. W wyniku zamknięcia obwodu ogniwa, następuje migracja jonów ujemnych (anionów), które docierają do elektrody ujemnej, oraz jonów dodatnich (kationów), które docierają do elektrody dodatniej. W wyniku tego na elektrodach ustala się różny potencjał elektryczny. Różnica potencjałów występujących między elektrodami powoduje powstanie napięcia .
gdzie:
, – Potencjał elektryczny danej elektrody .
W zależności od zastosowanych materiałów, z których wykonane są elektrody, możliwe jest uzyskanie różnych wartości napięcia na zaciskach ogniwa.
Przykładami tego rodzaju źródeł energii elektrycznej są baterie lub akumulatory.
Źródła świetlne
Generatory fotoelektryczne, są to źródła umożliwiające wytwarzanie energii elektryczne z wykorzystaniem promieniowania świetlnego. Zasada działania ogniw fotoelektrycznych opiera się na zjawisku fotowoltaicznym. W wyniku oświetlenia złącza półprzewodnikowego , fotony powodują generowanie par elektron–dziura, a więc ładunków elektrycznych. Elektrony przenoszone są w kierunku półprzewodnika typu , dziury zaś w kierunku półprzewodnika typu . W wyniku zgromadzenia się różnoimiennych ładunków w obszarze każdego typu półprzewodnika, pomiędzy nimi powstaje różnica potencjałów, która wywołuje powstanie napięcia.
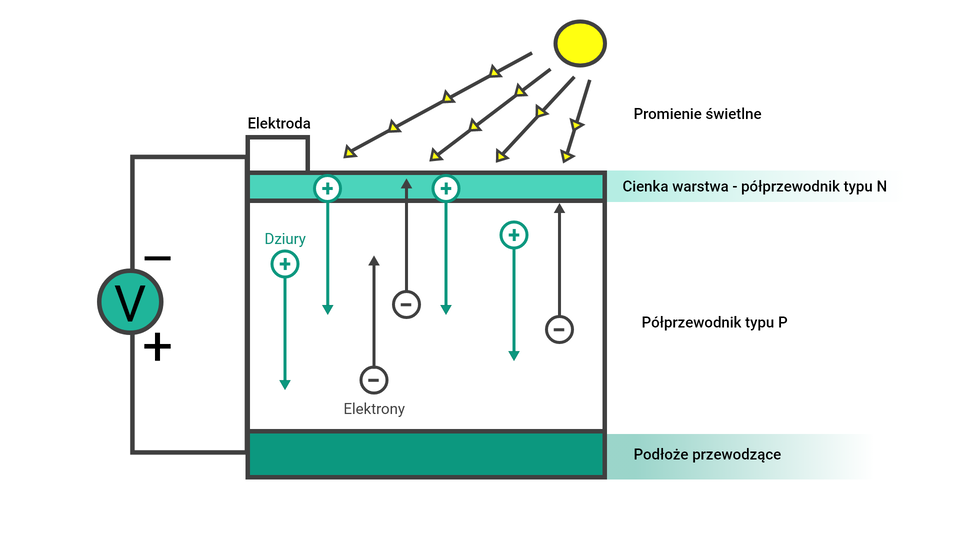
Źródła termiczne
Wykorzystanie zjawiska termoelektrycznego, umożliwia bezpośrednią przemianę energii cieplnej na energię elektryczną. Wytwarzanie napięcia odbywa się na styku dwóch różnych metali lub półprzewodników, znajdujących się w temperaturze różnej od ich pozostałej części. Jest ono wywołane różną koncentracją elektronów dla różnych materiałów, która zależy również od temperatury. W wyniku tego, na styku dwóch metali lub półprzewodników powstaje różnica potencjałów, która jest nazywana napięciem termoelektrycznym. Ten rodzaj zjawiska termoelektrycznego nazywa się również zjawiskiem Seebecka, od nazwiska jego odkrywcy. Pierwszą termoparę zbudowano z połączenia miedzi i bizmutu. Obecnie do budowy termopar stosuje się połączenia metali szlachetnych np.: połączenie wolframu i molibdenu, platyny i platynorodu, lub metale nieszlachetne np. połączenie żelazo i miedź‑nikiel, połączenie chromu i niklu. Wykorzystuje się je głównie w termoparach, umożliwiając tym samym dokładny pomiar nawet bardzo wysokich temperatur.
Napięcie występujące na zaciskach różnych materiałów określa wzór:
gdzie:
, to współczynnik Seebecka określony dla danego materiału ,
, to temperatury w jakiej znajduje się materiał .
Obwodem elektrycznym nazywamy zespół połączonych ze sobą elementów, które tworzą przynajmniej jedną zamkniętą drogę dla przepływu prądu. Wyróżniamy w nich dwa podstawowe typy elementów:
elementy źródłowe (aktywne)–doprowadzające energię elektryczną do obwodu,
elementy odbiornikowe (bierne)–rozpraszające lub akumulujące energię elektryczną.
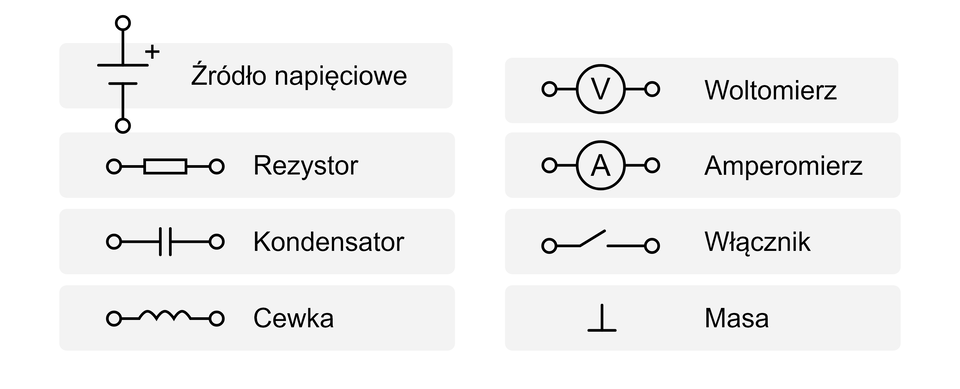
Schemat obwodu elektrycznego tworzony jest z wykorzystaniem symboli graficznych elementów źródłowych i odbiornikowych. Wykorzystywane są również symbole pomocnicze, które nie nalezą do grupy wyżej wymienionych elementów. Zaliczamy do nich m.in.: połączenia między elementami, przyrządy pomiarowe, włączniki, masa obwodu.
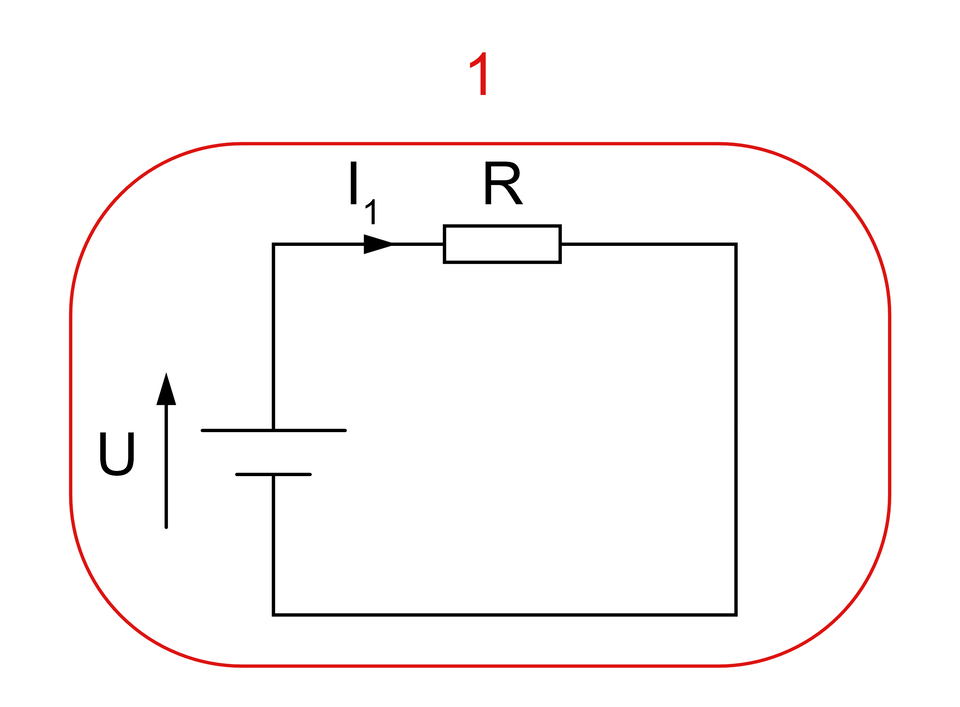
Podczas analizy obwodów elektrycznych, niezbędna jest znajomość jej charakterystycznych elementów takich jak:
Gałąź obwodu jest to część obwodu lub stanowiąca jego całość, stworzona z jednego bądź więcej elementów, które połączone są szeregowo, a więc przez wszystkie elementy wchodzące w skład gałęzi, płynie ten sam prąd elektryczny.
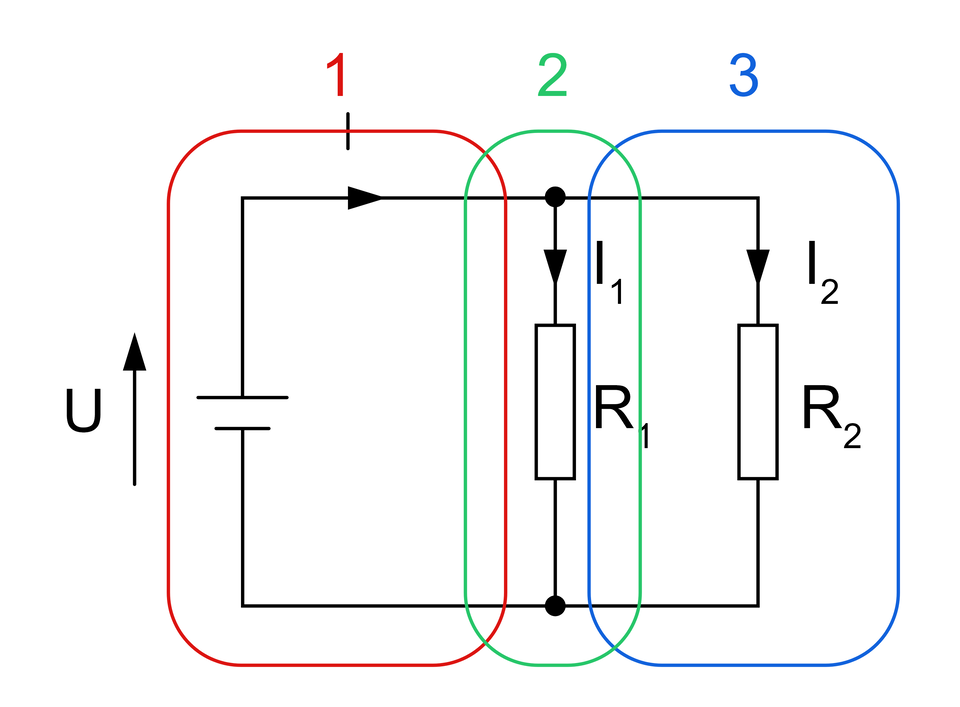
Węzeł obwodu jest to punkt w obwodzie, w którym łączą się co najmniej trzy gałęzie.
Oczko obwodu elektrycznego jest to zespół połączonych ze sobą gałęzi obwodu, które tworzą zamkniętą drogę dla przepływu pądu. Cechą charakterystyczną oczka jest to iż po usunięciu dowolnej gałęzi, pozostałe nie tworzą zamkniętej drogi obwodu.
Obwód elektryczny zawierający jedno oczko nazywamy obwodem nierozgałęzionym. Występuje w nim tylko jedna droga przepływu prądu, a co za tym idzie przez każdy element obwodu przepływa jeden i ten sam prąd.
Jeżeli obwód zawiera przynajmniej dwa oczka, to ten nazywany jest obwodem rozgałęzionym.
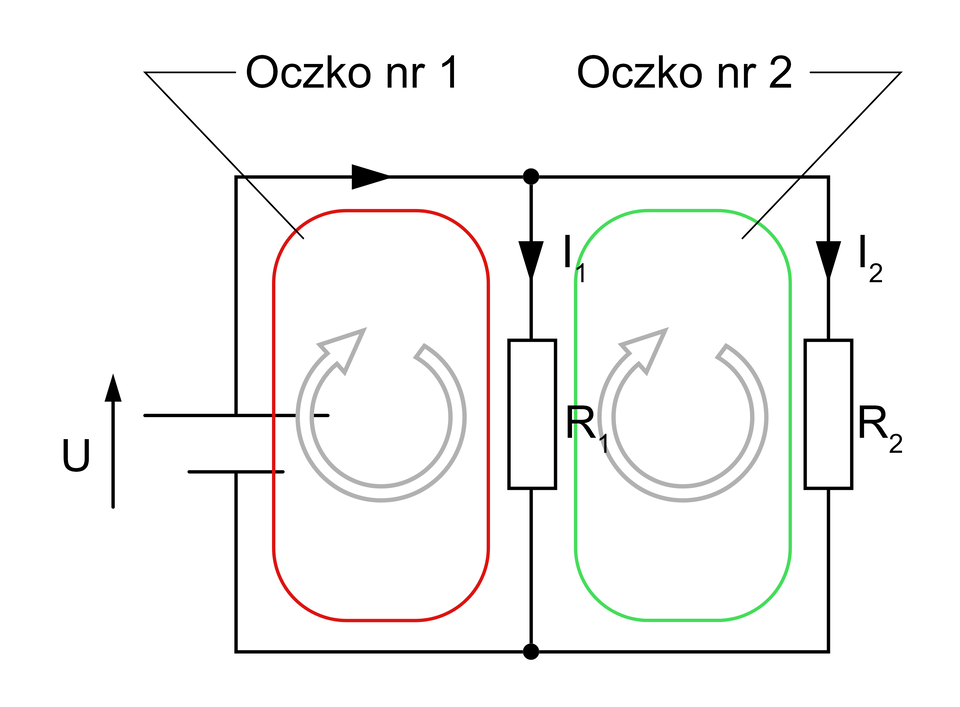
Podczas analizy obwodów elektrycznych, bardzo ważnym elementem jest odpowiednie znakowanie zwrotu prądu oraz polaryzacji napięcia na schematach elektrycznych. Realizowane jest to z wykorzystaniem przyjętych zasad strzałkowania.
Znakowanie napięcia
Znakowanie napięcia na schematach elektrycznych realizuje się poprzez umieszczenie strzałki w pobliżu elementów źródłowych lub odbiornikowych. Grot strzałki zawsze wskazuje zacisk, na którym występuję wyższy potencjał. Elementy źródłowe są często dodatkowo oznaczane znakiem „” oraz „”, tak więc grot strzałki określającej polaryzację napięcia elementu źródłowego, skierowany jest w stronę znaku „”.
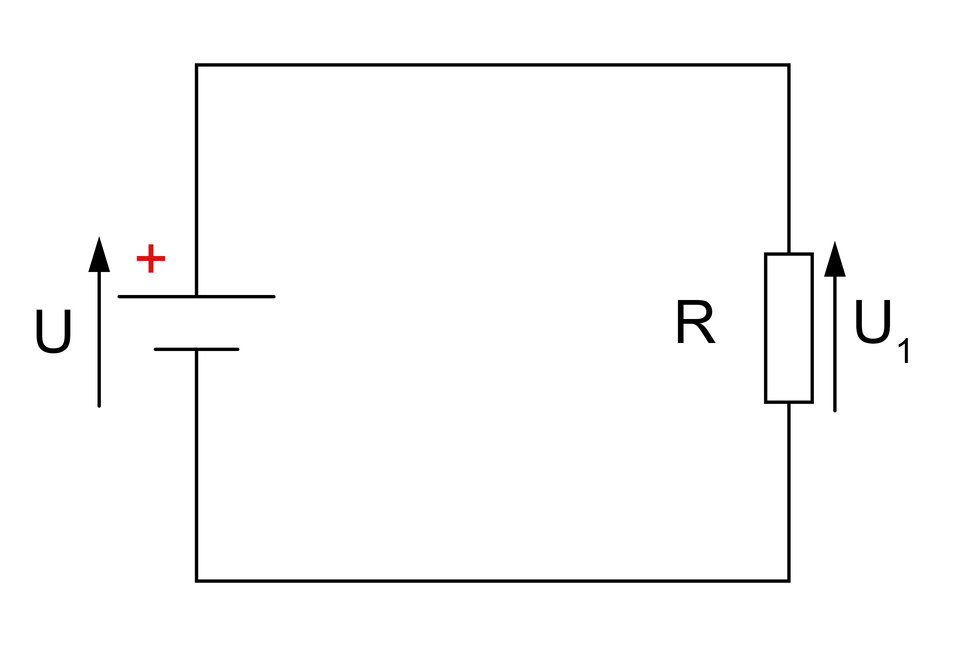
Znakowanie prądu
Oznaczanie kierunku przepływu prądu odbywa się poprzez naniesienie strzałki bezpośrednio na gałąź obwodu, przez którą następuje jego przepływ. Umownie przyjęło się, że strzałka nanoszona jest od zacisku o wyższym potencjale do zacisku o niższym potencjale. Według przyjętych zasad znakowania, strzałki prądu oraz grot strzałki napięcia są skierowane do siebie w sposób zgodny na elementach źródłowych oraz przeciwnie na elementach odbiornikowych.
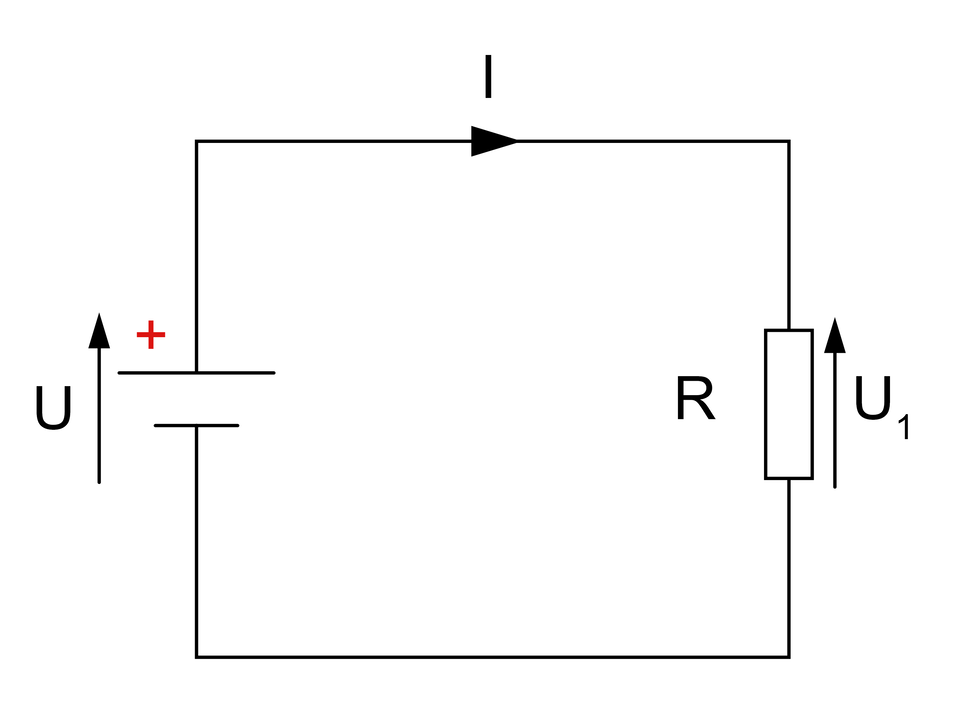
Połączenie szeregowe
Jest to jedna z metod łączenia elementów źródłowych i odbiornikowych, w której elementy łączone są kolejno po sobie tworząc tym samym połączenie o jednej gałęzi obwodu. Połączenie to charakteryzuje się tym, iż przez wszystkie jej elementy przepływa ten sam prąd.
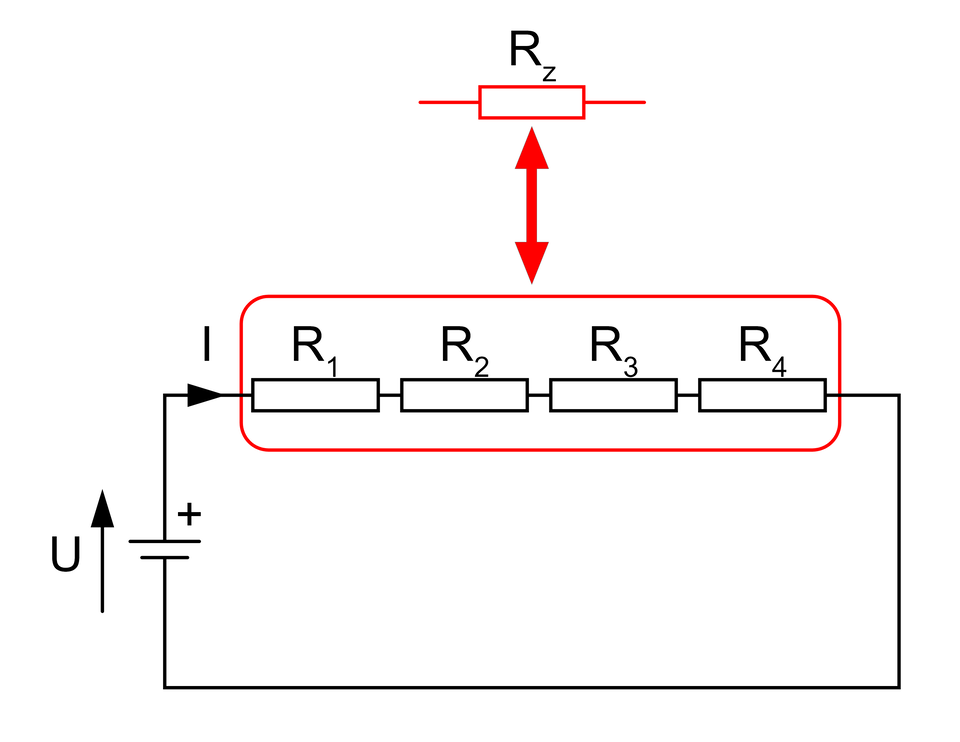
Dla połączenia szeregowego, możliwe jest przekształcenie połączonych ze sobą szeregowo elementów, na rezystancję zastępczą wyrażoną wzorem:
Powyższy obwód elektryczny możemy uprościć, zastępując go obwodem równoważnym, w którym wszystkie rezystancje składowe zostają przekształcone na rezystancję zastępczą, zgodnie ze wzorem:
Połączenie równoległe
Jest to sposób łączenia elementów źródłowych i odbiornikowych, gdzie wszystkie elementy włączone w obwód, tworzą parę zacisków, gdzie każdy jej końców posiada ten sam potencjał. Napięcie na poszczególnych elementach obwodu jest jednakowe i przyjmuje ono wartość napięcia zasilającego.
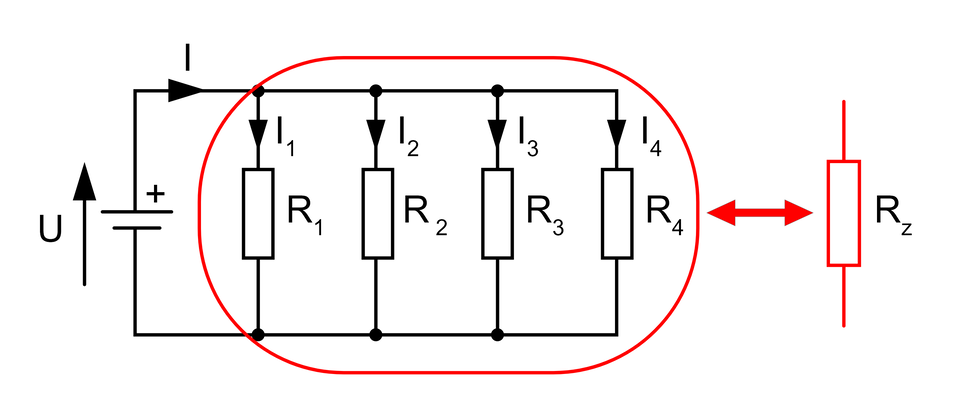
Dla połączenia równoległego, możliwe jest przekształcenie połączonych ze sobą równolegle elementów, na odwrotność rezystancji zastępczej wyrażoną wzorem:
Powyższy obwód elektryczny możemy uprościć, zastępując go obwodem równoważnym, w którym wszystkie rezystancje składowe zostają przekształcone na odwrotność rezystancji zastępczej, zgodnie ze wzorem:
Prawo Ohma jest jednym z podstawowych praw wykorzystywanych w elektrotechnice. Opisuje ono proporcjonalność natężenia prądu w danym przewodniku do napięcia występującego na jego zaciskach. Można go przedstawić z wykorzystaniem wzoru:
gdzie:
to napięcia na danym elemencie ,
to natężenie prądu przepływającego przez dany element ,
to rezystancja elementu .
Wzór można przekształcić do postaci:
lub
Powyższy wzór umożliwia obliczenie rezystancji danego elementu mierzonej w omach , wykorzystując w tym celu wartość napięcia występującego na danym elemencie oraz natężenia prądu jaki przez niego przepływa.
Przykład 1
Wykorzystując prawo Ohma, oblicz wartość natężenia prądu , mając do dyspozycji dane:
,
.
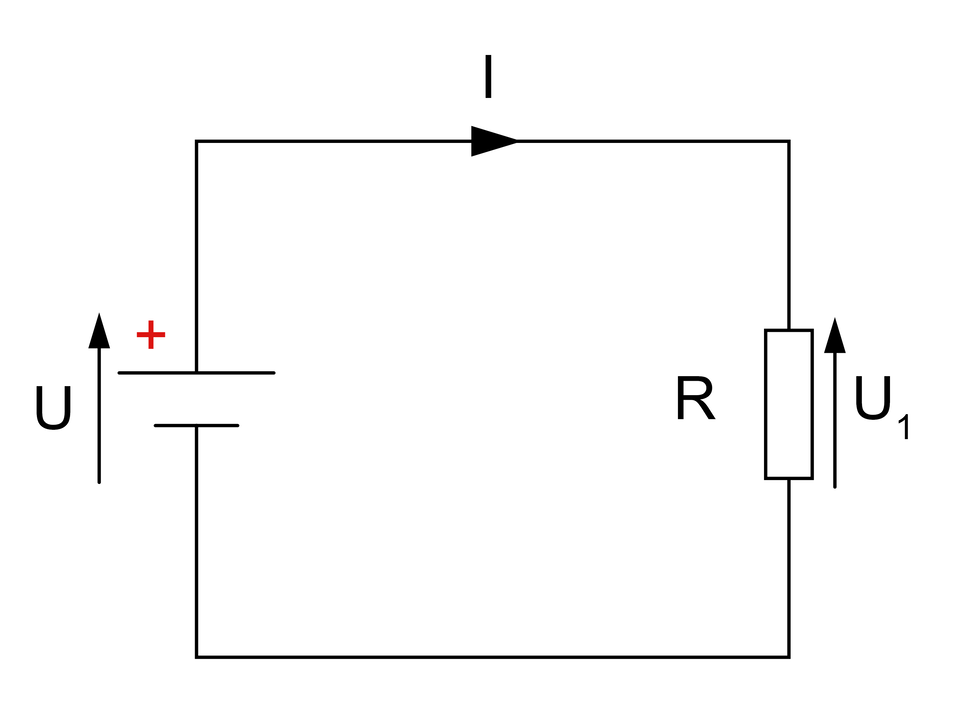
Elementem odbiornikowym w powyższym obwodzie jest rezystor , który jest włączony w sposób równoległy do źródła. Oznacza to iż na zaciskach rezystora występuje takie samo napięcie co na zaciskach źródła napięciowego.
Etap 1: Obliczanie wartości natężenia prądu .
.
Przykład 2
Wykorzystując prawo Ohma oblicz wartość natężenia prądu oraz wartość napięć oraz , mając do dyspozycji dane:
,
,
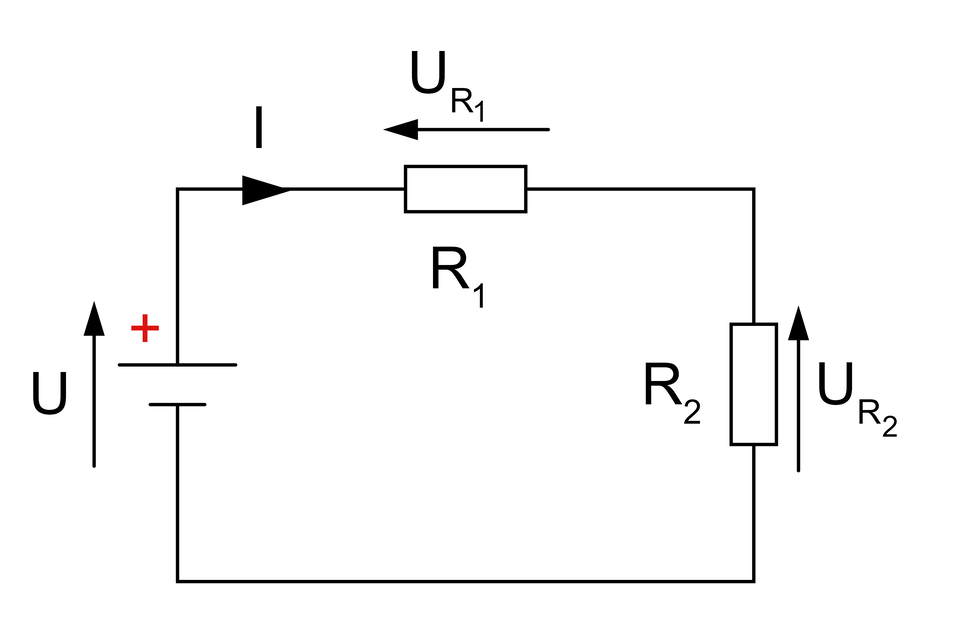
Etap 1: Obliczanie sumarycznej wartości rezystancji obciążenia
W celu wyznaczenia prądu pobieranego ze źródła, niezbędna jest znajomość wartości rezystancji zastępczej jego obciążenia, stąd pierwszym etapem jest obliczenie tzw. rezystancji zastępczej :
.
Powyższa wartość umożliwia nam uproszczenie obwodu do postaci:
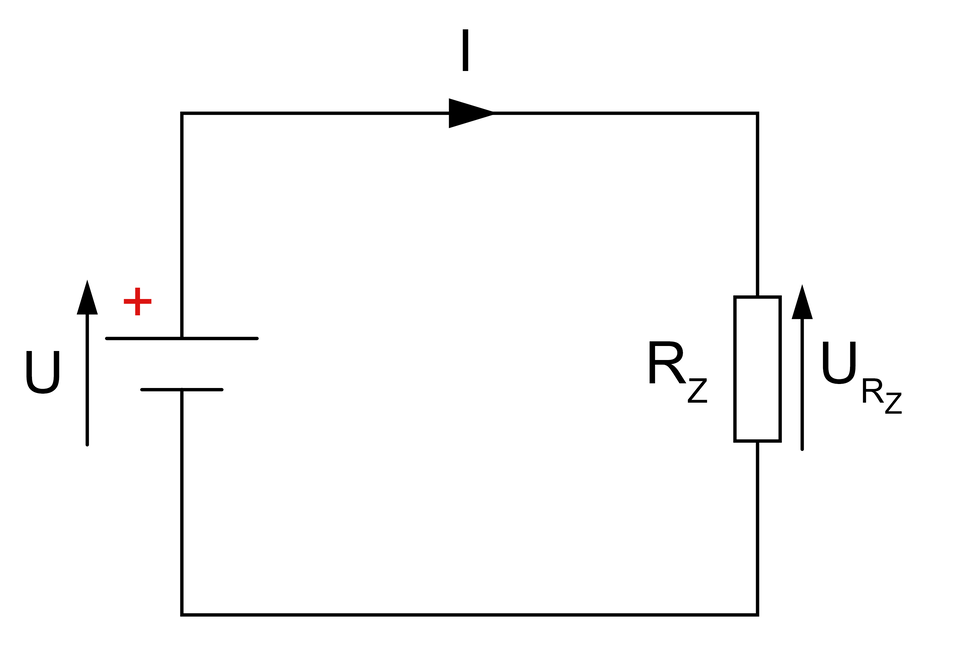
Etap 2: Obliczanie wartości natężenia prądu
.
Etap 3: Obliczanie wartości napięć oraz .
Znając już wartość natężenia prądu, możemy powrócić do pierwotnego schematu obwodu oraz wyznaczyć wartości napięć na poszczególnych rezystorach:
.
Ze względu na jednakową wartość rezystancji elementów oraz możemy przyjąć:
.
Prawa Kirchhoffa są podstawowymi prawami obok prawa Ohma wykorzystywanymi w elektrotechnice, przy analizie obwodów elektrycznych.
Pierwsze prawo Kirchhoffa nazywane również prądowym prawem Kirchhoffa, jest zdefiniowane następująco:

Zgodnie z definicją pierwszego prawa Kirchhoffa, bilans prądów dla powyższego węzła możemy zapisać w postaci:
.
Jeżeli zwrot strzałki prądowej jest skierowany w kierunku węzła, wtedy wielkość podstawiamy do równania ze znakiem „”. Jeżeli jednak grot strzałki jest skierowany od węzła, wtedy w równaniu zapisujemy wartość prądu ze znakiem
„”.
W momencie gdy w obwodzie występuje kilka elementów źródłowych, nie jesteśmy w stanie określić rzeczywistego kierunku przepływu prądu. W takich przypadkach podczas znakowania prądów, ich zwrot nadajemy w sposób umowny.
Drugie prawo Kirchhoffa nazywane również napięciowym prawem Kirchhoffa jest zdefiniowane następująco:
Suma napięć źródłowych oraz suma napięć odbiornikowych dla analizowanego oczka jest równa zeru.
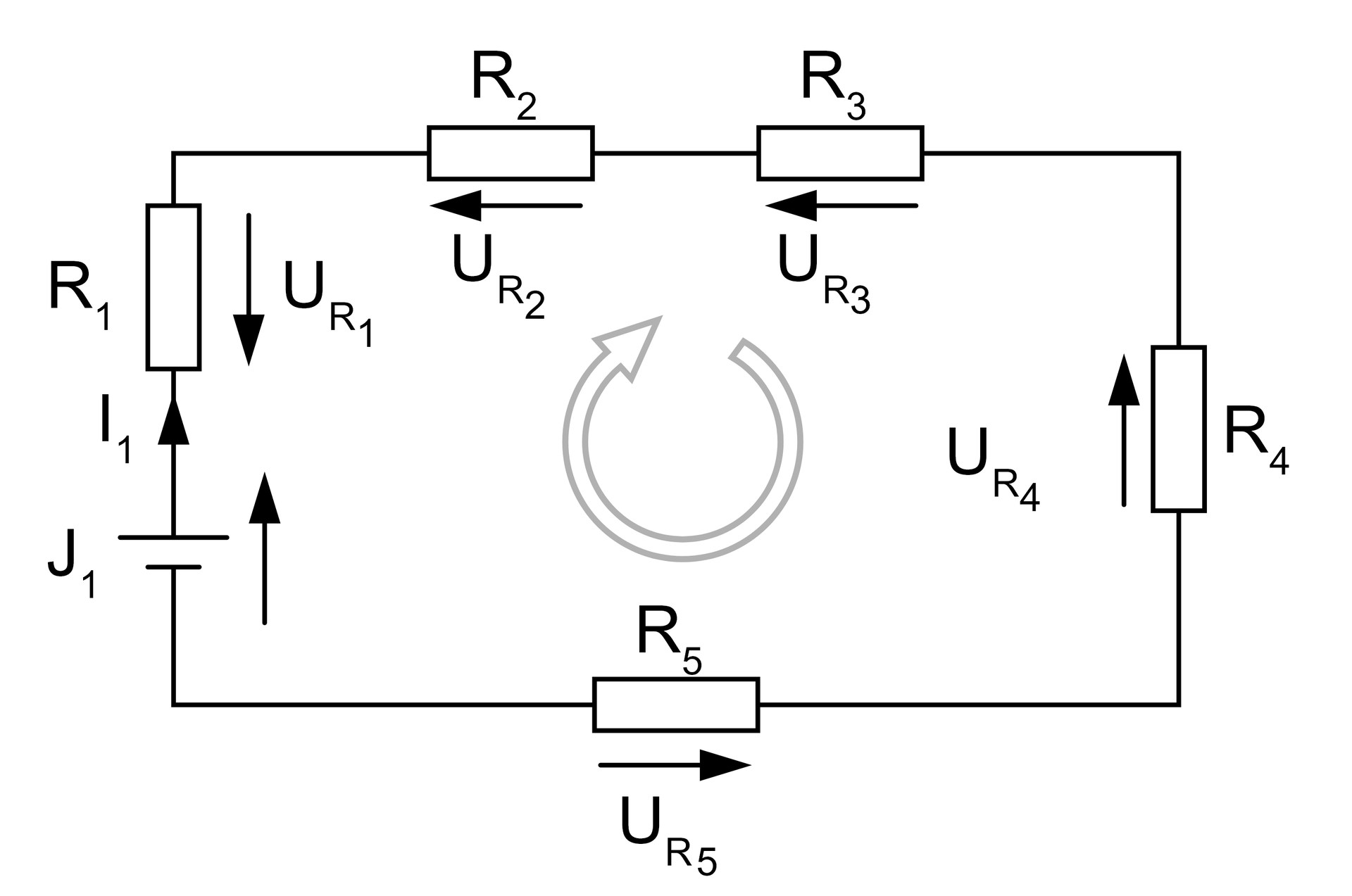
Zgodnie z powyższą definicją napięciowego prawa Kirchhoffa, bilans napięć powyższego węzła możemy zapisać w postaci:
.
Strzałka umieszczona w środku oczka informuje o kierunku jego obiegu. Jej kierunek jest umowy i nie wpływa na wynik bilansu napięć. Jeżeli zwrot strzałki obiegu oczka jest zgodny ze zwrotem strzałki napięciowej elementu, to jego napięcie podstawiamy do równania ze znakiem „”. Gdy zaś zwrot strzałek jest przeciwny, wtedy napięcie, jakie znajduje się na elemencie zapisujemy ze znakiem „”.
Przykład 1
Wykorzystują pierwsze oraz drugie prawo Kirchhoffa, wyznacz wartości prądów , , , mając do dyspozycji dane:
,
,
,
,
,
.
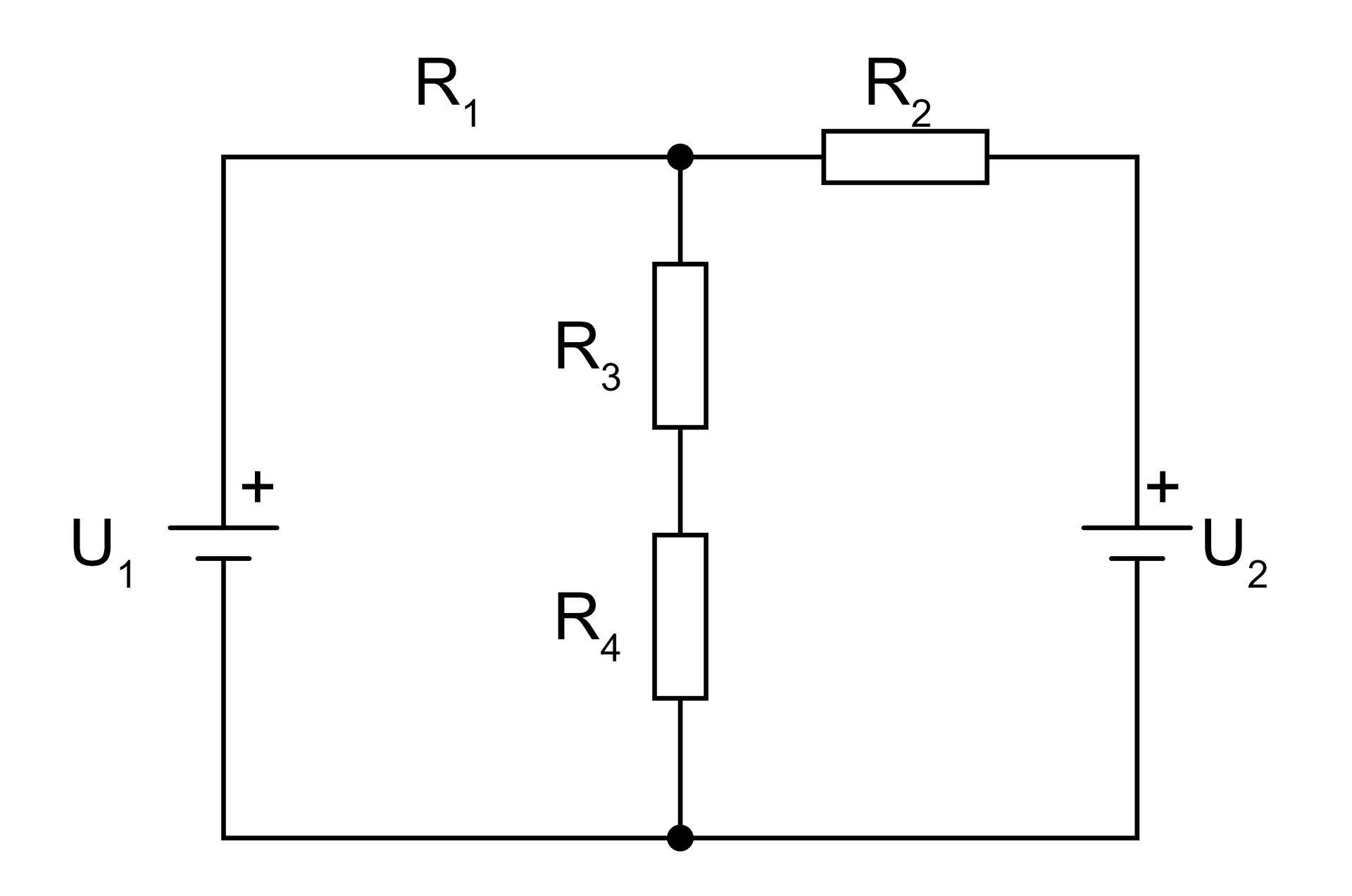
Etap 1: Ustalenie kierunku obiegu oczka oraz znakowanie prądów i napięć.
Powyższy układ składa się z dwóch oczek, gdzie dla każdego z nich przyjmujemy kierunek obiegu oczka w prawo.
Ze względu iż obwód posiada dwa źródła napięciowe, nie jesteśmy w stanie określić rzeczywistego kierunku przepływu prądu, dlatego ich zwrot zostaje przyjęty w sposób dowolny.

Etap 2: Zapis równania bilansów prądów oraz napięć wg prawa Kirchhoffa
Prądowe prawo Kirchhoffa:
.
Napięciowe prawo Kirchhoffa:
Oczko nr :
.
Wyznaczając , daje nam postać:
.
Oczko nr :
.
Wyznaczając , daje nam postać:
.
Etap 3: Przekształcenie napięć odbiornikowych na iloczyn rezystancji i prądu, zgodnie z prawem Ohma.
Oczko nr :
.
Oczko nr :
.
Etap 4: Podstawianie wartości do równania.
Oczko nr :
.
Oczko nr :
.
Co jest równoważne z:
Oczko nr :
.
Oczko nr :
.
Dzieląc oba równania przez , otrzymujemy:
Oczko nr :
.
Oczko nr :
.
Etap 5: Rozwiązywanie układu równań
Podstawiamy za wartość , sumę prądów oraz , wynikającą z wcześniej wyznaczonego bilansu prądów, zgodnego z prądowym prawem Kirchhoffa
Mnożymy górne równanie przez :
Dodajemy stronami równanie:
.
Wyznaczamy wartość :
.
Podstawiamy obliczoną wartość do jednego z powyższych równań i wyznaczamy wartość prądu :
,
,
.
Obliczona wartość prądu , jest ujemna co oznacza, że założony na początku analizy, kierunek przepływu prądu jest różny od kierunku rzeczywistego.
Wyznaczamy prąd , wykorzystując równanie prądowego prawa Kirchhoffa:
,
,
.
Podobnie jak w przypadku prądu , uzyskaliśmy wartość ujemna co oznacza, iż rzeczywisty kierunek prądu jest przeciwny do założonego.
Kondensator jest to bierny element elektroniczny, którego charakterystyczna cechą jest gromadzenie energii elektrycznej. Zbudowany jest z dwóch przewodników zwanych okładkami, które oddzielone są od siebie materiałem dielektrycznym. Przykładowo dla kondensatorów foliowych okładzinami mogą być dwa kawałki folii aluminiowej przedzielone dielektrykiem – folią propylenową. Dla zmniejszenia rozmiarów okładziny z dielektrykiem są ciasno zawijane tworząc kształt cylindra.
Zdolność gromadzenia ładunku elektrycznego przez kondensator nazywana jest pojemnością kondensatora, która wyrażona jest jako stosunek zgromadzonego ładunku na jego okładkach, do przyłożonego do nich napięcia. Jednostką pojemności kondensatora jest farad .
gdzie:
to pojemność kondensatora ,
to ładunek elektryczny ,
to napięcie elektryczne .
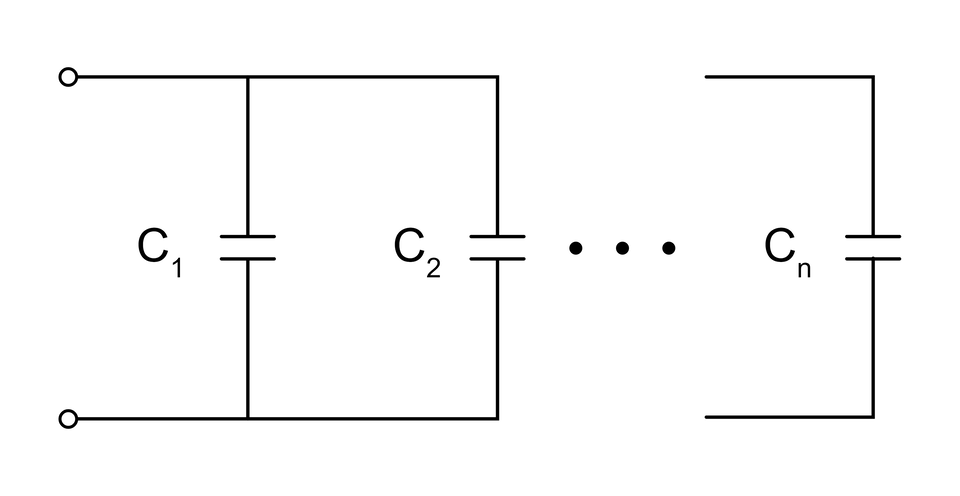
Połączenie równoległe
Dla połączenia równoległego, możliwe jest przekształcenie połączonych ze sobą równolegle elementów, na pojemność zastępczą wyrażoną wzorem:
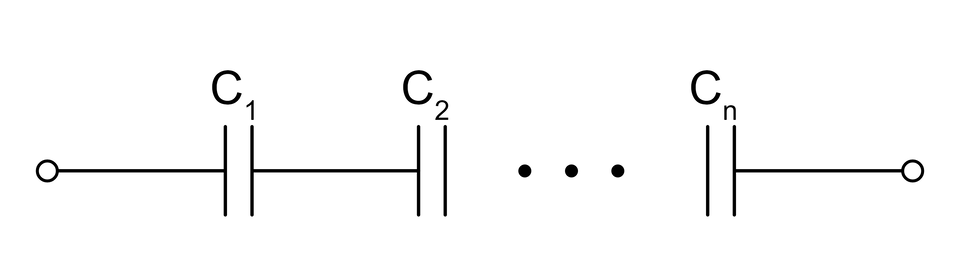
Połączenie szeregowe
Dla połączenia równoległego, możliwe jest przekształcenie połączonych ze sobą równolegle elementów, na odwrotność pojemności zastępczej wyrażoną wzorem:
Skutki działania prądu elektrycznego na organizm człowiek zależą od wielu czynników takich jak: wartość natężenia prądu przepływającego przez organizm, czas przepływu prądu a także droga porażenia.
Porażenie prądem elektrycznym może wywołać skutki o podłożu:
fizycznym – poparzenia, zerwanie mięśni, uszkodzenia kości,
chemicznym – zmiana stężenia jonów w organizmie,
biologicznym – uszkodzenia układu nerwowego, oddechowego i krążeniowego.
Napięcie bezpieczne jest to graniczna wartość napięć dla danego środowiska, przy którym wymuszony długotrwały przepływ prądu przez organizm człowieka, nie powinien stanowić zagrożenia dla zdrowa lub życia.
Ludzki organizm jest mniej wrażliwy na działanie prądu stałego względem porażenia prądem przemiennym, o czym może świadczyć znacznie większa wartość napięcia bezpiecznego.
Warunki środowiska | Napięcie stałe | Napięcie przemienne |
|---|---|---|
Normalne (suche) | ||
Szczególne (wilgotne) | ||
Ekstremalne (mokre) |
Prąd przemienny przepływając przez organizm, powoduje silne skurcze mięśni. Doprowadza to do sytuacji, w której osoba nie jest w stanie uwolnić się od elementu będącego źródłem porażenia, ze względu skurcz mięśni dłoni, uniemożliwiający jego puszczenie. Przyjmuje się iż maksymalna wartość natężenia prądu samouwolnienia, a więc sytuacji, w której porażony jest w stanie oderwać dłoń od elementu rażącego, zawiera się w przedziale dla prądu przemiennego o częstotliwości .
Istotnym warunkiem na skutki spowodowane porażenie prądem elektrycznym, jest droga jego przypływu. Najbardziej niebezpieczna jest droga ręka–ręka oraz ręka–noga. Wynika to z faktu iż znaczna część prądu przepływa przez serce zwiększając tym samym ryzyko wywołania migotania komór serca. Niebezpieczeństwo wystąpienia tego zaburzenia jest najwyższe w przypadku porażenia prądem przemiennym o częstotliwości , a więc wartościach występujących powszechnie w sieciach elektroenergetycznych oraz instalacjach elektrycznych.
Czwórnik jest to układ czterozaciskowy, posiadający dwie pary zacisków, spełniających warunek:
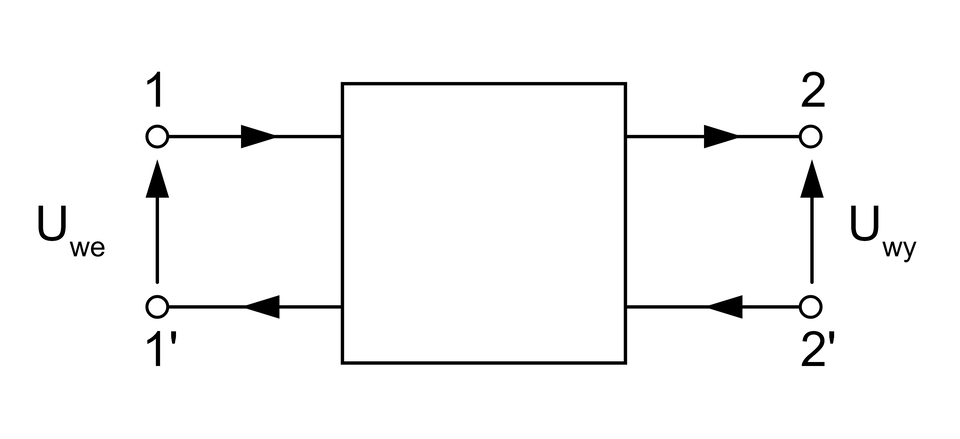
Czwórnik może zostać przestawiony jako układ czterozaciskowy z przedstawioną szczegółową budową układu, jak i w postaci schematu blokowego, którego struktura wewnętrzna nie jest znana.
Reprezentacja układu w postaci blokowej czwórnika wykorzystywana jest w przypadku schematów blokowych, które mają za zadanie przestawić ogólną budowę i sposób działania pewnego układu, bez wykorzystania szczegółowej reprezentacji graficznej układu w postaci schematów ideowych.
Szczegółowa reprezentacja czwórnika, przedstawiona jest w postaci schematu ideowego, który dokładnie opisuje budowę obwodu, przedstawiając całą jego strukturę.
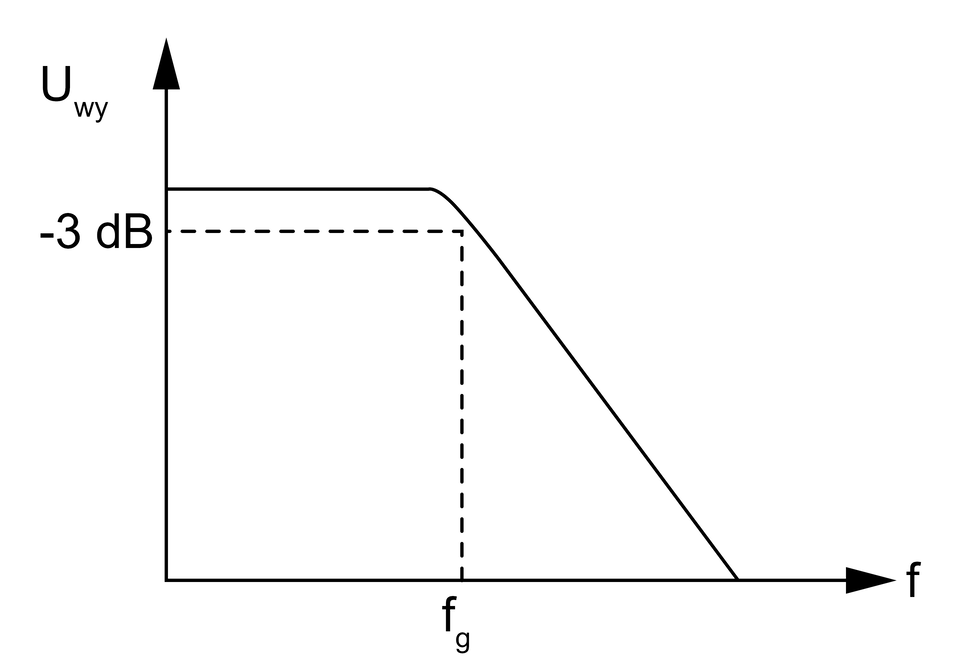
Filtr częstotliwościowy jest to układ w postaci czwórnika, przepuszczający sygnał z niewielkim tłumieniem (filtr rzeczywisty) o określonym paśmie częstotliwości oraz tłumiący sygnał o częstotliwości znajdującym się poza tym pasmem.
Pasmo częstotliwości, który jest przepuszczane przez filtr nazywane jest pasmem przepustowym. Częstotliwości znajdujące się w zakresie tłumienia filtra, nazywane jest pasmem tłumieniowym.
Częstotliwość sygnału znajdująca się na granicy pasma tłumieniowego oraz przepustowego, nazywana jest częstotliwością graniczną. Wartość ta odpowiada częstotliwości, przy której tłumienie sygnału przez filtr jest większe niż .
W zależności od zakresu częstotliwości przepuszczanych przez filtr, możemy podzielić je na cztery podstawowe rodzaje:
dolnoprzepustowe,
górnoprzepustowe,
pasmowe (środkowoprzepustowy),
pasmowozaporowe (środkowozaporowe).
Ze względu na swoją konstrukcję, filtry możemy podzielić na:
filtr jednostopniowy,
filtr wielostopniowy.
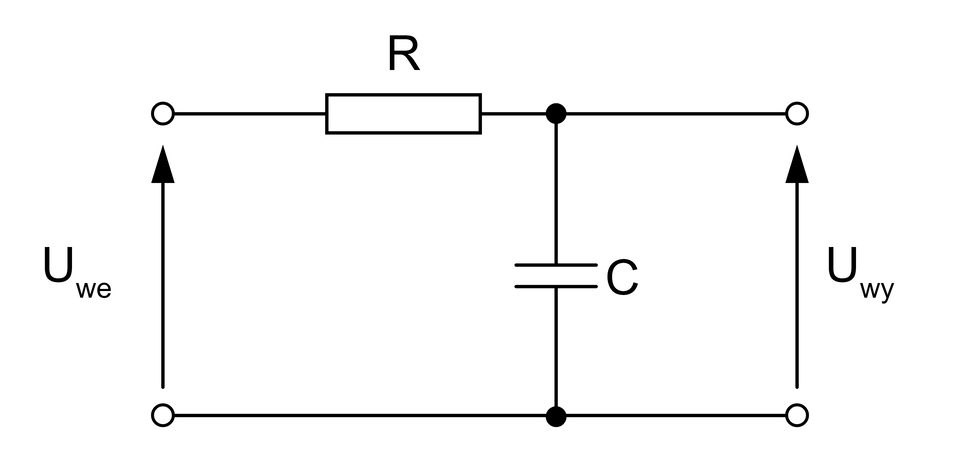
Filtr dolnoprzepustowy:
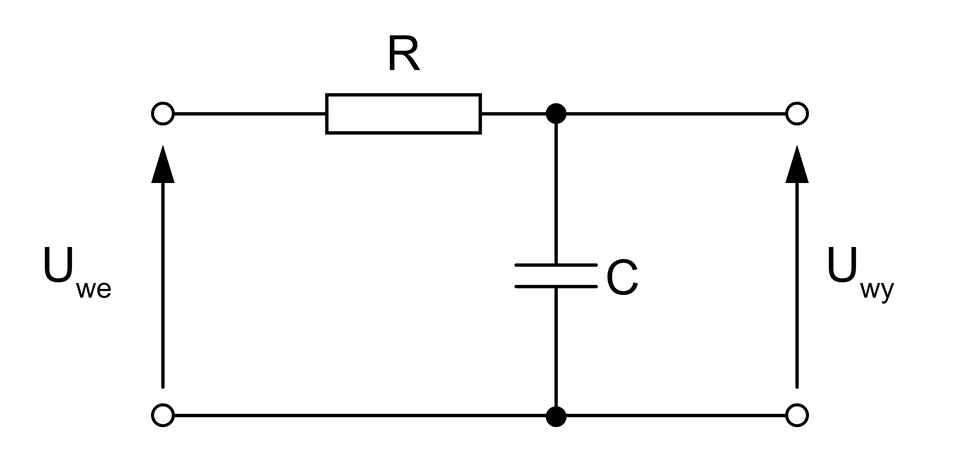
Filtr ten przenosi sygnał, którego częstotliwość zawiera się w przedziale od do . Częstotliwość graniczna filtra dolnoprzepustowego jest wyrażona wzorem:
gdzie:
to wartość rezystancji ,
to wartość pojemności .
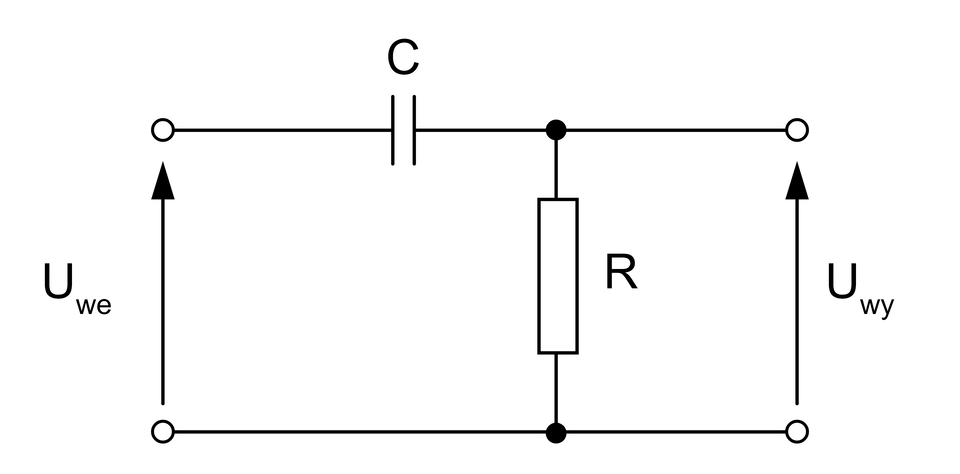
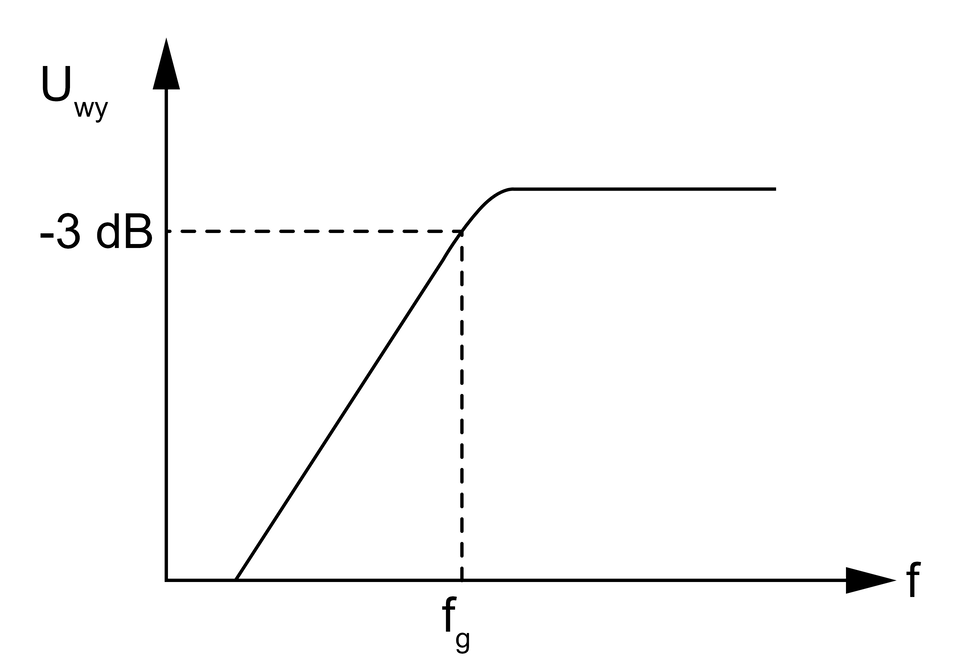
Filtr górnoprzepustowy:
Filtr ten przenosi sygnał, którego częstotliwość przyjmuje wartości .
Częstotliwość graniczna filtra górnoprzepustowego jest wyrażona wzorem:
gdzie:
to wartość rezystancji ,
– Wartość pojemności .
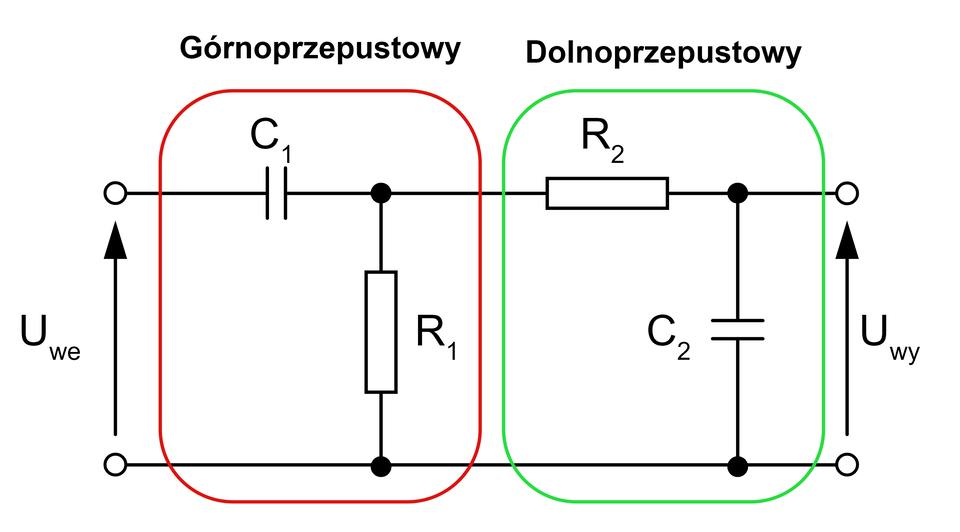
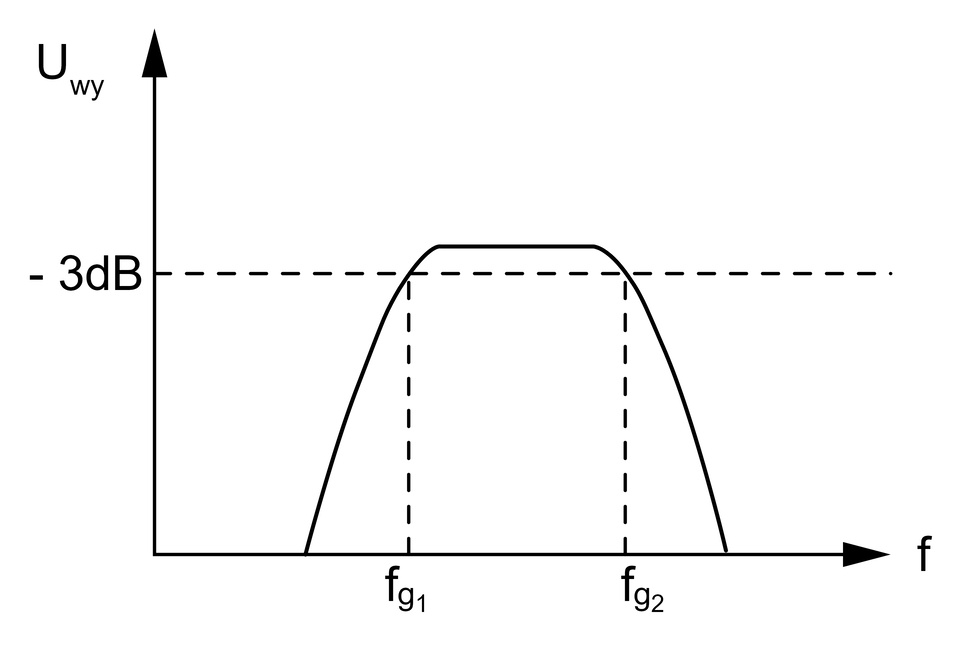
Filtr pasmowy (środkowoprzepustowy)
Filtr ten przenosi sygnał, którego częstotliwość przyjmuje wartości od do .
Powyższy schemat przedstawia filtr środkowoprzepustowy, który zbudowany jest z połączonego ze sobą filtra górnoprzepustowego oraz dolnoprzepustowego. Jest to więc konstrukcja wielostopniowa.
Częstotliwości graniczne filtra pasmowego są wyrażone wzorami:
gdzie:
, to wartość rezystancji ,
, to wartość pojemności .
Filtr środkowozaporowy (pasmowozaporowy)
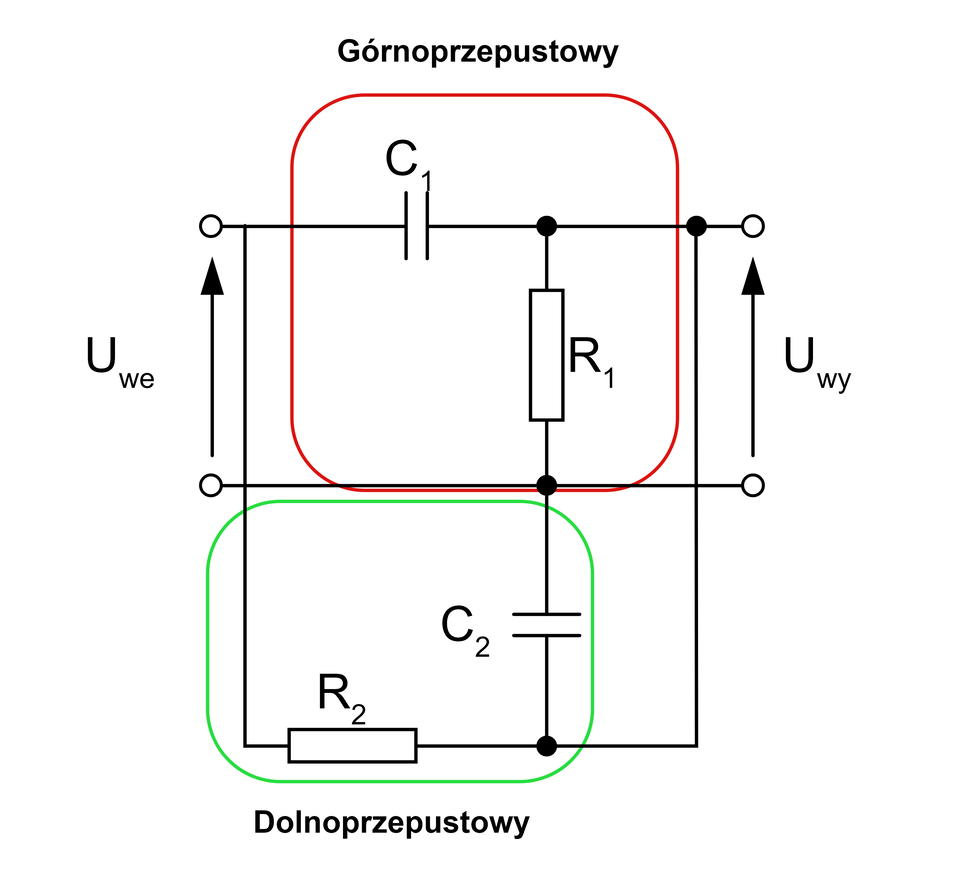
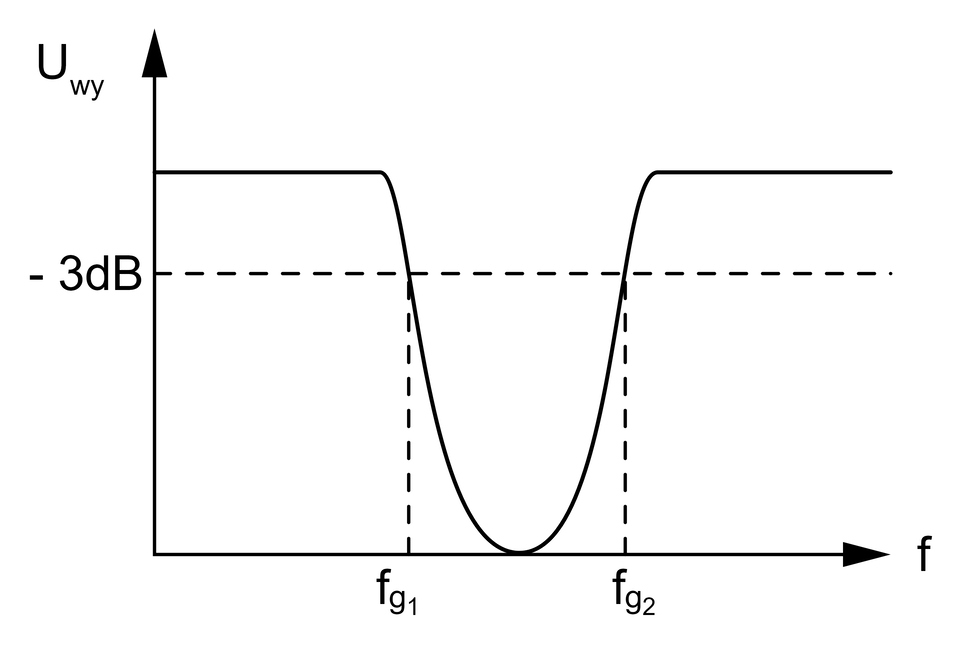
Filtr środkowozaporowy przenosi sygnał, którego częstotliwość przyjmuje wartości od do . Powyższy schemat przedstawia filtr środkowoprzepustowy, który zbudowany jest z połączonego ze sobą filtra górnoprzepustowego oraz dolnoprzepustowego.
Częstotliwości graniczne filtra środkowozaporowego są wyrażone wzorami:
gdzie:
, to wartość rezystancji ,
, to wartość pojemności .
Obwód zawierający przynajmniej jeden element nieliniowy, nazywamy obwodem nieliniowym. Jeżeli natomiast wszystkie elementy obwodu są elementami liniowymi, to obwód nazywamy liniowym.
Elementy, których charakterystyka prądowo–napięciowa jest wyrażona linią prostą, są nazywane elementami liniowymi. W elementach tych liniowe zmiany napięcia przyłożonego do zacisków, wywołują liniowe zmiany natężenia prądu, przepływającego przez element. Przykładem elementu liniowego jest rezystor.
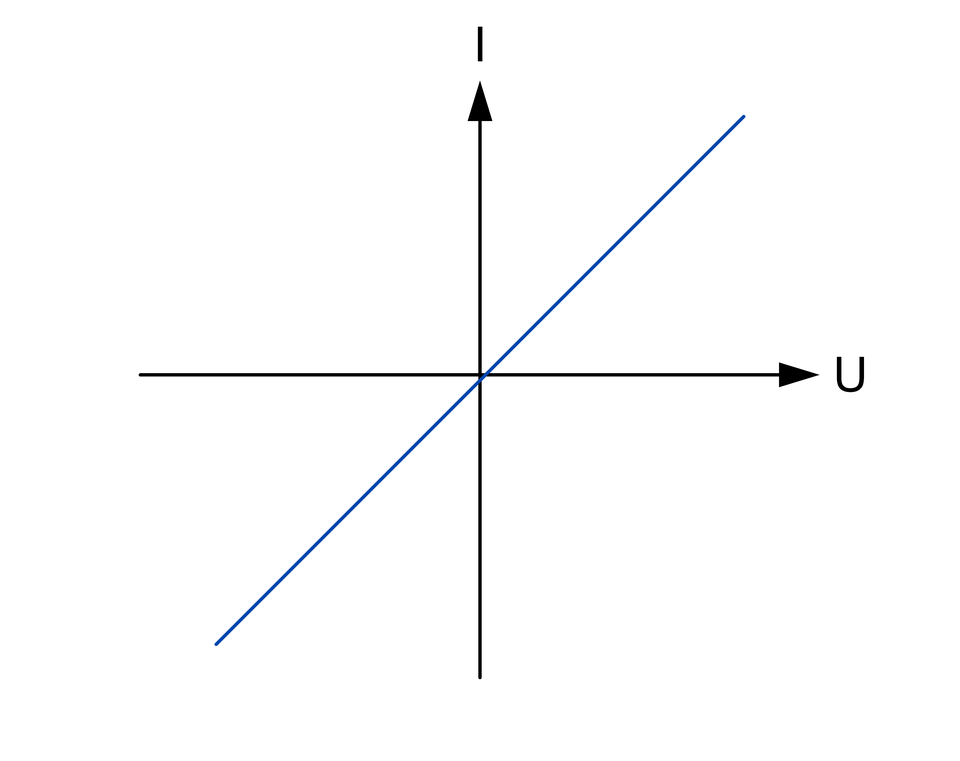
Elementy nieliniowe, posiadają nieliniowe charakterystyki prądowo–napięciowe. W przypadku tych elementów, liniowe zmiany napięcia przyłożonego do jego zacisków, wywołają nieliniowe zmiany natężenia prądu przepływającego przez element.
Przykładami elementów nieliniowych są: diody prostownicze, diody świecące,rezystory nastawne (regulowane), tranzystory itp.
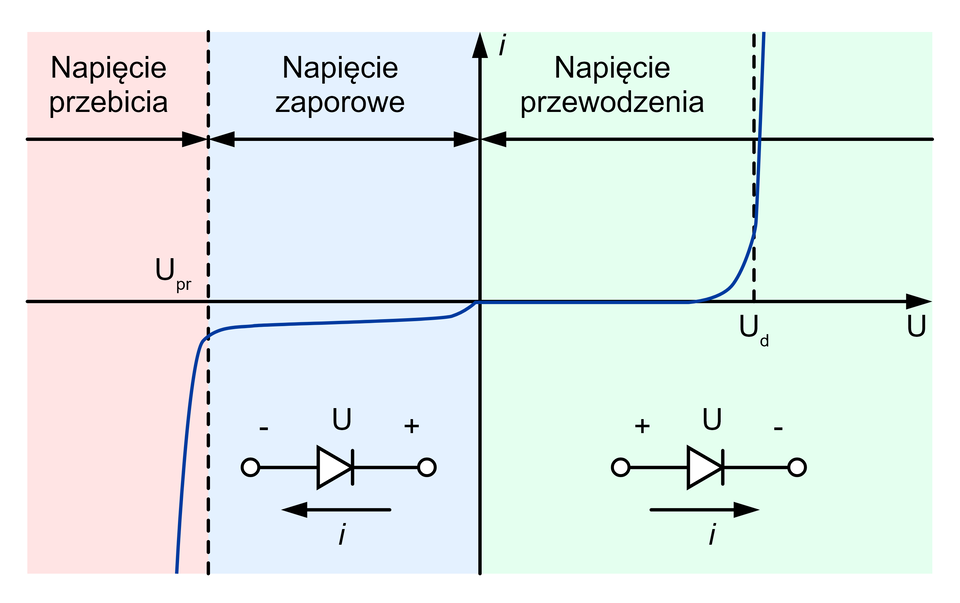
Na podstawie powyższej charakterystyki można zaobserwować nieliniowość diody prostowniczej oraz zauważyć pewną właściwość tego elementu. W momencie doprowadzenia napięcia w kierunku przewodzenia diody do poziomu nazywanego napięciem progowym , prąd przepływający przez element zaczyna gwałtownie wzrastać. Gdy dioda znajduje się w tym obszarze pracy, zaczyna ona przewodzić prąd elektryczny.
W przypadku gdy dioda jest spolaryzowana zaporowo, pod wpływem wzrostu napięcia, prąd jaki płynie przez element zmienia się w niewielkim zakresie. Natężenie prądu osiąga na tym odcinku charakterystyki niewielkie wartości. Po osiągnięciu wartości napięcia nazywanego napięciem przebicia , natężenie prądu zwiększa swoją wartość w sposób lawinowy. W zależności od osiągniętej wartości natężenia prądu oraz mocy jaka wydzieliła się na diodzie prostowniczej, może dojść do jej trwałego uszkodzenia. Jest to więc odcinek charakterystyki prądowo–napięciowej, w której wielkości te, podczas normalnej pracy diody nie powinny się znajdować.
Dioda prostownicza wykorzystuje wyżej opisane zjawisko do prostowania napięcia, a więc zamiany napięcia przemiennego na napięcie stałe (po odfiltrowaniu napięcia tętnień przez układy filtrujące).
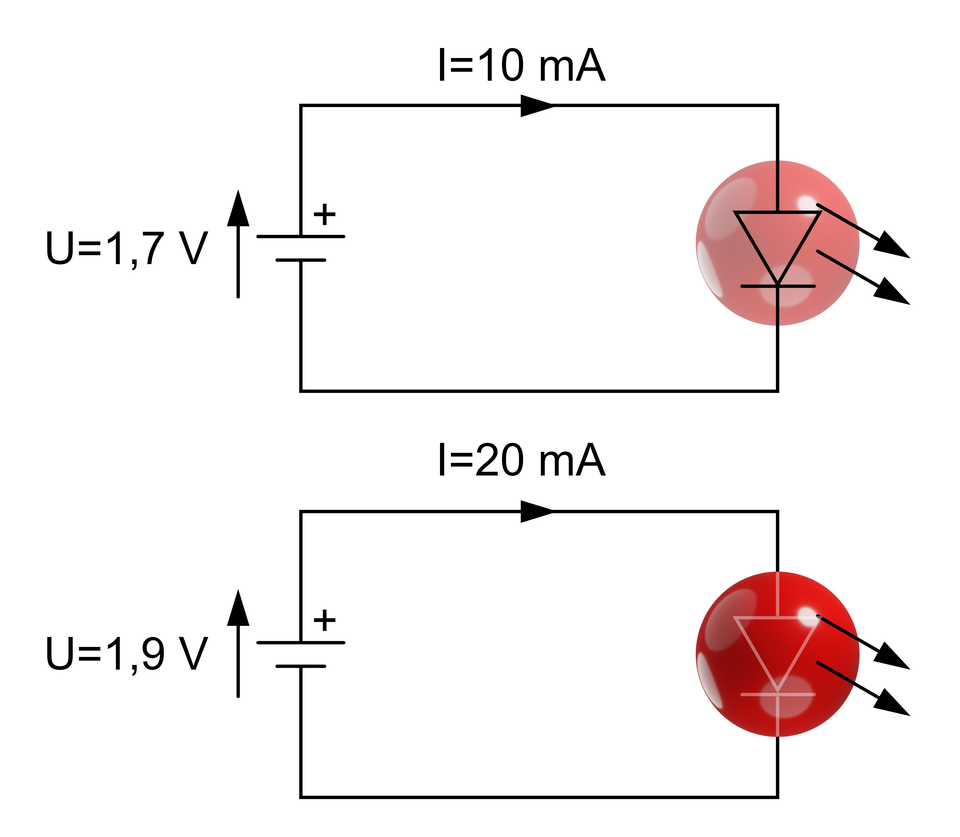
Innym przykładem elementu nieliniowego może być dioda świecąca (LED). Jej charakterystyka prądowo–napięciowa jest w zależności od swojej konstrukcji podobna do diody prostowniczej, z tą różnicą, że jej jedyny prawidłowy obszar charakterystyki pracy, znajduje się tylko w obszarze przewodzenia diody. Element ten nie może więc pełnić funkcji prostownika napięcia. Cechą charakterystyczną tego elementu, jest możliwość emitowania światła pod wpływem przyłożonego napięcia zasilającego. Zmieniając jego wartość możliwe jest regulowanie jego natężenia.
Wszystkie przebiegi napięcia lub prądów, których zmienność w funkcji czasu nie jest przebiegiem sinusoidalnym, nazywamy sygnałem odkształconym lub niesinusoidalnym.
Sygnały odkształcone może podzielić na:
okresowe,
nieokresowe.
Przykłady sygnałów odkształconych:
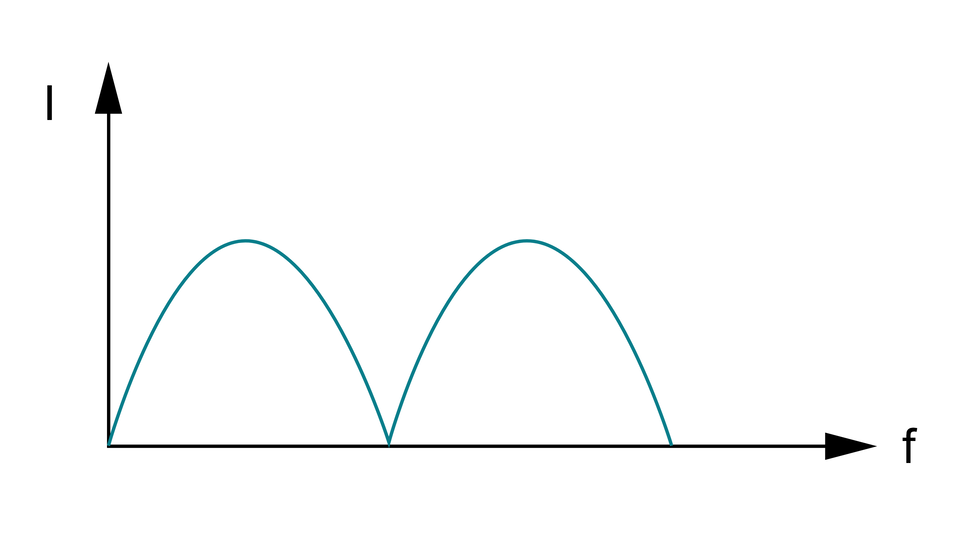
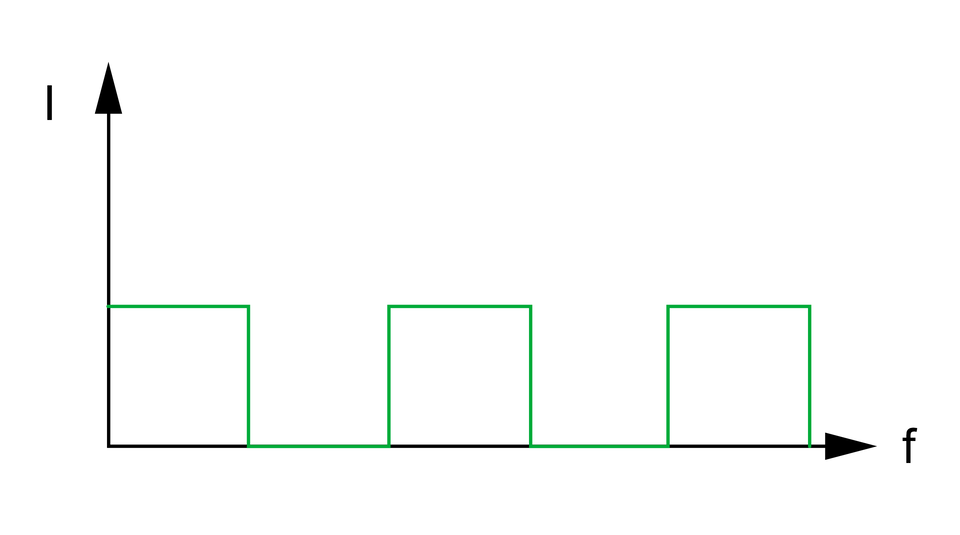
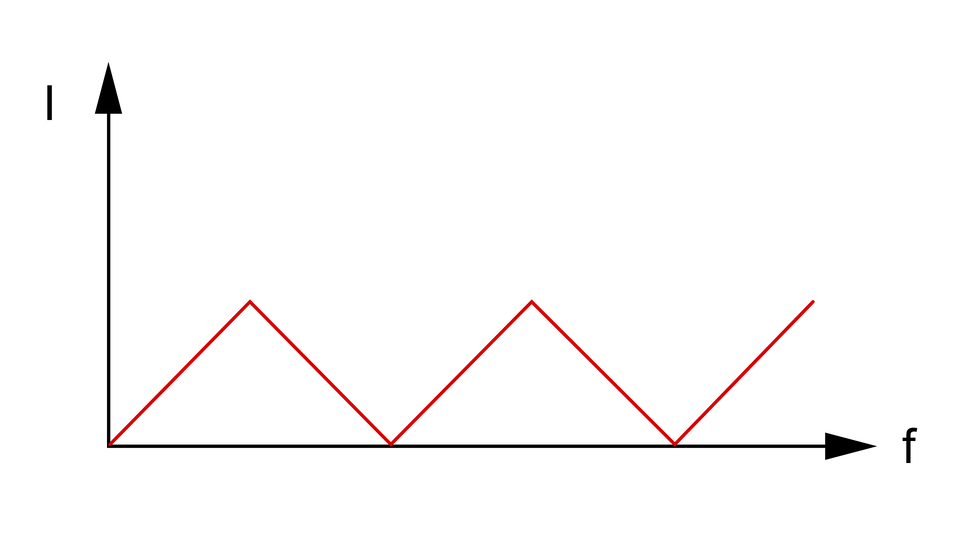
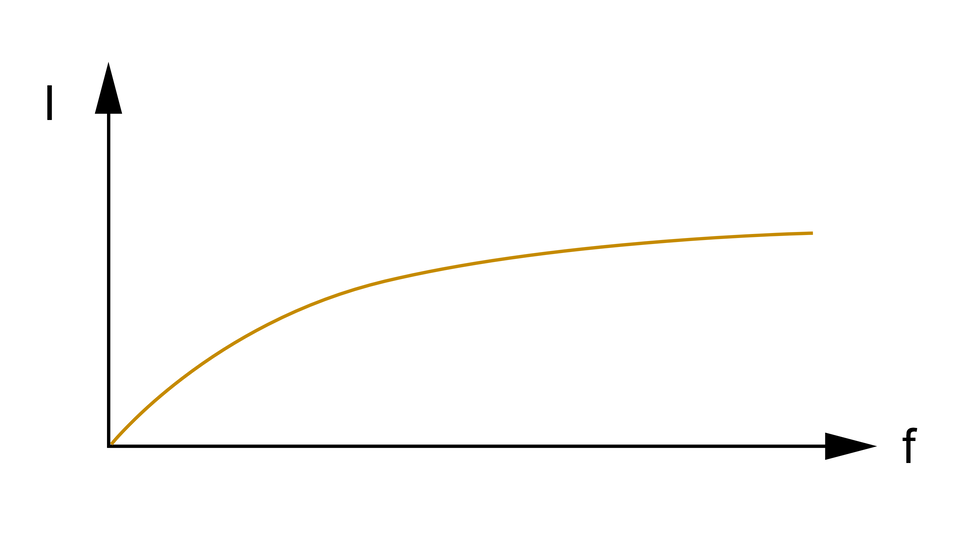
Stan ustalony charakteryzuje się tym iż przy wymuszeniu stałym podczas doprowadzenia prądu i napięcia o wartości stałej, odpowiedź układu na to wymuszenie również pozostaje stała i nie zmienia się w czasie. W rzeczywistych układach stan ustalony nigdy nie wystąpi ze względu na skończoną ilość energii jaką można dostarczyć do obwodu.
Rzeczywiste układy charakteryzują się występowaniem stanów nieustalonych. Powstaje on w momencie dołączenia źródła lub jakiejkolwiek zmiany struktury układu. Stan nieustalony charakteryzuje się tym iż w momencie jego wystąpienia, następuje zmiana wartości napięć i prądów aż do chwili w której wystąpi ustalenie się ich przebiegów (do wartości umownej). Okres w którym następuje początek stanu nieustalonego, do początku stanu ustalonego nazywamy komutacją. W wielu przypadkach czas trwania stanu nieustalonego jest wartością na tyle małą iż jest on pomijana, ze względu na niewielki wpływ na działanie układu. Jednakże w przypadku elementów zdolnych do gromadzenia energii takich jak cewki czy kondensatory, stan ustalony ma duże znaczenie na działanie układu i musi być on uwzględniony.
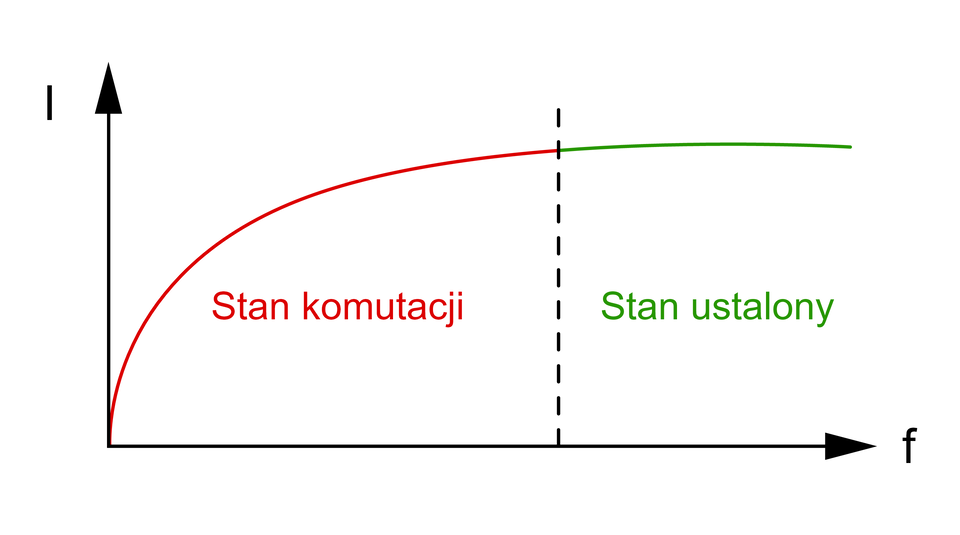
W celu łatwego określania przybliżonego czasu trwania czasu nieustalonego wprowadzono pojęcie stałej czasowej . Jest to czas, po którym nieustalona wartość napięcia osiągnęłaby wartość ustaloną, gdyby ten narastał w sposób liniowy. Jednostką stałej czasowej jest sekunda .
gdzie:
to rezystancja ,
to pojemność .
W praktyce przyjmuje się, iż stan ustalony następuje po upływie .
Układem trójfazowym nazywamy zespół obwodów elektrycznych, w których występują napięcia sinusoidalnie zmienne o jednakowej wartości częstotliwości oraz amplitudzie napięcia, przesunięte między sobą w fazie o wartość . Napięcia w układzie trójfazowym generowane są z jednego źródła energii elektrycznej, zwanym generatorem trójfazowym.
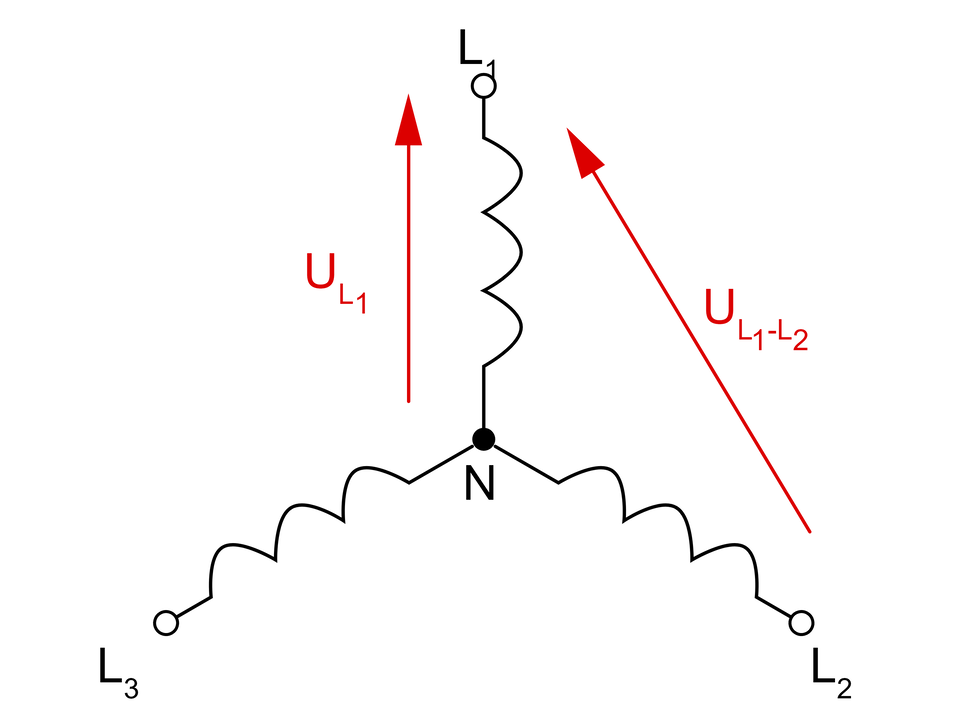
Poszczególne zaciski generatora trójfazowego (, , ) nazywane są fazami. Punkt środkowy, w którym zbiegają się wszystkie poszczególne fazy układu, nazywamy punktem neutralnym. Wartość napięcia występującego w tym punkcie przedstawia wzór:
Napięcie fazowe jest to napięcie występujące pomiędzy zaciskiem poszczególnej fazy układu a punktem neutralnym (, , ).
Napięciem międzyfazowym nazywamy napięcie występujący pomiędzy dwoma zaciskami poszczególnych faz układu (, , ).
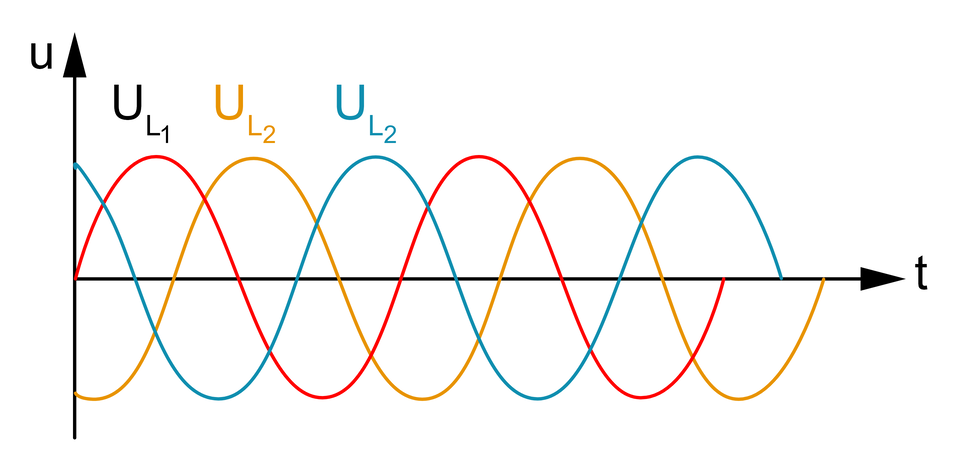
W układach trójfazowych elementy źródłowe lub odbiornikowe mogą zostać połączone w trójkąt lub gwiazdę.
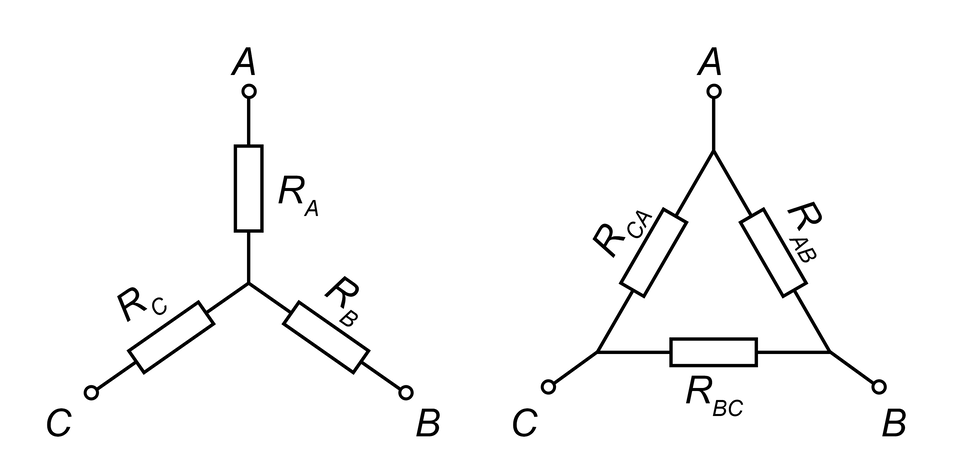
Przy zapewnieniu warunków niezmienności wartości napięć i prądów wstępujących w danych układach, możliwe jest wzajemne przekształcenie połączeń tj. zamiana połączenia elementów w trójkąt na połączenie typu gwiazda i na odwrót.
Zamiana układu połączenia elementów na układ równoważny nazywamy transfiguracją i jest ona wyrażona wzorami:
Przekształcenie trójkąt → gwiazda
Przekształcenie gwiazda → trójkąt
Układy trójfazowe są powszechnie stosowane przy przesyłaniu energii elektrycznej z wykorzystaniem trójfazowej sieci energetycznej. Zastosowanie tego rozwiązania jest zasadne ze względów ekonomicznych oraz technicznych.
Równie powszechnym wykorzystaniem układów trójfazowych jest stosowanie trójfazowych generatorów oraz silników, które ze względu na swoja prostą budowę oraz niezawodność, wykorzystywane są w pojazdach elektrycznych takich jak: pociągi, tramwaje, samochody elektryczne itp.
W wyniku przepływu prądu, w czasie t przez przekrój poprzeczny przewodnika następuje przemieszczenie ładunku wyrażony wzorem:
gdzie:
to wartość natężenia prądu ,
to czas przepływu prądu .
Energia jaka jest niezbędna do transportu tego ładunku wynosi:
gdzie:
to energia ,
to wartość napięcia ,
to wartość natężenia prądu .
Jednostką energii jest dżul , zgodnie z równaniem:
Moc elektryczna jest to stosunek energii prądu elektrycznego do czasu , która jest wyrażona wzorem:
Jednostką mocy jest wat .
Wartość skuteczna prądu sinusoidalnie przemiennego jest to wartość natężenia prądu stałego, którego przepływ przez przewodnik o określonej rezystancji, w czasie równym okresowi prądu sinusoidalnie przemiennego, spowoduje wydzielenie się na tym przewodniku takiej samej ilości energii cieplnej, jak w przypadku przepływy prądu sinusoidalnego w tym samym czasie. Wartość tą opisuje zależność:
gdzie:
to amplituda prądu sinusoidalnie przemiennego .
Wartość skuteczną napięcia sinusoidalnie przemiennego jest wyznaczona wzorem:
gdzie:
to amplituda napięcia sinusoidalnie przemiennego .
Moc czynna jest to iloczyn wartości skutecznej prądu i napięcia, oraz wartości ich kąta przesunięcia fazowego. Jednostką mocy czynnej jest wat .
gdzie:
to wartość napięcia ,
to wartość natężenia prądu ,
to kąt przesunięcia fazy początkowej przebiegów napięcia i prądu.
Przesunięcie fazowe przebiegów posiadających tą samą częstotliwość, nazywamy różnicę w ich fazie początkowej. W przypadku idealnych elementów o charakterze czysto rezystancyjnym, przesunięcie fazowe pomiędzy przebiegami prądu i napięcia nie występuje. Wartość dla tego typu elementów wynosi . W przypadku elementów idealnych o charakterze pojemnościowym przebieg napięcia jest opóźniony względem przebiegu prądu o kąt wynoszący . Dla elementów o charakterze indukcyjnym przebieg napięcia wyprzedza przebieg prądu o kąt .
Moc bierna jest to iloczyn wartości skutecznej prądu i napięcia oraz wartości ich kąta przesunięcia fazowego. Jednostką mocy czynnej jest war .
,
gdzie:
to wartość napięcia ,
to wartość natężenia prądu ,
to kąt przesunięcia fazy początkowej przebiegów napięcia i prądu.
Moc pozorna jest to wielkość, która wiąże moc czynną oraz moc bierną, poprzez opisanie jej wyrażeniem:
gdzie:
to wartość mocy czynnej ,
to wartość mocy biernej .
Jednostką mocy pozornej jest woltoamper .
Współczynnik mocy jest to iloraz mocy czynnej i mocy pozornej, który można zapisać w postaci:
Moc bierna wyraża określoną ilość energii pobieranej ze źródła, która nie jest przetwarzana na użyteczną pracę czy ciepło. Stwarza to istotny problem przy wytwarzaniu i przesyłaniu energii elektrycznej, gdyż występowanie mocy biernej, powoduje zwiększenie moc strat przesyłowych linii elektroenergetycznych, a także wymusza budowę generatorów o większej mocy znamionowej.
W celu zmniejszenia udziału mocy biernej występującej w urządzeniach, dąży się do zbliżenia wartości współczynnika mocy danego urządzenia do jedności. Realizuje się to poprzez stosowanie kompensacji mocy biernej. Jedną z najbardziej powszechnych metod kompensacji jest stosowanie kondensatorów lub ich zespołów, przy urządzeniach o charakterze indukcyjnym np. silniki elektryczne.
Pole magnetyczne jest to stan w przestrzeni charakteryzujący się tym, iż siła działa w tym polu wyłącznie na ruchome ładunki elektryczne.
Cechą charakteryzującą pola magnetyczne jest zmiana właściwości niektórych materiałów pod wpływem jego działania oraz to iż w przewodniku znajdującym się w tym polu indukuje się napięcie elektryczne.
Na przewodnik o długości , w którym występuje przepływ prądu elektrycznego, znajdujący się w polu magnetycznym, działa siła wyrażona wzorem:
gdzie:
to indukcja magnetyczna ,
to wartość natężenia prądu ,
to długość przewodu przecinająca linie pola magnetycznego .
Wzór można przekształcić do postaci:
Powyższy wzór umożliwia wyznaczenie indukcji magnetycznej, a więc podstawowej wielkości opisującej pole magnetyczne. Jednostką indukcji magnetycznej jest tesla .
Strumień magnetyczny jest definiowany jako iloczyn indukcji magnetycznej oraz pola powierzchni . Dla powierzchni płaskiej , która znajduje się prostopadle do kierunku linii pola magnetycznego, strumień magnetyczny można opisać wzorem:
gdzie:
to strumień indukcji magnetycznej ,
to indukcja magnetyczna ,
to pole powierzchni obiektu znajdującego się w polu magnetycznym .
Jednostką strumienia magnetycznego jest Weber .
Przenikalność magnetyczna opisuje właściwości magnetyczne środowiska. Jest ona wyrażona wzorem:
gdzie:
to stała magnetyczna wynosząca .
W powyższym wzorze opisana jest przenikalność magnetyczna względna , która określa w jakim stopniu przenikalność magnetyczna danego środowiska jest większa od przenikalności magnetycznej próżni. Wielkość ta jest wielkością niemianowaną.
Natężenie pola magnetycznego , jest to wielkość wektorowa, umożliwiająca określenie pola magnetycznego, która nie zależy od właściwości magnetycznych środowiska. Wektor natężenia pola magnetycznego można opisać wzorem:
W postaci skalarnej można przedstawić relację pomiędzy indukcją a natężeniem pola magnetycznego poprzez opisanie go wzorem:
Jednostką natężenia pola magnetycznego jest amper na metr .
Natężenie pola magnetycznego w osi rdzenia cewki można wyznaczyć stosując wzór:
gdzie:
– natężenie prądu płynącego przez uzwojenia cewki ,
– ilość zwojów cewki,
– długość cewki .
Cewka o długości oraz powierzchni przekroju poprzecznego wynoszącej , ma nawinięte uzwojenie o liczbie zwojów równej . Przez uzwojenie cewki przepływa prąd o wartości . Indukcja ferrytowego rdzenia cewki wynosi . Posiadając powyższe dane oblicz wartość strumienia magnetycznego oraz natężenie pola magnetycznego w rdzeniu.
Etap 1: Obliczanie wartości strumienia magnetycznego w rdzeniu ferrytowym.
Przekształcamy jednostkę pola powierzchni przekroju poprzecznego cewki:
.
Podstawienie danych do wzoru na strumień magnetyczny:
.
Etap 2: Obliczanie wartości natężenia pola magnetycznego w rdzeniu.
Podstawienie danych do wzoru na natężenie pola magnetycznego.
.