Rk0W7LPVJR8oy1

Zdjęcie przedstawia w zbliżeniu silnik samolotu dwupłatowego i centralną część śmigła. Śmigło żółte, drewniane, silnik w konstrukcji gwiazdowej, z czarnymi cylindrami rozmieszczonymi koncentrycznie wokół centralnego wału korbowego w srebrnej oprawie. Na cylindrach wyraźne ożebrowanie służące lepszemu odprowadzaniu ciepła. Z tyłu część kadłuba samolotu w kolorze zielonym oraz fragment górnego skrzydła w kolorze żółtym. W lewym dolnym narożniku kadru w tle trawa i drzewa.

1. Praca

RDEadFzvvlbC81

Fiz_gim_kl2_d5_m17_rysunek _1_Syzyf

1. Znaczenie słowa praca w języku potocznym nie pokrywa się z jego znaczeniem w języku fizyki.

2. W języku fizyki praca $W$ to zdefiniowana wielkość, będąca iloczynem siły $F$ i przemieszczenia $s$, jeśli kierunki siły i przemieszczenia są takie same; w takiej sytuacji możemy ją wyrazić wzorem:
   $W=F·s$

3. Jednostką pracy jest dżul, oznaczamy ją literą $\mathrm{J}$.
   $\mathrm{1 dżul}=\mathrm{1 niuton}·\mathrm{1 metr}$, co oznacza, że 1 J jest równy pracy wykonanej przez siłę 1 N na drodze 1 m.
   $\mathrm{1\; J}=\mathrm{1\; N}·\mathrm{1\; m}$

4. Praca siły prostopadłej do przemieszczenia ma wartość zero.

2. Moc

R1QcBStpy1TBd1

Fiz_gim_kl2_d5_m17_zdjęcie_1_silnik

1. Moc informuje nas, jaka jest szybkość wykonywanej pracy lub inaczej – ile pracy wykonywano w jednostce czasu.

2. Moc $P$ jest równa ilorazowi pracy $W$ i czasu $t$, w którym ta praca została wykonana: $P= \frac{W}{t}$. Jeżeli praca była wykonywana ze zmienną szybkością, to otrzymamy wartość średniej mocy.

3. Jednostką mocy w układzie SI jest wat. Urządzenie ma moc 1 wata, jeśli w ciągu 1 sekundy wykonuje pracę 1 dżula: $1=\frac{1\mathrm{ J}}{1\mathrm{ s}}$.

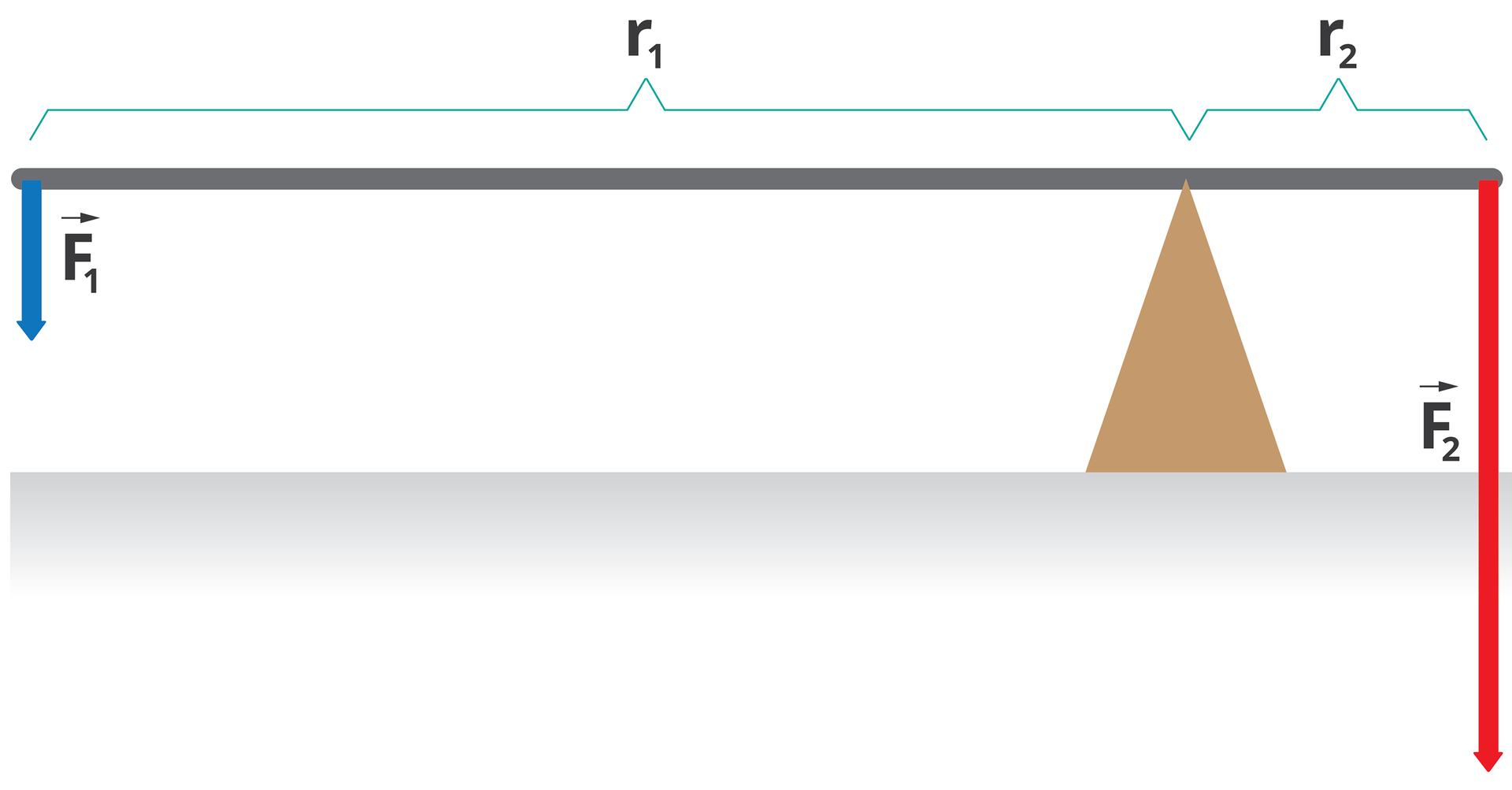
3. Maszyny proste

RVmMwfYUA9ifi1

Fiz_gim_kl2_d5_m17_rysunek_2_dzwignia

1. Maszyny proste to urządzenia ułatwiające wykonanie pracy. Należy podkreślić, że nie zmniejszają one wykonanej pracy, ale pozwalają wykonać pracę z użyciem mniejszej siły.

2. Przykładami maszyn prostych są:

   • dźwignia jednostronnaiyGRGMMBng_d858e131dźwignia jednostronna – sztywny pręt podparty w jednym punkcie, do którego siły są przyłożone po jednej stronie punktu podparcia;

   • dźwignia dwustronnaiyGRGMMBng_d858e137dźwignia dwustronna – sztywny pręt podparty w jednym punkcie, do którego siły są przyłożone po obu stronach punktu podparcia;

   • blok nieruchomy (rodzaj dźwigni dwustronnej) – to koło zamocowane na osi, przez które przerzucono linę. Ponieważ ramiona obu sił są takie same (ich wartość jest równa promieniowi koła), to również siły po obu stronach osi obrotu mają taką samą wartość. Użycie bloku nieruchomego pozwala zmienić kierunek siły działania;

   • kołowrótiyGRGMMBng_d858e150kołowrót – maszyna prosta będąca walcem o promieniu $r$ z umocowaną na jego końcu korbą o ramieniu $\mathrm{R }>\mathrm{ r}$. Osią obrotu kołowrotu jest jego oś symetrii. Na kołowrót jest nawinięta lina, której jeden koniec jest przymocowany do kołowrotu, a na drugi działa siła obciążająca $Q$. Wprawiająca w ruch siła $F$ działa prostopadle do ramienia korby i jest równa: $F= \frac{r}{R}·Q$.

iyGRGMMBng_d858e131

R10gW39MkAwXZ1

Dźwignia jednostronna

iyGRGMMBng_d858e137

RN0fcnyX0qGcA1

Zasada działania dźwigni dwustronnej

iyGRGMMBng_d858e150

R8i12FW68i2NT1

Kołowrót studzienny

4. Energia mechaniczna

R1Zxn2WJI00d11

Fiz_gim_kl2_d5_m17_rysunek_3_tryby

1. Energię posiada ciało lub układ ciał, które mają zdolność do wykonania pracy. Może ona występować w różnych formach, np. energia elektryczna, energia cieplna, energia chemiczna, energia mechaniczna.

2. Jednostką energii jest dżul.

3. Energia ciała może się zmieniać. Gdy ciało wykonuje pracę, jego energia maleje, a podczas gdy siły zewnętrzne wykonują pracę nad ciałem – jego energia wzrasta o wartość wykonanej pracy.

4. Energia mechaniczna jest sumą energii kinetycznej i potencjalnej.

5. Do oznaczenia energii najczęściej używa się symbolu $E$: $E_{\mathrm{mech}}= E_{\mathrm{kin}}+ E_{\mathrm{pot}}$

5. Energia potencjalna

R1KPzUqTZxark1

Fiz_gim_kl2_d5_m17_zdjęcie_2_wodospad

1. Energia potencjalna jest jedną z form energii mechanicznej. Posiadają ją ciała, które oddziałują ze sobą (przyciągają się lub odpychają), a jej wartość zależy od położenia tych ciał względem siebie. Jeśli między ciałami działa siła grawitacji – mówimy o energii potencjalnej grawitacji.

2. Energia potencjalna grawitacji to energia układu ciał oddziałujących siłami grawitacyjnymi. Wartość tej energii zależy od masy ciał oraz od odległości między nimi; rośnie, gdy zwiększa się odległość między oddziałującymi ciałami oraz jest większa w przypadku ciał o większej masie.

3. Wartość grawitacyjnej energii potencjalnej dla ciała o masie $m$ znajdującego się w pobliżu powierzchni Ziemi obliczamy ze wzoru:
   $E_{\mathrm{pot}}=m·g·h$,
   gdzie $h$ oznacza wysokość ponad pewien umownie przyjęty poziom (gdy energia potencjalna ciała jest równa zero).
   Oznacza to, że wartość energii potencjalnej grawitacji zależy od wyboru poziomu, względem którego ją obliczamy. Ponieważ oddziaływanie Ziemi słabnie ze wzrostem odległości od niej, zależność ta jest prawdziwa blisko powierzchni Ziemi.

4. Przyrost energii potencjalnej grawitacji nie zależy od wyboru poziomu odniesienia i jest wprost proporcjonalny do masy ciała i zmiany wysokości.

5. Energia potencjalna sprężystości to energia zgromadzona w ciałach odkształconych sprężyście. Odkształconych to znaczy rozciągniętych, ściśniętych, wygiętych lub skręconych. Wartość tej energii jest wprost proporcjonalna do kwadratu odkształcenia oraz zależy od właściwości sprężystych odkształcanego ciała. Zawsze jest równa pracy, jaką trzeba włożyć, aby odkształcić ciało.

6. Energia kinetyczna

RtaErG9vZBSNj1

Zdjęcie pocisku w ruchu – wyraźne widoczny ruch.

1. Energia kinetyczna to jedna z form energii mechanicznej. Posiadają ją ciała będące w ruchu i zależy ona od masy ciała oraz wartości jego prędkości.

2. Energia kinetyczna ciała równa jest pracy, jaką trzeba wykonać, aby ciało o masie m rozpędzić do prędkości v (lub zatrzymać ciało będące w ruchu).

3. Wartość energii kinetycznej ciała równa jest iloczynowi połowy masy ciała i kwadratu wartości prędkości ciała:
   $\mathrm{energia kinetyczna}= \frac{1}{2}·\mathrm{masa}·{\left(\mathrm{prędkość}\right)}^2$ 
   $E_{\mathrm{kin}}=\frac{1}{2}·m·v^2$

4. Energia kinetyczna ciała jest wprost proporcjonalna do masy ciała; to znaczy, że na przykład trzykrotne zwiększenie masy ciała powoduje trzykrotny wzrost jego energii kinetycznej (przy niezmienionej prędkości).

5. Energia kinetyczna ciała jest proporcjonalna do kwadratu prędkości, co oznacza, że na przykład trzykrotny wzrost prędkości powoduje aż dziewięciokrotny wzrost jego energii kinetycznej (przy stałej masie ciała).

6. Wartość energii kinetycznej zależy od układu odniesienia, ponieważ prędkość ciała zależy od układu odniesienia.

7. Ciała o różnych masach mogą mieć takie same energie kinetyczne, jeśli mają różne prędkości. Ciało o masie np. 100 razy mniejszej osiągnie taką samą energię kinetyczną jak ciało masywniejsze, jeśli jego prędkość będzie 10 razy większa.

7. Zasada zachowania energii

R1W3YM6tLF3i11

Fiz_gim_kl2_d5_m17_rysunek_4 _E_const

1. Zasada zachowania energii mechanicznej ma charakter empiryczny, to znaczy, że została sformułowana jako wniosek z bardzo wielu doświadczeń.

2. Zasada zachowania energii mechanicznej głosi, że jeżeli siły zewnętrzne nie wykonują pracy nad układem ciał i na składniki układu nie działają siły tarcia lub oporu ośrodka, to energia mechaniczna układu pozostaje stała. To znaczy, że energie kinetyczna i potencjalna składników układu mogą się zmieniać, ale ich suma pozostaje niezmieniona. Można to zapisać równaniem: ${(E_{\mathrm{pot}}+E_{\mathrm{kin}})}_{\mathrm{pocz}}={(E_{\mathrm{pot}}+E_{\mathrm{kin}})}_{\mathrm{kon}}$

3. Zasada zachowania energii mechanicznej ma duże znaczenie praktyczne, ponieważ pozwala w łatwy i prosty sposób obliczyć lub przynajmniej oszacować niektóre wielkości opisujące stan układu ciał w różnych procesach.

8. Temperatura a energia kinetyczna cząsteczek

RkCCHdPJ62bGQ1

Fiz_gim_kl2_d5_m17_rysunek_5_termometr

1. Temperatura jest wielkością opisującą stan cieplny ciała i jest miarą stopnia jego nagrzania. Mierzymy ją w stopniach Celsjusza lub kelwinach.

2. Temperatura związana jest ze średnią energią kinetyczną atomów i cząsteczek – dwa ciała mają taką samą temperaturę, jeśli średnia energia kinetyczna ich atomów lub cząsteczek jest taka sama.

3. Temperatura to nie to samo co ciepło, które jest jedną z form przekazywania energii.

4. W skali Kelvina (zwanej też bezwzględną skalą temperatur) temperatura jest wprost proporcjonalna do średniej energii kinetycznej atomów lub cząsteczek.

5. Zero kelwinów (zero bezwzględne temperatur) to najniższa wartość temperatury, w której ustaje ruch termiczny atomów i cząsteczek; ich energia kinetyczna byłaby wówczas równa zeru.

6. Temperaturę odczytaną w stopniach Celsjusza przeliczamy na kelwiny, dodając liczbę 273: $T_{\mathrm{Kelvina}}=T_{\mathrm{Celsjusza}}+273$

7. Różnica temperatur ma taką samą wartość zarówno w skali Celsjusza, jak i w skali bezwzględnej.

9. Energia wewnętrzna i I zasada termodynamiki

R17xnpw1NCrR81

Fiz_gim_kl2_d5_m17_rysunek_6_pierwsza_z_t

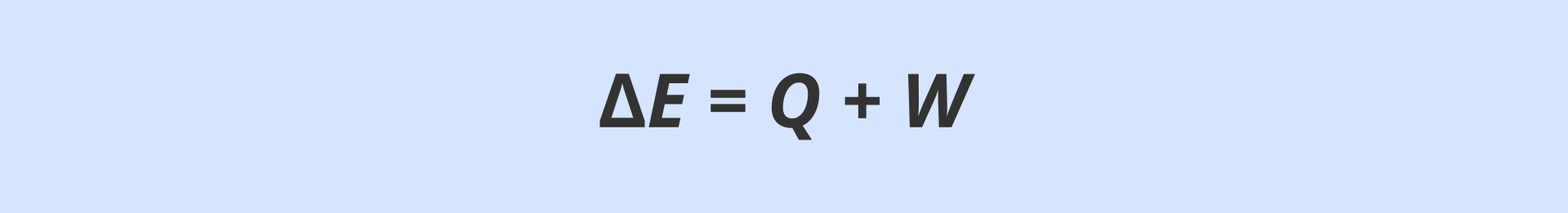
1. Praca sił tarcia zamienia energię kinetyczną ciała na jego energię wewnętrzną.

2. Energia wewnętrzna ciała to suma energii kinetycznych i potencjalnych wszystkich atomów i cząsteczek tworzących to ciało.

3. Wartość energii wewnętrznej zależy od:

   • liczby atomów i cząsteczek tworzących ciało – więcej cząsteczek to więcej składników sumy;

   • temperatury ciała – wyższa temperatura to większa wartość średniej energii kinetycznej cząsteczek;

   • rodzaju substancji i stanu jej skupienia – wielkość energii potencjalnej pochodzącej od oddziaływań międzycząsteczkowych zmienia się wraz ze stanem skupienia i jest różna dla różnych substancji.

4. Pierwsza zasada termodynamiki głosi, że zmiany energii wewnętrznej ciała wywoływane są pracą oraz przepływem energii cieplnej. Całkowita zmiana energii wewnętrznej jest sumą zmian wywołanych pracą i wymianą ciepła z otoczeniem: $∆E_{\mathrm{wew}}=W+Q$ 
   gdzie:
   $∆E_{\mathrm{wew}}$ – zmiana energii wewnętrznej;
   $W$ – praca;
   $Q$ – ciepło.

10. Przewodnictwo cieplne

RN3EefwUsE82F1

Zdjęcie paczki styropianu z napisem: λ = 0,046 W/m2

1. Przewodnictwo cieplne polega na przekazywaniu energii pomiędzy częściami ciała, których temperatury są różne. Ze zjawiskiem tym mamy do czynienia, gdy wydzieloną część ciała podgrzejemy. Po pewnym czasie, dzięki przekazywaniu energii, temperatura ciała wyrówna się.

2. Wielkością przenoszoną w procesie przewodnictwa jest ciepło, a zjawisko zachodzi dzięki różnicy temperatur.

3. Mechanizm przewodnictwa cieplnego oparty jest na bezpośrednim przekazywaniu energii kinetycznej między cząsteczkami lub atomami materii.

4. Ze względu na zdolność transportowania energii wewnętrznej substancje dzielimy na:

   • przewodniki ciepła – energia wewnętrzna jest w nich transportowana szybko i łatwo;

   • izolatory cieplne – transport energii wewnętrznej zachodzi w nich wolno.

5. Najlepszymi przewodnikami ciepła są: metale (również ciekłe), grafit, diament.

6. Dobrymi izolatorami ciepła są: gazy, pierze, wata szklana, korek, styropian, futro.

11. Konwekcja

Ri763IFhWYN291

Fiz_gim_kl2_d5_m17_rysunek_7_konwekcja

1. Konwekcja to proces przekazywania energii wewnętrznej przenoszonej przez poruszające się gaz lub ciecz.

2. Konwekcja swobodna – przyczyną ruchu gazu lub cieczy są różnice gęstości obszarów o różnej temperaturze.

12. Ciepło właściwe

RrPsQP1NtKGrC1

ćwiczenie 8

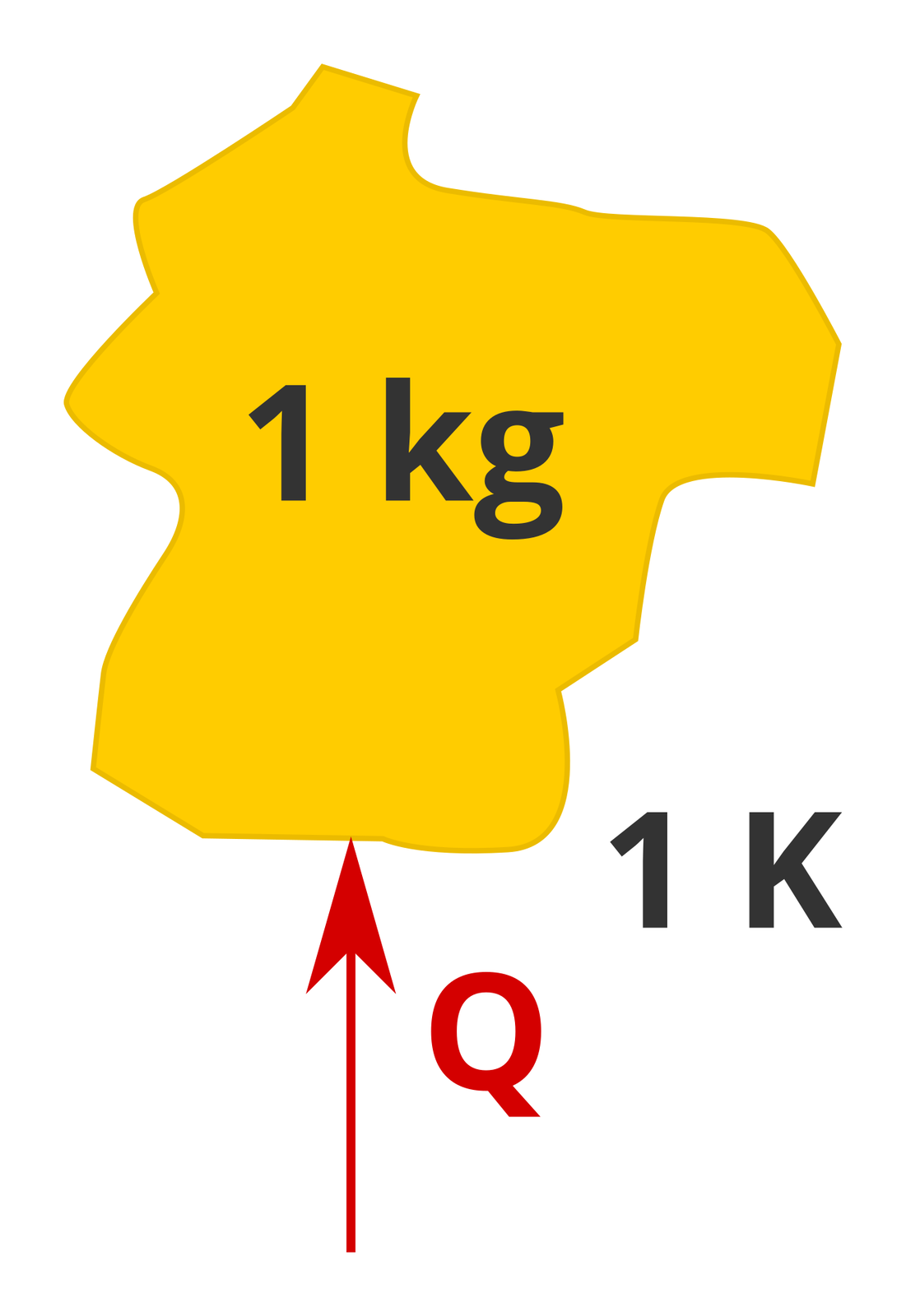
1. Ciepło właściwe to ilość energii potrzebna do ogrzania 1 kilograma substancji o jeden stopień Celsjusza (o jeden kelwin). Jest to wielkość charakteryzująca daną substancję. Jednostką ciepła właściwego w układzie SI jest $\left[\frac{\mathrm{J}}{\mathrm{kg}·\mathrm{K}}\right]$.

2. Definicję ciepła właściwego możemy zapisać za pomocą zależności: $c=\frac{Q}{m·∆T}$ ,
   gdzie:
   $c$ – ciepło właściwe;
   $m$ – masa ciała;
   $\mathrm{\Delta }T$ – przyrost temperatury;
   $Q$ – energia dostarczona do ciała w formie cieplnej (ciepło). Można ją obliczyć po przekształceniu powyższej zależności.

Otrzymamy wtedy: $Q=m·c·\mathrm{\Delta }T$

13. Wyznaczanie ciepła właściwego wody

RYxqfyWQlENgY1

Fiz_gim_kl2_d5_m17_rysunek_9_kalorymetr

Aby wyznaczyć ciepło właściwe wody, musimy wykonać następujące działania:

1. zmierzyć ilość energii dostarczonej do wybranej ilości wody;

2. zmierzyć masę wody;

3. zmierzyć zmianę temperatury, będącą skutkiem dostarczania energii do wody.

Ad 1. Do tego działania najwygodniej jest użyć źródła ciepła o znanej mocy $P$ (najlepiej czajnika lub grzałki elektrycznej) i zmierzyć czas jego pracy $\tau$. W urządzeniach tych cała energia elektryczna zamieniana jest na ciepło.
Ad 2. Masę wody możemy wyznaczyć, używając wagi lub mierząc jej objętość – w tym przypadku korzystamy ze znajomości gęstości wody.
Ad 3. Termometrem możemy zmierzyć temperaturę początkową wody, a ogrzewając wodę do momentu rozpoczęcia wrzenia, uznajemy, że temperatura końcowa wody osiągnęła wartość $100\mathrm{˚C}$. Nie mierzymy tej temperatury termometrem, głównie ze względów bezpieczeństwa.

14. Ciepło topnienia i krzepnięcia

R67drpSkfKnev1

Fiz_gim_kl2_d5_m17_rysunek_10_wosk

1. Aby stopić ciało stałe, należy dostarczyć mu energii, a aby zestalić ciecz – pobrać od niej energię.

2. Ciepło topnienia (krzepnięcia) to ilość energii, jaką należy dostarczyć (odebrać), aby stopić (zestalić) 1 kilogram danej substancji. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła topnienia w układzie SI jest $\left[\frac{\mathrm{J}}{\mathrm{kg}}\right]$.

3. Definicję ciepła topnienia możemy zapisać za pomocą zależności: $L=\frac{Q}{m}$,
   gdzie:
   $L$ – ciepło topnienia;
   $m$ – masa ciała;
   $Q$ – energia (ciepło) dostarczone do ciała.

15. Ciepło parowania i skraplania

R1aLgFmLxua3P1

Fiz_gim_kl2_d5_m17_rysunek_11_pranie

1. Parowanie cieczy oraz wrzenie (parowanie w całej objętości cieczy) wymaga dostarczania energii do cieczy, natomiast skraplanie wymaga odbierania energii od substancji w fazie gazowej.

2. Ciepło parowania (skraplania) to ilość energii, jaką należy dostarczyć (odprowadzić), aby odparować (skroplić) 1 kilogram danej substancji. Jest to wielkość charakterystyczna dla danego rodzaju substancji. Jednostką ciepła parowania w układzie SI jest $\left[\frac{\mathrm{J}}{\mathrm{kg}}\right]$.

3. Definicję ciepła parowania możemy zapisać za pomocą wzoru: $R=\frac{Q}{m}$$$,
   gdzie:
   $R$ – ciepło topnienia;
   $m$ – masa ciała;
   $\mathrm{\Delta }E=Q$ – energia (ciepło) dostarczone do ciała.

16. Energia wewnętrzna a zmiany stanu skupienia

RGk9S5s4QiZl91

Zdjęcia przedstawiające pokrywę lodową na jeziorze, na którą świeci słońce – wyraźnie widoczne promienie słoneczne padające na powierzchnię lodu

1. Topnienie, parowanie i sublimacja to zmiany stanu skupienia, które wymagają dostarczania energii do substancji.

2. Dostarczona energia powoduje wzrost energii wewnętrznej ciała związany ze zmianą struktury wewnętrznej tej substancji – rośnie energia potencjalna wynikająca z oddziaływań wzajemnych atomów i cząsteczek.

3. Krzepnięcie, skraplanie i resublimacja to zmiany stanu skupienia, które wymagają oddawania energii przez substancję.

4. Oddana energia powoduje zmniejszenie energii wewnętrznej ciała i wiąże się ze zmianą struktury wewnętrznej substancji – maleje energia potencjalna wynikająca z oddziaływań wzajemnych atomów i cząsteczek.

Test

Zadania