R1Jg6y3iZeuDJ1

Zdjęcie przedstawia plac budowy sfotografowany zza bramy wjazdowej. W tle dwa budowane wiadukty na wysokich słupach nośnych. Na pierwszym planie po lewej stronie niebieski dźwig gąsienicowy. Po prawej stronie urządzenie podwieszone na wyciągniętym wysięgniku dźwiga. Ma ono postać płaskiej konstrukcji w kolorze niebieskim wewnątrz której znajduje się otwór o dużej średnicy. Z otworu tego wystaje koniec wbitej w ziemię grubościennej rury o ponad dwumetrowej średnicy.

1. Ruch drgający i jego przykłady

R1aaCAP6EI5J31

Fotografia przedstawiająca wahadło Foucaulta.

• Ruch drgający to taki ruch, w którym wielkości opisujące go zmieniają cyklicznie swoje wartości.

• Ruch drgający odbywa się wokół punktu zwanego położeniem równowagi.

• Szczególnymi przykładami ruchu drgającego są: ruch wahadła matematycznego i ciężarka zawieszonego na sprężynie, które wykonują drgania harmoniczne.

2. Wielkości opisujące drgania

R1JuYENx3Znip1

Zdjęcie częstościomierza

• Wielkościami opisującymi ruch drgający są:

  • amplituda drgań $A$ – największe wychylenie z położenia równowagi;

  • okres drgań$T$ – czas trwania jednego pełnego drgania; jednostka: sekunda [s];

  • częstotliwość drgań – liczba drgań w jednostce czasu; jednostka: herc [Hz].

    Częstotliwość i okres drgań są związane zależnością: $f=\frac{1}{T}$.

• Wykresem zależności położenia danego punktu od czasu w ruchu harmonicznym jest sinusoida. Z takiego wykresu można odczytać amplitudę i okres drgań.

3. Przemiany energii w ruchu drgającym

R1AImckcDY8II1

Zdjęcie kuli burzącej

• Ciało wykonujące ruch drgający posiada dwa rodzaje energii: energię kinetyczną i energię potencjalną.

• Dla wahadła matematycznego energia potencjalna to energia potencjalna grawitacji, a dla ciężarka na sprężynie – energia potencjalna sprężystości.

• Podczas drgania zmienia się zarówno wartość energii kinetycznej, jak i energii potencjalnej.

• Energia kinetyczna:

  • rośnie, gdy ciało drgające zbliża się do położenia równowagi;

  • maleje podczas oddalania się ciała od położenia równowagi;

  • osiąga największą wartość, gdy ciało przechodzi przez położenie równowagi;

  • przyjmuje wartość zero w punktach maksymalnego wychylenia z położenia równowagi.

• Energia potencjalna:

  • maleje, gdy ciało drgające zbliża się do położenia równowagi;

  • rośnie podczas oddalania się ciała od położenia równowagi;

  • osiąga największą wartość w punktach maksymalnego wychylenia z położenia równowagi;

  • przyjmuje wartość zero, gdy ciało przechodzi przez położenie równowagi.

• Suma energii kinetycznej i potencjalnej podczas drgania pozostaje stała i równa jest pracy wykonanej przez siły zewnętrzne podczas wytrącania ciała z położenia równowagi.

5. Wyznaczanie okresu drgań wahadła matematycznego

RQtQOuHo2cLOT1

Zdjęcia wahadła matematycznego i stopera

• Wyznaczanie okresu drgań wahadła matematycznego polega na zmierzeniu czasu trwania kilku lub kilkudziesięciu wahnięć i podzieleniu wyniku tego pomiaru przez liczbę wahnięć.
  $T= \frac{t_n}{n}$,
  gdzie:
  $n$ – liczba wahnięć; $t_n$ – czas trwania $n$ wahnięć.

• Okres drgań wahadła matematycznego dla małych kątów wychylenia nie zależy od amplitudy drgań. Tę właściwość wahadła nazywamy izochronizmem.

• Okres drgań wahadła matematycznego zależy od jego długości, przy czym:

  • większej długości odpowiada większa wartość okresu drgań;

  • gdy długość wahadła wzrośnie cztery razy, to okres drgań wzrośnie dwa razy.

• Okres drgań wahadła matematycznego nie zależy od masy wahadła.

6. Wyznaczanie okresu drgań ciężarka na sprężynie

RGPy1OYfJ2YR61

Zdjęcie ciężarka na spręzynie i stopera

• Aby wyznaczyć częstotliwość drgań ciężarka na sprężynie, należy zmierzyć czas trwania kilku lub kilkudziesięciu drgań i podzielić liczbę drgań przez zmierzony czas.
  $f=\frac{n}{t_n}$
  gdzie:
  $n$ – liczba drgań; $t_n$ – czas trwania $n$ drgań.

• Aby wyznaczyć okres drgań ciężarka na sprężynie, należy zmierzyć czas trwania kilku lub kilkudziesięciu drgań i podzielić zmierzony czasu przez liczbę drgań.
  $T= \frac{t_n}{n}$

• Okres drgań ciężarka na sprężynie zależy od jego masy, przy czym większej masie odpowiada większa wartość okresu drgań.

7. Fala mechaniczna

RiuWsp776BZgF1

Zdjęcie fali

• Fala mechaniczna to drgania czasteczek rozchodzące się w ośrodku sprężystym.

• Źródłem fali jest ciało drgające, które przekazuje drgania cząsteczkom ośrodka.

• Gdy w ośrodku rozchodzi się fala, cząsteczki tego ośrodka wykonują ruch drgający; każda wokół swego położenia równowagi. Ruch ten odbywa się na małej przestrzeni.

• Fala mechaniczna to drgania rozchodzące się ruchem jednostajnym w ośrodku jednorodnym. Ruch fali jest możliwy wtedy, gdy cząsteczki ośrodka przekazują sobie wzajemnie drgania.

8. Wielkości opisujące ruch falowy

RqbgOqWSIJuAL1

Fiz_gim_kl2_d6_m64_zdjęcie_8_dlugosc_fali

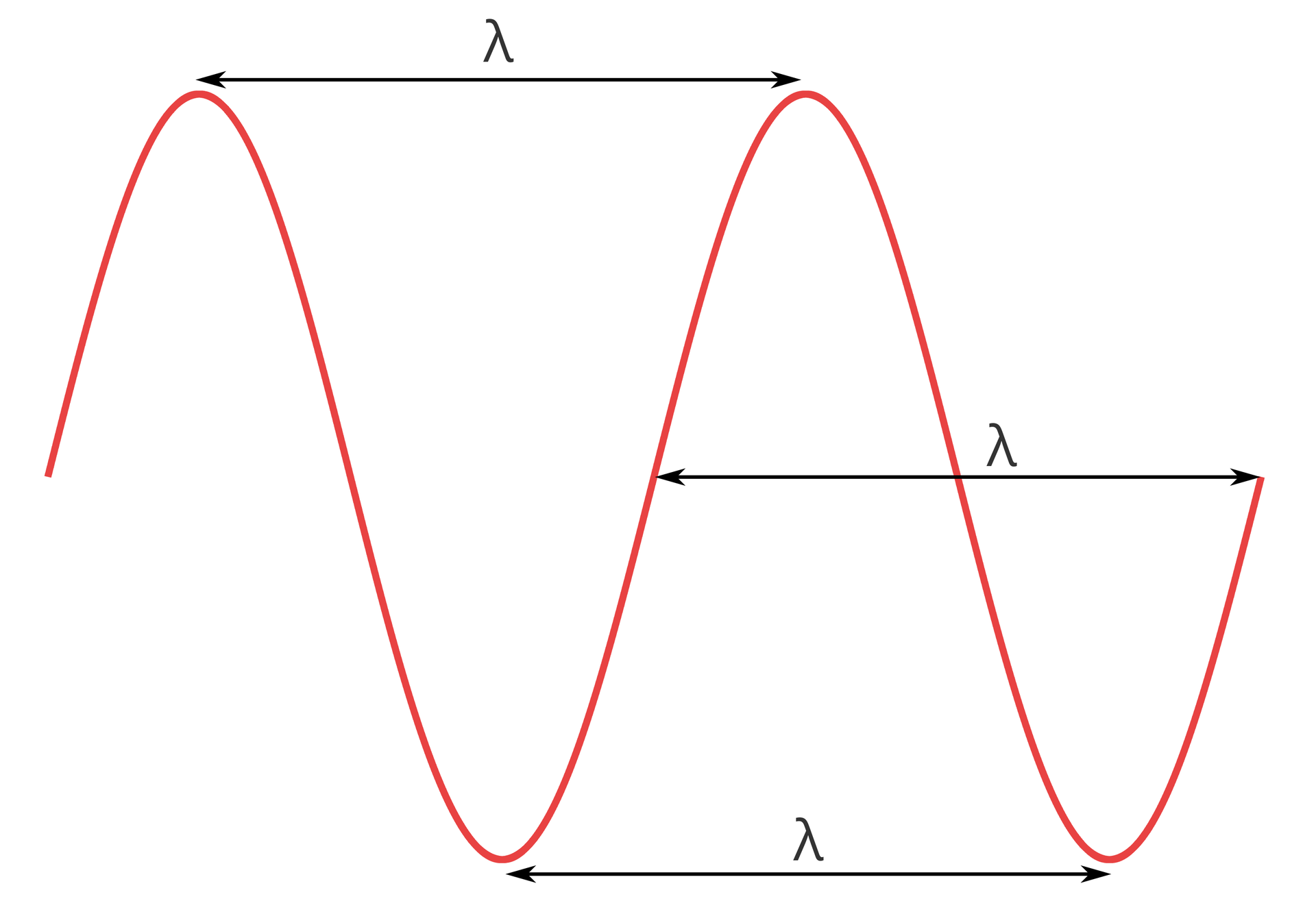
Wielkości charakteryzujące ruch falowy:

• prędkość fali $\mathrm{(v)}$ – prędkość, z jaką w ośrodku rozchodzi się zaburzenie wywołane drganiami źródła fali. Jej wielkość zależy od właściwości ośrodka; jego sprężystości i gęstości; jednostka – metr na sekundę $\left[\frac{m}{s}\right]$;

• amplituda fali $\mathrm{(A)}$ – amplituda drgań cząsteczek ośrodka, w którym rozchodzi się fala; jednostka – metr;

• okres fali $\mathrm{(T)}$ – okres drgań źródła fali, a jednocześnie okres drgań cząsteczek ośrodka, w którym rozchodzi się fala; jednostka – sekunda;

• częstotliwość fali $\mathrm{(f)}$ – częstotliwość drgań źródła fali, a jednocześnie częstotliwość drgań cząsteczek ośrodka, w którym rozchodzi się fala; jednostka – herc [Hz];

• długość fali $\mathrm{(\lambda )}$ (lambda) – odległość między dwoma sąsiednimi grzbietami (lub dwiema sąsiednimi dolinami) fali; jednostka – metr.

9. Zależności między okresem, częstotliwością, długością i prędkością fali

R1HgeEvdEqw5k1

Fiz_gim_kl2_d6_m64_zdjęcie_9_sonar

• Częstotliwość fali jest odwrotnością okresu – tak jak w opisie drgań, czyli:
  $f= \frac{1}{T}$ , $T=\frac{1}{f}$.

• Długość fali to jednocześnie droga, jaką przebywa fala w ciągu jednego okresu drgań cząsteczek ośrodka.
  $\mathrm{droga }=\mathrm{ prędkość}·\mathrm{czas}$, czyli:
  $s=v·t$ , $\lambda =v·T$ .

10. Cechy dźwięku

R1156WkUpk9Re1

Fiz_gim_kl2_d6_m64¬_zdjęcie_10_wysoki_dzwiek

• Dźwiękami nazywamy fale wytworzone przez ciała drgające z częstotliwością z zakresu od 16 Hz do 20 kHz; podany zakres ma charakter umowny, w rzeczywistości jest cechą indywidualna każdego człowieka.

• Dźwięk może być zarejestrowany przez ludzkie ucho, jeśli energia niesiona przez falę dźwiękową jest większa od progu słyszalności, a mniejsza od granicy bólu.

• Podstawowymi cechami dźwięku są:

  • wysokość – związana z częstotliwością fali: wyższy dźwięk – większa częstotliwość;

  • głośność – związana z amplitudą fali: większa amplituda – głośniejszy dźwięk;

  • barwa* – związana ze złożonością drgań źródła fali, pozwala rozróżniać brzmienie różnych instrumentów.

11. Fale stojące

R1RDne82apdVH1

Fiz_gim_kl2_d6_m64_zdjęcie_11_fala_stojąca

Fale stojące są wynikiem nałożenia się fal biegnących w przeciwne strony; składają się z:

• węzłów – miejsc, w których elementy ośrodka nie drgają;

• strzałek – miejsc, gdzie amplituda drgań elementów ośrodka jest maksymalna.

Odległość dwóch sąsiednich węzłów równa jest połowie długości fali biegnącej w ośrodku; odległość węzła od najbliższej strzałki równa jest $\frac{1}{4}$ długości fali biegnącej.

12. Instrumenty muzyczne

RgEGVd73yIOQX1

Zdjęcie sklepu o nazwie „Instrumenty muzyczne”

• Podstawowym elementem instrumentu muzycznego jest ciało drgające: struna, słup powietrza, membrana itp.

• W drgających elementach instrumentów (strunach, słupach powietrza, membranach) powstają fale stojące.

• Wysokość (częstotliwość) dźwięku emitowanego przez instrument zależy od najdłuższej (podstawowej) fali, jaka może powstać w elemencie drgającym, a ta związana jest z rozmiarami tego elementu.

• W instrumentach dętych większej długości piszczałki odpowiada mniejsza częstotliwość podstawowa, a tym samym niższy dźwięk.

• W instrumentach strunowych wysokość dźwięku zależy od:

  • długości struny: większa długość – niższy dźwięk;

  • grubości struny: cieńsza struna – wyższy dźwięk;

  • naciągu struny: większa siła naciągu – wyższy dźwięk.

13. Infradźwięki i ultradźwięki

R7StzYFibiwLe1

Fiz_gim_kl2_d6_m64_rysunek_8_nietoperz

• Infradźwiękami nazywamy fale mechaniczne o częstotliwości mniejszej od 16 Hz.

• Źródłem ultradźwięków w naturze są: grzmoty, trzęsienia ziemi, erupcje wulkanów, wodospady, wiatr, zorze polarne.

• W budynkach infradźwięki mogą powstawać w przewodach wentylacyjnych oraz w wyniku drgań różnych maszyn i urządzeń biurowych.

• Infradźwięki mają niekorzystny wpływ na organizm człowieka.

• Ultradźwięki to fale mechaniczne o częstotliwości większej niż 20 kHz.

• Ultradźwięki są wytwarzane i rejestrowane przez niektóre zwierzęta.

• Sztucznie wytworzone w generatorach fale ultradźwiękowe znalazły liczne zastosowania w terapii i diagnostyce medycznej (USG), fizykoterapii, w technice (sonary) i nauce.

• Infradźwięki i ultradźwięki nie są rejestrowane przez ludzkie ucho, ale mogą być wysyłane i odbierane przez niektóre zwierzęta.

Zadania

Test