W filmach o życiu Indian często widzimy scenę, w której indiański wojownik przykłada ucho do ziemi i na tej podstawie ocenia odległość, w jakiej znajdują się inni jeźdźcy (najczęściej wrogowie). Czy pozyskiwanie informacji w ten sposób ma coś wspólnego ze znajomością fizyki?

R1Xq7qM9OsmcZ1

Ilustracja przedstawia kompozycję fotograficzną przygotowaną na potrzeby kampanii zwalczania hałasu. W centralnej części młody mężczyzna w żółtym swetrze z rozczochranymi włosami zaciska oczy z grymasem bólu na twarzy. Po jego lewej i prawej stronie dwa duże głośniki skierowane na niego. Cały obraz jest rozmyty, co ma symbolizować drgania spowodowane głośnymi dźwiękami. — Zakres fal akustycznych odbieranych przez ucho ludzkie jako dźwięki wynosi od 16 Hz do 20 kHz. Dla dźwięku rozchodzącego się w powietrzu oznacza to fale o długości od około 21,25 metra do 1,7 cm. Jest to duża różnica, która powoduje, że dźwięki niskie (a więc o znacznych długościach fal) przenikają przez przeszkody znacznie lepiej niż fale krótkie. Właśnie dlatego podczas głośnych imprez u sąsiadów przez ściany docierają do nas przede wszystkim dźwięki basowe, wytłumione w niewielkim stopniu

Już potrafisz

podać definicję fali oraz definicje takich wielkości jak: amplituda, okres i częstotliwość, prędkość i długość fali;
opisać falę, posługując się tymi wielkościami;
zapisać wzory podające zależności między tymi wielkościami.

Nauczysz się

stosować do obliczeń zależności między okresem, częstotliwością, długością i prędkością fali.

i3VZSSFpzd_d5e131

Przykład 1

Fale na jeziorze.
Siedzący na pomoście chłopak obserwował łódkę wędkarza tkwiącą nieopodal w pewnym miejscu jeziora. Stwierdził, że regularnie co 2 sekundy łódź unosi się do góry, w miarę jak docierają do niej kolejne grzbiety fali rozchodzącej się po powierzchni jeziora. Przyglądając się fali tuż przy pomoście, zmierzył odległość między grzbietami fali – wynosiła ona 1,5 metra. Za pomocą danych z obserwacji tego chłopaka oblicz prędkość rozchodzenia się fal po powierzchni jeziora.

RIRvTm1jLa8aN1

Źródło: Tomorrow Sp.z o.o., licencja: CC BY 3.0.

Film dostępny na portalu epodreczniki.pl

Źródło: Tomorrow Sp.z o.o., licencja: CC BY 3.0.

Animacja przedstawiająca łódkę, która unosi się do góry i opada na falach

Analiza zadania:

odległość między grzbietami fali, to długość fali; oznaczamy ją grecką literą lambda;
przedział czasu upływający między kolejnymi uniesieniami łódki w górę to okres fali oznaczany literą T; w czasie równym okresowi fala przebywa drogę równą swojej długości;
fale rozchodzą się po powierzchni jeziora ruchem jednostajnym.

Dane:
T = 2 s,
lambda = 1,5 m.
Szukane:
v = ?
Prędkość rozchodzenia się fali po jeziorze obliczamy tak jak w ruchu jednostajnym, czyli
prędkość = droga/czas
$v = \frac{λ}{T} = \frac{1,5 m}{2 s} = 0,75 \frac{m}{s}$ .

Odpowiedź:
Fala obserwowana przez chłopca rozchodziła się po powierzchni jeziora z prędkością 0,75 m/s.

Przykład 2

Sonar
Sonar używany na statku emituje ultradźwięki o częstotliwości 40 kHz. Prędkość dźwięku w wodzie wynosi 1 500 m/s. Jaką długość mają fale wzbudzanie w wodzie przez ten sonar? Porównaj tę długość z wielkością ryby.

R1JBekgmfl1J01

Analiza zadania:

długość fali to odległość między grzbietami fali; oznaczamy ją grecką literą lambda;
częstotliwość fali to liczba drgań w ciągu sekundy; oznaczamy ją literą f; jest równa odwrotności okresu;
w czasie równym okresowi fala przebywa drogę równą swojej długości;
fale rozchodzą się w wodzie ruchem jednostajnym.
Dane:
f = 40 kHz = 40 000 Hz,
v = 1500 m/s.
Szukane:
lambda = ?
Obliczenia:
Korzystając ze wzoru na drogę w ruchu jednostajnym, możemy zapisać:
droga = prędkość ∙ czas,
czyli
$λ = v \cdot T$ ,
ale okres równy jest odwrotności częstotliwości ( $T = \frac{1}{f}$ ),
zatem długość fali
$λ = v \cdot T = \frac{v}{f} = \frac{1 500 \frac{m}{s}}{40 000 Hz} = 0,0375 m = 3,75 cm \approx 4 cm$ .
Odpowiedź:
Długość fali wzbudzanej przez sonar w wodzie wynosi około 4 cm. Jest to porównywalne z wielkością małej rybki.

Przykład 3

Stukot końskich kopyt to źródło dźwięku. Dźwięk ten może rozchodzić się zarówno w powietrzu, jak i w ziemi (skale, glebie). Szybkość rozchodzenia się dźwięku jest różna w różnych ośrodkach. W powietrzu wynosi 340 m/s, a w skałach wapiennych – 3 400 m/s. Obserwator może więc zarejestrować dźwięk docierający do niego przez skałę, a następnie przez powietrze. O ile później usłyszy on dźwięk rozchodzący się w powietrzu, jeśli jeździec znajduje się w odległości 1 kilometra od obserwatora?

R7DgtnAI5gV1m1

Indianin — Źródło: ContentPlus, licencja: CC BY 3.0.

Analiza zadania:
Znamy prędkość dźwięku w powietrzu – oznaczmy ją symbolem $v_{p}$ , oraz prędkość dźwięku w skale – oznaczmy ją $v_{s}$ .
Znamy długość drogi pokonywanej przez dźwięk – oznaczmy ją symbolem s.
Wiemy, że w jednorodnym ośrodku dźwięk rozchodzi się ruchem jednostajnym.
Dane:
s = 1 km =1000 m,
vIndeks dolny p= 340 m/s,
vIndeks dolny s = 3400 m/s.
Szukane:
deltat = ?
Za pomocą wzoru na drogę w ruchu jednostajnym ( $s = v \cdot T$ ) możemy obliczyć, jak długo biegnie dźwięk od jeźdźca do obserwatora najpierw przez skałę:
$s = v_{s} \cdot t_{s} / : v_{s}$ ,
$t_{s} = \frac{s}{v_{s}} = \frac{1 000 m}{3 400 \frac{m}{s}} = 0,29 s$ ,
a następnie przez powietrze:
$s = v_{p} \cdot t_{p} / : v_{p}$
$t_{p} = \frac{s}{v_{p}} = \frac{1 000 m}{340 \frac{m}{s}} = 2,9 s$ .
Różnica czasów wynosi więc:
$Δ t = t_{p} - t_{s} = 2,9 s - 0,29 s = 2,61 s$ .
Odpowiedź:
Dźwięk rozchodzący się w skałach dociera do obserwatora 10 razy szybciej niż przez powietrze i przy odległości 1 km będzie to o 2,6 sekundy wcześniej.

Polecenie 1

Na podstawie opisanego powyżej przykładu z Indianinem powiedz, czy wspomniany we wstępie filmowy Indianin korzysta ze znajomości fizyki podczas śledzenia ruchów przeciwnika?

Ćwiczenie 1

R8kzKRFrijDXE1

Jak zmieni się długość i częstotliwość fali przechodzącej z powietrza do ceglanej ściany? Prędkość fali w cegle jest 10 razy większa niż w powietrzu.

Częstotliwość nie zmieni się, a długość fali wzrośnie 10 razy.
Częstotliwość zmaleje 10 razy, a długość fali wzrośnie 10 razy.
Częstotliwość wzrośnie 10 razy, a długość fali zmaleje 10 razy.
Częstotliwość nie zmieni się, a długość fali zmaleje 10 razy.
Długość fali nie zmieni się, a częstotliwość wzrośnie 10 razy.
Długość fali nie zmieni się, a częstotliwość zmaleje 10 razy.
Ani częstotliwość, ani długość fali nie ulegną zmianie.

Źródło: Helena Nazarenko-Fogt <Helena.Nazarenko-Fogt@up.wroc.pl>, licencja: CC BY 3.0.

Ćwiczenie 2

R1PKiQnlCGRBf1

Struna gitary drga z częstotliwością 100 Hz. Które z poniższych twierdzeń jest prawdziwe, a które fałszywe?

	Prawda	Fałsz
Częstotliwość drgań tej struny to 1 kHz.	□	□
Okres drgań tej struny to 0,01 s.	□	□
Jeśli struna drgałaby z większą częstotliwością, to emitowany przez nią dźwięk rozchodziłby się z większą prędkością.	□	□
Częstotliwość drgań tej struny to 0,1 kHz.	□	□
Okres drgań tej struny to 0,1 s.	□	□
Mocniejsze szarpnięcie struny spowoduje wzrost amplitudy jej drgań.	□	□
Mocniejsze szarpnięcie struny spowoduje wzrost częstotliwości jej drgań.	□	□

Źródło: Helena Nazarenko-Fogt <Helena.Nazarenko-Fogt@up.wroc.pl>, licencja: CC BY 3.0.

i3VZSSFpzd_d5e312

Podsumowanie

Podstawowe zależności między wielkościami fizycznymi opisującymi ruch falowy:
- częstotliwość fali równa jest odwrotności okresu drgań cząsteczek ośrodka,
  $f = \frac{1}{T}$ ,
  czyli
  $T = \frac{1}{f}$
  Oznacza to, że znając okres drgań, zawsze możemy obliczyć częstotliwość i odwrotnie;
- długość fali równa jest drodze przebytej przez falę w czasie równym okresowi tej fali, czyli:
  $λ = v \cdot T = \frac{v}{f}$
  Z tego równania możemy obliczyć jedną z trzech wielkości, gdy dwie pozostałe znamy.
W ośrodku jednorodnym fala rozchodzi się ze stałą prędkością, czyli ruchem jednostajnym.
Prędkość fali nie zależy ani od jej częstotliwości, ani od amplitudy fali, tylko od rodzaju (właściwości) ośrodka.
Gdy fala przechodzi z jednego ośrodka do drugiego, to nie zmienia się jej częstotliwość, tylko prędkość i długość.

Praca domowa

Polecenie 2.1

Skala głosu Violetty Villas rozciągała się od częstotliwości $f_{1} = 130 Hz$ (małe c w skali muzycznej) do wartości $f_{2} = 3 500 Hz$ (a czterokreślne w skali muzycznej). Oblicz największą i najmniejszą długość fali dźwiękowej powstającej w powietrzu na koncertach tej śpiewaczki.

Polecenie 2.2

Liść leżący na falującej w stawie wodzie wykonuje wahania w górę i w dół z częstotliwością 6 wahnięć w ciągu pół minuty. Fala przesuwa się po powierzchni stawu z szybkością 3 cm/s. Oblicz odległość między grzbietami tej fali.

Polecenie 2.3

RTUKXGNAnMIIt1

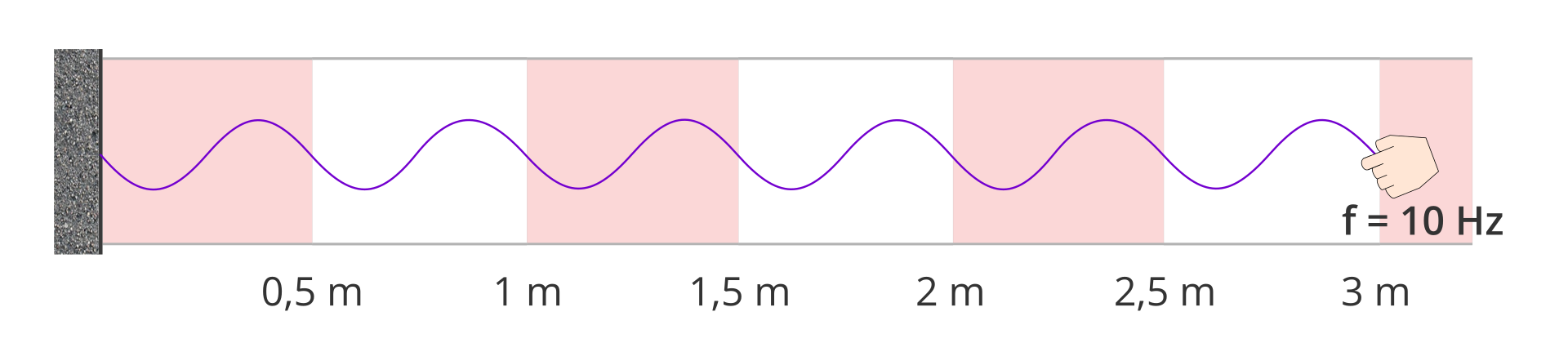
Fala na sznurze — Źródło: Krzysztof Jaworski, Vanderlindenma (https://commons.wikimedia.org), licencja: CC BY-SA 3.0.

Powyższy rysunek przedstawia falę wytworzoną na sznurze. Drgania odbywają się z częstotliwością 10 Hz. Oblicz prędkość, z jaką biegnie tak wzbudzona fala.

Polecenie 2.4

Nietoperz emituje falę ultradźwiękową, która w powietrzu osiąga długość 4 mm. Wiedząc, że dźwięk w powietrzu biegnie z szybkością 340 m/s, oblicz częstotliwość i okres fali emitowanej przez nietoperza.

i3VZSSFpzd_d5e394

Słowniczek

sonar (echosonda)

– urządzenie wykorzystujące fale dźwiękowe i ultradźwiękowe do pomiaru odległości, prędkości i wykrywania kształtu obiektów zanurzonych w wodzie, pływających po powierzchni wody lub będących powietrzu. Działanie polega na wysyłaniu fali w kierunku badanego obiektu, a następnie rejestrowaniu i analizowaniu cech fali odbitej od badanego obiektu; nazwa jest skrótem angielskiego określenia „SOund Navigation And Ranging” (tłum. nawigacja dźwiękowa i pomiar odległości).

Ultradźwięki i infradźwięki

Podsumowanie wiadomości o ruchu drgającym i falach

Stosowanie zależności między okresem i częstotliwością oraz prędkością i długością fal w obliczeniach

Podsumowanie

Słowniczek