R1Em2bcMxdI9E1

Zdjęcie przedstawia jadący po torach szybki pociąg pasażerski uwieczniony w momencie mijania akwenu wodnego. Z tego powodu obraz pociągu odbija się w tafli wodnej. Daleko w tle widoczne są zabudowania mieszkalne i wzgórza, a nad nim czyste niebo.

1. Ruch jest względny

RZ9FPNQtWhH341

Zdjęcie przedstawia wnętrze przedziału w pociągu. Po lewej i po prawej krzesła obite wielkokolorowym materiałem. Na wprost okno. Za oknem widać rozmazane kontury zielonych drzew.

1. Ruch i spoczynek są pojęciami względnymi. Można jednocześnie być w ruchu względem jednego ciała i w spoczynku względem innego. Pasażerowie jadącego pociągu są w spoczynku względem siebie i jednocześnie poruszają się względem drzew za oknem.

2. Ruch polega na zmianie położenia ciała względem wybranego układu odniesienia, np. samochodu względem słupa latarni, Księżyca względem Ziemi itp. Zmiana ta zachodzi w czasie.

2. Układ odniesienia

R1IbdrpI62YwO1

Zdjęcie przedstawia drogę szybkiego ruchu. Droga dwupasmowa, oddzielona pasem zieleni. Wzdłuż drogi, po obu stronach rosną drzewa. Dominują drzewa iglaste. W tle jasne niebo. Na drodze znajduje się kilkanaście samochodów. Na jednym z samochodów narysowano układ współrzędnych. Początek układu znajduje się na środku maski.

1. Układ odniesienia to dowolnie wybrane ciało lub ciała, względem których określamy zmiany położenia badanego ciała. Dla ruchów w pobliżu powierzchni Ziemi najczęściej wybieranym układem odniesienia są Ziemia lub jakiś punkt na jej powierzchni trwale z nia związany.

2. Szczegółowy opis ruchu za pomocą zależności matematycznych wymaga powiązania go z układem odniesienia i układem współrzędnych.

3. Wielkości opisujące ruch

R1PqlX7eu36LH1

Zdjęcie przedstawia krętą drogę w górach. Droga staje się tym bardziej kręta, im wyższa wysokość góry.

Podstawowe wielkości fizyczne opisujące ruch to:

1. tor ruchu, czyli ślad zakreślony przez poruszające się ciało;

2. droga – długość toru;

3. prędkość;

4. przyspieszenie.

Jednostką drogi (s) w układzie SI jest metr.

4. Prędkość

R1JuyHCNjhOwg1

Zdjęcie przedstawia tarczę prędkościomierza w samochodzie. Tło i tarcza czarne. Tarcza okrągła. Liczby i litery podświetlane. Skala od 0 do 220, co 20, również podświetlana. U góry tarczy, po środku widać litery „km/h”. Czerwona wskazówka spoczywa na liczbie 0. Na samym dole cyfrowy wyświetlacz Na nim liczby 12 1662 oraz 268,1.

1. Prędkość to wielkość fizyczna, która informuje nas, jaką drogę przebywa ciało w danej jednostce czasu.

2. Jednostką prędkości w układzie SI jest metr na sekundę $\left[\frac{\mathrm{m}}{\mathrm{s}}\right]$. W życiu codziennym częściej posługujemy się jednostką taką jak kilometr na godzinę $\left[\frac{\mathrm{km}}{\mathrm{h}}\right]$. Jednostki te możemy przeliczać – korzystamy wtedy z zależności: $1\mathrm{}\frac{\mathrm{km}}{\mathrm{h}}=\frac{\mathrm{1000\; m}}{\mathrm{3600\; s}}=\frac{\mathrm{10\; m}}{\mathrm{36\; s}}=\mathrm{0,277}\mathrm{}\frac{\mathrm{m}}{\mathrm{s}}$
   $$$1\frac{\mathrm{m}}{\mathrm{s}}=\frac{\mathrm{0,001}}{\frac{1}{3600}}\frac{\mathrm{km}}{\mathrm{h}}=\mathrm{3,6}\frac{\mathrm{km}}{\mathrm{h}}$

3. W fizyce wyróżniamy prędkość średnią i chwilową.

4. Prędkość średnią obliczamy za pomocą wzoru:
   $v_{\mathrm{śr}}=\frac{s}{t}$
   gdzie:
   $v_{\mathrm{śr}}\left[\frac{\mathrm{m}}{\mathrm{s}}\right]$ – prędkość średnia;
   $\mathrm{s }\left[\mathrm{m}\right]$– droga przebyta przez ciało;
   $t\left[\mathrm{s}\right]$ – czas trwania ruchu.

5. Prędkość chwilowa to prędkość ciała w danym momencie ruchu. Prędkość chwilową wskazują prędkościomierze, np. samochodowe.

5. Wyznaczanie prędkości

RgcWXvC1Snawu1

Schemat przedstawiający ludzika ze stoperem w ręku, maszerującego po taśmie mierniczej.

Aby wyznaczyć prędkość jakiegoś ciała, należy zmierzyć dwie wielkości:

• drogę przebytą przez to ciało (za pomocą przyrządu do pomiaru odległości);

• przedział czasu, w którym ta droga została przebyta (mierzymy go stoperem).

Prędkość średnią obliczamy ze wzoru:

Piechur maszerujący po płaskim terenie porusza się z prędkością około 1,4 m/s$\approx$ 5 km/h.

6. Ruch jednostajny prostoliniowy

RQ0iUB1u5QQqM1

Zdjęcie przedstawia samolot na tle nieba. Niebo intensywnie niebieskie. Samolot widoczny z oddali. Samolot bały, widok od dołu. Za samolotem dwie długie, białe smugi.

1. Ruch prostoliniowy to ruch, którego torem jest linia prosta.

2. Ruch jednostajny to ruch, w którym ciało porusza się ze stałą prędkością.

3. W ruchu jednostajnym prostoliniowym ciało w przebywa jednakowe odcinki drogi w równych odstępach czasu.

4. W ruchu jednostajnym prostoliniowym prędkość średnia i chwilowa są sobie równe.

5. Droga przebyta przez ciało w ruchu jednostajnym jest wprost proporcjonalna do czasu trwania ruchu. Obliczamy ją ze wzoru:
   $s=v·t$
   gdzie:
   $\mathrm{v }\left[\frac{\mathrm{m}}{\mathrm{s}}\right]$ – wartość prędkości ciała;
   $s\mathrm{[m]}$ – droga przebyta przez ciało;
   $t\mathrm{[s]}$ – czas ruchu ciała.

7. Wykresy zależności drogi i prędkości od czasu w ruchu jednostajnym

RJ5JTtZarXi8G1

Schemat przedstawia wykres. Tło białe. Niebieska linia łamana na układzie współrzędnych. Początek w trzeciej ćwiartce, koniec w pierwszej. Pomiędzy drugą a pierwszą, linia równoległa do osi odciętych.

Wykres to graficzny sposób przedstawienia zależności między wielkościami fizycznymi.
Wykres zależności drogi od czasu opisujemy symbolem s(t).
W ruchu jednostajnym wykresem s(t) jest prosta, nachylona lub równoległa do osi czasu.

RMbtcTByOYhtw1

Schemat przedstawia wykres. Tło białe. Oś odciętych opisana jako „t,”. Oś rzędnych opisana jako v”. Na wykresie widoczne dwa odcinki: niebieski i czerwony. Oba mają początek w początku układu współrzędnych. Odcinek niebieski leży względem osi odciętych pod kątem ok. 45 stopni. Odcinek czerwony leży względem osi odciętych pod ostrzejszym kątem.

Wykresem zależności prędkości od czasu, opisywanym symbolem v (t), w tym ruchu jest prosta równoległa do osi czasu.

RsYiEysXFPQ2w1

Schemat przedstawia wykres zależności przyspieszenia od czasu. Oś odciętych opisana jako „t [s]”. Oś rzędnych opisana jako „v [m/s]”. Na wykresie widoczny niebieski odcinek. Odcinek równoległy do osi odciętych. Początek na osi rzędnych, w około połowie jej wysokości. Koniec prawie na wysokości grotu poziomej strzałki.

Pole prostokąta pod wykresem v(t) jest liczbowo równe przebytej drodze.

R11eA7u2n9kDz1

Ilustracja przedstawia wykres zależności prędkości od czasu. Tło białe. Oś odciętych opisana jako „t [s]”. Oś rzędnych opisana jako „v [m/s]”. Na wykresie niebieski prostokąt. Lewy dolny róg leży w początku układu współrzędnych. Krótszy bok leży na osi rzędnych. Dłuższy bok leży na osi odciętych.

8. Ruch zmienny

RNr4GD58ADJxQ1

Ilustracja przedstawia hamującego ptaka. Tło białe. Pióra niebieskie, dziób i nogi żółte. Duże oczy, dziób rozwarty. Szpony uniesione, pod stopami grunt, którą ptak przesunął podczas hamowania.

1. Ruch zmienny to taki, w którym zmienia się wartość prędkości.

2. Może on być:

   1. przyspieszony – jeśli w jego trakcie prędkość ciała rośnie (rozpędzanie się, przyspieszanie);

   2. opóźniony – jeśli prędkość ciała maleje (hamowanie, zwalnianie).

3. W ruchu zmiennym prędkość chwilowa różni się od prędkości średniej.

9. Symbol Δdelta (delta) i jego znaczenie w fizyce

Rh4U9FdDdRf8K1

Ilustracja przedstawia symbol greckiej litery ∆ delta. Tło białe. Na środku duży trójkąt. Kontury czarne, wnętrze białe. Trójkąt równoramienny. Kontur prawego ramienia grubszy niż pozostałych boków.

1. Grecką literę $∆$ (delta) stosuje się we wzorach fizycznych do oznaczania zmian (przyrostów, ubytków, różnic) wielkości fizycznych. Ta litera oznacza zmianę, ale tylko w towarzystwie symbolu wielkości fizycznej. Przez zmianę rozumie się na ogół różnicę między wartością danej wielkości na końcu obserwacji i na początku obserwacji.

2. Ta różnica może mieć wartość dodatnią, ujemną lub równą zero. Na określenie zmian różnych wielkości używa takich określeń jak np. odstęp lub przedział czasu, zmiana wysokości, różnica temperatur.

3. Przykładowo: $∆v$ oznacza zmianę (przyrost lub spadek) wartości prędkości, $∆t$ – przedział czasu, $∆T$ – różnicę temperatur, $∆h$ – zmianę wysokości itd.

4. Zmiana prędkości: $∆v=v_k-v_p$$$to różnica między wartością prędkości końcowej i początkowej. Zmiana ta jest dodatnia w ruchu przyspieszonym, a ujemna – w ruchu opóźnionym.

10. Przyspieszenie

R1HXUNElND5Jb1

Zdjęcie przedstawia sportowy samochód. Samochód srebrnoszary. Znajduje się na asfaltowej drodze. Z okolic tylnych kół wydobywa się smuga dymu.

1. Przyspieszenie to wielkość fizyczna, która mówi nam, ile wynosi zmiana prędkości ciała w jednostce czasu.

2. Przyspieszenie obliczamy ze wzoru:
   $\mathrm{przyspieszenie}=\frac{\mathrm{zmiana\; prędkości}}{\mathrm{przedział czasu}}$
   $a= \frac{∆v}{∆t}$
   gdzie:
   $∆v$ – zmiana (przyrost lub spadek) wartości prędkości;
   $∆t$ – przedział czasu, w którym nastąpiła ta zmiana.

3. Jednostką przyspieszenia w układzie SI jest $\left[\frac{\mathrm{m}}{{\mathrm{s}}^2}\right]$.

4. Przyspieszenie o wartości np. $2\frac{\mathrm{m}}{{\mathrm{s}}^2}$ informuje nas, że prędkość ciała zmienia się co sekundę o $2\frac{\mathrm{m}}{{\mathrm{s}}^{}}$.

11. Ruch przyspieszony w sposób jednostajny

RB18UudAgqpi51

Ruch jednostajnie przyspieszonyIlustracja przedstawia wykres kolumnowy. Tło jasne. Na dole czarna, pozioma linia. Wzdłuż linii umieszczono sześć kolumn. Kolumny niebieskie, prostokątne. Wszystkie mają taką samą długość krótszego boku. Kolumny od najniższej do najwyższej (według dłuższego boku). Nad wszystkimi kolumnami poprowadzono wznoszącą się, czerwoną strzałkę. Grot zwrócony do prawego, górnego rogu ilustracji.

1. Ruchem jednostajnie przyspieszonym prostoliniowym (przyspieszonym w sposób jednostajny) nazywamy taki ruch, w którym przyspieszenie jest stałe, co oznacza, że prędkość rośnie o jednakową wartość w równych odstępach czasu (np. co 1 sekundę), a torem ruchu jest linia prosta.

2. Prędkość końcową, jaką osiągnęło ciało w ruchu jednostajnie przyspieszonym prostoliniowym z prędkością początkową $v_0=0\frac{\mathrm{m}}{\mathrm{s}}$, możemy obliczyć za pomocą wzoru:
   $v_k=a·∆t$
   gdzie:
   $v_k\left[\frac{m}{s}\right]$ – prędkość końcowa ciała.

3. Gdy przed rozpoczęciem ruchu ciało znajdowało się w spoczynku ($v_0=0\frac{\mathrm{m}}{\mathrm{s}}$), drogę w ruchu jednostajnie przyspieszonym prostoliniowym obliczamy za pomocą wzoru:
   $s= \frac{1}{2}· a·t^2$
   gdzie:
   $s\left[\mathrm{m}\right]$ – droga;
   $a\left[\frac{\mathrm{m}}{{\mathrm{s}}^2}\right]$ – przyspieszenie;
   $t\left[\mathrm{s}\right]$ – czas ruchu ciała.

12. Wykresy w ruchu jednostajnie przyspieszonym

R1Y92RHmqkovI1

Ilustracja przedstawia wykres. Tło białe. Oś odciętych opisana jako „x”. Oś rzędnych opisana jako „y”. Na wykresie znajduje się niebieska linia. Początek w początku układu współrzędnych. Linia przyjęła kształt połowy paraboli z ramieniem skierowanym do góry. Najniższy punkt paraboli przypada na początek układu współrzędnych.

1. Wykresem zależności przyspieszenia od czasu $a\left(t\right)$ jest prosta równoległa do osi czasu. Zaznaczone pole jest równe zmianie wartości prędkości.

   ROcmD9dK4uTRf1

   Ilustracja przedstawia wykres. Tło białe. Oś odciętych opisana jako „t”. Oś rzędnych opisana jako „a (t)”. Na wykresie pomarańczowy odcinek. Odcinek równoległy do osi odciętych. Początek na osi rzędnych, w około trzech czwartych jej wysokości, w punkcie „a”. Na osi odciętych zaznaczono punkt „t” (w około czterech piątych jej długości). Na wykresie zaznaczono obszar pod odcinkiem. Tworzy on prostokąt. W środku umieszczono wzór: ∆v = a • t.

   

2. Wykresem zależności prędkości od czasu $v\left(t\right)$ w ruchu jednostajnie przyspieszonym jest prosta nachylona do osi czasu.

   R1LL5d10ICcvo1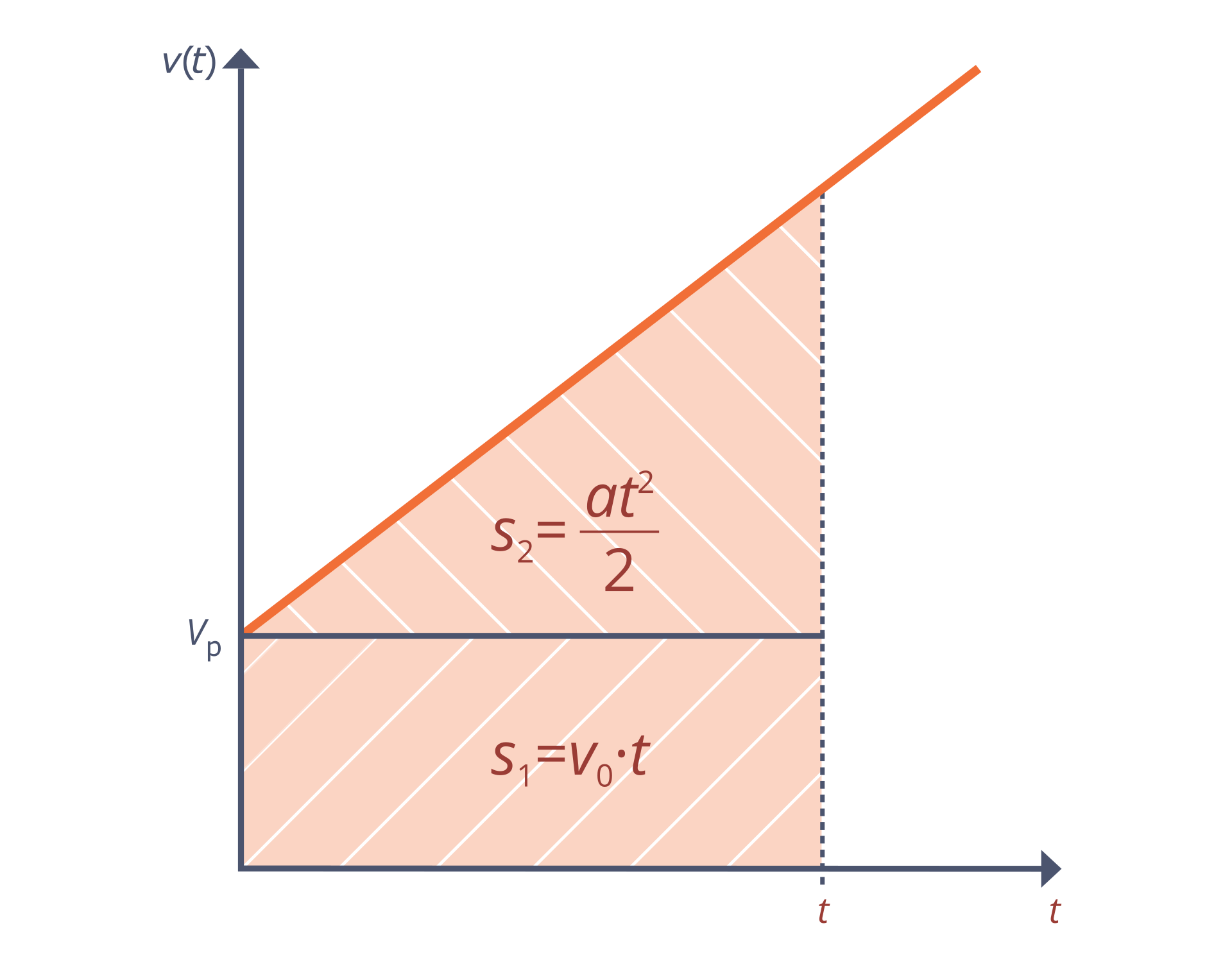

   Schemat przedstawia wykres. Tło białe. Oś odciętych opisane „t”. Oś rzędnych opisane „v (t)”. Na wykresie narysowano pomarańczowy prostokąt i trójkąt prostokątny. Na osi odciętych zaznaczono punkt t, na osi rzędnych punkt vk. Prostokąt lewy dolny róg ma w początku układu współrzędnych. Wysokość od (0, 0) do (0, vk). Dłuższa przyprostokątna trójkąta pokrywa się z dłuższym, górnym bokiem prostokąta. Punkt vk jest wierzchołkiem trójkąta. Trójkąt z prostokątem tworzą trapez prostokątny. Krótsza podstawa leży na osi odciętych i ma długość vk. Wewnątrz prostokąta napisano wzór: s₁ = vk • t. Wewnątrz trójkąta napisano wzór: S₂ = (a • t do kwadratu)/2.

   

3. Pole figury pod wykresem zależności prędkości od czasu odpowiada wartości drogi przebytej przez ciało.

13. Zadania

14. Test