Pole powierzchni graniastosłupa

Siatka graniastosłupa

Rozcinając kartonowy model graniastosłupa i rozprostowując go na płaszczyźnie, otrzymujemy siatkę graniastosłupa. Siatka składa się z prostokątów (lub równoległoboków) będących ścianami bocznymi i dwóch wielokątów, będących podstawami.

Przykłady siatek graniastosłupów prostych:

RITxTgjxvvO9Q1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1bmXcocQZCId1

R19h28wgDtSQo1

R54Vz4TRMuxwM1

Prostopadłościan jest trójwymiarową bryłą przypominająca klocek. Składa się on z czterech prostokątnych ścian połączonych ze sobą bokami dokładnie w taki sam sposób jak na przykład ściany pokoju. Bryła ta posiada również dwie podstawy: górną i dolną, które w naszym porównaniu byłyby sufitem i podłogą pokoju. Prostopadłościan możemy rozłożyć na płasko, uzyskując siatkę składającą się sześciu figur: dwóch par identycznych prostokątów, czyli przeciwległych ścian oraz dwóch identycznych prostokątów będących podstawami. Oznacza to, że nie wszystkie ściany bryły muszą być identyczne. Prostopadłościan może bowiem być „spłaszczony”.
Układ siatki nie jest przypadkowy. Nie każde trzy pary identycznych prostokątów mogą utworzyć prostopadłościan. Przykłady konstrukcji siatek przedstawimy poniżej. Dla wygody określmy, że nasz prostopadłościan składa się z pary identycznych ścian A, pary identycznych ścian B oraz podstawy górnej i dolnej. Oczywiście ściany A i B mogą być w szczególności identyczne, jeśli tylko podstawy są kwadratami.
1. Weźmy górną podstawę bryły. Do jej dolnego boku przylega ściana A. Po bokach tej ściany znajdują przylegające do niej ściany B. Do dolnego boku ściany A przylega swoim górnym bokiem podstawa dolna, a do dolnego boku dolnej podstawy przylega ściana A.
2. Drugim przykładem siatki może być siatka tej samej bryły, której opis zaczniemy od ściany B. Do jej prawego boku przylega ściana A. Do prawego boku ściany A przylega druga ściana B. Do prawego boku drugiej ściany B przylega druga ściana A, do której górnego i dolnego boku przylegają obie podstawy.

Graniastosłup sześciokątny jest trójwymiarową bryłą, która składa się z sześciu prostokątnych ścian połączonych ze sobą bokami. Bryła ta posiada również dwie podstawy: górną i dolną. Taki graniastosłup możemy rozłożyć na płasko, uzyskując siatkę składającą się z ośmiu figur: dwóch identycznych sześciokątów, czyli przeciwległych podstaw oraz sześciu identycznych prostokątów, będących ścianami bocznymi.
Układ siatki nie jest przypadkowy. Nie z każdych dwóch sześciokątów i sześciu prostokątów możemy ułożyć siatkę graniastosłupa sześciokątnego. Przykłady konstrukcji siatek przedstawimy poniżej. Dla wygody ponumerujemy ściany boczne sześcianu liczbami od 1 do 6.
1. Weźmy górną podstawę bryły. Do jej dolnego boku przylega ściana 1 . Po prawej stronie tej ściany znajdują się kolejno przylegające ściany 2, 3, 4, 5 i 6. Do dolnego boku ściany 1 przylega swoim górnym bokiem podstawa dolna.
2. Drugim przykładem siatki może być siatka tej samej bryły, której opis zaczniemy od górnej podstawy. Do każdego boku podstawy przylega jedna ściana boczna, a do dolnego boku dowolnej ze ścian przylega dolna podstawa.

Ważne!

Siatką prostopadłościanu jest figura płaska, z której można złożyć model prostopadłościanu. Siatka prostopadłościanu składa się z trzech par przystajacych prostokątów.

R17lVU8ZOzKpH1

R1RXkaFe6bD841

Sześcian jest szczególnym przypadkiem prostopadłościanu, którego wszystkie ściany są identyczne i są kwadratami.
Sześcian możemy rozłożyć na płasko, uzyskując siatkę składającą się sześciu takich samych kwadratów. Tak samo jak w przypadku prostopadłościanu, układ siatki nie jest przypadkowy. Nie każde sześć identycznych kwadratów może utworzyć sześcian. Przykłady konstrukcji siatek przedstawimy poniżej. Dla wygody ponumerujemy ściany boczne sześcianu liczbami od 1 do 4.
1. Weźmy górną podstawę bryły. Do jej dolnego boku przylega ściana 1 . Po prawej stronie tej ściany znajdują się kolejno przylegające ściany 2, 3 i 4. Do dolnego boku ściany 1 przylega swoim górnym bokiem podstawa dolna.
2. Drugim przykładem siatki może być siatka tej samej bryły, której opis zaczniemy od górnej podstawy. Do jej prawego boku przylega ściana 1, do lewego boku przylega ściana 2, do górnego boku przylega ściana 3, a do dolnego boku przylega ściana 4 .Do dolnego boku ściany 4 przylega dolna podstawa.

Ważne!

Przykłady siatek prostopadłościanów.

R6JvrnRe8D7v51
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RKDHS2NKhIzh71
Rysunek siatki prostopadłościanu złożonej z trzech par jednakowych prostokątów. Do prawej krawędzi najmniejszego prostokąta przylega największy prostokąt. Do prawej krawędzi tego największego prostokąta przylega drugi najmniejszy prostokąt. Do prawej krawędzi drugiego najmniejszego prostokąta przylega drugi największy prostokąt. Do górnej i dolnej krawędzi drugiego największego prostokąta przylegają mniejsze prostokąty, które są większe od najmniejszych.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
RRAEyKgIzrPP41
Rysunek siatki prostopadłościanu złożonej z trzech par jednakowych prostokątów. Do prawej krawędzi najmniejszego prostokąta przylega największy prostokąt. Do prawej krawędzi tego największego prostokąta przylega drugi najmniejszy prostokąt, a do jego górnej krawędzi przylega średni prostokąt. Do prawej krawędzi drugiego najmniejszego prostokąta przylega drugi największy prostokąt. Do dolnej krawędzi drugiego największego prostokąta przylega drugi średni prostokąt.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.
REycyJtxikr1a1
Rysunek siatki prostopadłościanu złożonej z trzech par jednakowych prostokątów. Do prawej krawędzi najmniejszego prostokąta przylega największy prostokąt, a do jego górnej krawędzi przylega średni prostokąt. Do prawej krawędzi tego największego prostokąta przylega drugi najmniejszy prostokąt, a do jego dolnej krawędzi przylega średni prostokąt. Do prawej krawędzi drugiego najmniejszego prostokąta przylega drugi największy prostokąt.
Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przykład 1

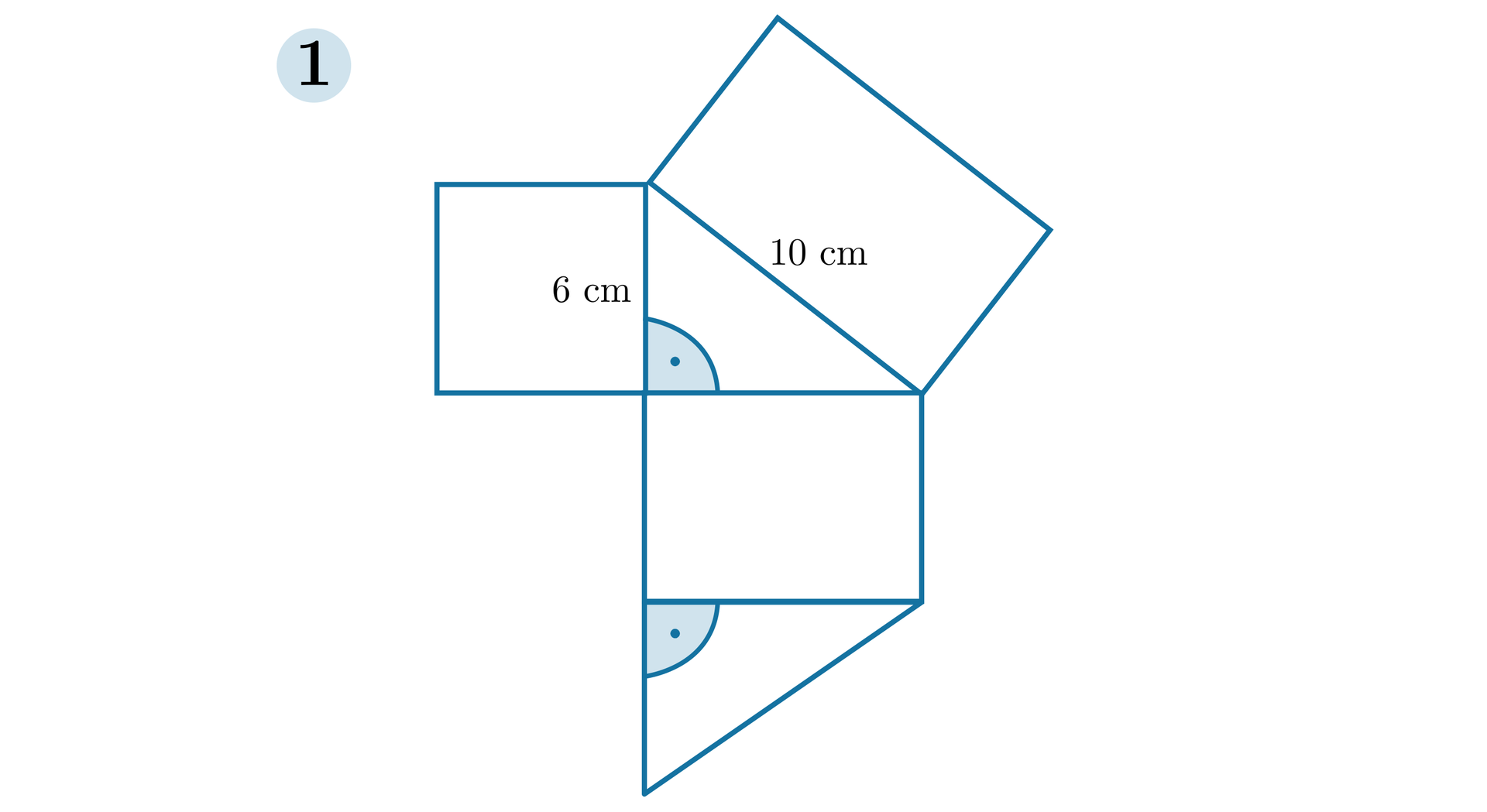
Rysunek przedstawia siatkę graniastosłupa prostego. Obliczymy sumę długości krawędzi tego graniastosłupa.

RZZWGaylFl8dp1

Rysunek siatki graniastosłupa, która składa się z dwóch trójkątów prostokątnych o dłuższych przyprostokątnych równych 24 cm i przeciwprostokątnych równych 25 cm, które stanowią podstawy, oraz z trzech prostokątów, które stanowią ściany boczne. Każdy z prostokątów ma dwa boki długości 9 cm. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wszystkie krawędzie boczne graniastosłupa są równe i mają długość $9 cm$ . Suma ich długości jest równa

3 \cdot 9 cm = 27 cm

Podstawą jest trójkąt prostokątny o jednej z przyprostokątnych długości $24 cm$ i przeciwprostokątnej długości $25 cm$ . Korzystając z twierdzenia Pitagorasa, obliczymy długość $x$ drugiej przyprostokątnej.

24^{2} + x^{2} = 25^{2}

576 + x^{2} = 625

x^{2} = 49

x = \sqrt{49} = 7

x = 7 cm

Obliczamy sumę długości krawędzi podstaw.

2 \cdot (24 + 7 + 25) cm = 112 cm

Obliczamy sumę długości wszystkich krawędzi.

27 cm + 112 cm = 139 cm

Odpowiedź:

Suma długości wszystkich krawędzi graniastosłupa wynosi $139 cm$ .

Pole powierzchni graniastosłupa

Znajomość siatki graniastosłupa pozwala wyznaczyć jego pole powierzchni. Jest ono równe sumie pól wszystkich wielokątów, z których składa się siatka.

RakstiyKlRQHs1

Rt6YvFP5ZvwVp1

Siatka każdego sześcianu składa się z sześciu takich samych kwadratów. Przyjmując, że długość boku jednego takiego kwadratu wynosi $a$ , możemy wyznaczyć wzór ogólny na pole powierzchni sześcianu. Będzie to pole powierzchni jednego kwadratu pomnożone przez ilość kwadratów, czyli $P = 6 \cdot a^{2}$ .

Siatka każdego prostopadłościanu składa się z trzech par prostokątów o takich samych wymiarach. Przyjmując, że wymiary jednej pary prostokątów to $a$ na $b$ , wymiary drugiej pary prostokątów to $b$ na $c$ , a wymiary trzeciej pary prostokątów to $a$ na $c$ , możemy wyznaczyć wzór ogólny na pole powierzchni prostopadłościanu. Będzie to suma trzech składników, każdy składnik to pole odpowiedniego prostokąta pomnożone przez ilość takich prostokątów w siatce, czyli $P = 2 a b + 2 b c + 2 a c$ .

Ważne!

Wzór na pole powierzchni graniastosłupa:

P = 2 \cdot P_{p} + P_{b}

$P$ – pole powierzchni graniastosłupa,

$P_{p}$ – pole podstawy,

$P_{b}$ – pole powierzchni bocznej.

R1W6wIGUE2BjL1

Rysunek graniastosłupa prawidłowego trójkątnego oraz jego siatki. Siatka graniastosłupa składa się z dwóch trójkątów równobocznych o boku a oraz z trzech prostokątów o dłuższych bokach długości a i krótszych bokach długości w. Zapis: Pole powierzchni graniastosłupa prawidłowego trójkątnego o wysokości w i krawędzi podstawy a wynosi P =3 razy a razy w +2 razy ułamek, licznik a kwadrat razy pierwiastek z trzech mianownik 4. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pole powierzchni graniastosłupa prawidłowego trójkątnego o wysokości $w$ i krawędzi podstawy $a$

P = 3 a \cdot w + 2 \frac{a^{2} \sqrt{3}}{4}

RNuSCAsAWs78S1

Rysunek graniastosłupa prawidłowego sześciokątnego oraz jego siatki. Siatka graniastosłupa składa się z dwóch sześciokątów foremnych o boku długości a oraz z sześciu prostokątów o dłuższych bokach równych w i krótszych bokach równych a. Zapis: Pole powierzchni graniastosłupa prawidłowego sześciokątnego o wysokości w i krawędzi podstawy a wynosi P =6 razy a razy w +6 razy ułamek, licznik a kwadrat razy pierwiastek z trzech mianownik 4. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pole powierzchni graniastosłupa prawidłowego sześciokątnego o krawędzi podstawy $a$ i wysokości $w$

P = 6 a \cdot w + 3 a^{2} \sqrt{3}

Przykład 2

Podstawą graniastosłupa jest romb o wysokości $3 cm$ i kącie ostrym $30 °$ . Pole powierzchni bocznej jest równe $168 {cm}^{2}$ . Obliczymy wysokość graniastosłupa i jego pole powierzchni całkowitej.

RVcNyG5eXNk7z1

Rysunek dwóch figur. Pierwsza figura to graniastosłup prosty o podstawie rombu. Krawędź podstawy równa jest a i kąt ostry w rombie ma miarę 30 stopni. Wysokość bryły H. Druga figura to romb o wysokości 3 cm i boku równym a. Kąt ostry w tym rombie ma miarę 30 stopni. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Podstawą graniastosłupa jest romb, w którym kąt ostry ma miarę $30 °$ , a wysokość jest równa $3 cm$ . Z własności trójkąta prostokątnego o przyprostokątnej $3 cm$ i kącie ostrym leżącym naprzeciw tej przyprostokątnej o mierze $30 °$ wynika, że długość przeciwprostokątnej jest równa $6 cm$ .

Zatem bok rombu ma długość $6 cm$ .

Obliczymy wysokość $H$ graniastosłupa, korzystając z tego, że pole powierzchni bocznej jest równe $168 {cm}^{2}$ .

4 \cdot 6 \cdot H = 168

24 H = 168

H = 7 cm

Obliczamy pole podstaw graniastosłupa.

2 P_{p} = 2 \cdot 3 \cdot 6 = 36

2 P_{p} = 36 {cm}^{2}

Obliczamy pole powierzchni całkowitej graniastosłupa jako sumę pola podstaw i pola powierzchni bocznej.

P_{c} = 2 P_{p} + P_{b}

P_{c} = 36 + 168 = 204

P_{c} = 204 {cm}^{2}

Odpowiedź:

Wysokość graniastosłupa jest równa $7 cm$ , a pole powierzchni jest równe $204 {cm}^{2}$ .

Zadania

Ćwiczenie 1

R18GOIZNH0SLC1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rnm9OpLNB52wU

Dopasuj opisy do odpowiedniego pola powierzchni graniastosłupa prawidłowego o wysokości

5 cm

i opisanej podstawie. Trójkąt równoboczny o boku długości

2 dm

. Możliwe odpowiedzi: 1.

288 {cm}^{2}

, 2.

(200 \sqrt{3} + 300) {cm}^{2}

, 3.

(27 \sqrt{3} + 900) {mm}^{2}

Kwadrat o boku długości

8 cm

. Możliwe odpowiedzi: 1.

288 {cm}^{2}

, 2.

(200 \sqrt{3} + 300) {cm}^{2}

, 3.

(27 \sqrt{3} + 900) {mm}^{2}

Sześciokąt foremny o boku długości

3 mm

. Możliwe odpowiedzi: 1.

288 {cm}^{2}

, 2.

(200 \sqrt{3} + 300) {cm}^{2}

, 3.

(27 \sqrt{3} + 900) {mm}^{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 2

RDoBcAwLxLanO1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RXifd0acJOFpJ

Wysokość graniastosłupa jest równa

6, 5 dm

. Podstawami są wielokąty opisane poniżej. Dopasuj opisy do odpowiedniego pola powierzchni graniastosłupa. Równoległobok o podstawie długości

4 cm

i wysokości

6 cm

. Możliwe odpowiedzi: 1.

535 + 65 \sqrt{34} {cm}^{2}

, 2.

1348 {cm}^{2}

, 3.

(112 + (10 + 4 + 2 \sqrt{73}) \cdot 6, 5) {dm}^{2}

, 4.

1608 {c m}^{2}

Trójkąt prostokątny o przyprostokątnych długości

3 cm

5 cm

. Możliwe odpowiedzi: 1.

535 + 65 \sqrt{34} {cm}^{2}

, 2.

1348 {cm}^{2}

, 3.

(112 + (10 + 4 + 2 \sqrt{73}) \cdot 6, 5) {dm}^{2}

, 4.

1608 {c m}^{2}

Romb o przekątnych

8 cm

6 cm

. Możliwe odpowiedzi: 1.

535 + 65 \sqrt{34} {cm}^{2}

, 2.

1348 {cm}^{2}

, 3.

(112 + (10 + 4 + 2 \sqrt{73}) \cdot 6, 5) {dm}^{2}

, 4.

1608 {c m}^{2}

Trapez o podstawach długości

4 dm

10 dm

i wysokości

8 dm

. Możliwe odpowiedzi: 1.

535 + 65 \sqrt{34} {cm}^{2}

, 2.

1348 {cm}^{2}

, 3.

(112 + (10 + 4 + 2 \sqrt{73}) \cdot 6, 5) {dm}^{2}

, 4.

1608 {c m}^{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 3

R1SIMYoefvs0Y

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Suma pól podstaw to $60 - 48 = 12 ({cm}^{2})$ .

Ćwiczenie 4

RcqqLsqQoPnrb1

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 5

Krawędź podstawy graniastosłupa prawidłowego ma długość $4 cm$ . Wysokość graniastosłupa jest równa $6 cm$ . Narysuj siatkę tego graniastosłupa, wiedząc, że jego podstawą jest:

trójkąt
czworokąt
pięciokąt
sześciokąt

R1VqzXXyGA39r

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Krawędź podstawy graniastosłupa prawidłowego ma długość $4 cm$ . Wysokość graniastosłupa jest równa $6 cm$ . Opisz jak wygląda siatka tego graniastosłupa, wiedząc, że jego podstawą jest

trójkąt
czworokąt
pięciokąt
sześciokąt

R1T0eGwksrPUr

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY-SA 3.0.

RoI7BXPLKZpc7

R1CgQy4hp7T89

RwUGQDak9AdY3

R1TyvyGhDTmLr

Siastka graniastosłupa składa się z dwóch trójkątów równobocznych o bokach długości $4 cm$ i trzech prostokątów o wymiarach $4 cm \times 6 cm$ .
Siastka graniastosłupa składa się z dwóch kwadratów o bokach długości $4 cm$ i czterech prostokątów o wymiarach $4 cm \times 6 cm$ .
Siastka graniastosłupa składa się z dwóch pięciokątów foremnych o bokach długości $4 cm$ i pięciu prostokątów o wymiarach $4 cm \times 6 cm$ .
Siastka graniastosłupa składa się z dwóch sześciokątów foremnych o bokach długości $4 cm$ i sześciu prostokątów o wymiarach $4 cm \times 6 cm$ .

Ćwiczenie 6

R1LrkIoCqZw92

R1QEmhXymNFea

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RgJaHReBI9xWH

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 7

R1Wmpr0dQWYz8

Pudełko ma kształt graniastosłupa prostego, którego podstawą jest trójkąt prostokątny o przyprostokątnych długości

12 cm

16 cm

. Wysokość pudełka jest równa

10 cm

. Na kartce papieru narysowano siatkę tego pudełka w skali

1 : 4

. Oblicz, ile kartonu użyto do wykonania tego pudełka oraz jakie pole powierzchni ma narysowana na kartce siatka. Uzupełnij poniższe zdania, wpisując w luki odpowiednie liczby. Przeciwprostokątna podstawy ma długość Tu uzupełnij

cm

.Do wykonania tego pudełka użyto Tu uzupełnij

{cm}^{2}

kartonu.Pole narysowanej siatki wynosi Tu uzupełnij

{cm}^{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Do obliczenia długości przeciwprostokątnej podstawy wykorzystaj twierdzenie Pitagorasa. Aby obliczyć pole narysowanej siatki należy pole powierzchni całkowitej pudełka pomnożyć przez ułamek $\frac{1}{16}$ .

Przeciwprostokątna podstawy ma długość $\sqrt{12^{2} + 16^{2}} = \sqrt{400} = 20 (cm)$ .

Pole całkowite pudełka to $16 \cdot 12 + (16 + 12 + 20) \cdot 10 = 192 + 480 = 672 ({cm}^{2})$ .

Pole narysowanej siatki to $\frac{1}{16} \cdot 672 = 42 ({cm}^{2})$ .

Ćwiczenie 8

RQ1Z9I3AbzmSn

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Rzg0tZDj0lscS

Ćwiczenie 9

Rysunek przedstawia siatkę graniastosłupa. Rozstrzygnij, czy zdanie jest prawdziwe, czy fałszywe.

Rg8jS4RerSGho1

Rysunek siatki graniastosłupa złożonej z dwóch foremnych sześciokątów o boku równym 3 cm i sześciu prostokątów o bokach 3 cm i 5 cm. Wszystkie prostokąty tworzące ściany boczne ułożone są w jednej linii i mają wspólne dłuższe krawędzie. Jeden z sześciokątów jest styczny do górnej krawędzi drugiego prostokąta, a drugi sześciokąt jest styczny do dolnej krawędzi szóstego prostokąta. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

R1Ioia1gzxt7D

Suma długości krawędzi graniastosłupa jest o $30 cm$ większa od sumy długości krawędzi bocznych.
Pole powierzchni podstawy jest równe $13,5 \sqrt{3} c m^{2}$ .
Pole powierzchni całkowitej jest o $75 c m^{2}$ większe od sumy pól powierzchni podstaw.
Krawędź boczna graniastosłupa jest nachylona do podstawy pod kątem $72 °$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Suma długości krawędzi bocznych to $6 \cdot 5 = 30 (cm)$ , suma wszystkich krawędzi to $6 \cdot 3 \cdot 2 + 30 = 66 (cm)$ , czyli jest o $36 cm$ większa. Zdanie prawdziwe.
Pole podstawy to $6 \cdot \frac{3^{2} \sqrt{3}}{4} = 13, 5 \sqrt{3} ({cm}^{2})$ . Zdanie to jest więc prawdziwe.
Suma pól podstaw jest równa $27 \sqrt{3} {cm}^{2}$ , zaś pole powierzchni całkowitej to $6 \cdot 3 \cdot 5 + 27 \sqrt{3} = 90 + 36 \sqrt{3} ({cm}^{2})$ . Zdanie jest fałszywe.
Krawędź boczna jest prostopadłą, więc jest to zdanie fałszywe.

Ćwiczenie 10

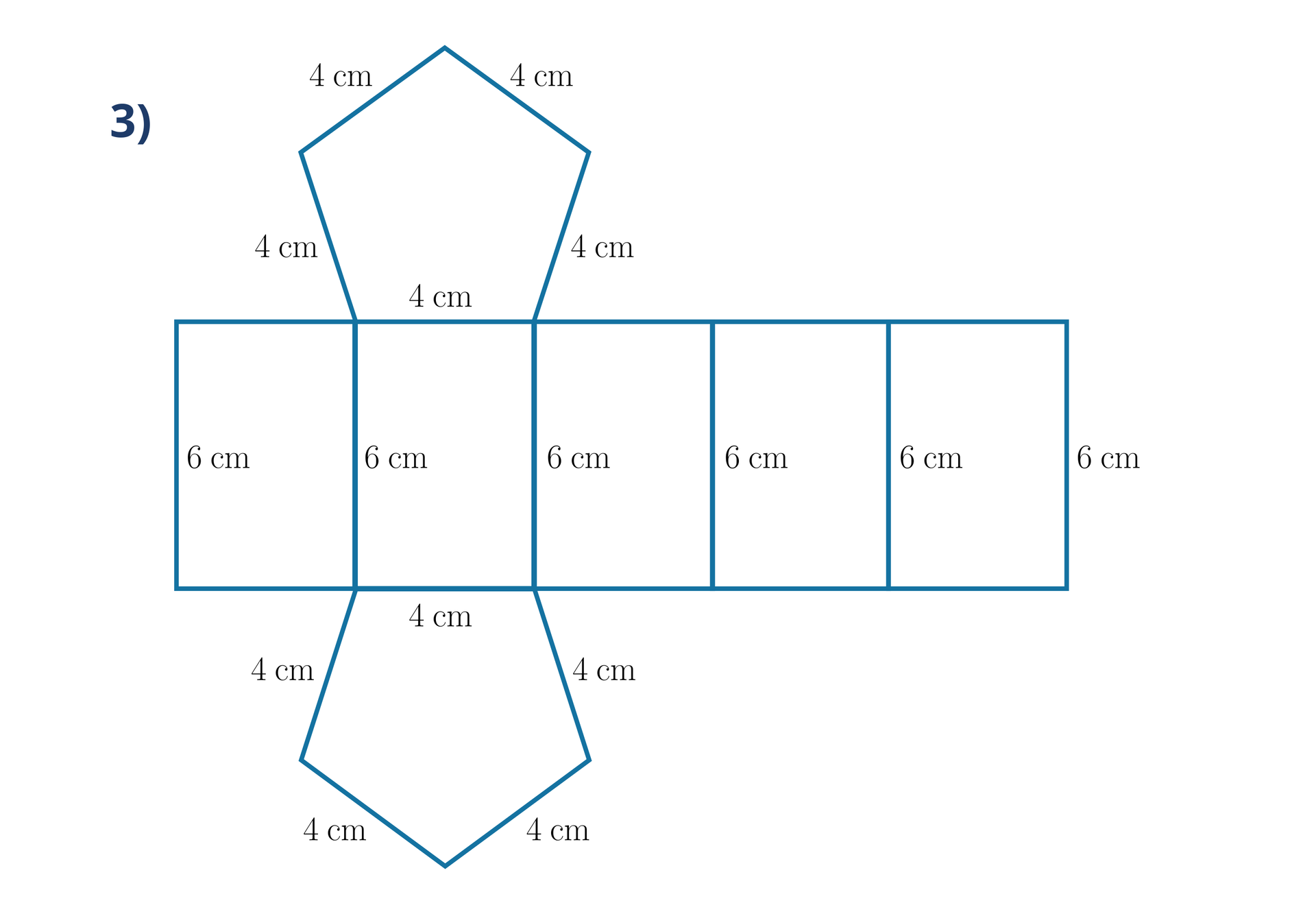
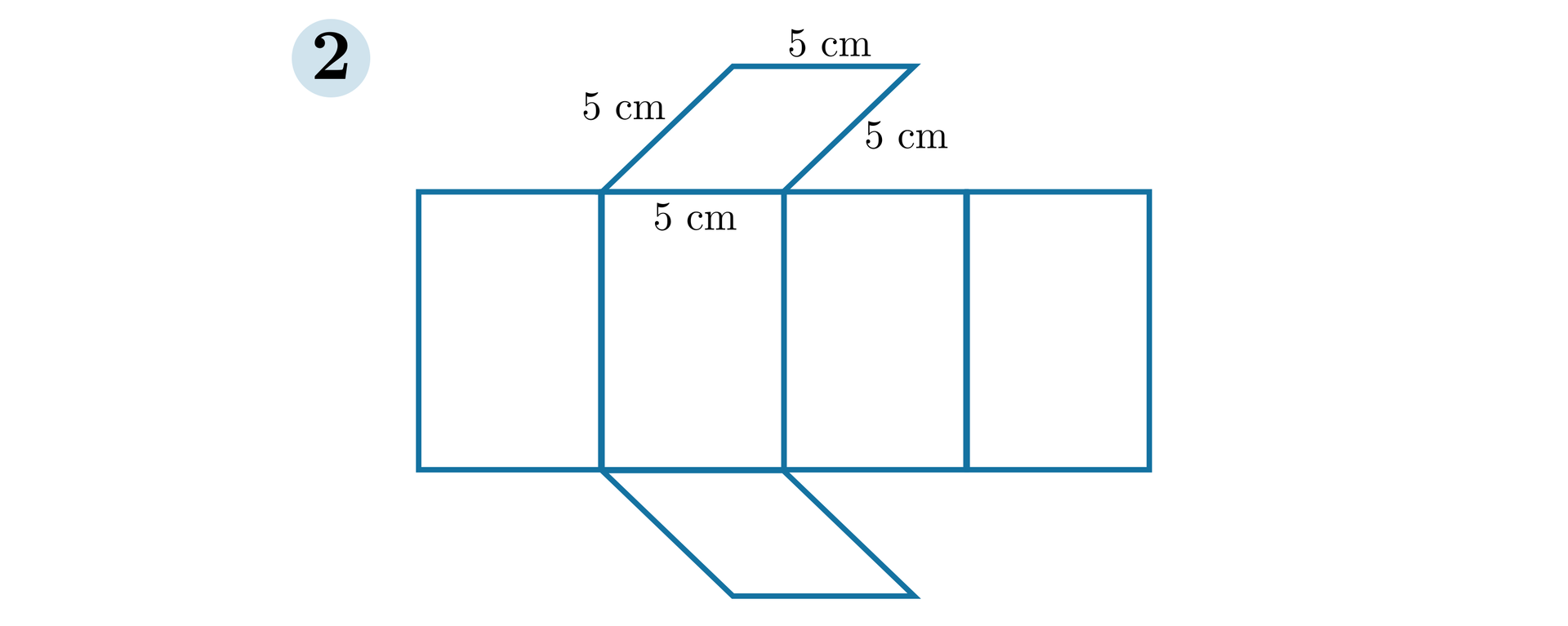
Siatki graniastosłupów prostych przedstawionych na poniższych ilustracjach składają się z odcinków, których suma długości jest równa $100 cm$ . Oblicz, jakie są długości wysokości tych graniastosłupów.

RbhgrRRKsdSL8

Ilustracja przedstawia pierwszą siatkę. Jest to siatka graniastosłupa prawidłowego trójkątnego. W podstawie tego graniastosłupa znajduje się trójkąt prostokątny o przeciwprostokątnej długości 10 cm i przyprostokątnej długości 6 cm. Siatka jest zbudowana w taki sposób, że jedna podstawa ma wszystkie boki wspólne ze ścianami bocznymi, a druga podstawa ma tylko jeden wspólny bok ze ścianą boczną - dłuższą przyprostokątną. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RQr0weaX7jM0N

Ilustracja przedstawia drugą siatkę. Jest to siatka graniastosłupa prawidłowego czworokątnego. W podstawie tego graniastosłupa znajduje się romb o długości boku 5 cm. Siatka jest zbudowana w taki sposób, że każda podstawa ma tylko jeden wspólny bok ze ścianą boczną. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RYrH5ESP1lnM7

Ilustracja przedstawia trzecią siatkę. Jest to siatka graniastosłupa prawidłowego pięciokątnego. W podstawie tego graniastosłupa znajduje się pięciokąt foremny o długości boku 5 cm. Siatka jest zbudowana w taki sposób, że pierwsza podstawa ma wszystkie boki wspólne ze ścianami bocznymi, a druga podstawa ma tylko jeden bok wspólny ze ścianą boczną. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RrEVLMhbjO9az2

Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Wysokość graniastosłupa zbudowanego z pierwszej siatki wynosi 1.

3

, 2.

6

, 3.

4

, 4.

6

, 5.

5

, 6.

4

cm

.Wysokość graniastosłupa zbudowanego z drugiej siatki wynosi 1.

3

, 2.

6

, 3.

4

, 4.

6

, 5.

5

, 6.

4

cm

.Wysokość graniastosłupa zbudowanego z trzeciej siatki wynosi 1.

3

, 2.

6

, 3.

4

, 4.

6

, 5.

5

, 6.

4

cm

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 11

R6KVjjMQzpnqZ

Uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Dany jest graniastosłup, którego podstawą jest trójkąt, w którym dwa kąty mają miary

30 °

60 °

, a najdłuższy bok ma długość

10 cm

. Wysokość tego graniastosłupa jest równa

1, 5 dm

. Pole powierzchni bocznej tego graniastosłupa wynosi 1.

75 \sqrt{3} + 225

, 2.

20

, 3.

55 \sqrt{2} + 25

, 4.

36, 8

, 5.

125 \sqrt{3} + 25

, 6.

55 \sqrt{3} + 22

, 7.

27

, 8.

25, 5

, 9.

35, 2

, 10.

25 \sqrt{5} + 125

, 11.

36, 6

{cm}^{2}

.

Dany jest graniastosłup, którego podstawą jest trapez prostokątny o wysokości

4 cm

i podstawach długości

5 cm

8 cm

. Wysokość tego graniastosłupa stanowi

20 %

najdłuższego boku trapezu. Pole powierzchni bocznej tego graniastosłupa wynosi 1.

75 \sqrt{3} + 225

, 2.

20

, 3.

55 \sqrt{2} + 25

, 4.

36, 8

, 5.

125 \sqrt{3} + 25

, 6.

55 \sqrt{3} + 22

, 7.

27

, 8.

25, 5

, 9.

35, 2

, 10.

25 \sqrt{5} + 125

, 11.

36, 6

{cm}^{2}

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Przeciwprostokątna trójkąta w podstawie ma długość $10 cm$ , a krótsza przyprostokątna – $5 cm$ . Stąd druga przyprostokątna ma długość $5 \sqrt{3} cm$ . Pole powierzchni bocznej jest równe:
$(5 \sqrt{3} + 10 + 5) \cdot 15 = (75 \sqrt{3} + 225) ({cm}^{2})$ .
Długości boków trapezu są równe $4 cm$ , $8 cm$ , $5 cm$ i $5 cm$ . Wysokość graniastosłupa jest równa

0, 2 \cdot 8 cm = 1, 6 cm

Pole boczne graniastosłupa to $(4 + 8 + 5 + 5) \cdot 1, 6 = 35, 2 ({cm}^{2})$ .

Ćwiczenie 12

RXb3Y0ajoWXJH

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wysokość trapezu jest równa $1 cm$ , pole trapezu jest równe $9 {cm}^{2}$ . Pole powierzchni całkowitej jest równe

18 + (8 + 10 + 2 \sqrt{2}) \cdot h

Zatem otrzymujemy równanie

18 + (18 + 2 \sqrt{2}) \cdot h = 24 (6 + \sqrt{2})

Stąd

h = \frac{543 + 45 \sqrt{2}}{79} cm

R1WOGndBl95Cm2

Ćwiczenie 13

pole podstawy graniastosłupa jest większe od $20$ .
pole powierzchni bocznej jest równe $120$ .
pole powierzchni całkowitej jest równe $84$ .
pole podstawy jest mniejsze od pola powierzchni bocznej o $20$ .

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 14

R1FI2xDwXizak

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pole podstawy to $\frac{6 \cdot 8}{2} = 24 {cm}^{2}$ . Długość krawędzi podstawy – $5 cm$ .

Pole powierzchni bocznej jest równe $20 \cdot 10 = 200 ({cm}^{2})$ .

RiYPYJT4lNOi52

Ćwiczenie 15

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 16

RUu9X5JOjpgW2

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Krawędź boczna to połowa przekątnej, czyli $2 \sqrt{10}$ . Długość krawędzi podstawy $x$ spełnia równanie

x^{2} = {(4 \sqrt{10})}^{2} - {(2 \sqrt{10})}^{2} = 120

skąd $x = 2 \sqrt{30}$ .

Pole powierzchni bocznej jest równe

(5 \cdot 2 \sqrt{30}) \cdot 2 \sqrt{10} = 20 \sqrt{300} = 200 \sqrt{3}

Ćwiczenie 17

RSVjvFa2oLdDI

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Wysokość podstawy jest równa $4 cm$ , pole podstawy to $12 {cm}^{2}$ , wysokość graniastosłupa to $6 cm$ .

Ćwiczenie 18

R1Qe2Kt4S1Cqz

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Długość krawędzi podstawy jest równa wysokości graniastosłupa i wynosi $4 \sqrt{2}$ .

Pole podstawy jest równe $6 \frac{{(4 \sqrt{2})}^{2} \cdot \sqrt{3}}{4} = 48 \sqrt{3}$ . Pole powierzchni całkowitej jest równe:

$2 \cdot 48 \sqrt{3} + 6 {(4 \sqrt{2})}^{2} = 96 \sqrt{3} + 192 = 96 (\sqrt{3} + 2)$ .

Ćwiczenie 19

R1amhyZGuP1pi

Suma długości wszystkich krawędzi każdego z dwóch graniastosłupów prawidłowych: trójkątnego oraz czworokątnego jest równa

36 cm

. Wszystkie krawędzie mają jednakową długość. Który z tych graniastosłupów ma większe pole powierzchni całkowitej? Uzupełnij odpowiedź, przeciągając w lukę odpowiednie słowo lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. Odpowiedź: Pole powierzchni graniastosłupa 1. trójkątnego, 2. czworokątnego jest większe.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Graniastosłup trójkątny ma $9$ krawędzi, czyli każda ma $4 cm$ długości.

W prostopadłościanie jest ich $12$ , więc każda ma $3 cm$ długości. Pole powierzchni całkowitej graniastosłupa trójkątnego to

2 \frac{16 \sqrt{3}}{4} + 3 \cdot 16 = 8 \sqrt{3} + 48 \approx 61, 85 ({cm}^{2})

pole powierzchni prostopadłościanu jest równe $54 {cm}^{2}$ .

Ćwiczenie 20

Betonowy blok ma kształt sześcianu o krawędzi długości $50 cm$ . W bloku wycięto otwór, tak jak na rysunku. Otwór ma kształt prostopadłościanu, którego niektóre krawędzie mają długość $10 cm$ . Oblicz pole powierzchni pozostałej części bloku.

R1eeYzsdkEsAi1

Rysunek betonowego bloczku w kształcie sześcianu z wyciętym w środku otworem w postaci prostopadłościanu. — Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

RGMdXhFVC8Ue8

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Pole pozostałej części jest równe $4 \cdot 50^{2} + 4 \cdot 50 \cdot 10 + 2 \cdot (50^{2} - 10^{2}) = 16800 ({cm}^{2})$ .

Ćwiczenie 21

RnawsIxGQupnS

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

ReX17UmgnE1Nl3

Ćwiczenie 22

Pola powierzchni dwóch sześcianów są równe. Wynika z tego, że ich krawędzie też są równe.
Jeśli krawędzie jednego graniastosłupa są odpowiednio równe krawędziom drugiego graniastosłupa, to graniastosłupy te mają jednakowe pola powierzchni.
Jeśli wszystkie krawędzie prostopadłościanu zwiększymy dwukrotnie, to jego powierzchnia całkowita zwiększy się czterokrotnie.

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Ćwiczenie 23

Oceń prawdziwość poniższego wniosku.

Krawędź podstawy graniastosłupa prawidłowego trójkątnego ma długość $10$ .

Wysokość graniastosłupa jest równa $0, 5$ . Zatem pole jego powierzchni całkowitej wyraża się liczbą naturalną.

RhKC4dIDs3pwI

Źródło: Zespół autorski Politechniki Łódzkiej, licencja: CC BY 3.0.

Fałsz. Ponieważ wysokość trójkąta będącego podstawą jest równa $\sqrt{3}$ , więc liczba wyrażająca pole powierzchni całkowitej nie będzie liczbą naturalną.