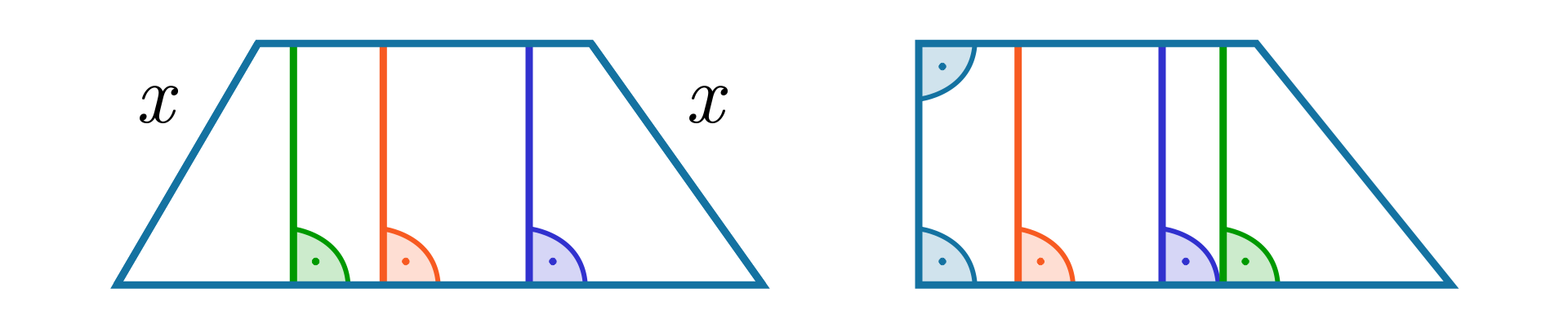Pole trapezu
W tym materiale przypomnisz sobie podstawowe informacje na temat trapezów oraz ich pól powierzchni. Zawarte są w nim podstawowe definicje oraz własności związane z różnymi trapezami.
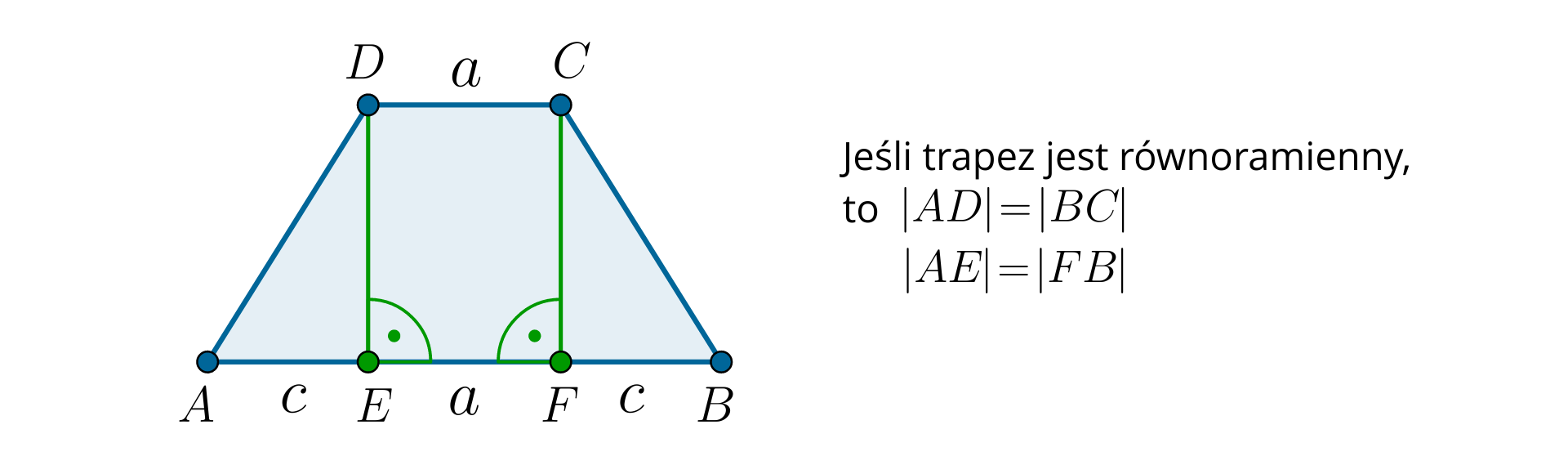
W tym materiale mówimy o trapezach, które nie są równoległobokami.
Wysokość trapezu
Film dostępny pod adresem /preview/resource/RYW6d3OBch2zv
Animacja przedstawia które odcinki możemy nazywać wysokościami trapezu.
Narysuj dowolny trapez równoramienny i dowolny trapez prostokątny. W każdym z nich narysuj kilka odcinków prostopadłych do obu podstaw, tak by połączyły podstawy.
Wyobraź sobie dowolny trapez równoramienny i dowolny trapez prostokątny. W każdym z nich możemy wyznaczyć odcinek prostopadły do obu podstaw, tak by połączył podstawy. Ile takich odcinków możemy wyznaczyć? Jakie długości będą miały wyznaczone odcinki?
Odcinek, który łączy obie podstawy trapezu i jest prostopadły do nich, nazywamy wysokością trapezu.
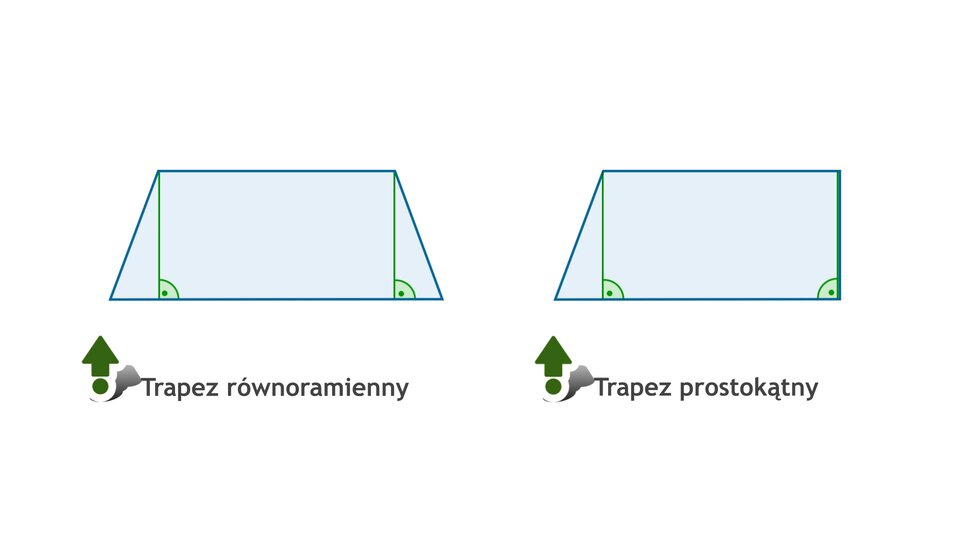
Trapez ma jedną wysokość. Można ją narysować w różnych miejscach. Wysokość trapezu to odcinek, który musi być prostopadły do podstaw i łączy podstawy lub ich przedłużenia.
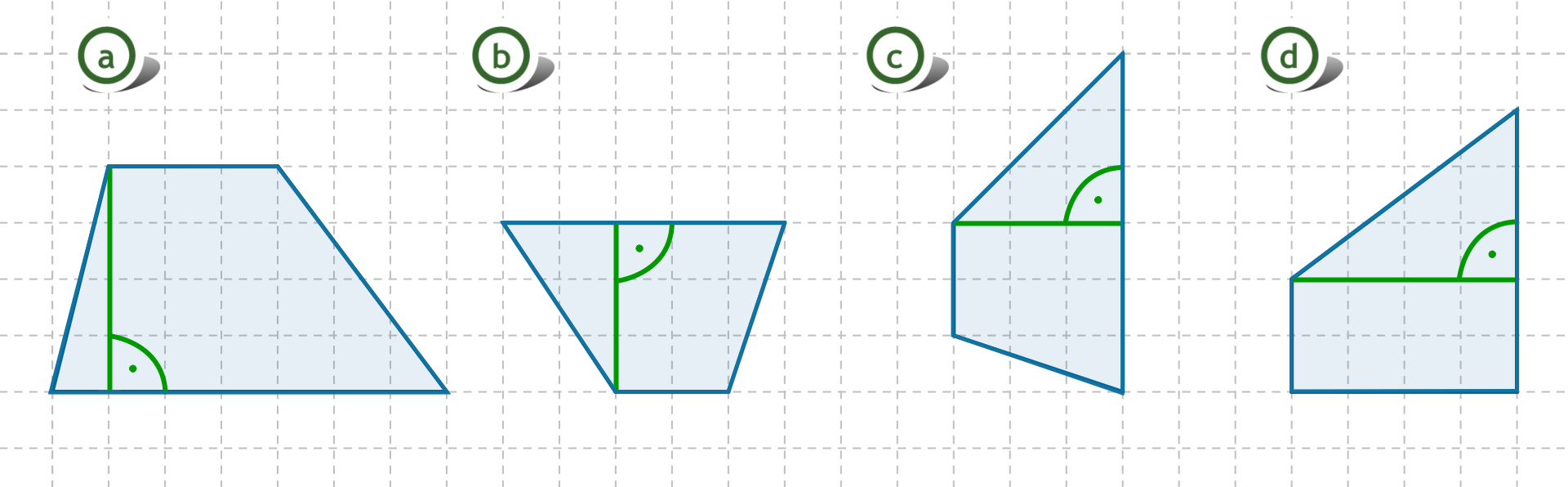
Narysuj wysokości poniższych trapezów.
Zastanów się, które boki poniższych trapezów połączy jego wysokość.

Pole trapezu – wzór
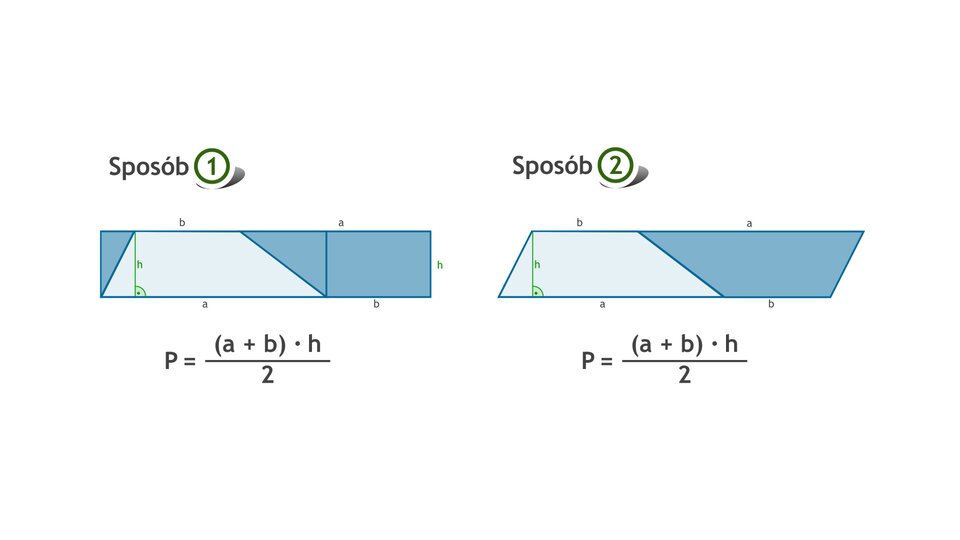
Film dostępny pod adresem /preview/resource/R1SF9FSW83e1x
Animacja przedstawia i uzasadnia wzór na pole powierzchni trapezu.
Pole trapezu jest połową iloczynu sumy długości jego podstaw oraz wysokości.

Obliczanie pola trapezu
Oblicz pole trapezu równoramiennego przedstawionego na rysunku.

Pole trapezu – zadania
Oblicz pola figur. Przyjmij, że bok kratki ma długość .

Znając pole trapezu oraz długość jego wysokości i jednej z podstaw, możemy wyznaczyć długość drugiej podstawy.
Pole trapezu jest równe , jego wysokość ma długość , a jedna z podstaw . Obliczmy długość drugiej podstawy.
Wiemy, że , więc sposób obliczenia pola tego trapezu można przedstawić za pomocą następującego grafu:

Jeśli wykonamy działania odwrotne, to obliczymy długość podstawy .

Obliczenia te można zapisać także bez grafu.
Obliczyliśmy więc, że druga podstawa trapezu ma długość .
Oblicz długość drugiej podstawy trapezu, a następnie uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Druga podstawa trapezu ma długość 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .
Oblicz długość wysokości trapezu, a następnie uzupełnij równości, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 1. , 2. , 3. , 4. , 5. , 6. 1. , 2. , 3. , 4. , 5. , 6. 1. , 2. , 3. , 4. , 5. , 6. 1. , 2. , 3. , 4. , 5. , 6.
Wysokość trapezu ma długość 1. , 2. , 3. , 4. , 5. , 6. .
Oblicz długość drugiej podstawy trapezu, a następnie uzupełnij zdania, przeciągając w luki odpowiednie liczby lub kliknij w lukę i wybierz odpowiedź z listy rozwijalnej. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8.
Druga podstawa trapezu ma długość 1. , 2. , 3. , 4. , 5. , 6. , 7. , 8. .