Pole wielokąta
W tym materiale poznasz definicje wielokątów wypukłych i wklęsłych. Dowiesz się jak obliczać pola różnych wielokątów, w tym także wielokątów foremnych. Rozwiążesz zadania dotyczące tych zagadnień.
Film dostępny pod adresem /preview/resource/RHk6Oyen3s9OF
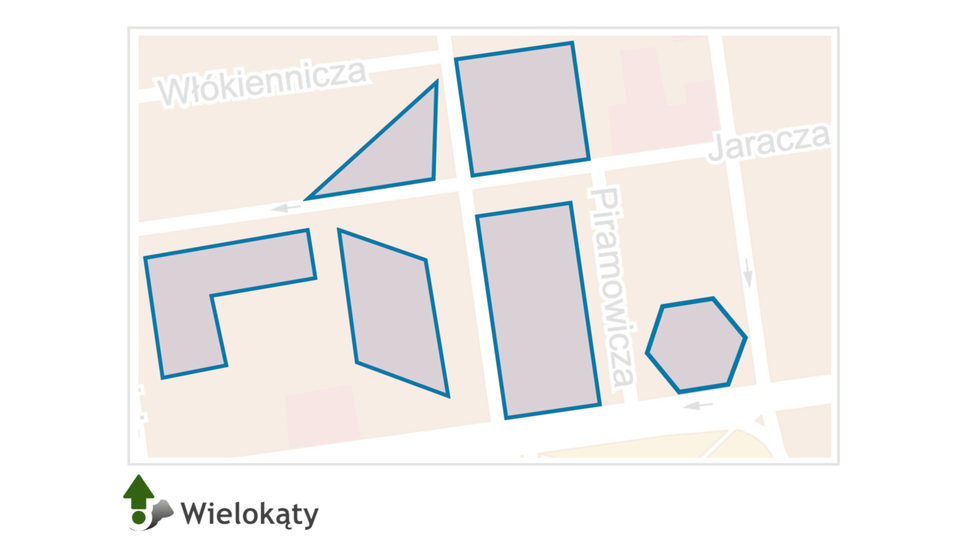
Animacja pokazuje różne rodzaje wielokątów na przykładzie planu miasta.
Wielokąty wypukłe i wklęsłe
Wielokąt jest wklęsły, jeżeli co najmniej jeden z jego kątów ma miarę większą od . Wielokąt, który nie jest wklęsły, to wielokąt wypukły.
Rysunek przedstawia kilka wielokątów wypukłych, a rysunek kilka wielokątów wklęsłych. Możemy zauważyć, że na rysunku odcinki łączące wybrane punkty w wielokącie są w nim zawarte, a na rysunku istnieją odcinki łączące punkty w wielokącie, które częściowo leżą poza tym wielokątem.

Jeżeli odcinek łączący dwa dowolne punkty w wielokącie jest całkowicie w nim zawarty, to taki wielokąt nazywamy wypukłym.
Trapezoid to czworokąt, w którym nie ma żadnej pary boków równoległych. Czworokąty wypukłe to trapezy albo trapezoidy.
Obliczanie pól wielokątów
Wiemy już, że każdy wielokąt, zarówno wypukły, jak i wklęsły, można podzielić na skończoną liczbę trójkątów. Pole wielokąta jest równe sumie pól trójkątów. Jednak nie zawsze łatwe jest wyznaczenie tych pól. W praktyce dzielimy więc wielokąt na takie figury, których pola łatwo wyznaczyć, przy tym staramy się, aby tych figur było jak najmniej.

Pokażemy, w jaki sposób obliczyć pole wielokąta , gdzie , , , , , , ?
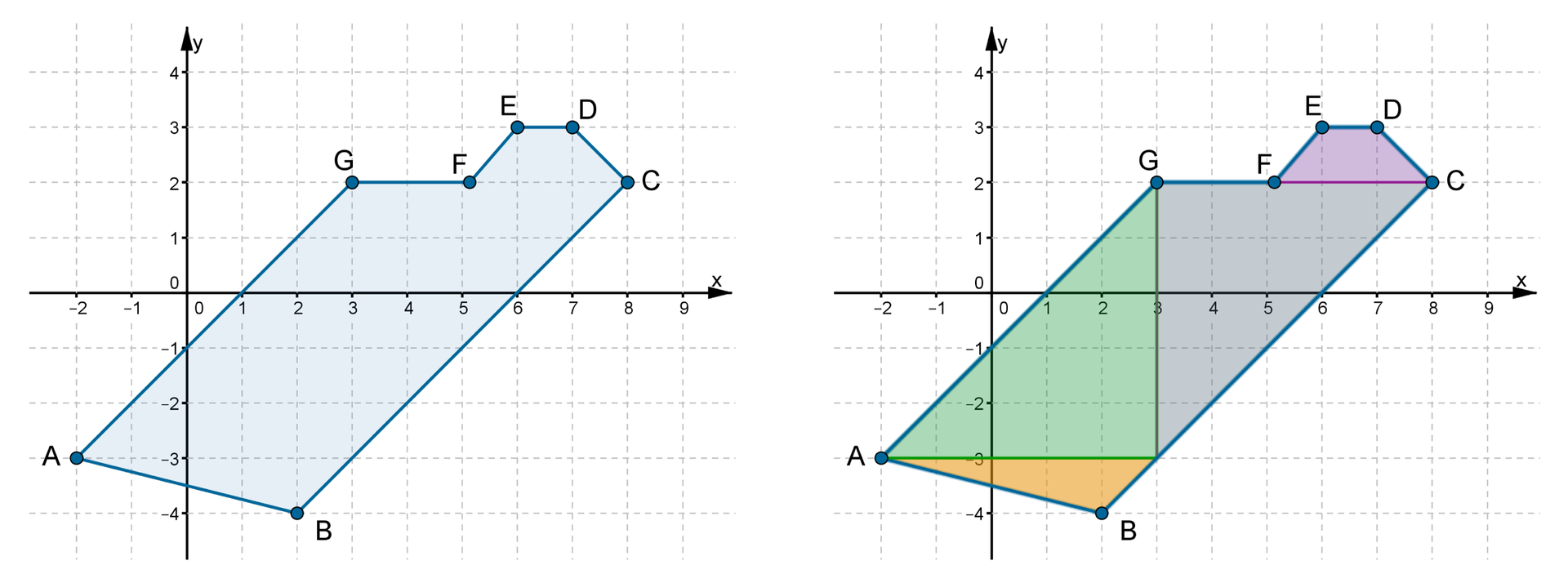
Zaznaczamy wielokąt w układzie współrzędnych. Następnie dzielimy go na trapez oraz trójkąty i obliczamy pola tych figur.
Pole sześciokąta foremnego
Pole sześciokąta foremnego o boku długości jest równe
Sześciokąt foremny, którego bok ma długość , można podzielić na przystających trójkątów równobocznych. Długość boku takiego trójkąta jest równa , zatem jego pole to .

Pole sześciokąta foremnego jest sześciokrotnie większe od pola trójkąta, zatem
Obliczymy obwód sześciokąta foremnego o polu .
Obliczamy długość boku sześciokąta.
bo .
Obliczamy obwód sześciokąta.
Obwód sześciokąta jest równy .
Obliczymy długość krótszej przekątnej sześciokąta foremnego o boku długości .
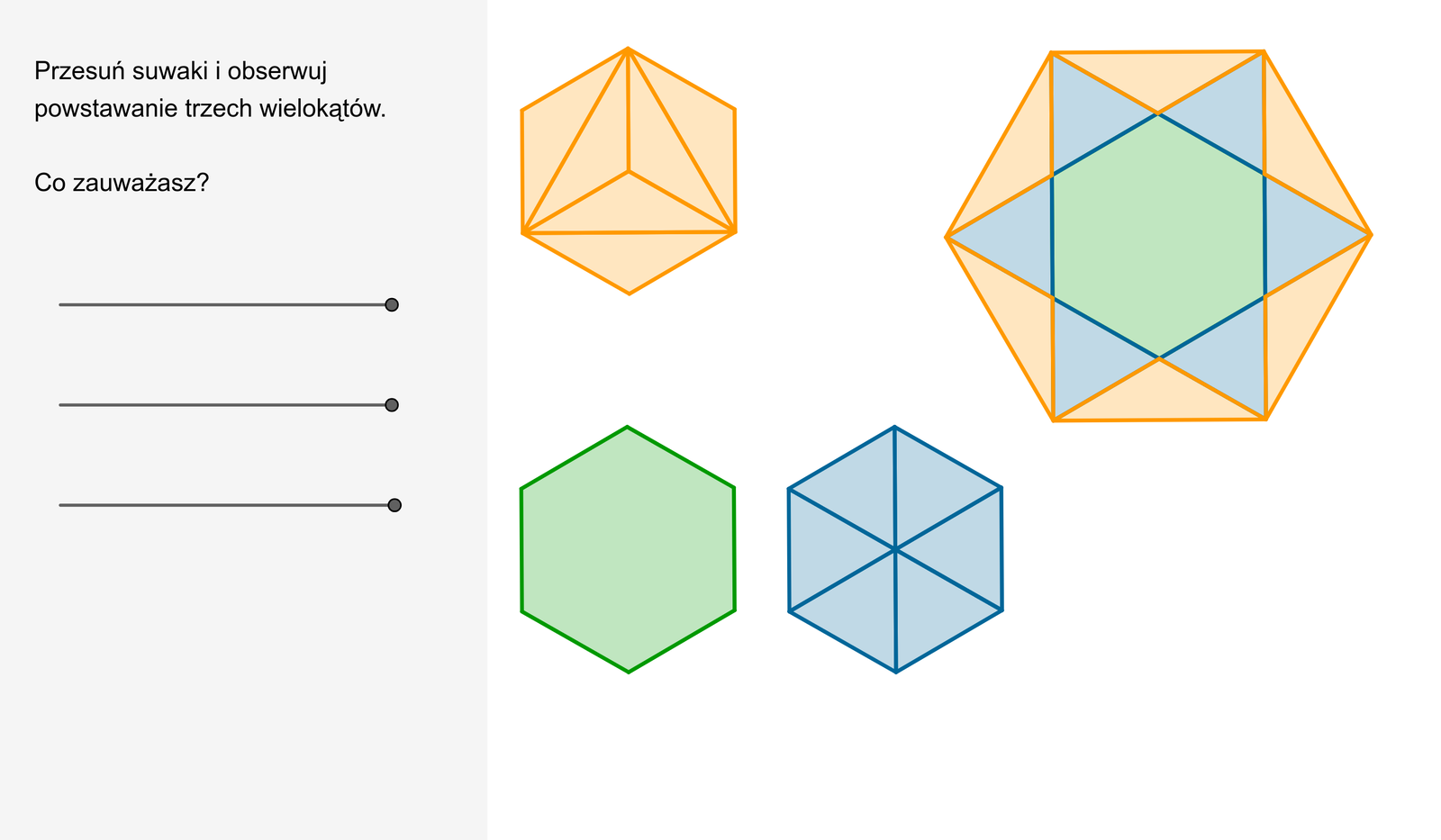
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P3AYyv4qJ
Sześciokąt można podzielić na trzy przystające sześciokąty foremne.
Obliczamy długość boku każdego z mniejszych sześciokątów.
bo i
Krótsza przekątna sześciokąta jest razy dłuższa od .

Krótsza przekątna sześciokąta foremnego o boku długości jest równa .
Pole deltoidu
Deltoid jest czworokątem, którego przekątne są prostopadłe i jedna z nich jest zawarta w osi symetrii deltoidu.
Wykażemy, że pole deltoidu można obliczyć podobnie jak pole rombu.
Rozważmy deltoid o przekątnych długości i .

Zauważmy, że deltoid można przekształcić w prostokąt o bokach długości i .
Pole tego prostokąta, jak również pole deltoidu, jest równe .
Pole deltoidu o przekątnych długości i jest równe
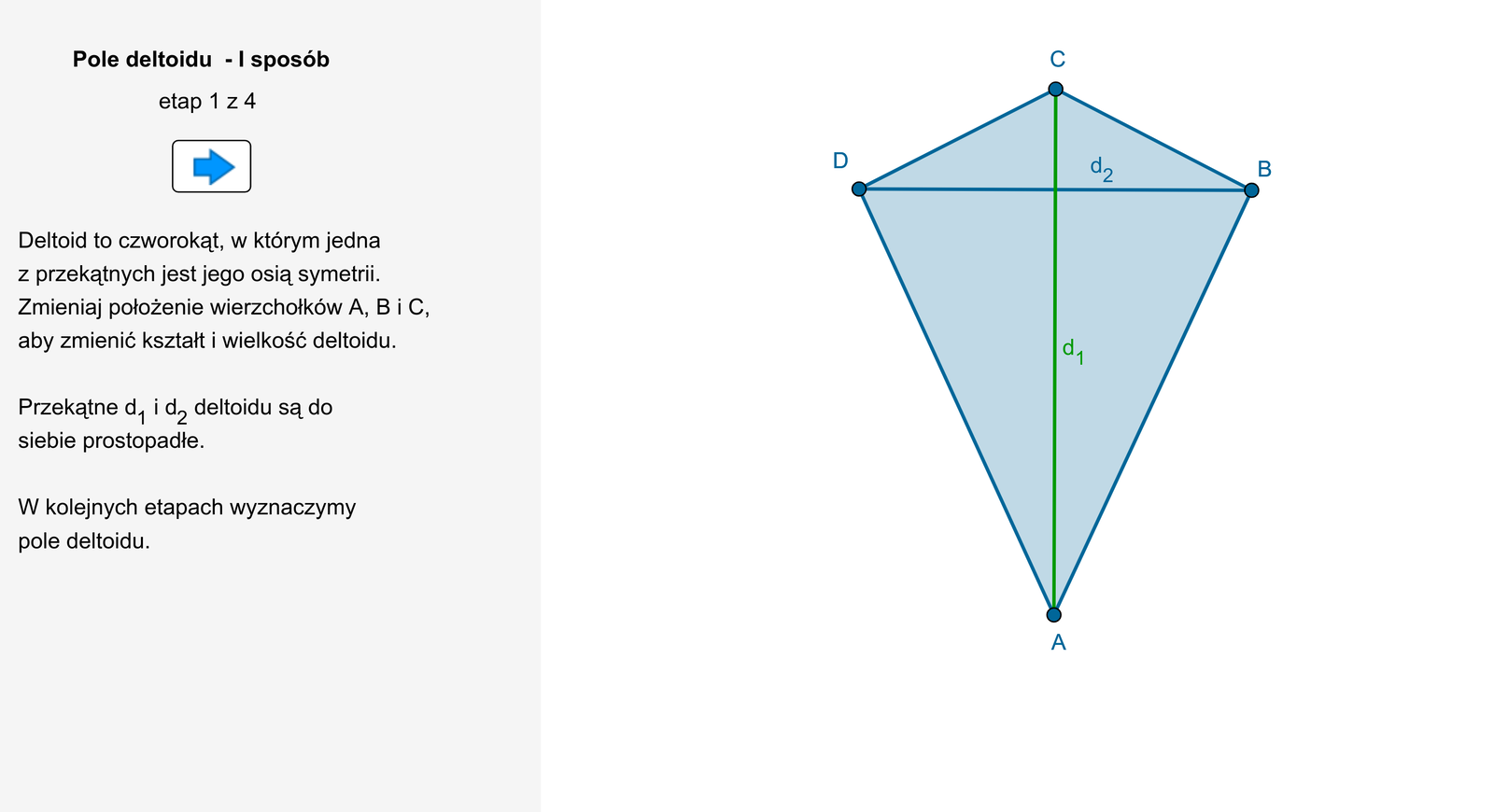
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P3AYyv4qJ
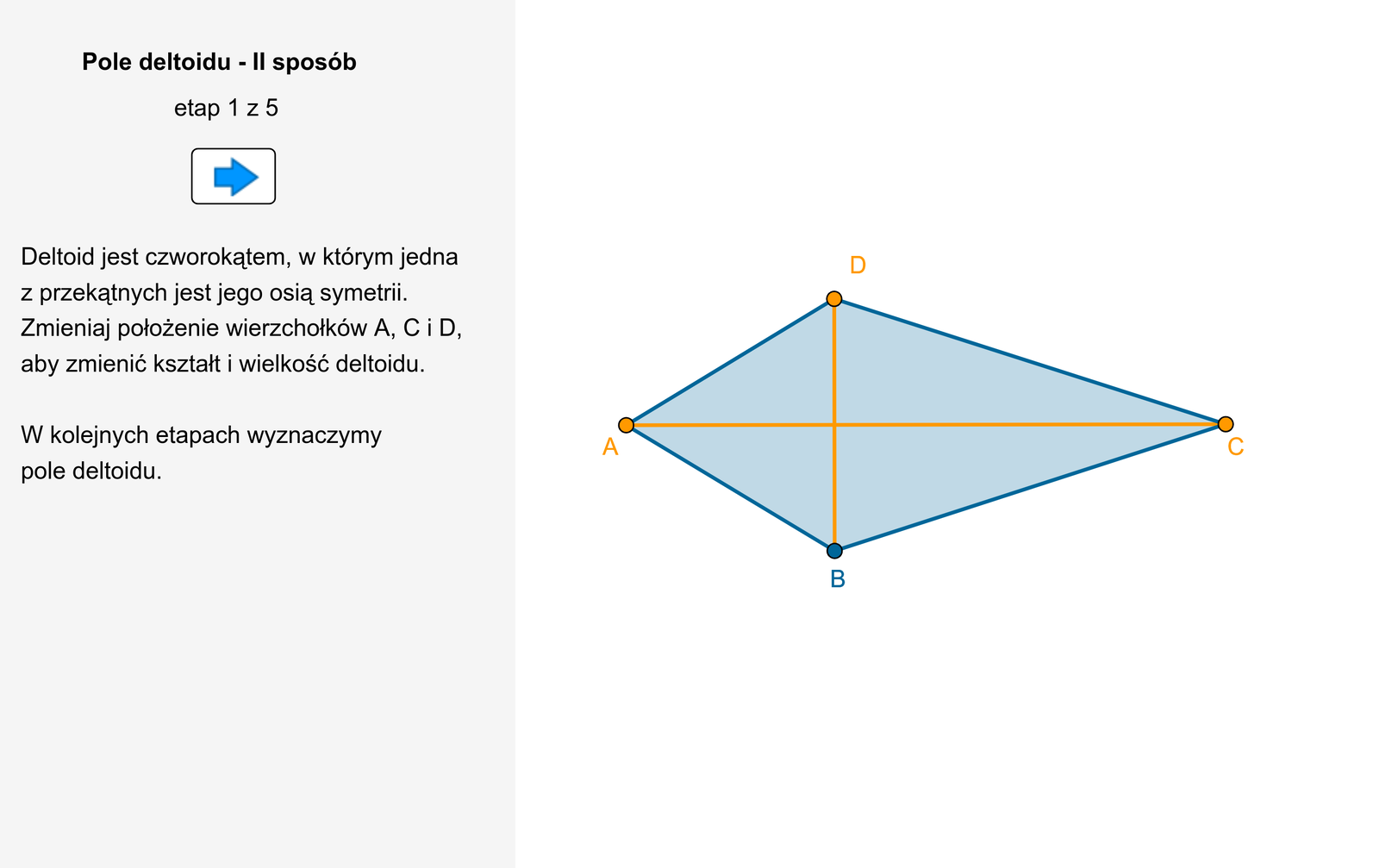
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P3AYyv4qJ
Krótsza przekątna dzieli deltoid na trójkąt równoboczny o polu i trójkąt równoramienny o ramieniu długości . Obliczymy pole deltoidu.

Oznaczmy wierzchołki deltoidu , , , . Trójkąt jest równoboczny i jego pole jest równe .
Obliczamy długość boku tego trójkąta.
Stąd
Z trójkąta prostokątnego , korzystając z twierdzenia Pitagorasa, wyznaczamy długość boku .
Obliczamy pole deltoidu jako sumę pól trójkątów i .
Pole deltoidu jest równe .
Twierdzenie Picka
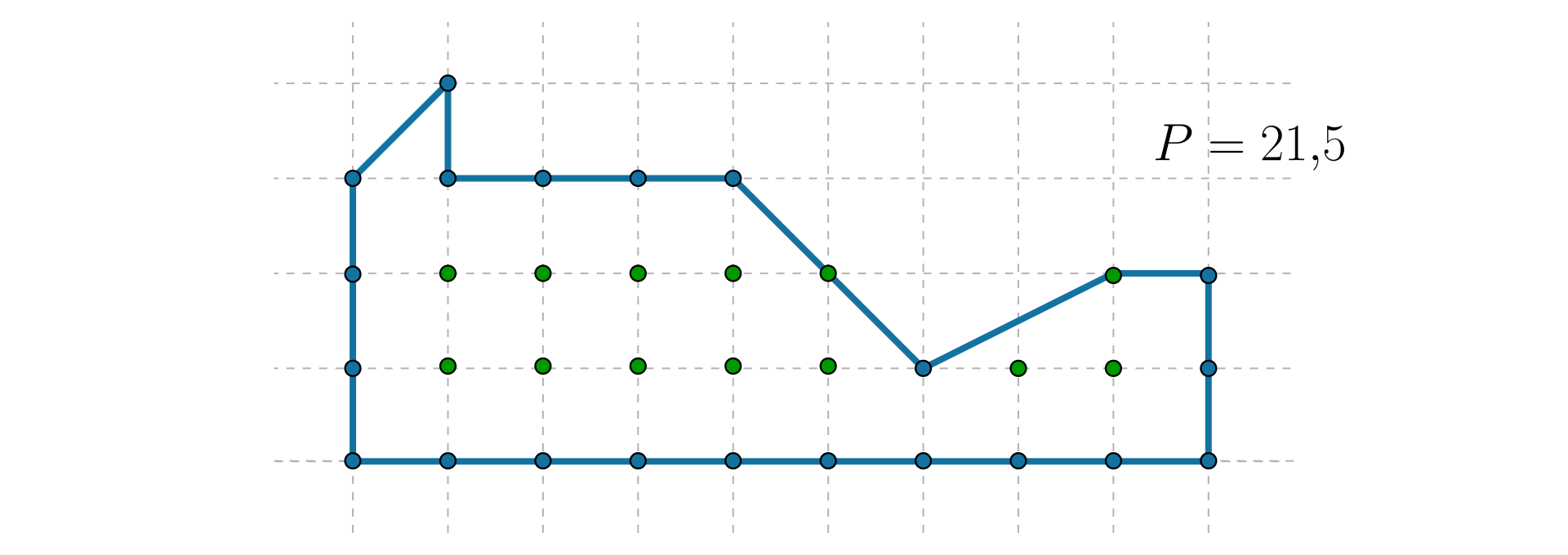
Matematyk Aleksander George Pick , pracujący na uniwersytetach w Wiedniu, Pradze i Dreźnie, odkrył metodę, która pozwala na obliczenie pola wielokąta, którego wierzchołki są punktami kratowymi (czyli leżą na przecięciu linii tworzących kratki) bez wykorzystania znanych nam wzorów i bez podziału wielokąta na trójkąty (lub inne wielokąty).
Zauważył on, że pole takich wielokątów zależy tylko od liczby punktów kratowych, które leżą wewnątrz i na brzegu wielokąta.
Na rysunku przedstawione są trzy wielokąty, których pola są równe. Punkty kratowe leżące na brzegach wielokątów zaznaczone są kolorem niebieskim, a we wnętrzu – żółtym. Zmieniaj położenie wierzchołków wielokąta. Obliczaj w każdym przypadku pole wielokąta i porównuj otrzymany przez Ciebie wynik z wynikiem zapisanym na ekranie.
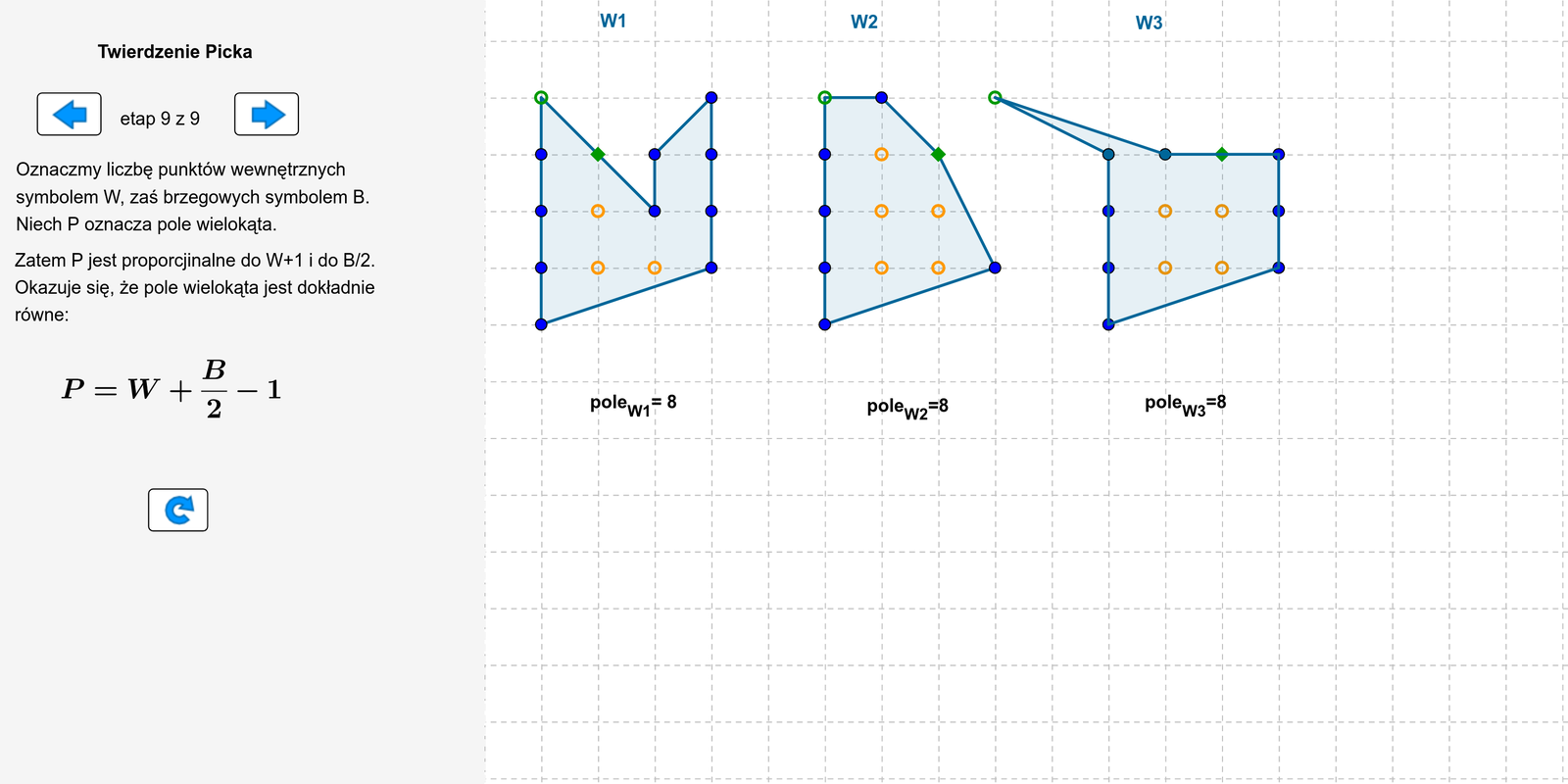
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/b/P3AYyv4qJ
Wyznacz pole wielokąta, korzystając ze wzoru Picka.

Bronek nie dokończył rysunku wielokąta . Dokończ rysunek, wiedząc, że pole wielokąta jest równe , a każdy z brakujących wierzchołków leży w jednym z punktów zaznaczonych na rysunku.

Bronek narysował wielokąt . Pole tego wielokąta jest równe , a wewnątrz niego znajduje się punktów kratowych. Ile punktów kratowych leży na brzegu tego wielokąta?
- Pięciokąt foremny może mieć pole równe polu sześciokąta foremnego.
- Z każdych czterech odcinków można zbudować czworokąt.
- Wielokąt wklęsły nie ma przekątnych.
- Istnieje wielokąt, który nie ma przekątnych.
- Niektóre deltoidy są kwadratami.
- Każdy prostokąt jest trapezem.
- Każdy bok wielokąta musi mieć długość mniejszą niż suma długości boków pozostałych.
- Jeżeli czworokąt jest wypukły, to obie jego przekątne leżą wewnątrz tego czworokąta.
- Jeżeli czworokąt jest wklęsły, to jedna jego przekątna leży wewnątrz tego czworokąta, a druga leży poza czworokątem.
- Czworokąt foremny jest kwadratem.
Udowodnij, że jeśli przekątne czworokąta są prostopadłe, to niezależnie od jego kształtu pole czworokąta jest równe połowie iloczynu długości przekątnych.
Uporządkuj rosnąco liczby , , , gdzie jest polem sześciokąta, którego bok ma długość . jest polem rombu, którego przekątna ma długość , a bok ma długość . Natomiast jest polem deltoidu o przekątnych długości .
Oszacuj, ile szkła potrzeba na wykonanie dwóch witraży, z których jeden ma kształt sześciokąta foremnego o boku długości , a drugi deltoidu o przekątnych długości .
Punkt jest punktem wewnętrznym ośmiokąta foremnego. Leży on w odległości od każdego z wierzchołków. Oblicz pole ośmiokąta.
Każdy z boków trójkąta równobocznego podzielono na trzy równe części. Połączono punkty podziału i otrzymano sześciokąt foremny. Oblicz pole tego sześciokąta, jeżeli bok trójkąta ma długość .
Bok kwadratu ma długość . Każdy z boków tego kwadratu podzielono na trzy równe części. Połączono punkty podziału i otrzymano ośmiokąt. Oblicz pole tego ośmiokąta.