Prezentacja multimedialna
Polecenie 1
Zapoznaj się z prezentacją multimedialną przedstawiającą różne typy asymptot.
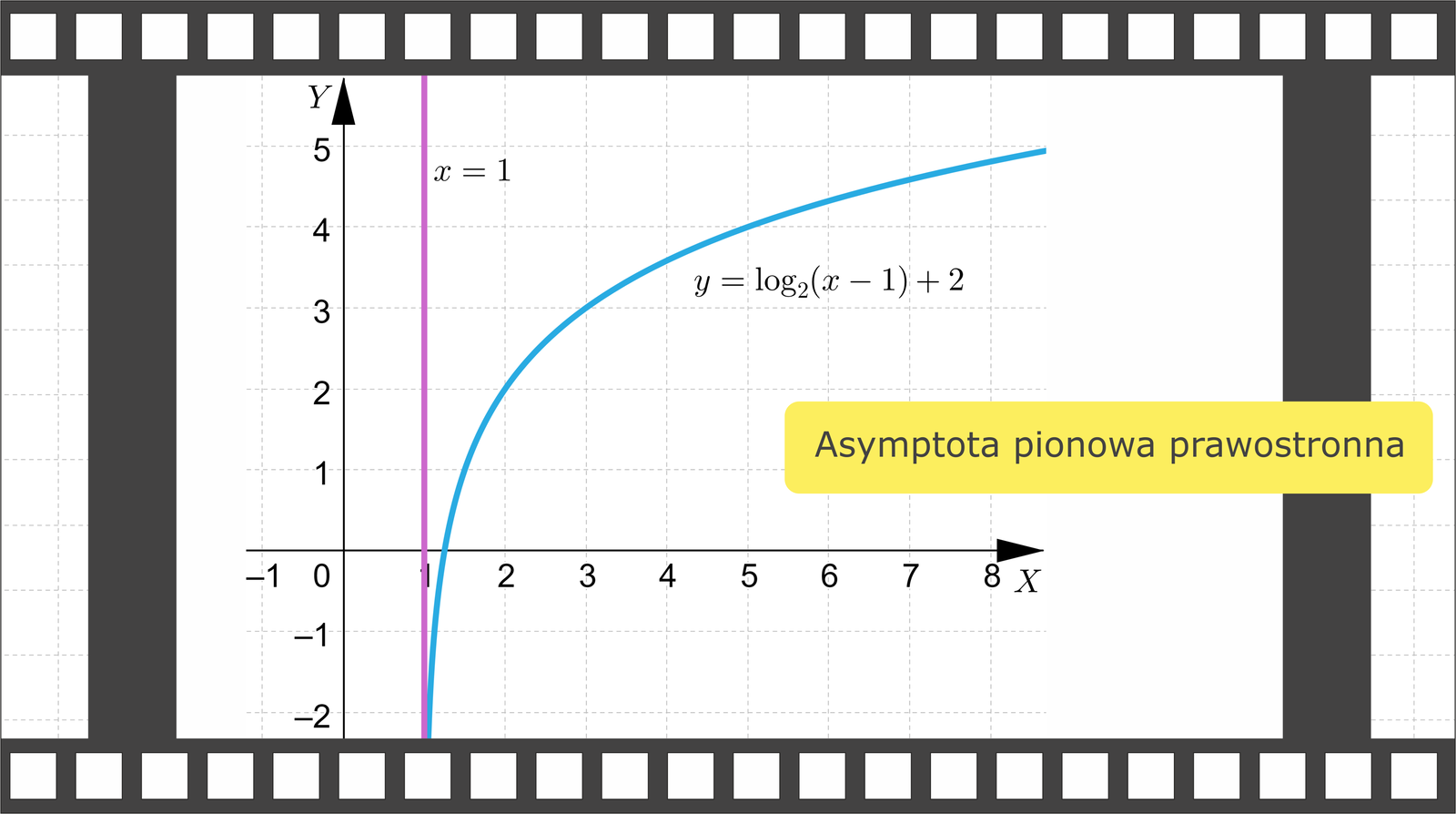
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DrZWeSNZg
Polecenie 2
Wykaż, że parabola o równaniu jest asymptotą wykresu funkcji .