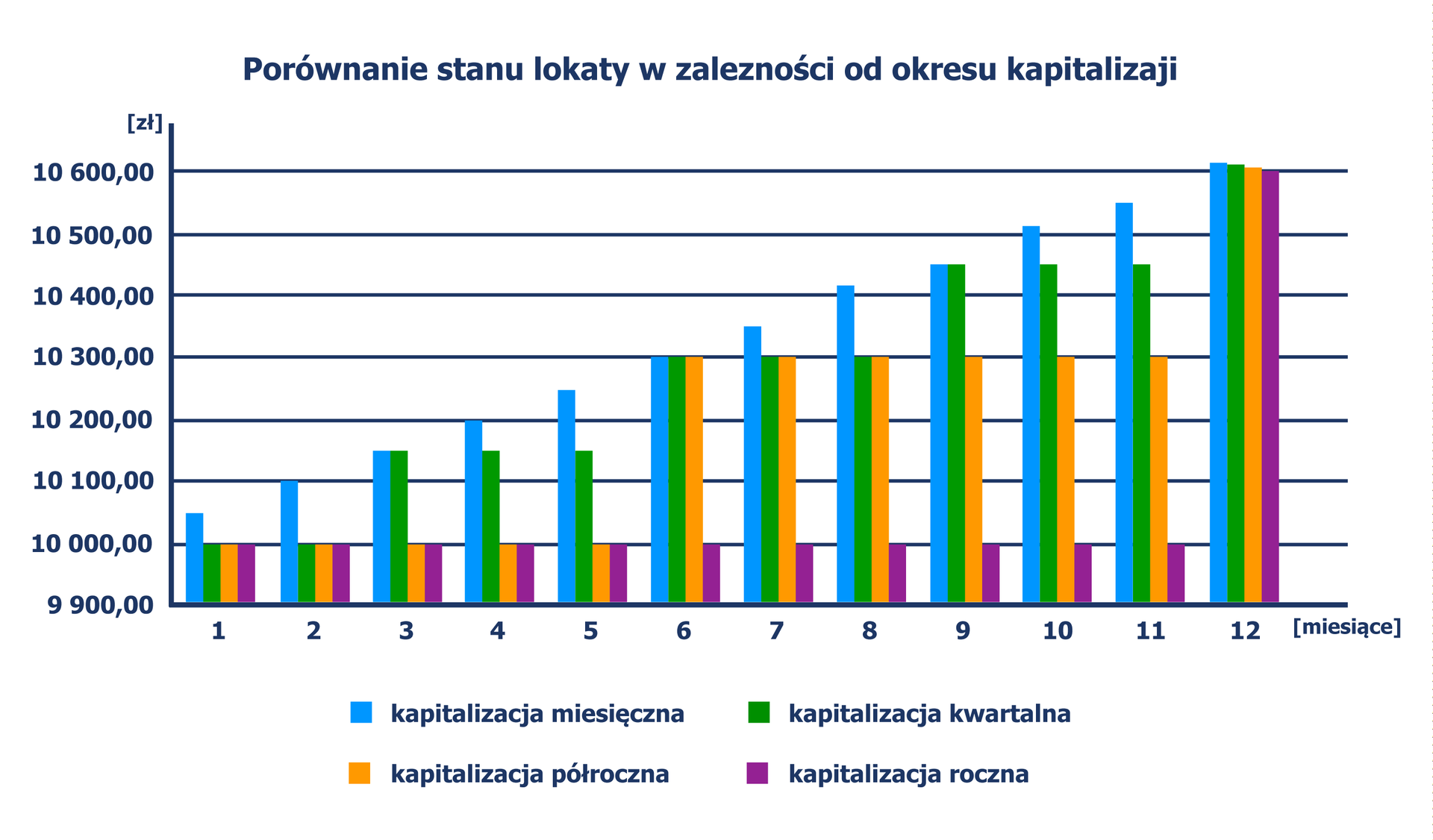
Procent składany
Lokatę bankową możemy traktować jako umowę zawartą między klientem a bankiem, na mocy której klient powierza bankowi określoną kwotę na ustalony termin. W zamian za to, po upływie tego terminu, bank wypłaca klientowi wpłaconą kwotę powiększoną o odsetki, które zostały naliczone zgodnie z warunkami zapisanymi w umowie. Istotny wpływ na wysokość ostatecznie wypłaconej kwoty ma, oczywiście, oprocentowanie lokaty, ale ważne jest również to, co dzieje się z naliczonymi po kapitalizacji odsetkami:
mogą one zostać przelane na inny rachunek tego samego klienta – wtedy kwota lokaty się nie zmienia i odsetki naliczone przy kolejnej kapitalizacji będą takie same - taki sposób obliczania odsetek nazywa się procentem prostym;
mogą zostać dopisane do lokaty – wtedy kwota lokaty zwiększa się o odsetki, które biorą udział w wypracowaniu zysku w kolejnym okresie – ten sposób nazywamy procentem składanym.
W zadaniach w tym rozdziale, mówiąc o lokacie bankowej, przyjmiemy, że każdorazowo po kapitalizacji odsetki dopisywane są do lokaty i lokata nie została zerwana przed upływem ustalonego terminu.
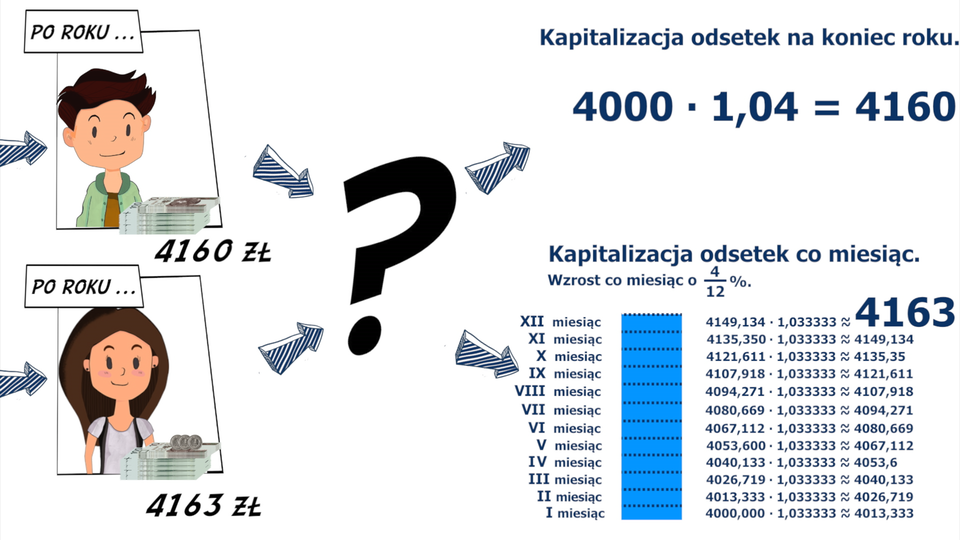
Film dostępny pod adresem /preview/resource/R1A7mvJpyrHW4
Animacja przedstawia dwóch chłopców, z których każdy wpłacił 4000 zł do banku na roczną lokatę. Jeden wpłacił do banku, gdzie lokata ma oprocentowanie 4% a drugi wybrał bank, gdzie oprocentowanie miesięczne jest 4%. Po roku pierwszy chłopiec otrzymuje 4160 zł a drugi 4163 złotych. Jak to się stało? Bank pierwszy - kapitalizuje odsetki na koniec lokaty, czyli mamy 4000 razy 1,04 =4160 zł. Bank drugi - kapitalizuje odsetki co miesiąc, czyli mamy: cztery dwunaste % , czyli co miesiąc 4000 x 1,00333333, potem 4013,33 x 1,0033333 itd. Zmiany będą jeszcze większe, gdy czas lokaty będzie dłuższy oraz kwota większa. Zatem wartość zarobionych pieniędzy zależy nie tylko od wysokości oprocentowania ale też od częstości kapitalizacji odsetek.
Pani Joanna wpłaciła do banku na pięcioletnią lokatę „Premium”. Warunki lokaty zakładają roczne oprocentowanie w wysokości i roczną kapitalizację odsetek. Jaki kapitał zostanie zgromadzony na lokacie po latach od jej założenia?
Prześledzimy krok po kroku zmiany tej lokaty.
Kapitał początkowy jest równy .
Lokata będzie utrzymywana przez lat i kapitalizacja będzie następowała co rok.
Mamy zatem okresów kapitalizacji ().
Oprocentowanie w okresie kapitalizacji jest równe .
Obliczmy kapitał zgromadzony po kolejnych latach
po pierwszym roku
Kwota lokaty zwiększyła się o z , czyli o .
po drugim roku
Podstawę do naliczenia odsetek stanowi teraz kwota , czyli otrzymamy
Kwota lokaty zwiększyła się o z , czyli o .
po trzecim roku
Podstawę do naliczenia odsetek stanowi teraz kwota powiększona o kolejne odsetki, czyli Po następnej kapitalizacji otrzymamy
Kwota lokaty zwiększyła się o z , czyli o .
Zauważmy, że w każdym roku doliczamy inną kwotę odsetek. Wynika to z tego, że za każdym razem inna jest podstawa ich naliczania.
Kwoty lokaty po kolejnych latach są kolejnymi wyrazami ciągu geometrycznego o ilorazie i wyrazach:
Wykorzystując wzór na -ty wyraz ciągu geometrycznego, otrzymujemy:
po czwartym roku
po piątym roku
Z tego wynika, że po latach pani Joanna powinna otrzymać .
W polskim systemie monetarnym najmniejszą jednostką jest , dlatego wszystkie kwoty zaokrąglamy z dokładnością do .
Od roku w Polsce obowiązuje podatek od dochodów kapitałowych. Oznacza to, że przy każdej kapitalizacji dopisywane odsetki zostaną pomniejszone o ich wartości.
W zadaniach w tym rozdziale kwotę podatku od dochodów kapitałowych będziemy pomijać.
Kwotę lokaty po okresach kapitalizacji można obliczyć, korzystając ze wzoru:
gdzie:
oznacza kapitał początkowy,
oznacza kapitał zgromadzony na lokacie po okresach kapitalizacji,
oznacza liczbę kapitalizacji,
oznacza oprocentowanie lokaty w okresie, po którym następuje kapitalizacja.
Pani Joanna wpłaciła na lokatę z rocznym oprocentowaniem w wysokości oraz z miesięczną kapitalizacją odsetek. Jaką kwotę zgromadzi ona na tej lokacie po roku od jej założenia?
W tym przykładzie mamy
Lokata będzie utrzymywana przez rok, natomiast odsetki będą dopisywane co miesiąc. Mamy zatem okresów kapitalizacji ().
Oprocentowanie roczne jest równe , zatem w pojedynczym okresie kapitalizacji wyniesie
Obliczmy kapitał zgromadzony po miesiącach
Przedstawiony powyżej sposób obliczania kapitału końcowego zakłada, że obliczamy od razu wartość końcową po okresach kapitalizacji. Pomijamy tym samym wszystkie kwoty pośrednie – po pierwszym, drugim i kolejnych kapitalizacjach.
W rzeczywistości jest inaczej – każdorazowo kwota po dopisaniu odsetek jest zaokrąglana do i otrzymane przybliżenie jest podstawą do obliczenia odsetek w następnym okresie. Przy wielokrotnej kapitalizacji ostateczne kwoty kapitału końcowego mogą się nieznacznie różnić.
Musimy zatem pamiętać, że wzór na procent składany jest tylko matematycznym przybliżeniem rzeczywistości bankowej.

Film dostępny pod adresem /preview/resource/RMj5lEjHuvSZq
W animacji przedstawiono rozwiązanie zadania. Dane: kapitał początkowy wynosi 1000 złotych, czas trwania lokaty wynosi 1 rok, kapitalizacja odsetek jest co miesiąc, liczba kapitalizacji w roku wynosi 12, oprocentowanie roczne wynosi 6 procent, a oprocentowanie w okresie kapitalizacji wynosi 6 procent podzielić na 12 równa się pół procent. Prześledzimy jak zmienia się wartość tej lokaty w pierwszych miesiącach. Rozwiązanie. Po pierwszym miesiącu mamy: , stąd , zatem ostatecznie mamy: . Czyli po pierwszym miesiącu kwota na lokacie zwiększyła się o 5 złotych. Po drugim miesiącu mamy: , stąd , zatem ostatecznie mamy: . Zatem kwota lokaty zwiększyła się o pół procent z tysiąca pięciu złotych, czyli po drugim miesiącu kwota na lokacie zwiększyła się o 5 złotych i trzy grosze. Po trzecim miesiącu mamy: , stąd , zatem ostatecznie mamy: . Zatem kwota lokaty zwiększyła się o pół procent z tysiąca dziesięciu złotych i trzech groszy, czyli po drugim miesiącu kwota na lokacie zwiększyła się o 5 złotych i pięć groszy. Zauważmy, że w każdym miesiącu doliczamy inną kwotę odsetek. Wynika to z tego, że za każdym razem inna jest podstawa ich naliczania. Mamy więc , , , . Otrzymane kwoty są kolejnymi wyrazami ciągu geometrycznego o ilorazie q równym 1,0005. Wykorzystując wzór na dowolny wyraz ciągu geometrycznego, otrzymujemy: stan konta po czwartym miesiącu wyniesie: , po piątym miesiącu wyniesie: , analogicznie po roku, czyli po dwunastu okresach kapitalizacji wyniesie po piątym miesiącu wyniesie: . Z tego wynika, że po roku pani Joanna powinna wypłacić 1068 złotych i 68 groszy. Uwaga. Niestety w rzeczywistości pani Joanna wypłaci mniejszą kwotę. Od 2002. roku w Polsce obowiązuje podatek od dochodów kapitałowych. Oznacza to, że przy każdej kapitalizacji dopisywane odsetki zostaną pomniejszone o 19 procent ich wartości. Kwotę lokaty po n okresach kapitalizacji można obliczyć, korzystając ze wzoru , gdzie K p to kapitał początkowy, K n to kapitał zgromadzony na lokacie po n okresach kapitalizacji, n to liczba kapitalizacji, a p jest oprocentowaniem lokaty w okresie, po którym następuje kapitalizacja.
Na realizację marzeń o wycieczce do Afryki Justyna potrzebuje co najmniej . Postanowiła systematycznie, co miesiąc, odkładać . Bank zaproponował lokatę z możliwością dopłacania pieniędzy, oprocentowaną rocznie z miesięczną kapitalizacją odsetek. Czy po miesiącach oszczędzania Justyna zgromadzi odpowiednią kwotę?
Przeanalizujmy krok po kroku zmiany na tej lokacie.
Oprocentowanie w okresie kapitalizacji
Stan lokaty po pierwszym miesiącu
Stan lokaty po drugim miesiącu
Stan lokaty po trzecim miesiącu
Stan lokaty po czwartym miesiącu
Zauważmy, że ulokowane w pierwszym miesiącu procentuje najdłużej, kolejne – miesiąc krócej i tak dalej, aż do ostatniej wpłaconej kwoty, która procentuje tylko miesiąc.
Stan lokaty po miesiącach oszczędzania możemy zapisać
Jest to suma osiemnastu kolejnych wyrazów ciągu geometrycznego, w którym , .
Wartość lokaty po miesiącach będzie sumą osiemnastu wyrazów ciągu geometrycznego
.
Zatem Justyna jest bliska zgromadzenia potrzebnej kwoty , ale brakuje jej jeszcze około .
Musimy pamiętać, że przedstawiane zadania i przykłady zastosowania procentu składanego nie zawsze są wiernym odwzorowaniem rzeczywistości bankowej. Oferta lokat bankowych jest bardzo bogata i zróżnicowana. Systemy obliczeniowe stosowane w bankach pozwalają na zmianę oprocentowania w różnych okresach trwania lokaty, częstą kapitalizację lub nawet możliwość wypłaty części środków z lokaty przed upływem zadeklarowanego okresu. Ponadto od roku obowiązuje, wspomniany wcześniej, podatek od dochodów kapitałowych, który każdorazowo zmniejsza kwotę należnych odsetek o ich wartości.
Bank proponuje trzy rodzaje lokat:
lokata - miesięczna, z rocznym oprocentowaniem wynoszącym . Minimalna kwota jaką można wpłacić na tą lokatę to . Po zakończeniu trwania lokaty, odsetki zostają dopisane do lokaty. Lokata może być odnawiana na kolejne okresy.
lokata - miesięczna, z rocznym oprocentowaniem wynoszącym . Minimalna kwota jaką można wpłacić na tą lokatę to . Po zakończeniu trwania lokaty, odsetki zostają dopisane do lokaty. Lokata może być odnawiana na kolejne okresy.
lokata - miesięczna, z rocznym oprocentowaniem wynoszącym . Minimalna kwota jaką można wpłacić na tą lokatę to . Po zakończeniu trwania lokaty, odsetki zostają dopisane do lokaty. Lokata może być odnawiana na kolejne okresy.
Która z nich jest najbardziej korzystna, jeśli chcemy ulokować na okres lat?