Przeczytaj
Najprostszym i najczęściej wykorzystywanym narzędziem w arkuszu kalkulacyjnym służącym do prognozowania danych jest Arkusz prognozy. Dzięki zastosowaniu tego narzędzia możemy na podstawie danych historycznych w szybki i czytelny sposób wyznaczyć m.in. przyszły poziom sprzedaży, wymagany poziom zapasów, różnego rodzaju wskaźniki (demograficzne, makroekonomiczne, pogodowe) czy też trendy konsumpcyjne.
Pobierz przykładowe dane:
Arkusz prognozy
Prześledźmy działanie tego narzędzia na podstawie firmy, której wyniki sprzedażowe za pierwsze półrocze 2020 roku wyglądają następująco.
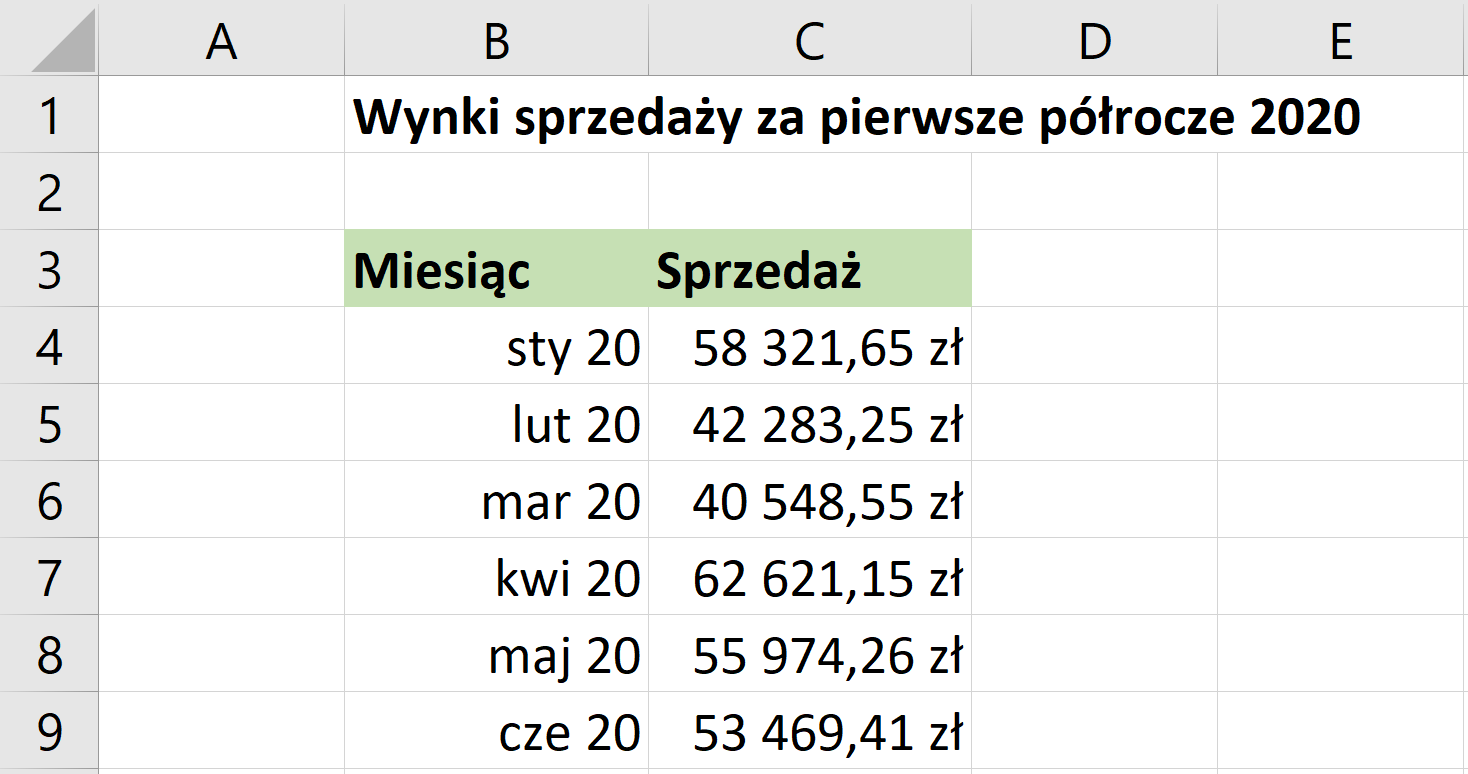
Na podstawie wyników osiągniętych w pierwszych sześciu miesiącach, przy założeniu, że firma działa w branży, która nie charakteryzuje się zbyt dużą sezonowością, a więc popyt na sprzedawane towary/usługi utrzymuje się na tym samym poziomie przez cały rok, możemy za pomocą narzędzia Arkusz prognozy przeprowadzić symulację spodziewanych przychodów w drugim półroczu. Ważne jest jednak, aby prawidłowo zdefiniować oś czasu. Prognozowanie zadziała tylko wówczas, gdy oś czasu będzie zawierała spójne interwały czasowe, np. dni, miesiące, kwartały, lata.
Po zaznaczeniu obszaru danych wykorzystywanych do prognozy, tj. zakres B3:C9, ze wstążki wybieramy zakładkę Dane, a z obszaru Prognoza wybieramy Arkusz prognozy.
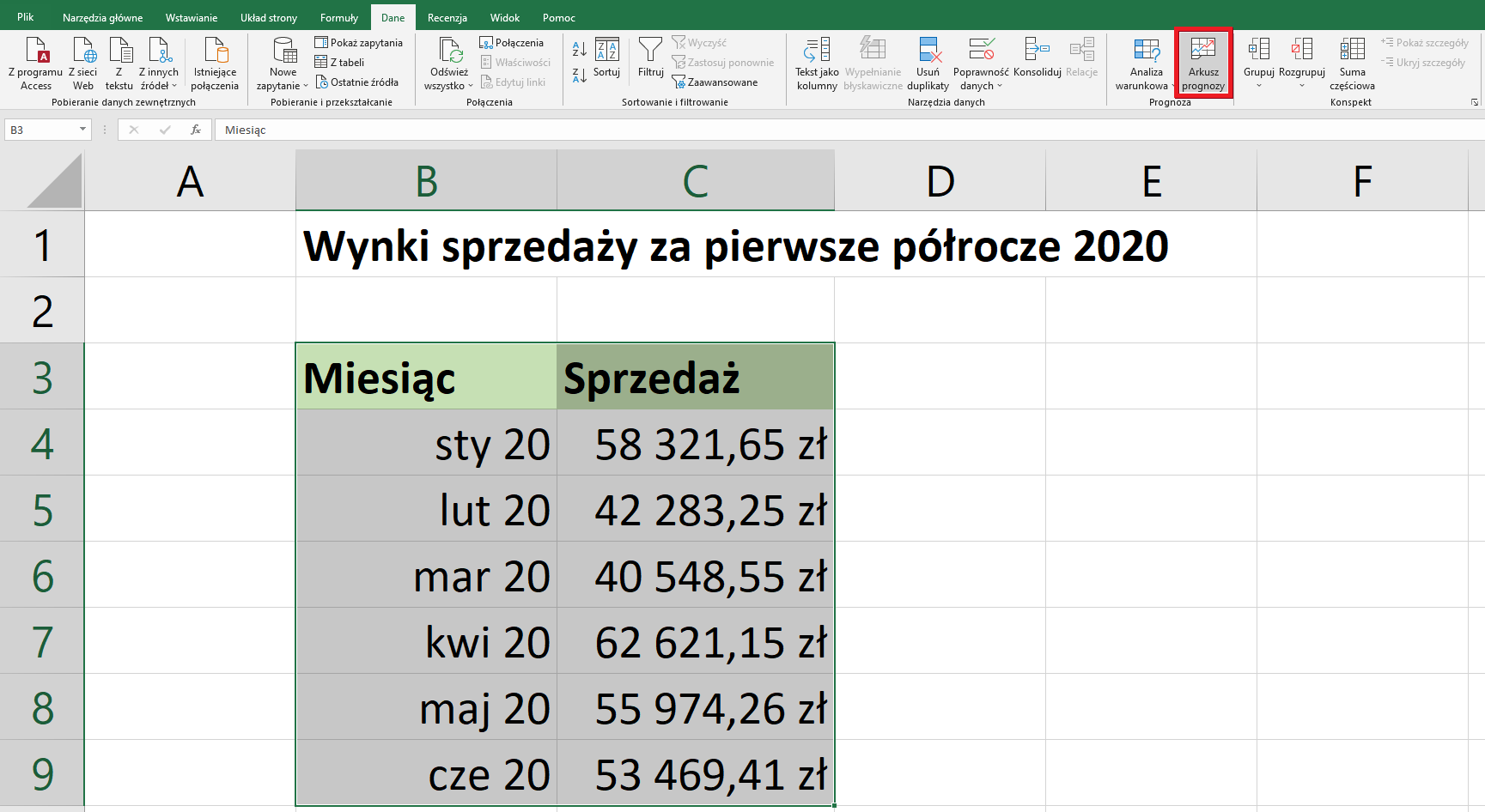
Pojawia się okno Tworzenie arkusza prognozy, dzięki któremu możemy ustalić parametry prognozy i dostosować ją do naszych potrzeb.
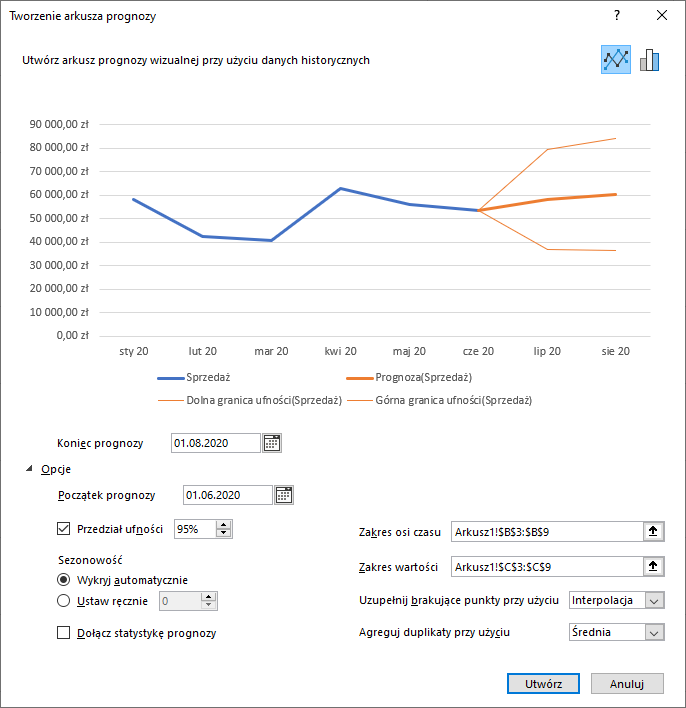
Na tym etapie możemy wybrać sposób graficznego przedstawienia prognozy (w prawym górnym rogu mamy możliwość wybrania wykresu liniowego lub kolumnowego), a także określić końcową datę prognozy. Dodatkowo po rozwinięciu zakładki Opcje możemy m.in. zmienić początkową datę prognozy, ustalić poziom przedziału ufności czy też sposób wykrywania przez narzędzie występowania sezonowości. Z reguły do wykonania prognozy wystarczy skorzystać z domyślnych ustawień. Jeśli chcemy zmienić poszczególne ustawienia, to warto pamiętać, co one oznaczają. I tak:
określa poziom prawdopodobieństwa, z jakim prognozowany parametr uzyska w rzeczywistości daną wartość (domyślny poziom w wys. 95% wskazuje na bardzo duże prawdopodobieństwo, że prognozowane dane rzeczywiście będą się w przyszłości kształtowały na takim poziomie)
opcja Wykryj automatycznie pozwala na automatyczne odnalezienie w badanym okresie regularnie występujących różnic pomiędzy analizowanymi wartościami; dla pewnego przedziału czasu, mniejszego od roku, np. tygodnia, miesiąca, kwartału;
ta opcja jest wykorzystywana w sytuacji, gdy w analizowanym zestawieniu brakuje jakiejś wartości, np. w zestawieniu rocznym brakuje danych za jeden miesiąc. W takiej sytuacji arkusz kalkulacyjny zastosuje interpolację, czyli jako wartość brakującej pozycji przyjmie średnią ważoną sąsiednich pozycji (waga średniej ważonej jest automatycznie określana przez arkusz kalkulacyjny i sami nie możemy jej określić)
w sytuacji, gdy w analizowanym zestawieniu zostaną zdublowane pozycje, np. przez pomyłkę w zestawieniu znajdą się dwie wartości dla jednego miesiąca, wówczas arkusz kalkulacyjny przyjmie dla tej pozycji wartość uśrednioną
W analizowanym przypadku interesuje nas prognoza na drugie półrocze, tak więc ustalamy koniec prognozy na dzień 1.12.2020 (mimo że wskazana jest data na pierwszy dzień miesiąca, to w domyśle prognoza dotyczyć będzie wyników za cały miesiąc grudzień), a w przypadku pozostałych parametrów korzystamy z domyślnych ustawień. Całość zatwierdzamy przyciskiem Utwórz.
W rezultacie arkusz kalkulacyjny tworzy nowy arkusz, w którym przedstawione są prognozowane za dany okres wyniki w ujęciu tabelarycznym oraz graficznym.
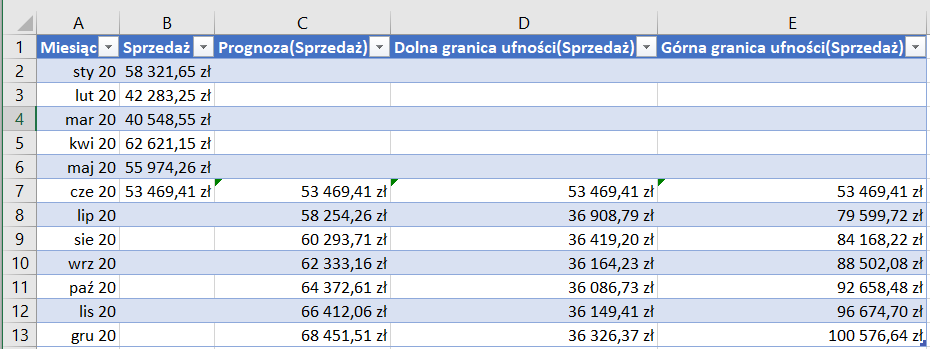
W komórce C8 została zastosowana formuła =REGLINX.ETS(A8;$B$2:$B$7;$A$2:$A$7;1;1). Omówmy ją, aby dobrze zrozumieć jej działanie.
Funkcja REGLINX.ETS przy pomocy algorytmu wygładzania wykładniczego (ETS) oblicza wartości prognozowane na podstawie istniejących wartości. Składnia tej funkcji wygląda następująco:
REGLINX.ETS(data_docelowa;wartości;oś_czasu;[sezonowość];[kompletność_danych];[agregacja])data_docelowa– punkt, na podstawie i dla którego zostanie obliczona prognoza. Może to być data, godzina lub wartość liczbowa. Jest to argument wymagany.wartości– wartości historyczne, na podstawie których obliczone zostaną prognozowane wartości. Jest to argument wymagany.oś_czasu– tablica lub zakres danych z okresami dla których wartości są znane. Wartości te muszą mieć spójną relację między kolejnymi okresami oraz nie mogą być zerowe. Jest to argument wymagany.[sezonowość]– argument opcjonalny, który na podstawie podanej wartości liczbowej przyjmuje sposób obliczania sezonowości. Domyślnie argument ustawiony jest na 1 i sprawi, że arkusz automatycznie wykrywa sezonowość prognozy i używa dodatnich liczb całkowitych dla długości wzorca sezonowości. 0 wskazuje brak sezonowości, co oznacza, że prognoza będzie liniowa. Dodatnia liczba całkowita wskazuje, że algorytm ma używać wzorców tej długości jako sezonowości. Podanie każdej innej liczby sprawi, że funkcja zwróci błąd.[kompletność_danych]– argument opcjonalny, który przyjmuje wartość 0 lub 1. Domyślna wartość 1 sprawi, że brakujące punkty będą uwzględnione, a zostaną one uzupełnione jako średnie wartości sąsiadujących punktów. Wartość 0 sprawi, że brakujące punkty będą traktowane jak zera. Nie może brakować więcej niż 30% wartości historycznych.[agragacja]– argument opcjonalny, który jest wartością liczbową wskazującą, która metoda zostanie użyta do agregowania kilku wartości z jednakową sygnaturą czasową.
Agregacja | Funkcja |
|---|---|
1 (wartość domyślna) |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
W komórce D8 została zastosowana formuła
=C8-REGLINX.ETS.CONFINT(A8;$B$2:$B$7;$A$2:$A$7;0,95;1;1)a w komórce E8 niemalże identyczna formuła jednak został zmieniony znak z minus na plus. Omówmy działanie funkcji REGLINX.ETS.CONFINT.
Funkcja ta zwraca najmniejszą wartość, kóra może wystąpić dla podanego punktu z uwzględnieniem przedziału ufności. Składnia tej funkcji wygląda następująco:
REGLINX.ETS.CONFINT(data_docelowa;wartości;oś_czasu;[poziom_ufności];[sezonowość];[kompletność_danych];[agregacja])Argumenty działają dokładnie tak samo jak dla omawianej wyżej funkcji REGLINX.ETS. Dodatkowy opcjonalny argument [poziom_ufności] jest wartością liczbową z przedziału (0, 1) i wskazuje poziom ufności. Wartość domyślna to 0,95, a więc 95%.
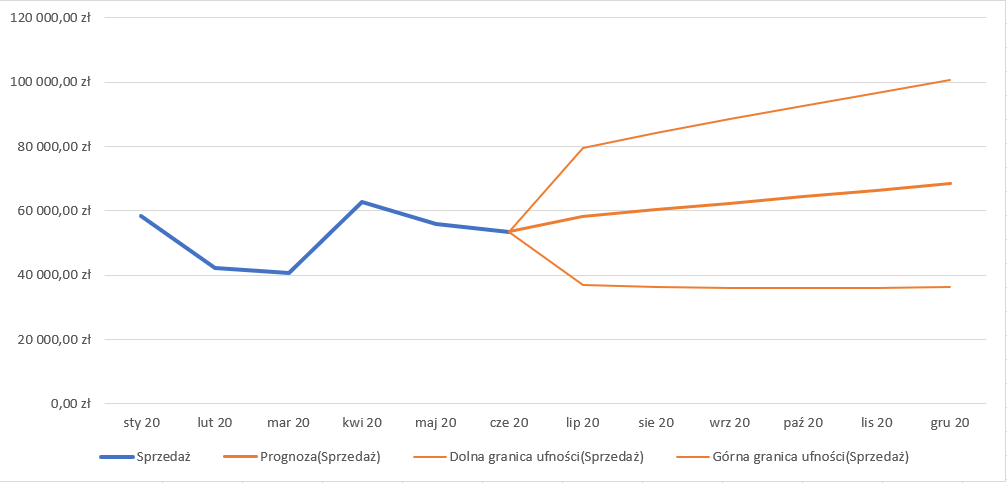
Na wykresie prognoza zaznaczona jest pogrubioną linią w kolorze innym niż dotychczasowe wyniki (w omawianym przypadku jest to kolor pomarańczowy). Oprócz linii głównej zauważyć też można dwie cienkie linie oznaczające przedział ufności, a więc zakres, w jakim powinno mieścić się 95% prognozowanych wartości dla każdego miesiąca.
Sezonowość
Ważnym aspektem podczas prognozowanie jest także uwzględnienie sezonowości. W niektórych branżach sezonowość odgrywa dużą rolę, więc prognozując przyszłe wyniki, warto jest wziąć również ten czynnik pod uwagę. Sezonowość zwykle jest uzależniona od pogody, pory roku, okresu wakacji lub świąt, czy też innych sytuacji powtarzających się w tym samym czasie.
Analogicznie do poprzedniego przykładu wykonajmy prognozę sprzedaży dla firmy zajmującej się sprzedażą i wynajmem sprzętu narciarskiego. W pliku załącznika znajdują się wyniki sprzedażowe firmy za lata 2020, 2021 oraz pierwsze półrocze 2022 roku. Aby prognoza uwzględniała sezonowość sprzedaży przeprowadźmy symulację sprzedaży w kolejnych 12 miesiącach. W tym celu ponownie zaznaczamy obszar danych, na podstawie których ma być przeprowadzona analiza i ze wstążki wybieramy zakładkę Dane, a z obszaru Prognoza wybieramy Arkusz prognozy. Otrzymujemy w ten sposób następujący wynik.
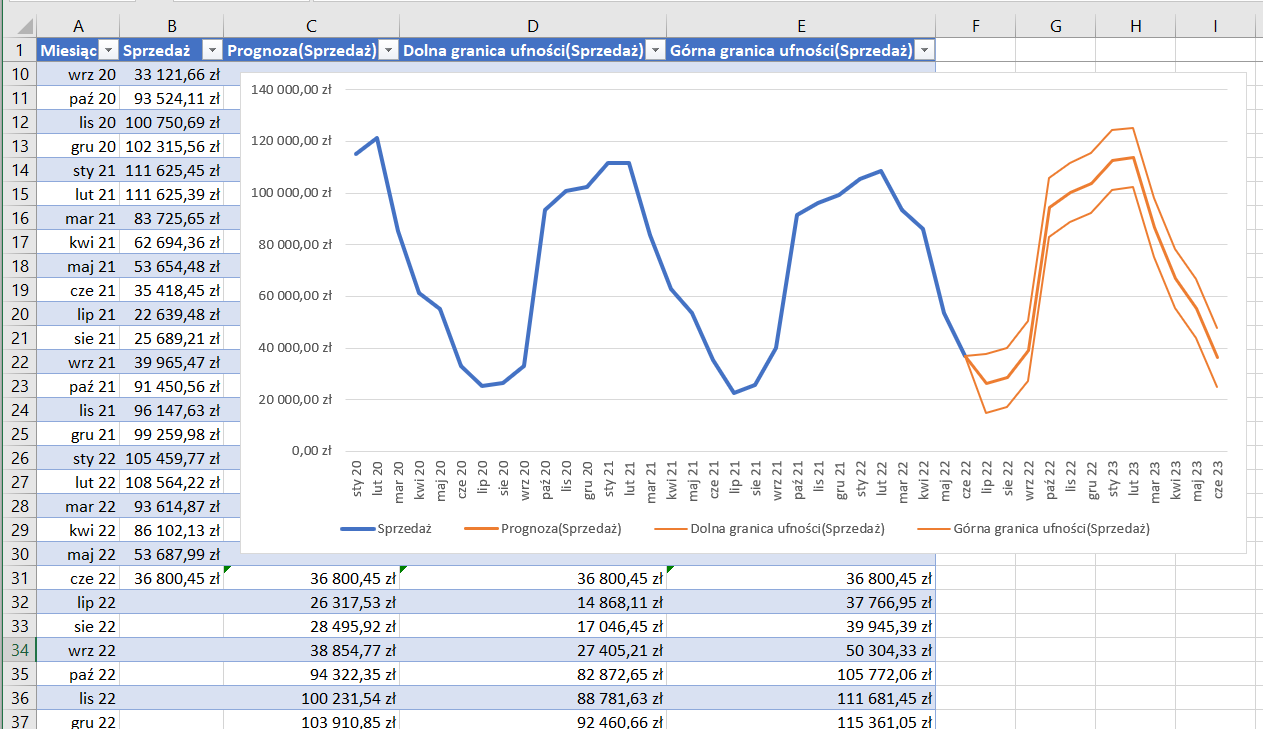
Jak widać, dotychczasowe wyniki firmy były mocno uzależnione od pory roku. W miesiącach zimowych, tj. od października do lutego, można zaobserwować wyraźny wzrost sprzedaży i wynajmu sprzętu narciarskiego. W pozostałym okresie sprzedaż jest zdecydowanie niższa. Taki trend ma również odzwierciedlenie w prognozie, która na podstawie historycznych danych pokazuje, że w kolejnych dwunastu miesiącach istnieje bardzo duże prawdopodobieństwo, że ten trend zostanie utrzymany, a więc firma może spodziewać się w tych miesiącach większego popytu na swoje towary i usługi. Wykonana w ten sposób prognoza pozwala zarządzającym firmą nie tylko oszacować przyszłe zyski, lecz również pokazuje, na jakie stany magazynowe należy się przygotować w kolejnych miesiącach.
Program LibreOffice Calc nie posiada funkcjonalności Arkusz prognozy. W programie LibreOffice Calc mamy możliwość prognozowania danych na dwa sposoby, jednak żaden z nich nie działa w ten sam sposób, co Arkusz prognozy.
Krzywa regresji
Prześledźmy działanie tego narzędzia na podstawie firmy, której wyniki sprzedażowe za pierwsze półrocze 2020 roku wyglądają następująco.
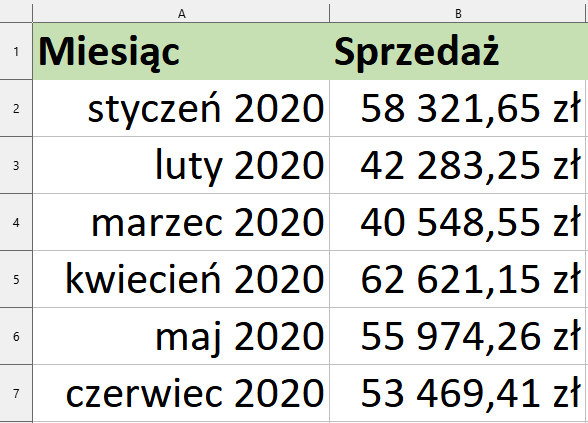
Do kolejnych komórek w kolumnie A dodajmy okresy, dla których chcemy stworzyć prognozę danych. W ramach przykładu dodajmy okresy do grudnia.
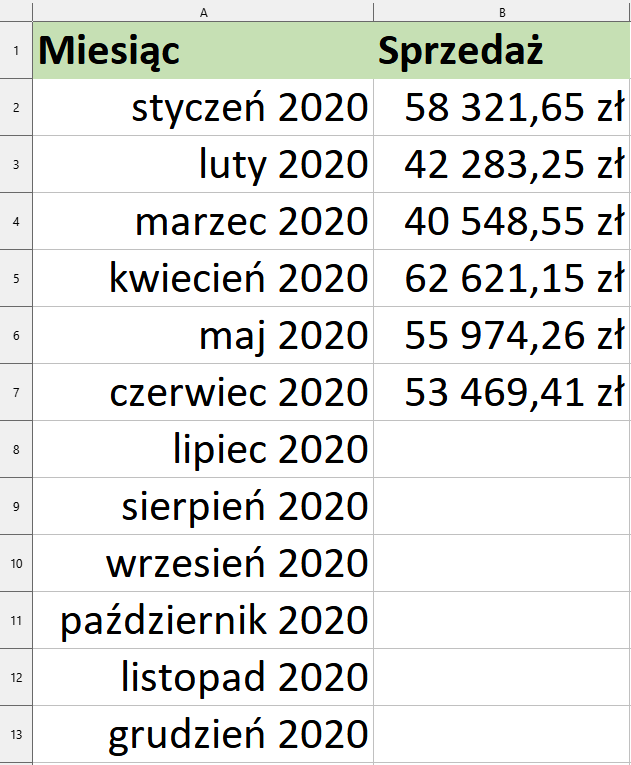
Dane przedstawimy na wykresie. Na nim będziemy mogli nanieść krzywą regresji, która w naszym przykładzie będzie prognozować dane. Zaznaczmy więc komórki z zakresu A1:B13. Z menu głównego wybieramy Wstaw, a następnie wybieramy opcję Wykres...
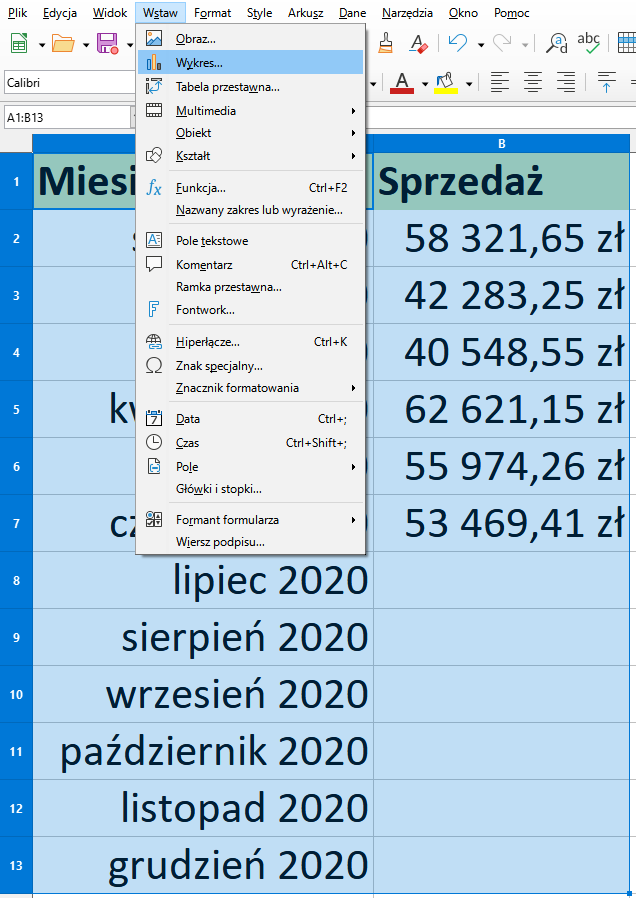
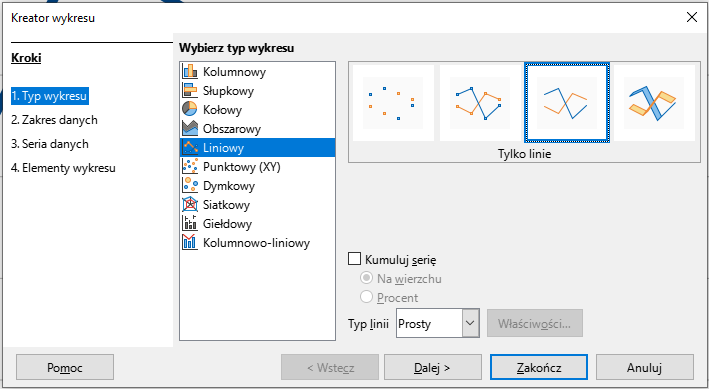
W oknie kreatora wykresu wybieramy liniowy typ wykresu – Tylko linie. Następnie potwierdzamy tworzenie wykresu przyciskiem Zakończ.
Na tym etapie tak prezentuje się wykres:
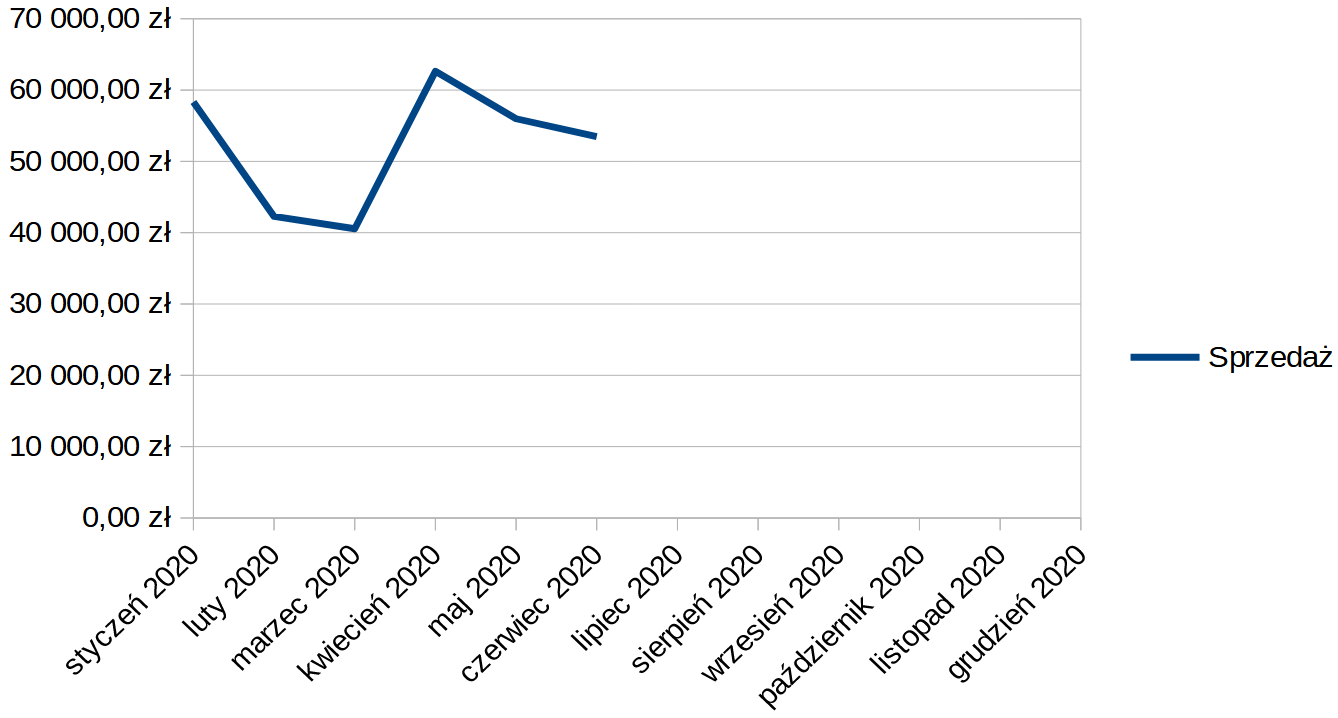
Jak widzimy, możemy odczytać z niego tylko dane rzeczywiste. Czas nanieść na wykres krzywą, która wskazywać będzie prognozowane wartości sprzedaży. Zaznaczmy obszar wykresu, następnie najeżdżamy kursorem na linię oznaczającą serię danych „Sprzedaż” i klikamy na nią prawym przyciskiem myszy. Z menu podręcznego wybieramy opcję Wstaw krzywą regresji...
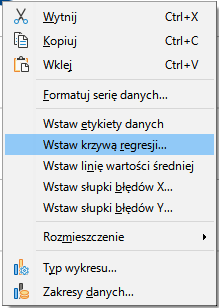
W wyświetlonym oknie tworzenia krzywej regresji kliknijmy przycisk OK, aby nanieść krzywą na wykres.
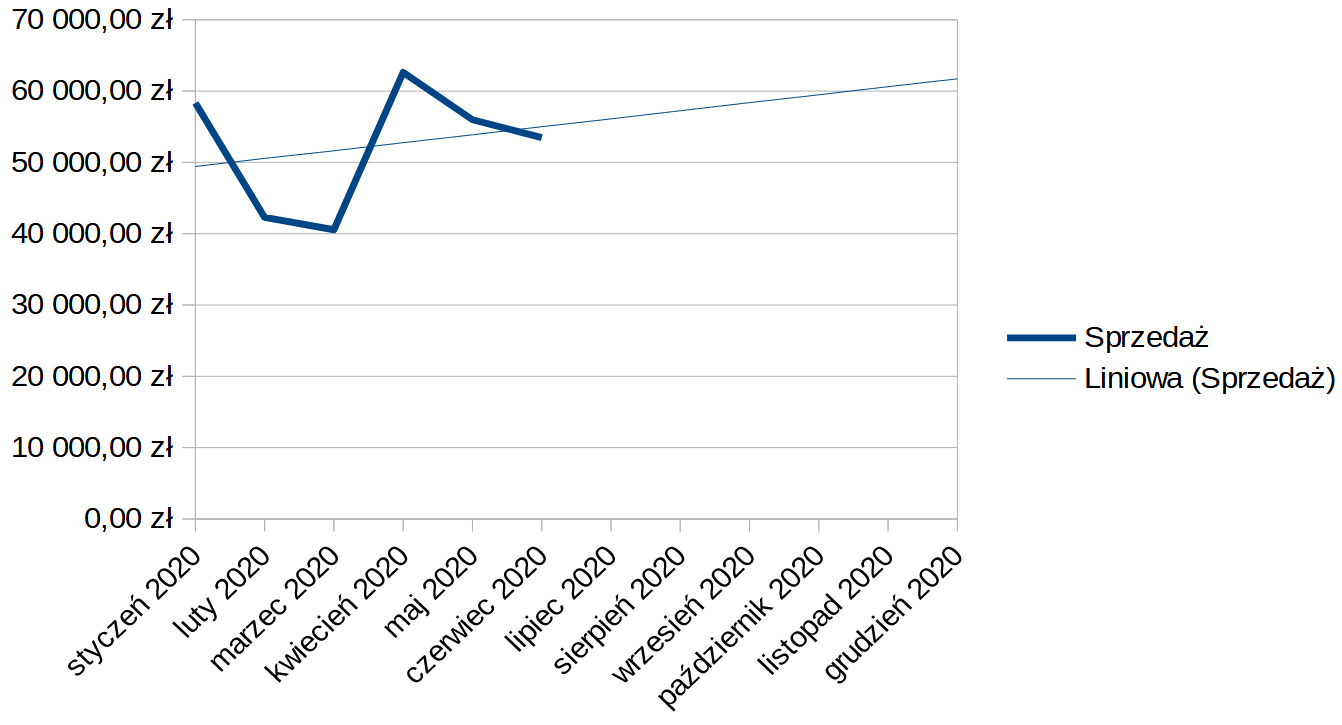
Dzięki automatycznie naniesionej na wykres krzywej regresji, możemy odczytać, że wartość sprzedaży w kolejnych miesiącach 2020 roku będzie rosła.
Więcej o tworzeniu krzywej regresji możesz przeczytać w e‑materiale Linie trendu w arkuszu kalkulacyjnymPqSzqtLSALinie trendu w arkuszu kalkulacyjnym
Funkcja REGLINX.ETS.ADD
W przypadku większej ilości danych, a zwłaszcza, gdy występują powtarzające się okresy, możemy skorzystać z funkcji REGLINX.ETS.ADD.
Funkcja ta za pomocą Podwójnego (EDS) lub Potrójnego (ETS) Wygładzania Wykładniczego oraz bazując na danych historycznych oblicza addytywnąaddytywnyaddytywną prognozę wartości. Oto składnia funkcji:
REGLINX.ETS.ADD(cele, wartości, oś czasu, [długość_okresu], [zakończenie_danych], [agregacja])cele – okres lub punkt, dla którego obliczamy prognozę.
wartości – zakres lub macierz, na podstawie których obliczone zostaną prognozowane wartości.
oś czasu – macierz lub zakres z datami, dla których znane są wartości.
[długość_okresu] – argument opcjonalny, oznacza metodę, za pomocą której obliczona zostanie prognoza. Wartość argumentu równa 1 (domyślna) lub dowolna liczba naturalna oznacza metodę ETS, a wartość 0 oznacza metodę EDS.
[zakończenie_danych] – argument opcjonalny, wartość logiczna – domyślnie 1 (PRAWDA) lub 0 (FAŁSZ). Wartość 0 (FAŁSZ) doda brakujące punkty danych wraz z zerem jako wartością historyczną. Wartość 1 (PRAWDA) doda brakujące punkty danych poprzez interpolację między sąsiednimi punktami danych.
[agregacja] – argument opcjonalny, liczba całkowita z przedziału <1, 7>, która oznacza metodę, za pomocą której elementy zostaną złączone w całość.
Agregacja | Funkcja |
|---|---|
1 (wartość domyślna) |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
Przejdźmy do zakładki Arkusz2 i sprawdźmy działanie tej funkcji na przykładzie.
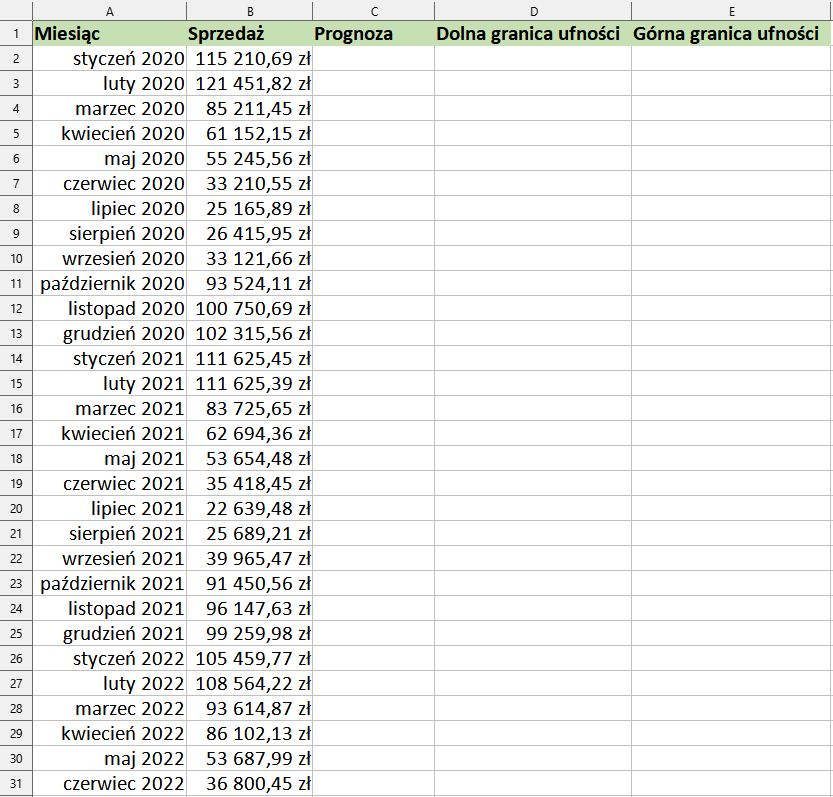
Wykonajmy prognozę sprzedaży dla firmy zajmującej się sprzedażą i wynajmem sprzętu narciarskiego. W arkuszu znajdują się wyniki sprzedażowe firmy za lata 2020, 2021 oraz pierwsze półrocze 2022 roku. Przeprowadźmy symulację sprzedaży w kolejnych 12 miesiącach.
W pierwszej kolejności do kolumny A musimy dodać daty, dla których chcemy obliczyć prognozę. Będą to kolejne miesiące od lipca 2022 do czerwca 2023, a do komórek C31:E31 skopiujemy wartość sprzedaży z komórki B31.
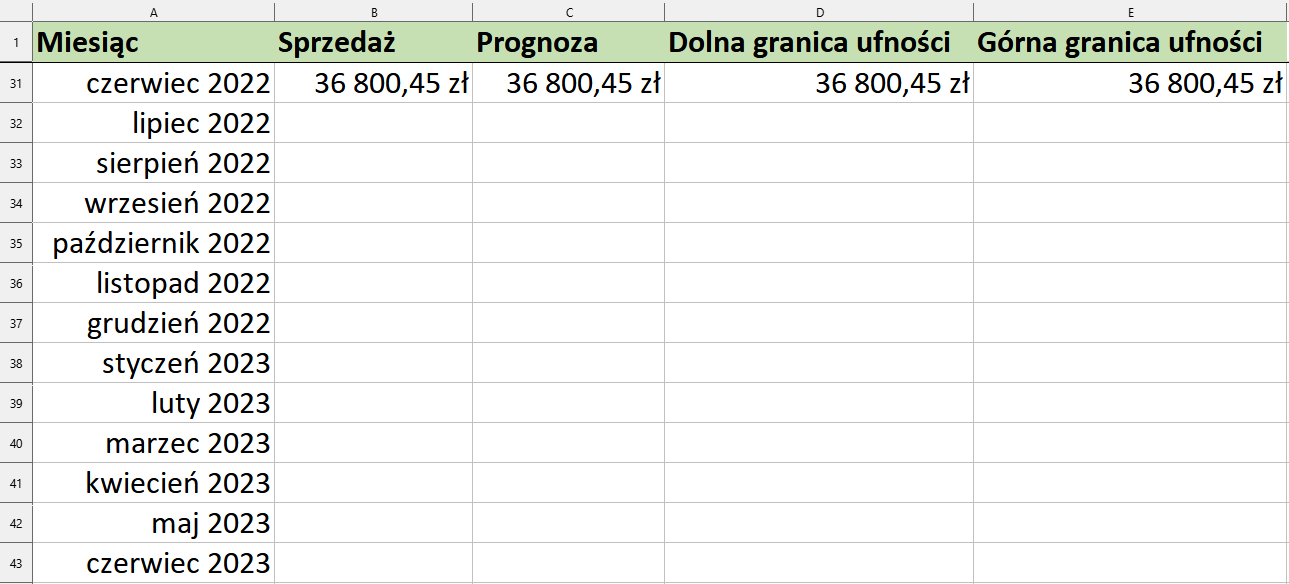
Przy tak przygotowanym arkuszu możemy rozpocząć prognozowanie wartości. Do komórki C32 wpiszemy formułę:
=REGLINX.ETS.ADD(A32;$B$2:$B$31;$A$2:$A$31)A następnie skopiujemy ją w dół aż do komórki C43.
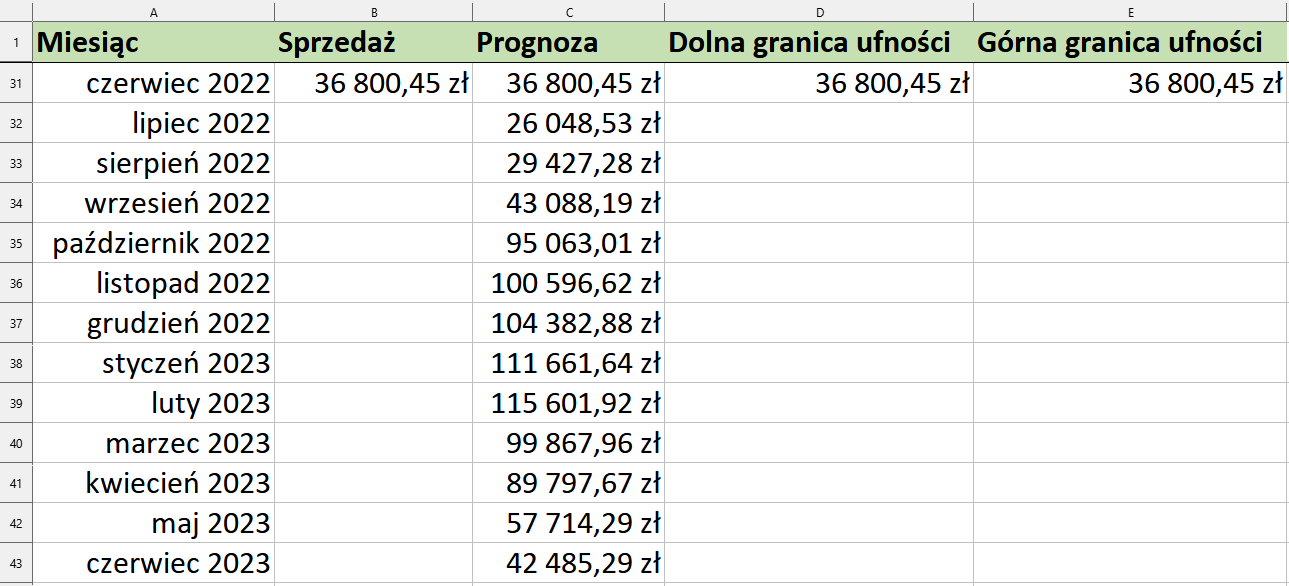
Teraz wyznaczymy dolną oraz górną granicę ufności. Zakładamy, że prognozowane wartości sprzedaży mogą wahać się o 5% zarówno w górę jak i w dół. Do komórki D32 wpiszemy więc formułę
=C32*0,95
A do komórki E32 wpiszemy formułę:
=C32*1,05
Obie formuły skopiujmy w dół, aż do wiersza o numerze 43.
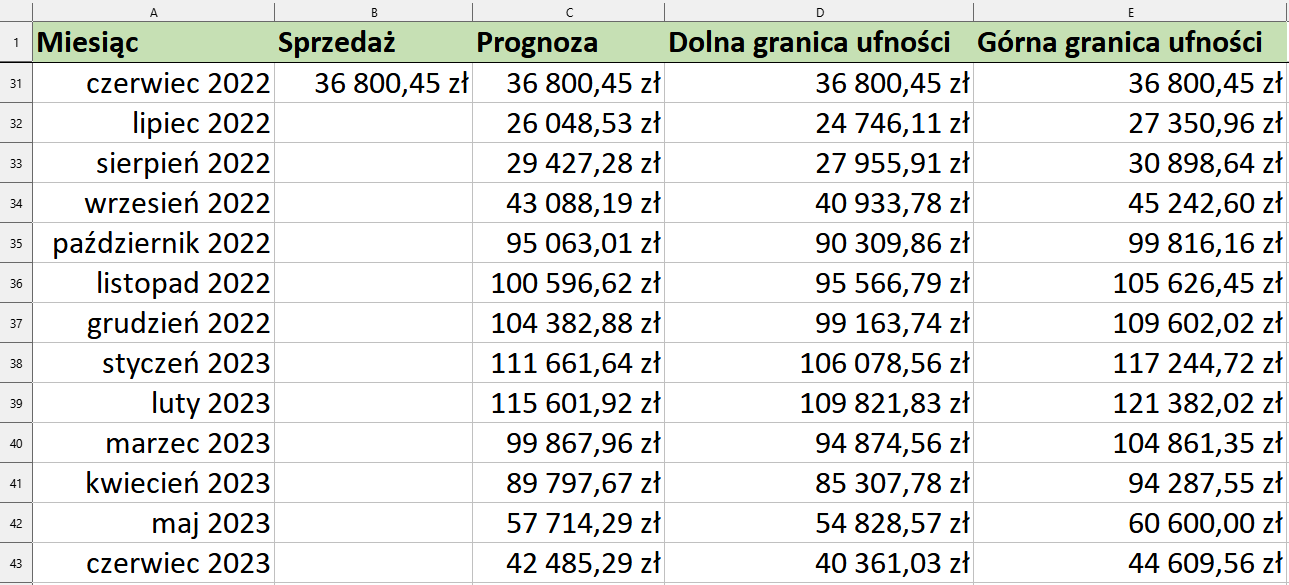
W ten sposób obliczyliśmy prognozowane wartości dla następnego roku wraz z granicami ufności. Pozostało nam przedstawić te wartości na wykresie. Zaznaczmy więc komórki z zakresu A1:E43, a następnie tworzymy wykres w ten sam sposób jak zostało to pokazane na poprzednim przykładzie.
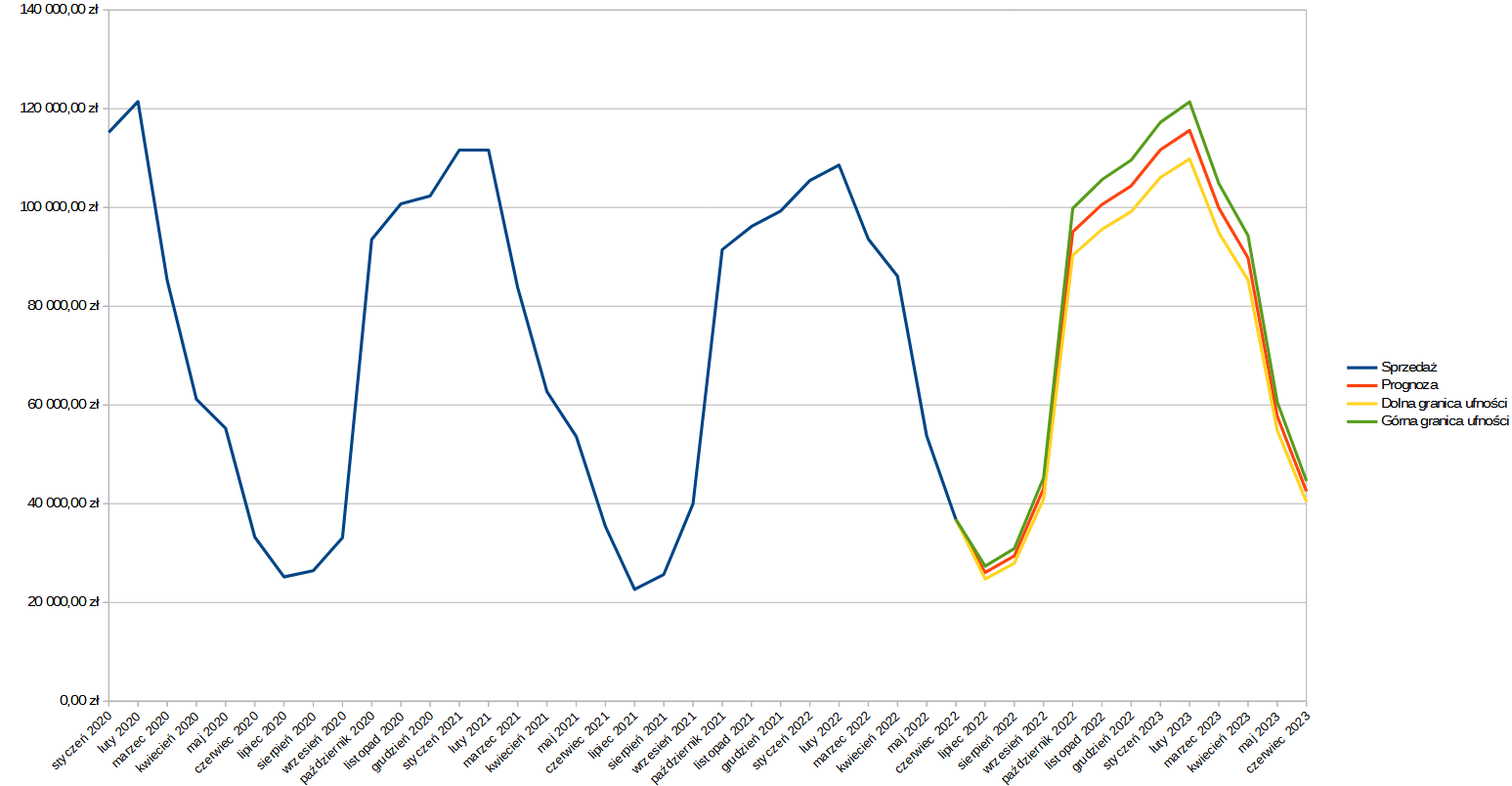
Jak widać, dotychczasowe wyniki firmy były mocno uzależnione od pory roku. W miesiącach zimowych, tj. od października do lutego, można zaobserwować wyraźny wzrost sprzedaży i wynajmu sprzętu narciarskiego. W pozostałym okresie sprzedaż jest zdecydowanie niższa. Taki trend ma również odzwierciedlenie w prognozie, która na podstawie historycznych danych pokazuje, że w kolejnych dwunastu miesiącach istnieje bardzo duże prawdopodobieństwo, że ten trend zostanie utrzymany, a więc firma może spodziewać się w tych miesiącach większego popytu na swoje towary i usługi. Wykonana w ten sposób prognoza pozwala zarządzającym firmą nie tylko oszacować przyszłe zyski, lecz również pokazuje, na jakie stany magazynowe należy się przygotować w kolejnych miesiącach.
Słownik
będący wynikiem sumowania składników