Przeczytaj
Jeśli , to funkcja kwadratowafunkcja kwadratowa przyjmuje wartość najmniejszą dla .
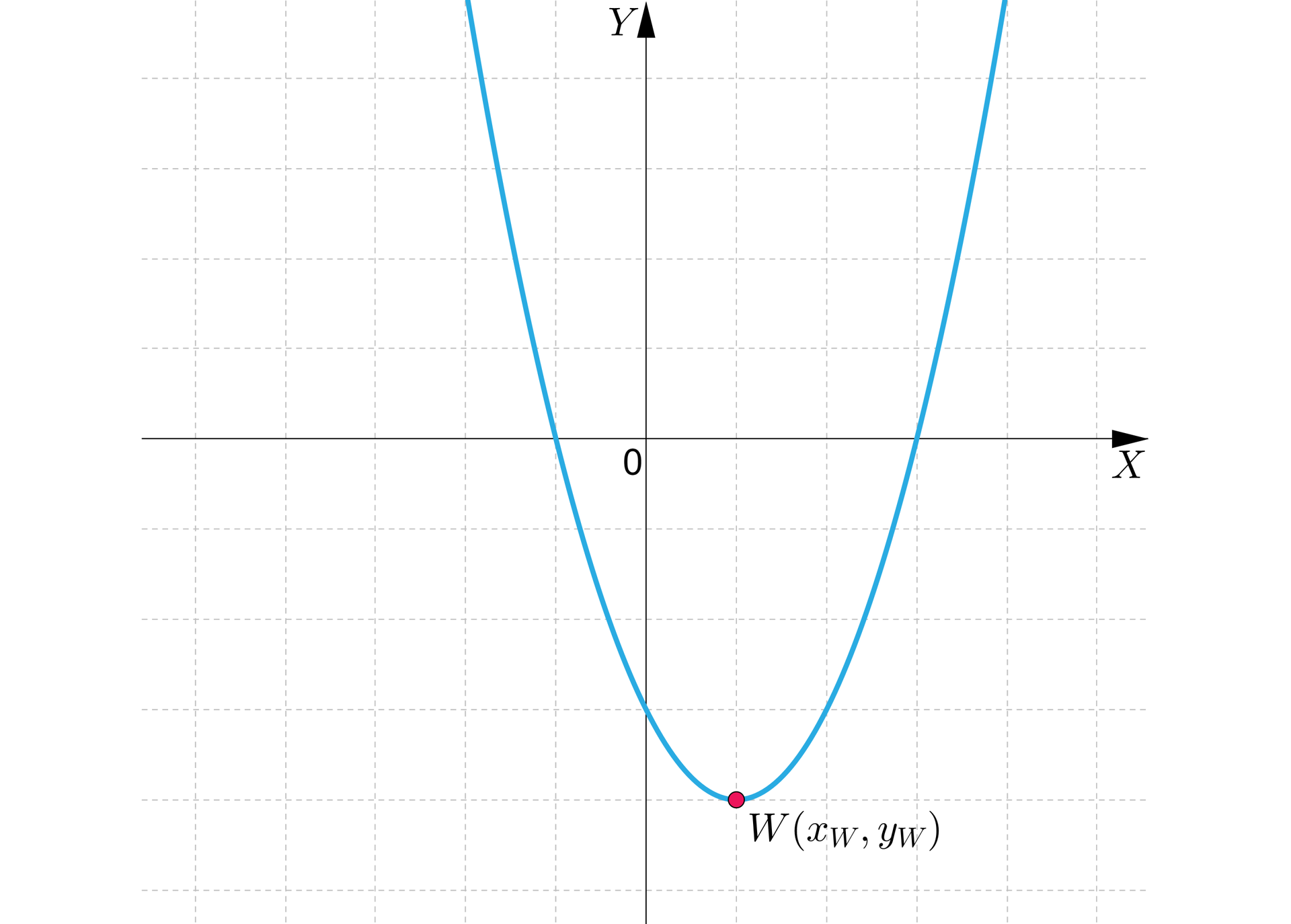
Jeśli , to funkcja przyjmuje wartość największą dla .
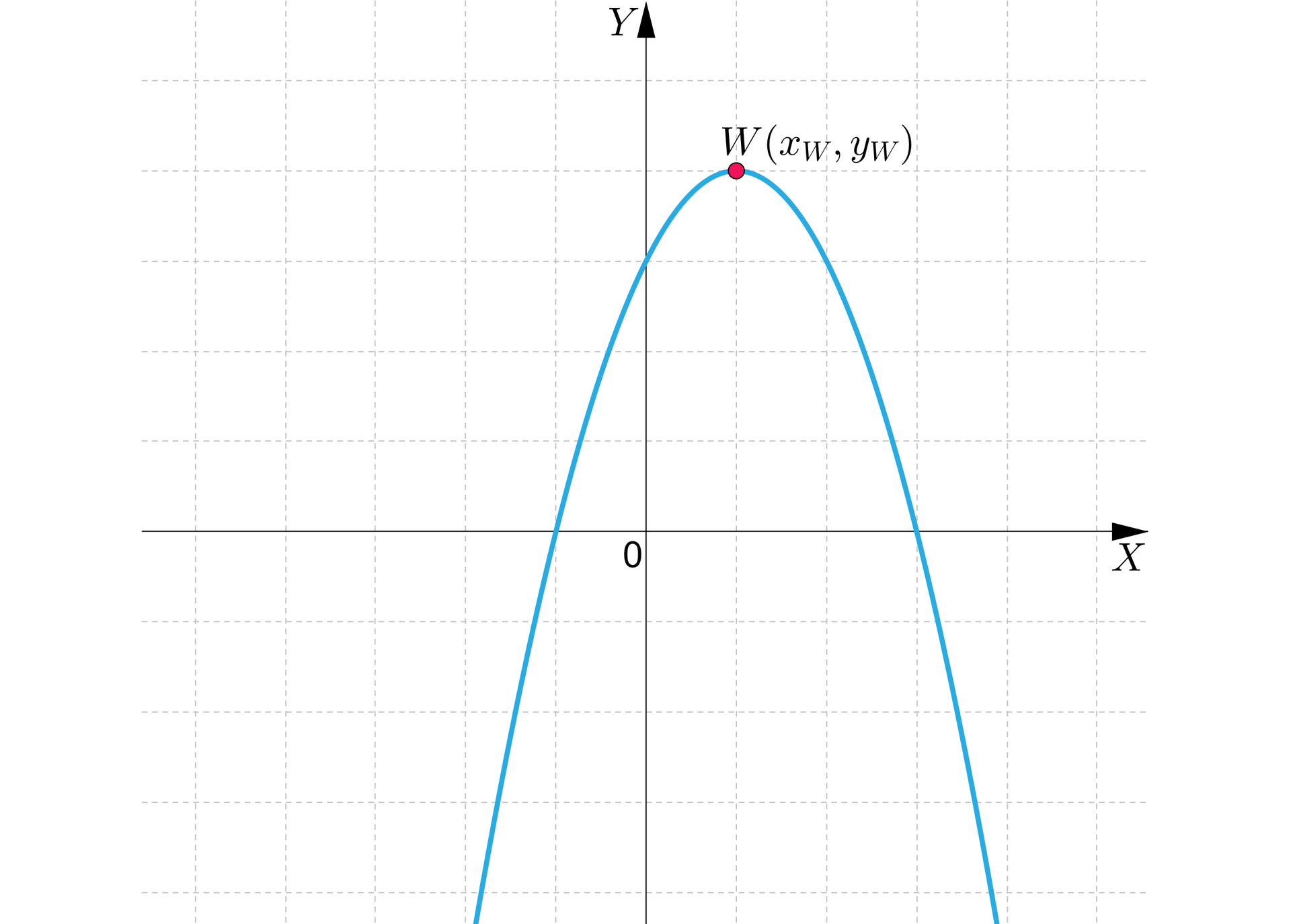
Istnienie najmniejszej lub największej wartości funkcji kwadratowej zależy od współczynnika .
Wykres funkcji kwadratowej możemy wykorzystać do prostych optymalizacji, szukając największej lub najmniejszej wartości danej funkcji. Aby rozwiązać zadanie optymalizacyjne należy wyznaczyć wzór funkcji opisującej sytuację z zadania oraz dziedzinę tej funkcji. Następnie należy znaleźć współrzędne wierzchołka wykresu otrzymanej funkcji kwadratowej.
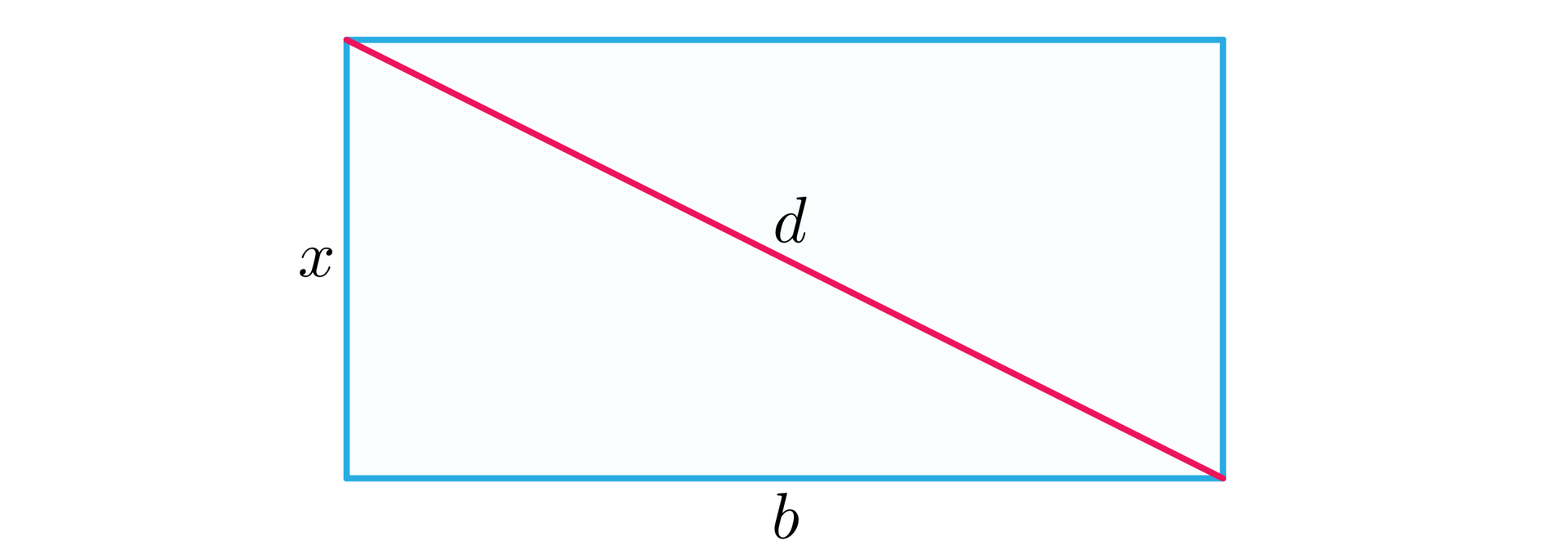
Jakie wymiary ma prostokąt o obwodzie , który ma najkrótszą przekątną?
Rozwiązanie
– przekątna prostokąta
Szukamy boków prostokąta i , dla których przekątna będzie najkrótsza.
Wiemy, że obwód prostokąta wynosi oraz wiemy, że .
.
Długości boków są liczbami dodatnimi: oraz .
.
Zatem w powyższych obliczeń wynika, że i , więc .
Z twierdzenia Pitagorasa mamy, że dlugość przekątnej w prostokącie jest równa: .
.
Przekształcamy wyrażenie podpierwiastkowe do postaci kanonicznejpostaci kanonicznej.
dla każdego .
Otrzymaliśmy wzór funkcji , której wartością jest długość przekątnej prostokąta, w zależności od długości jego boków.
Wykresem funkcji znajdującej się pod pierwiastkiem jest fragment paraboli skierowanej ramionami do góry , więc dla wierzchołka przyjmuje wartość najmniejszą.
Współrzędne wierzchołka paraboli to:
, oraz .
Dla wyrażenie podpierwiastkowe przyjmuje wartość najmniejszą równą .
Przekątna będzie najkrótsza, gdy wyrażenie podpierwiastkowe będzie najmniejsze, czyli dla . Długość przekątnej wynosi w tym przypadku .
Prostokąt ma boki o długościach: i , czyli jest to kwadrat o boku długości .
Odpowiedź
Najkrótszą przekątną ma kwadrat o boku .
Który z walców o obwodzie przekroju osiowego równym ma największe pole powierzchni bocznej?
Rozwiązanie
Przekrojem osiowym walca jest prostokąt o bokach: (wysokość walca) i ( to promień podstawy walca).
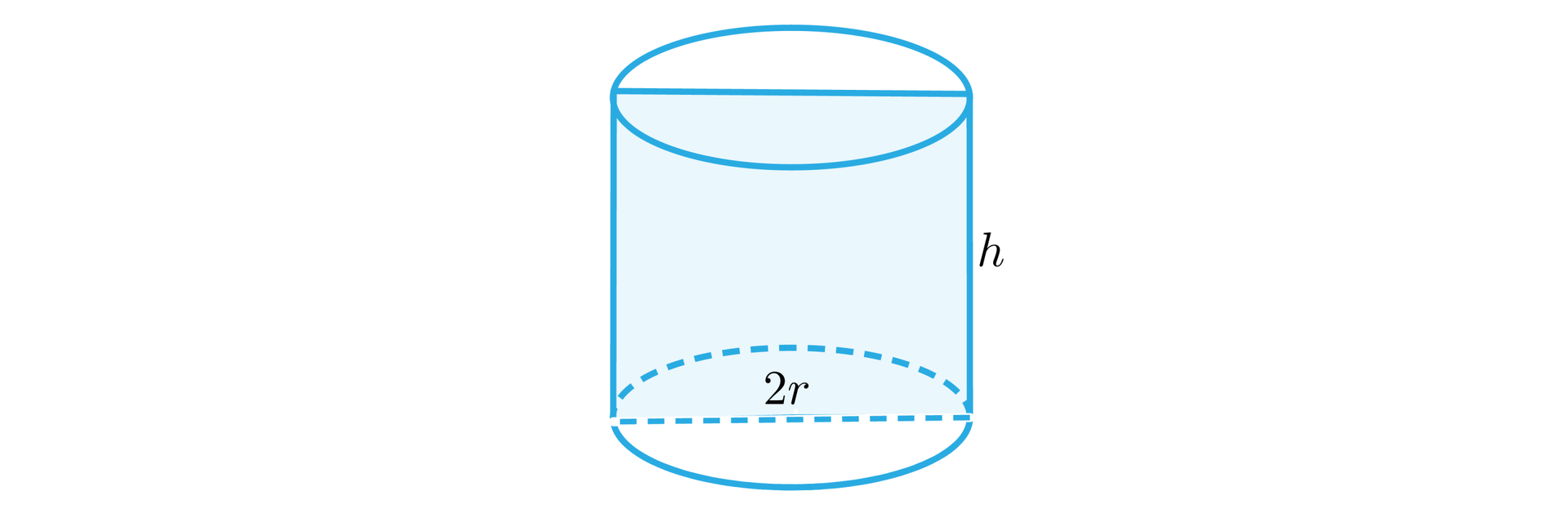
Obwód prostokąta będącego przekrojem osiowym walca wyraża wzór:
.
Oznaczmy przez promień podstawy walca.
Podstawmy dane.
.
Po podzieleniu stronami przez , otrzymujemy:
.
Stąd .
Długości boków są liczbami dodatnimi, więc oraz .
.
Zauważmy, że oraz jednocześnie , zatem mamy, że .
Przypomnijmy, że pole powierzchni bocznej walca wyraża wzór: .
dla .
Otrzymaliśmy funkcję wyrażoną wzorem: .
Ponieważ , to funkcja dla wierzchołka przyjmuje wartość największą. Aby wyliczyć współrzędne wierzchołka, wykorzystamy fakt, że funkcja jest przedstawiona w postaci iloczynowej. Pierwsza współrzędna wierzchołka jest średnią arytmetyczną miejsc zerowych funkcji kwadratowej.
.
Zatem .
Obliczmy wysokość walca.
Odpowiedź
Walec, którego promień podstawy wynosi i wysokość ma największe pole powierzchni bocznej wynoszące .
Suma długości wysokości i obu podstaw trapezu równoramiennego wynosi . Oblicz długość przekątnej tego trapezu, gdy trapez ma pole największe z możliwych.
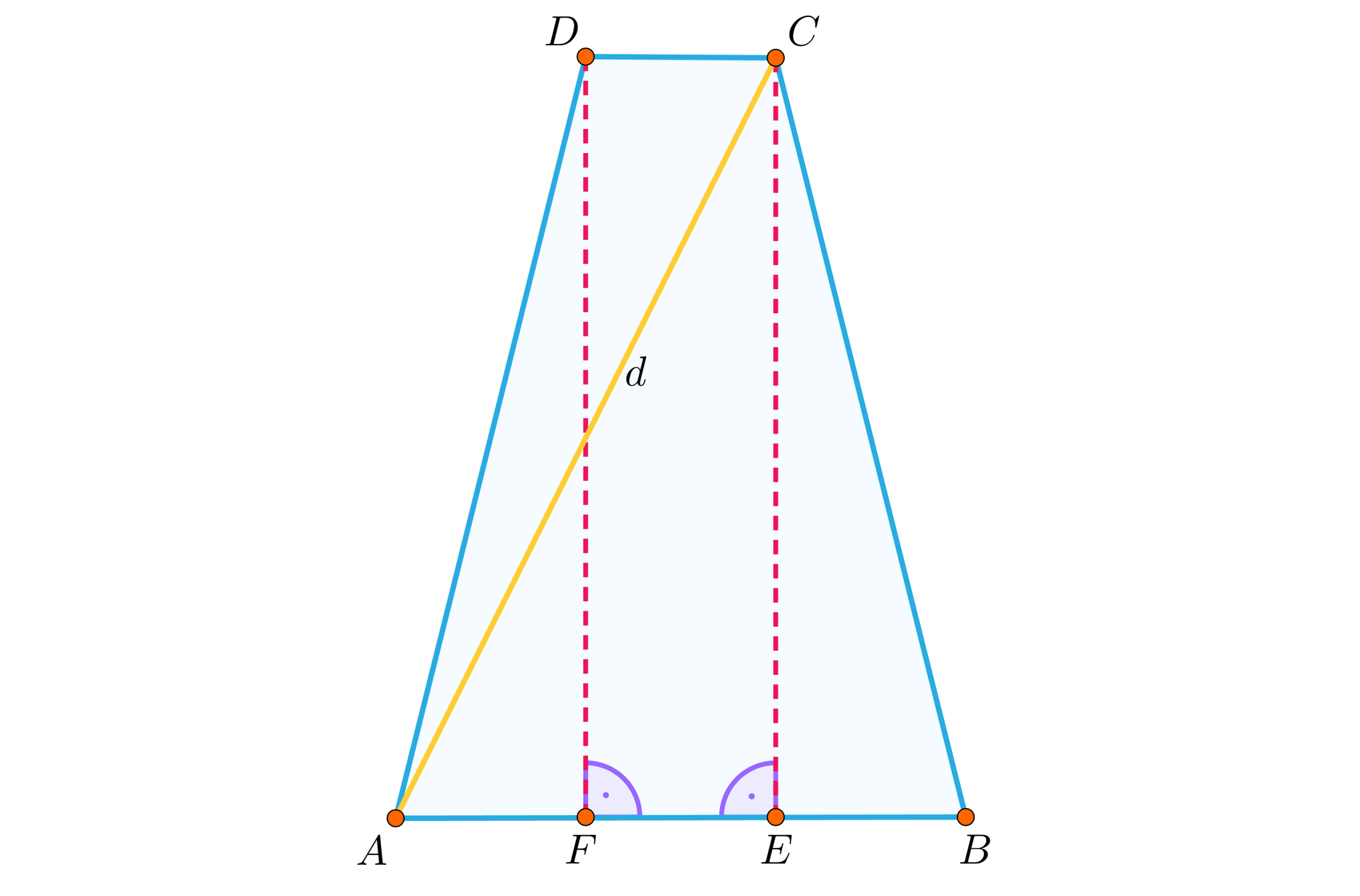
Rozwiązanie
Oznaczmy: .
Z treści zadania wiemy, że .
Oznaczmy .
Otrzymamy więc, że .
Stąd .
Długości boków są dodatnie: oraz , stąd .
Pole trapezu wyraża wzór: .
Wzór szukanej funkcji to , przy czym .
Funkcja jest zapisana w postaci iloczynowej. Jej miejscami zerowymi są liczby i . Ponieważ , funkcja w wierzchołku przyjmuje wartość największą, a współrzędna wierzchołka jest średnią arytmetyczną miejsc zerowych odpowiedniej funkcji kwadratowej.
.
Zatem dla pole przyjmuje wartość największą.
Obliczmy wysokość trapezu z poniższego wzoru.
Aby obliczyć długość przekątnej tego trapezu, skorzystamy z twierdzenia Pitagorasa zapisanego dla trójkąta prostokątnego , mianowicie: .
Przyjmijmy oznaczenia:
– przekątna trapezu,
– wysokość trapezu.
Z rysunku wynika, że .
Zauważmy, że, ponieważ trapez jest równoramienny. Mamy więc, że oraz .
Ponieważ , mamy
.
Zatem oraz . Podstawmy obliczone wartości do poniższego wzoru.
Odpowiedź
Długość przekątnej trapezu o największym polu wynosi .
Drut o długości dzielimy na dwie części. Z jednej tworzymy kwadrat, z drugiej prostokąt, w którym stosunek długości boków wynosi . Na jakie części trzeba rozciąć drut, aby suma pól kwadratu i prostokąta była najmniejsza?
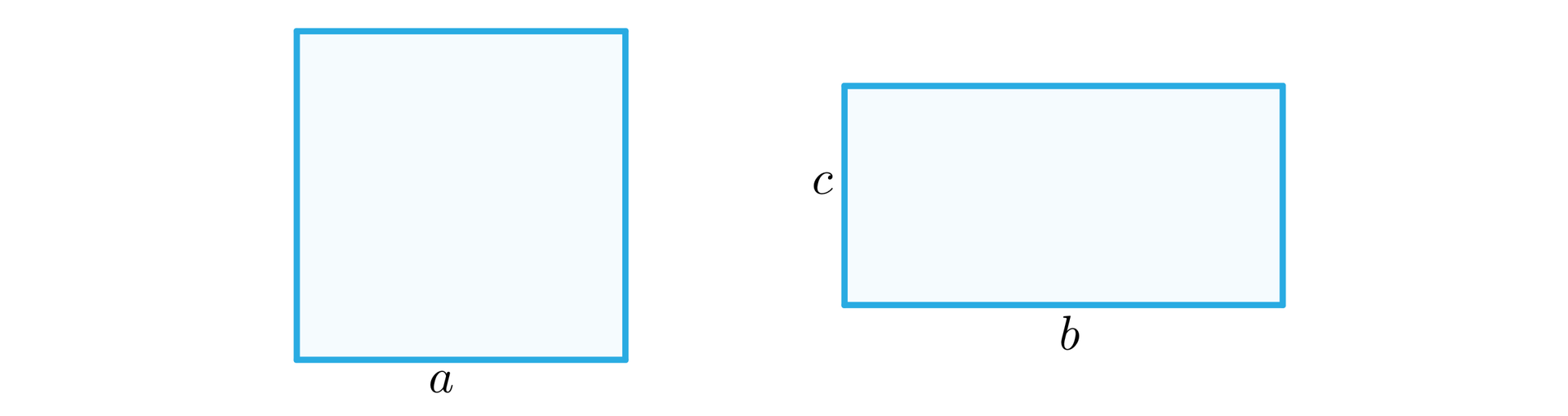
Korzystając z powyższych rysunków dostajemy, że:
obwód kwadratu: ;
obwód prostokąta: .
Stosunek długości boków prostokąta wynosi , więc oraz .
Z treści zadania wynika, że suma obwodów kwadratu i prostokąta jest równa długości drutu.
– długość drutu.
Z powyższych rozważań oraz z treści zadania mamy więc, że .
Z powyższego równania wyznaczmy .
.
Pole kwadratu: .
Pole prostokąta: .
Suma pól kwadratu i prostokąta: .
Możemy zapisać powyższy wzór na pole jako wzór funkcji.
.
Ponieważ długości boków nie mogą być ujemne, muszą być spełnione warunki:
oraz .
oraz , zatem .
Otrzymaliśmy funkcję wyrażoną wzorem . Ponieważ , funkcja w wierzchołku wykresu przyjmuje wartość najmniejszą. Aby obliczyć współrzędne wierzchołka, wykorzystamy poniższy wzór.
.
Funkcja przyjmuje wartość najmniejszą dla , .
.
Odpowiedź
Drut należy przeciąć na dwie części o długościach: oraz .
Z trójkąta , w którym , należy wyciąć równoległobok, którego jeden bok byłby zawarty w podstawie , a drugi – w jednym z pozostałych boków trójkąta i który miałby największe pole. Oblicz długości boków i pole szukanego równoległoboku.
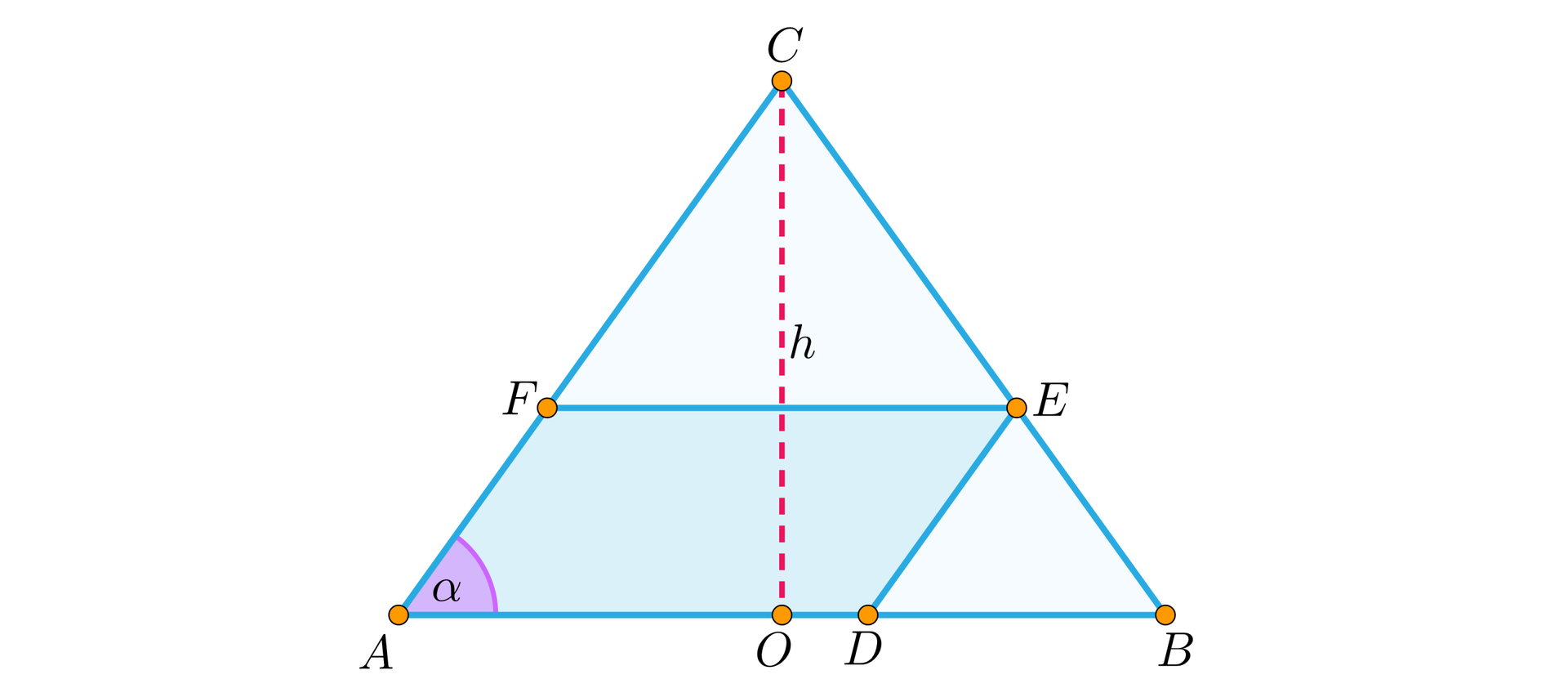
Czworokąt jest równoległobokiem, oznaczmy oraz .
Trójkąt jest podobny do trójkąta – trójkąty mają takie same kąty.
.
Z cechy wiemy, że odpowiednie odcinki są proporcjonalne:
oraz .
.
Długości boków spełniają warunki:
oraz
.
Zatem mamy, że oraz , więc .
Pole równoległoboku wyraża wzór: , co możemy też zapisać za pomocą przyjętych oznaczeń: .
.
Wysokość trójkąta wyliczymy z twierdzenia Pitagorasa zapisanego poniżej dla trójkąta prostokątnego .
, ponieważ trójkąt jest równoramienny.
Stąd .
Zatem .
Pole równoległoboku wyraża wzór: , gdzie .
Funkcja przyjmuje wartość największą w wierzchołku paraboli będącej wykresem funkcji , ponieważ .
Funkcja zapisana jest w postaci iloczynowej. Skorzystamy z faktu, że pierwsza współrzędna wierzchołka paraboli jest średnią arytmetyczną jej miejsc zerowych. Miejsca zerowe funkcji to oraz .
, .
Maksymalne pole jest równe: .
.
Odpowiedź
Długości boków szukanego równoległoboku wynoszą: i , a jego pole wynosi .
Słownik
funkcję określoną dla wszystkich liczb rzeczywistych , gdzie są liczbami rzeczywistymi, przy czym , nazywamy funkcją kwadratową; jej wykresem jest parabola
,