Przeczytaj
Przypomnijmy definicję kąta dwuściennego.
Dane są dwie półpłaszczyzny o wspólnej krawędzi, które dzielą przestrzeń na dwie części.
Kątem dwuściennym nazywamy sumę dwóch półpłaszczyzn o wspólnej krawędzi i jednego z dwóch obszarów, które te półpłaszczyzny wycinają z przestrzeni.
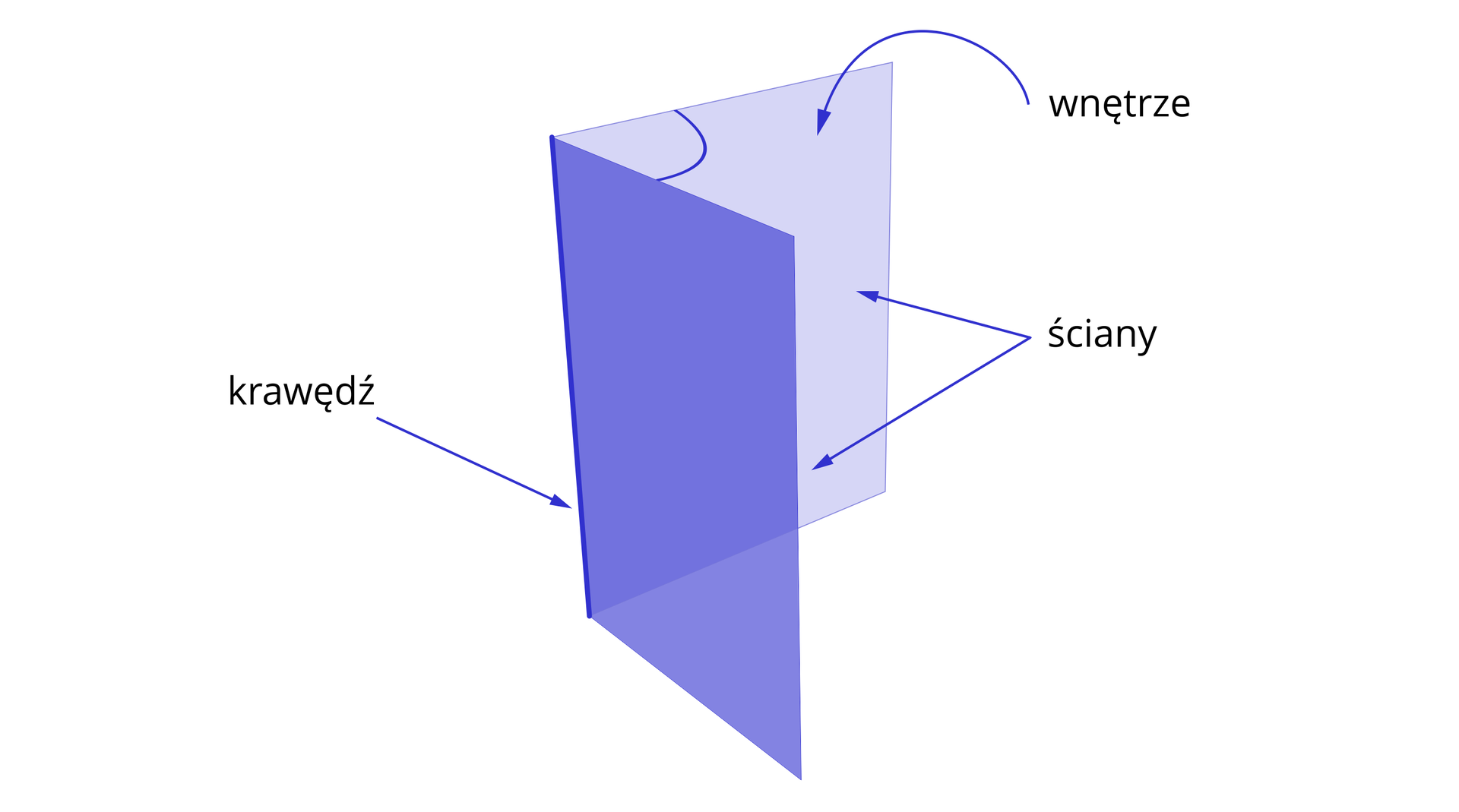
Wspólną krawędź półpłaszczyzn nazywamy krawędzią kąta dwuściennego, a półpłaszczyzny – ścianami kąta dwuściennego.
Wprowadźmy definicję miary liniowej kąta dwuściennego.
Miarą liniową kąta dwuściennego nazywamy miarę kąta płaskiego, będącego częścią wspólną tego kąta dwuściennego oraz płaszczyzny prostopadłej do jego krawędzi.
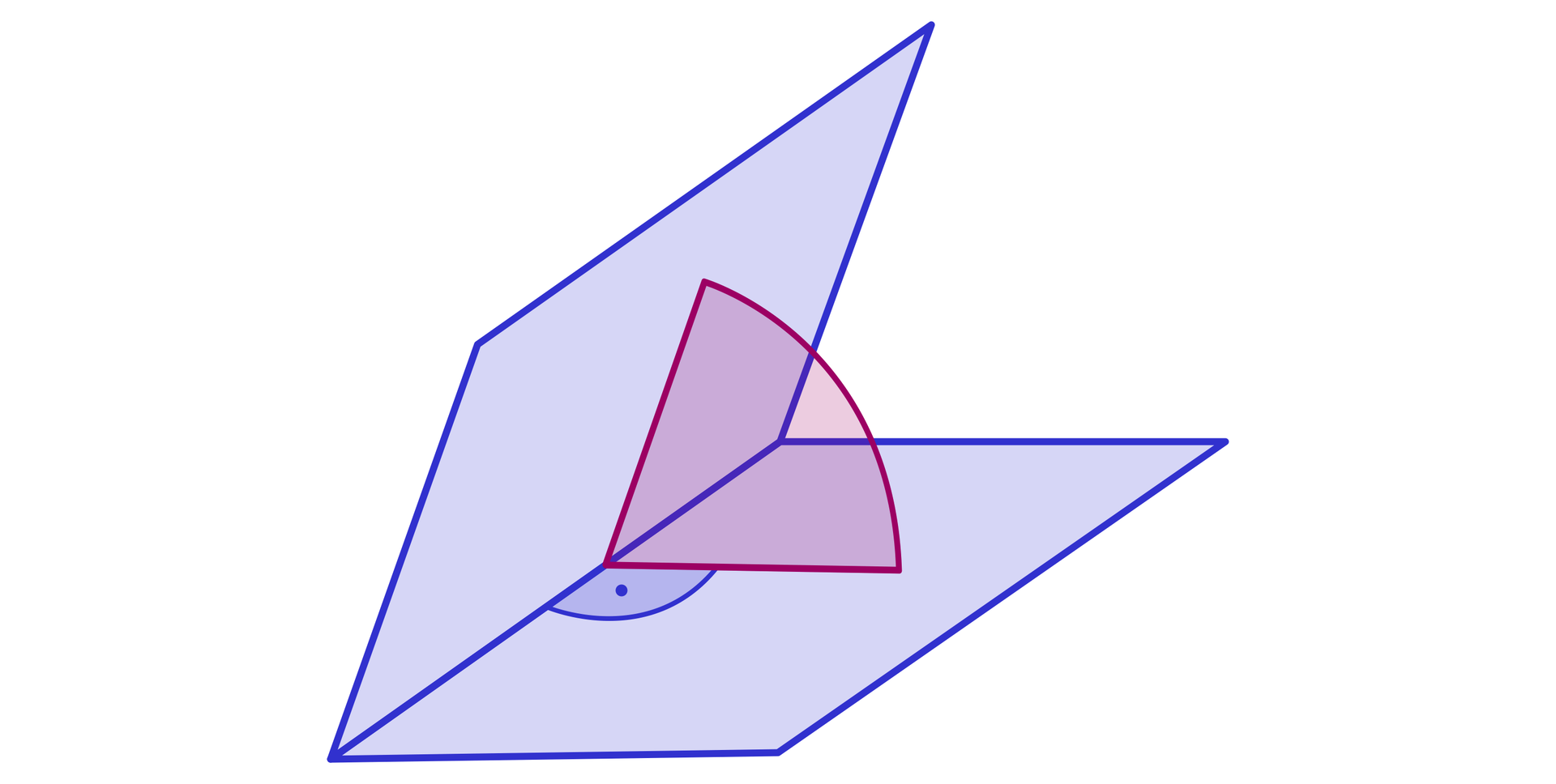
Wyznaczanie miary liniowej kąta dwuściennego przebiega w kolejnych krokach.
Najpierw szukamy ścian, pomiędzy którymi wyznaczymy miarę liniową kąta (mogą to być np. ściany boczne w graniastosłupie, ściana boczna graniastosłupa oraz jego podstawa, ściana boczna ostrosłupa oraz jego podstawa, itp.).
Jeżeli ściany się przecinają, to wskazujemy prostą, powstałą poprzez przecięcie tych ścian.
Na obu ścianach wyróżniamy proste (półproste) prostopadłe do wskazanej prostej.
Miara liniowa kąta dwuściennego jest równa mierze kąta płaskiego pomiędzy tymi prostymi.
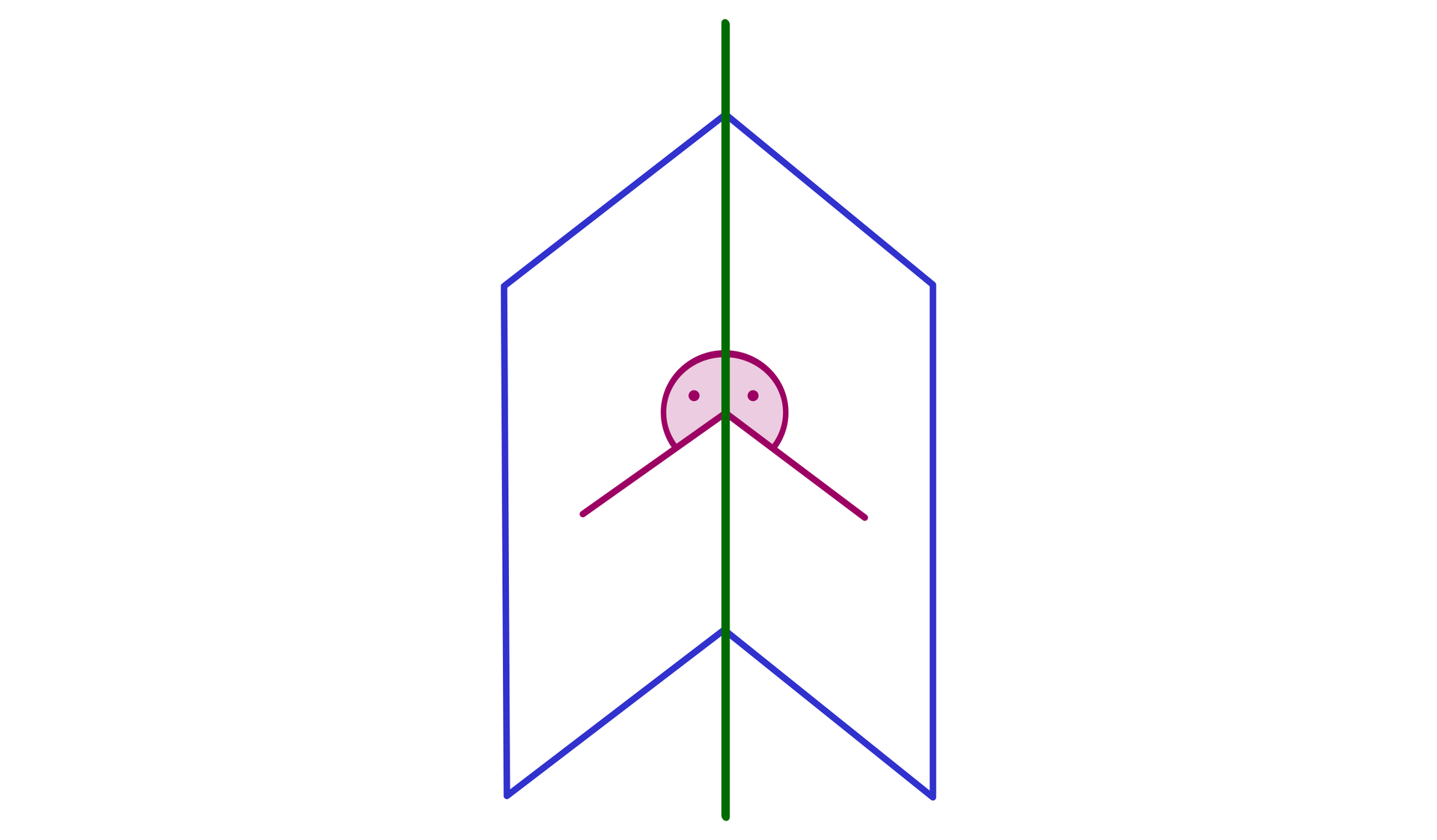
Zauważmy, że w graniastosłupie prostym ściany boczne są prostopadłeprostopadłe do podstaw, zatem miara liniowa kąta dwuściennego między tymi ścianami wynosi .
Dany jest graniastosłup prosty jak na rysunku, którego podstawą jest trójkąt prostokątny o przyprostokątnych długości i . Obliczymy miary kątów między ścianami bocznymi tego graniastosłupa.

Rozwiązanie:
Ponieważ kąt jest prosty, zatem kąt pomiędzy ścianami i również jest prosty.
Wyznaczmy miary liniowe pozostałych kątów. W tym celu rozpatrzmy trójkąt prostokątny, jak na poniższym rysunku.
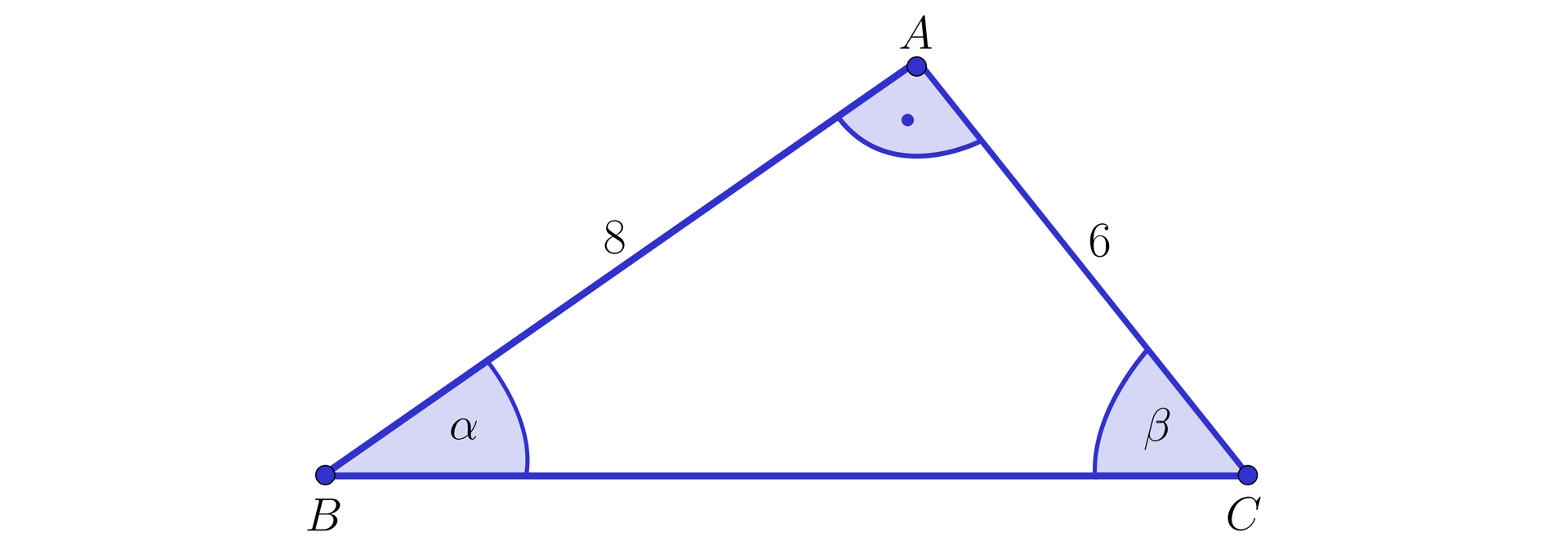
Korzystając z funkcji trygonometrycznej tangens mamy:
Korzystając z tablic wartości funkcji trygonometrycznych odczytujemy, że .
Wobec tego .
Miara kąta jest taka sama, jak miara kąta liniowego pomiędzy ścianami i , zatem szukany kąt wynosi około .
Miara kąta jest taka sama, jak miara kąta liniowego pomiędzy ścianami i , zatem szukany kąt wynosi około .
Wyznaczymy miarę liniową kąta dwuściennego pomiędzy sąsiednimi ścianami bocznymi w graniastosłupie prawidłowym ośmiokątnym.
Rozwiązanie:
Narysujmy graniastosłup prawidłowy ośmiokątny.
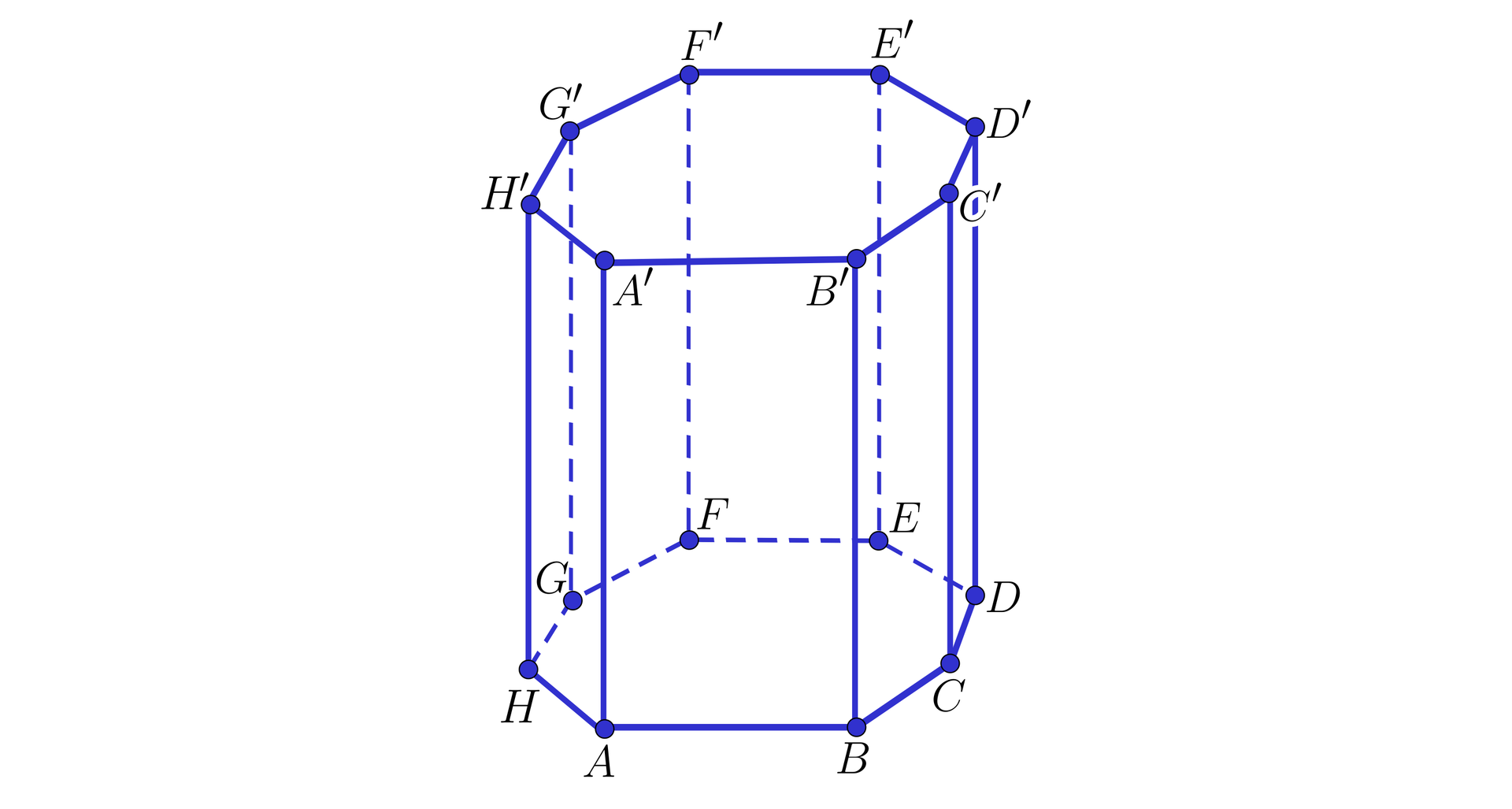
Ponieważ podstawą graniastosłupa jest wielokąt foremny, to miara liniowa kąta dwuściennego między ścianami bocznymi tego graniastosłupa będzie taka sama.
Wystarczy zatem wyznaczyć miarę kąta pomiędzy sąsiednimi krawędziamikrawędziami w podstawie ośmiokąta foremnego. W tym celu narysujmy ośmiokąt foremny i wprowadźmy oznaczenia, jak na rysunku:
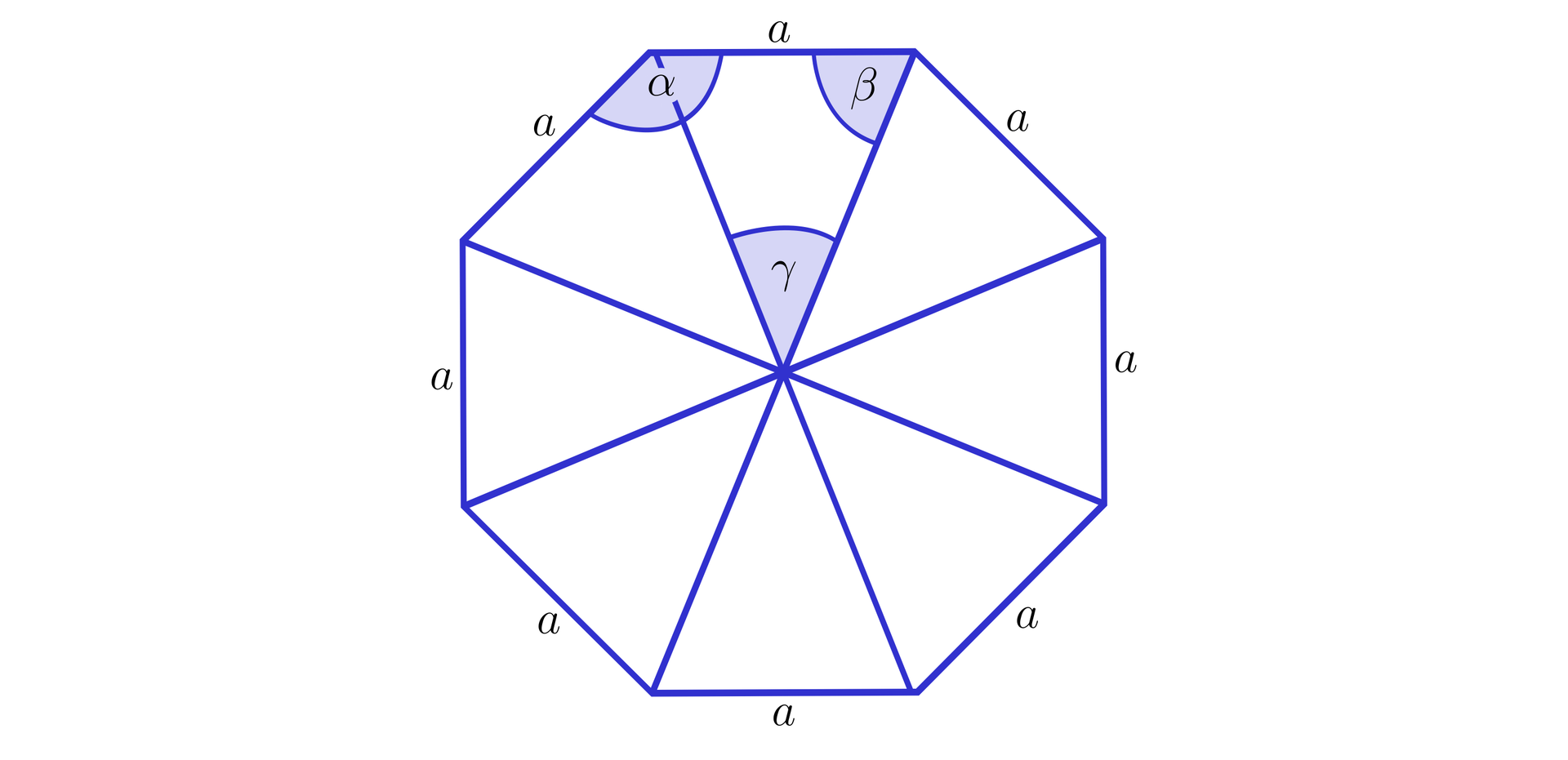
Mamy:
Zatem miara liniowa kąta dwuściennego pomiędzy sąsiednimi ścianami bocznymi w graniastosłupie prawidłowym ośmiokątnym wynosi .
Miara liniowa kąta dwuściennego jest równa . Na jednej ze ścian leży punkt , którego odległość od drugiej ściany jest równa . Obliczymy odległość punktu od krawędzi kąta dwuściennego.
Rozwiązanie:
Narysujmy rysunek pomocniczy do zadania i wprowadźmy odpowiednie oznaczenia.
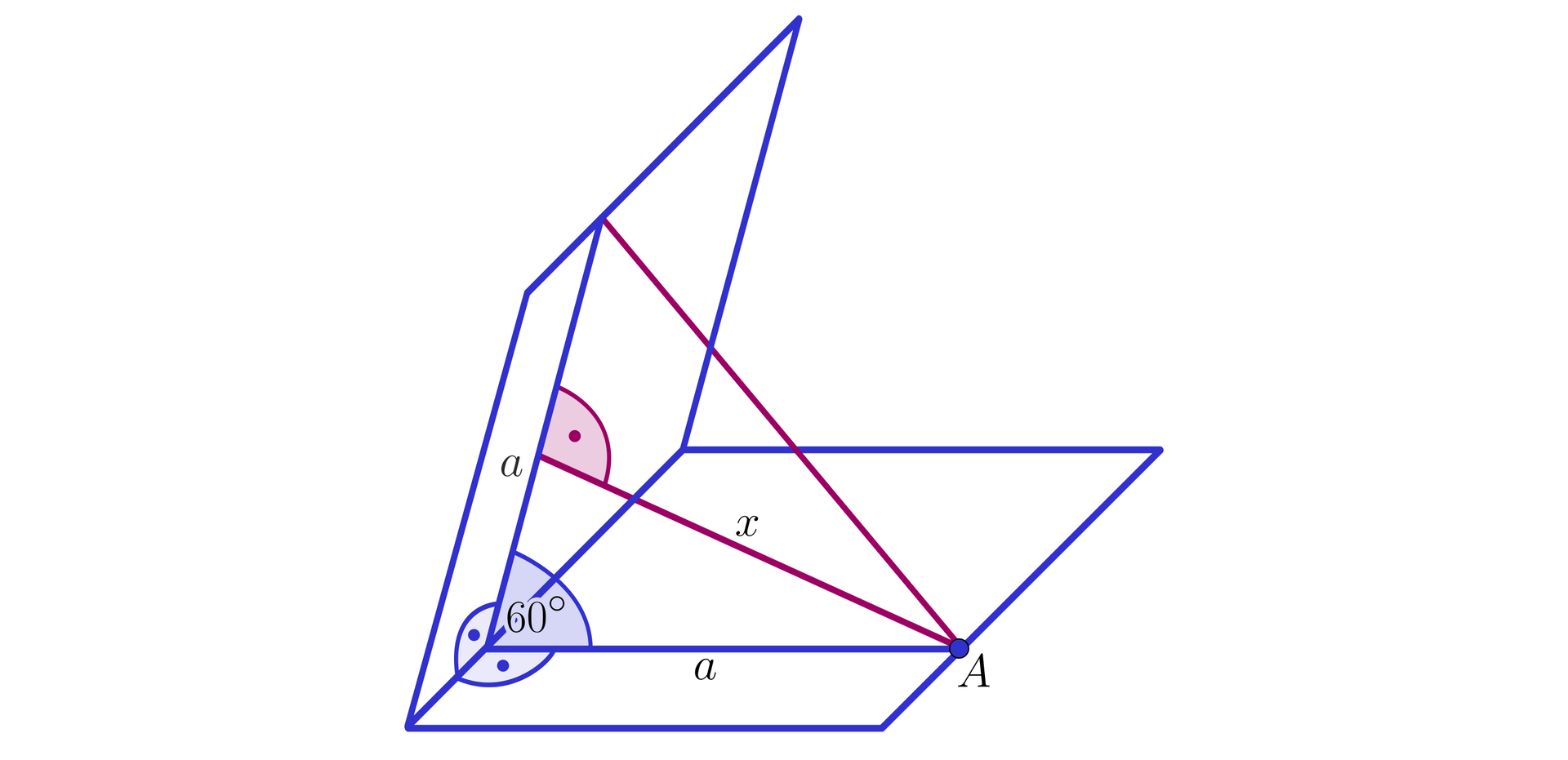
Zauważmy, że do wyznaczenia odległości punktu od krawędzi kąta dwuściennego wystarczy rozpatrzeć trójkąt, jak na poniższym rysunku.
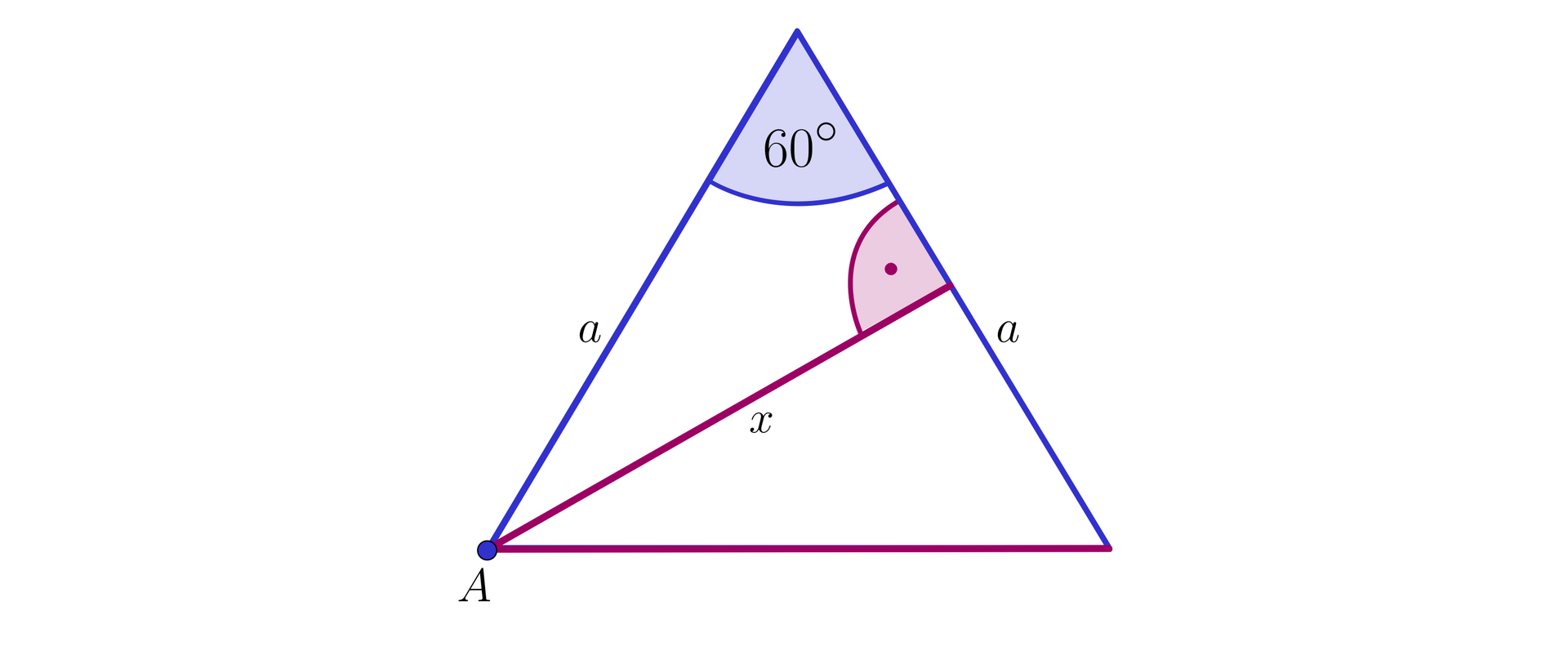
Z treści zadania wynika, że .
Otrzymany trójkąt jest równoboczny, a długość odcinka jest równa jego wysokości.
Jeżeli jest długością boku trójkąta równobocznego i szukaną odległością, to do wyznaczenia wartości rozwiązujemy równanie:
Wobec tego .
Zatem szukana odległość wynosi .
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakowe długości. Obliczymy cosinus kąta dwuściennego między sąsiednimi ścianami bocznymi tego ostrosłupa.
Rozwiązanie:
Narysujmy ostrosłup prawidłowy czworokątny i wprowadźmy oznaczenia, jak na rysunku.
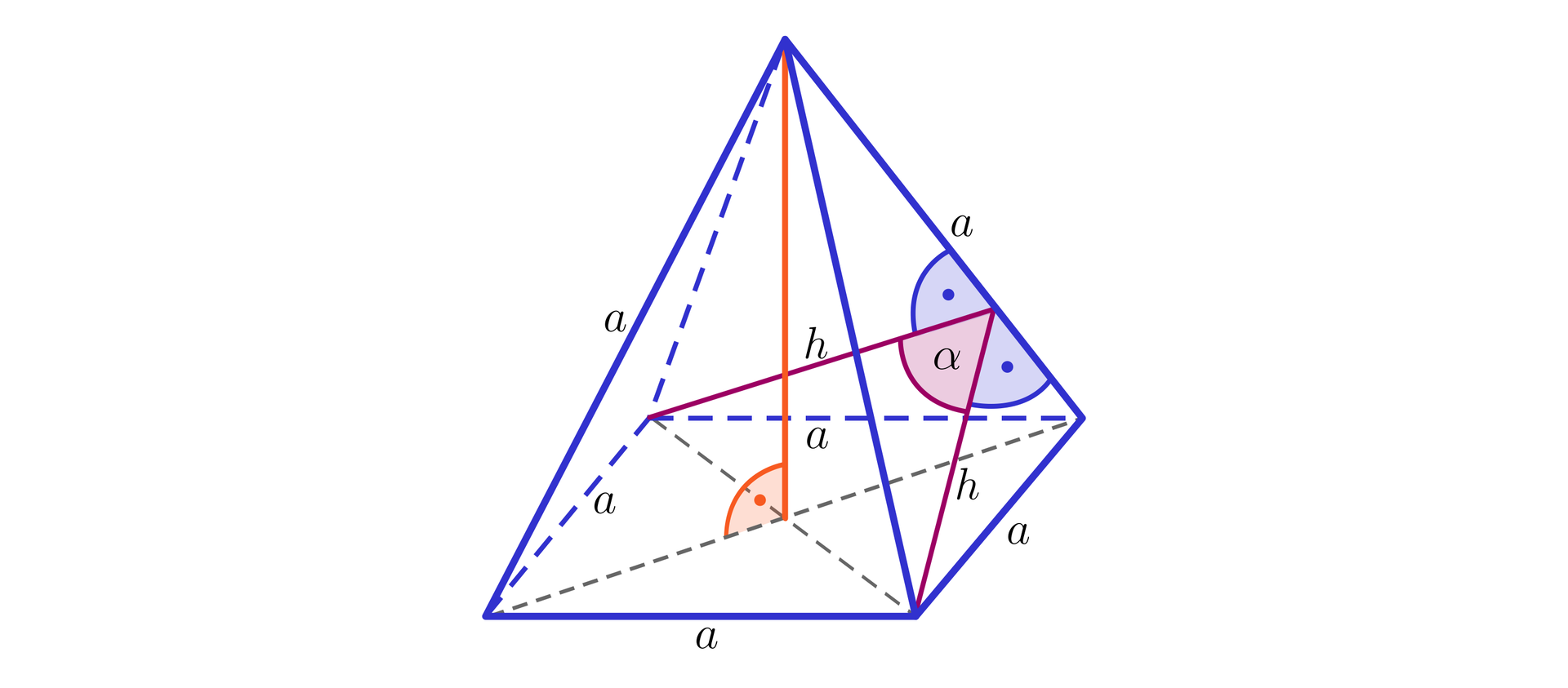
Ponieważ ściany boczne tego ostrosłupa są trójkątami równobocznymi, to:
Wobec tego do wyznaczenia miary kąta korzystamy z trójkąta równoramiennego, jak na poniższym rysunku.
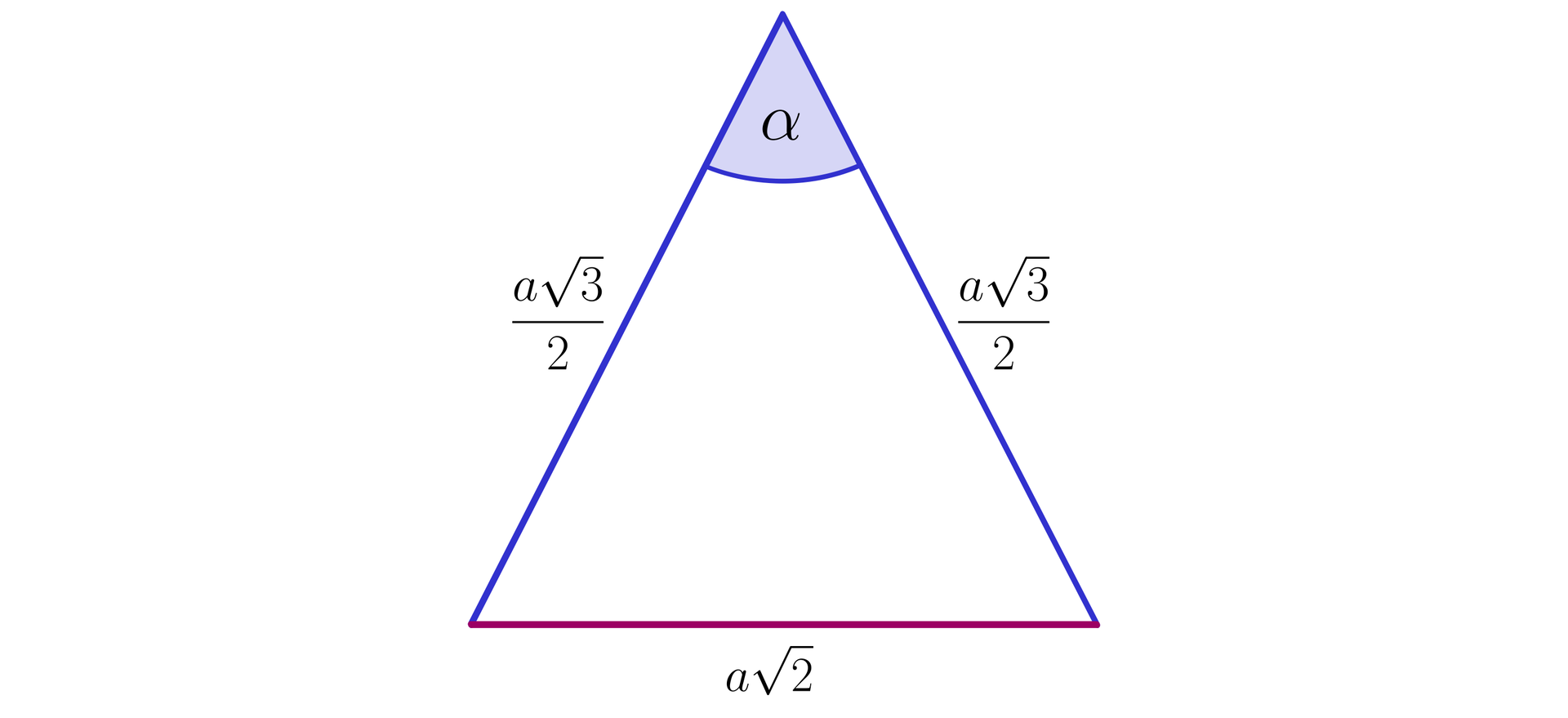
Rozwiązujemy równanie, korzystając z twierdzenia cosinusów:twierdzenia cosinusów:
Zatem .
W graniastosłupie prawidłowym czworokątnym poprowadzono płaszczyznę, jak na poniższym rysunku. Obliczymy miarę liniową kąta dwuściennego pomiędzy tą płaszczyzną i płaszczyzną podstawy graniastosłupa.
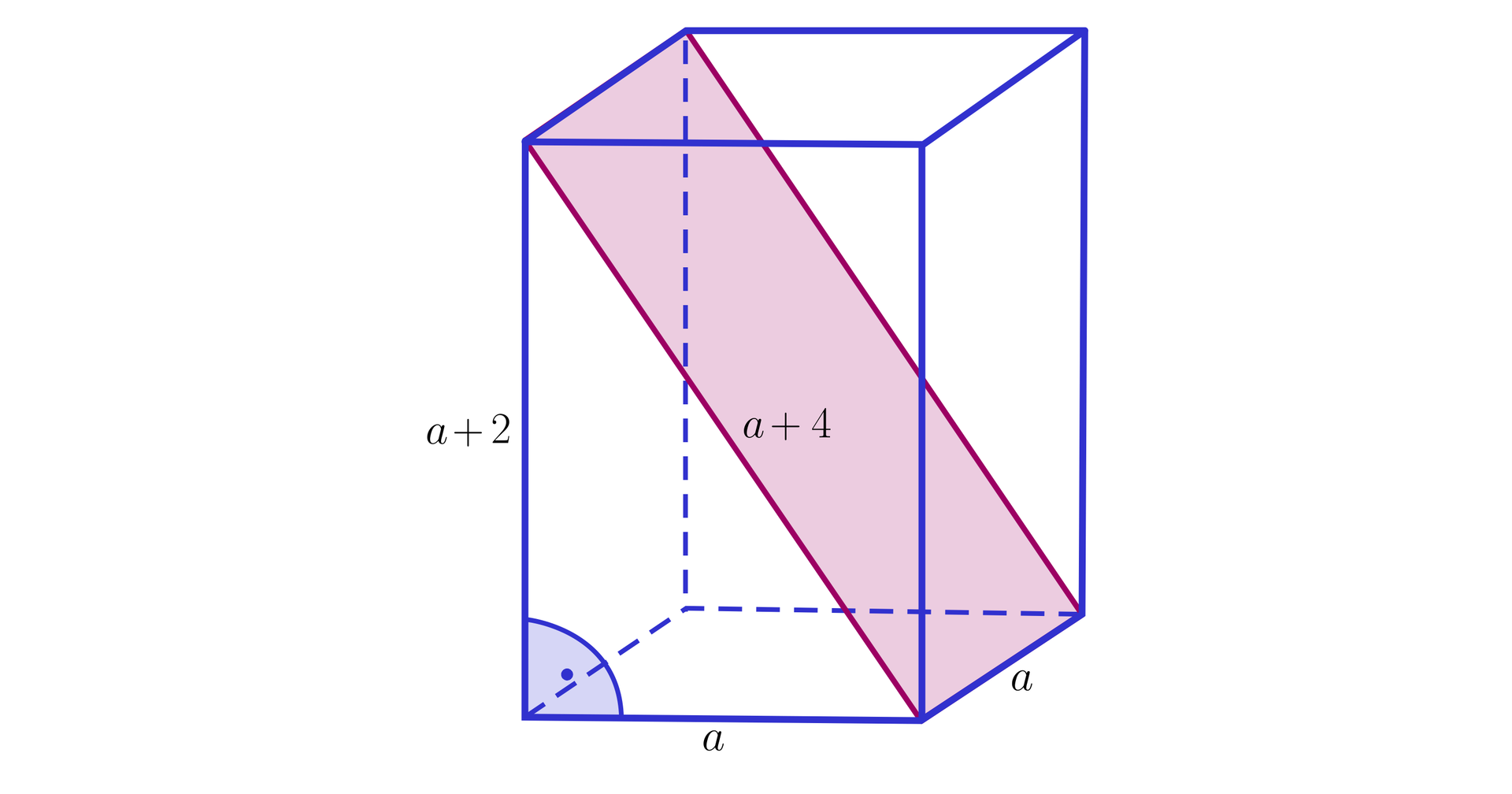
Rozwiązanie:
Do wyznaczenia wartości rozwiązujemy równanie, korzystając z twierdzenia Pitagorasa.
Zatem:
Niech będzie miarą liniową rozpatrywanego kąta.
Do wyznaczenia tej miary wystarczy rozpatrzeć trójkąt prostokątny, jak na poniższym rysunku.
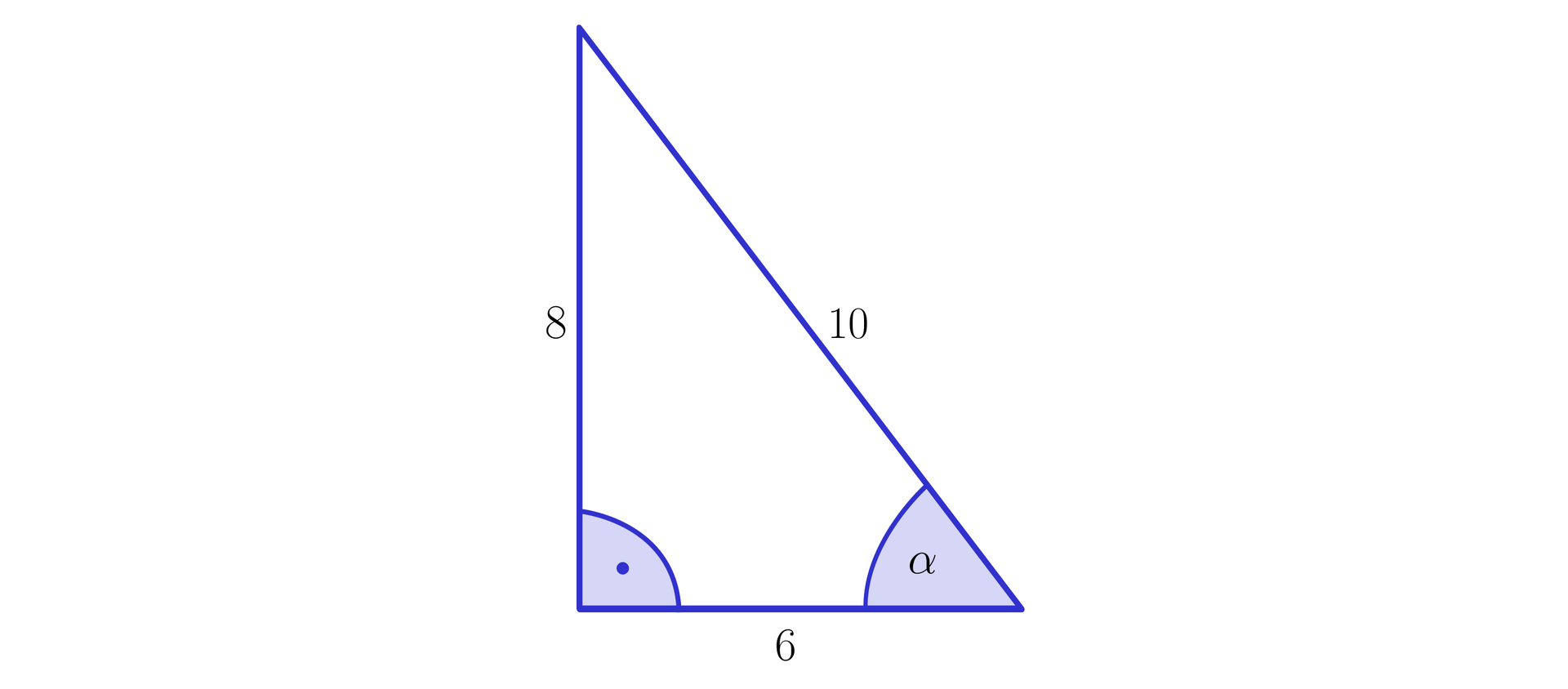
Ponieważ , wobec tego miara kąta wynosi około .
Słownik
bok wielokąta, który jest ścianą graniastosłupa
dwie płaszczyzny są prostopadłe, gdy istnieje prosta zawarta w pierwszej płaszczyźnie prostopadła do drugiej płaszczyzny
w dowolnym trójkącie, kwadrat długości dowolnego boku jest równy sumie kwadratów długości pozostałych boków, pomniejszonej o podwojony iloczyn długości tych boków i cosinusa kąta zawartego między nimi