Infografika
Polecenie 1
Zapoznaj się z infografiką, zwróć uwagę, jak zmienia się odległość punktu od krawędzi kąta dwuściennego, gdy dana jest odległość tego punktu od drugiej ściany.
Polecenie 2
Oblicz długości zaznaczonych odcinków w danym kącie dwuściennym na poniższym rysunku.
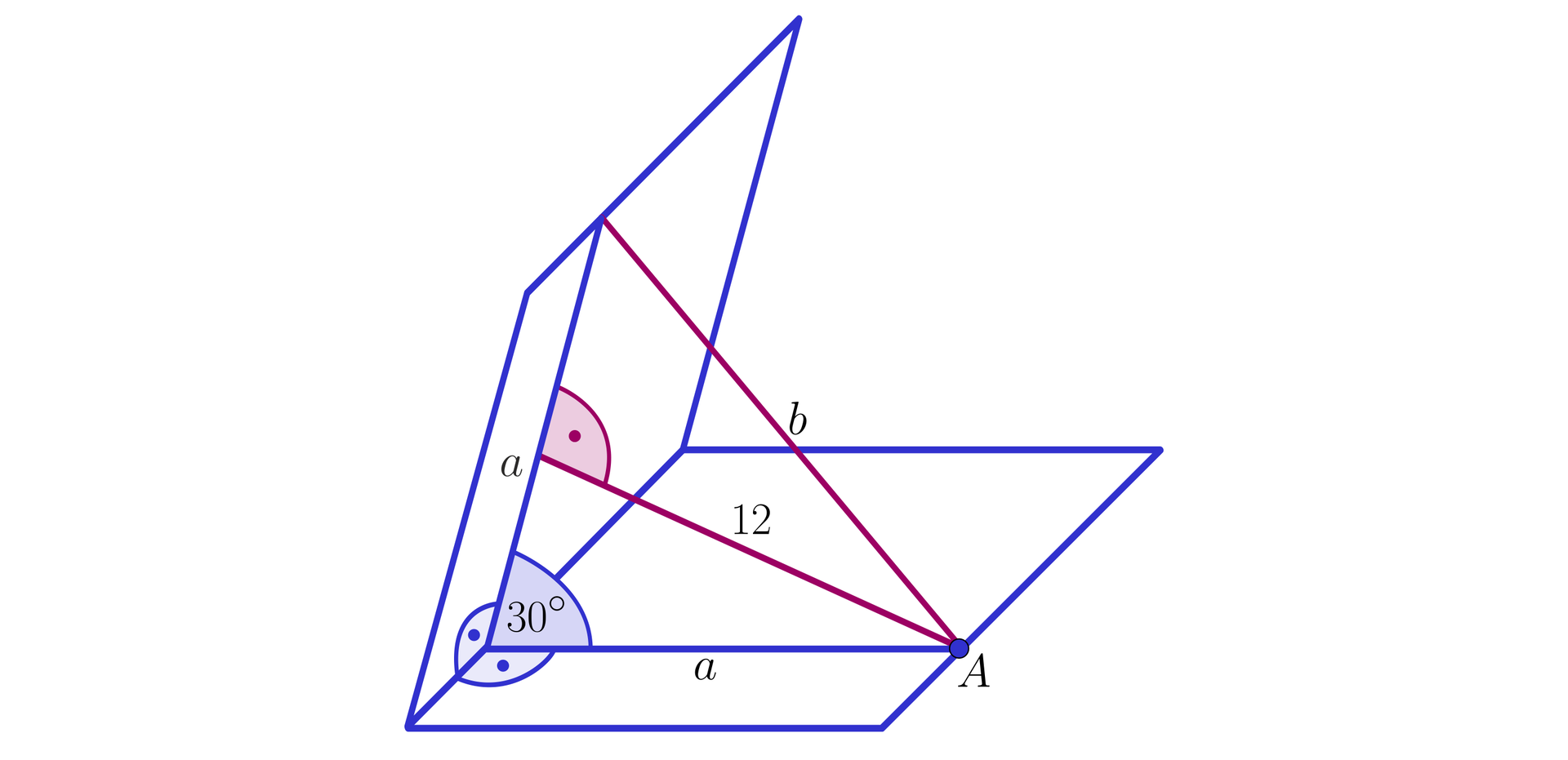
Miara liniowa kąta dwuściennego wynosi . Odcinki tworzące ten kąt mają długość: . Oblicz długośc odcinka , który leży naprzeciw kąta dwuściennego i łączy końce pozostałych odcinków.