Przeczytaj

Zacznijmy od przeanalizowania poniższego rysunku.

RSx549UsSzQ7P

Ilustracja przedstawia okrąg. Punkt O jest środkiem okręgu. Na okręgu zaznaczono dwa punkty A oraz B. Do obu punktów poprowadzono promień z punktu O. Powstał wycinek okręgu o promieniu r oraz długości łuku l.

Przedstawiony został okrąg o promieniu $r$ . Punkty $A$ , $B$ leżące na okręgu tworzą łuk długości $l$ . W jaki sposób możemy policzyć długość owego łuku? Znamy wzór na obwód okręgu – wyraża się on wzorem:

L = 2 π r

Jednakże, my potrzebujemy znać długość tylko pewnego fragmentu tego obwodu. Skorzystamy z faktu, że stosunek kąta środkowegokąt środkowykąta środkowego $∢ A O B$ do kąta pełnegokąt pełnykąta pełnego jest taki sam, jak stosunek długości łuku wycinka koła do długości obwodu koła.

Prawidłowość tę sformułujmy w postaci poniższego twierdzenia:

o długości łuku okręgu

Twierdzenie: o długości łuku okręgu

Dla okręgu o promieniu $r > 0$ długość łuku $l$ opartego na kącie środkowym $α$ wyraża się wzorem:

l = 2 π r \cdot \frac{α}{360 °}

Zacznijmy od rozważenia następującego przykładu:

Przykład 1

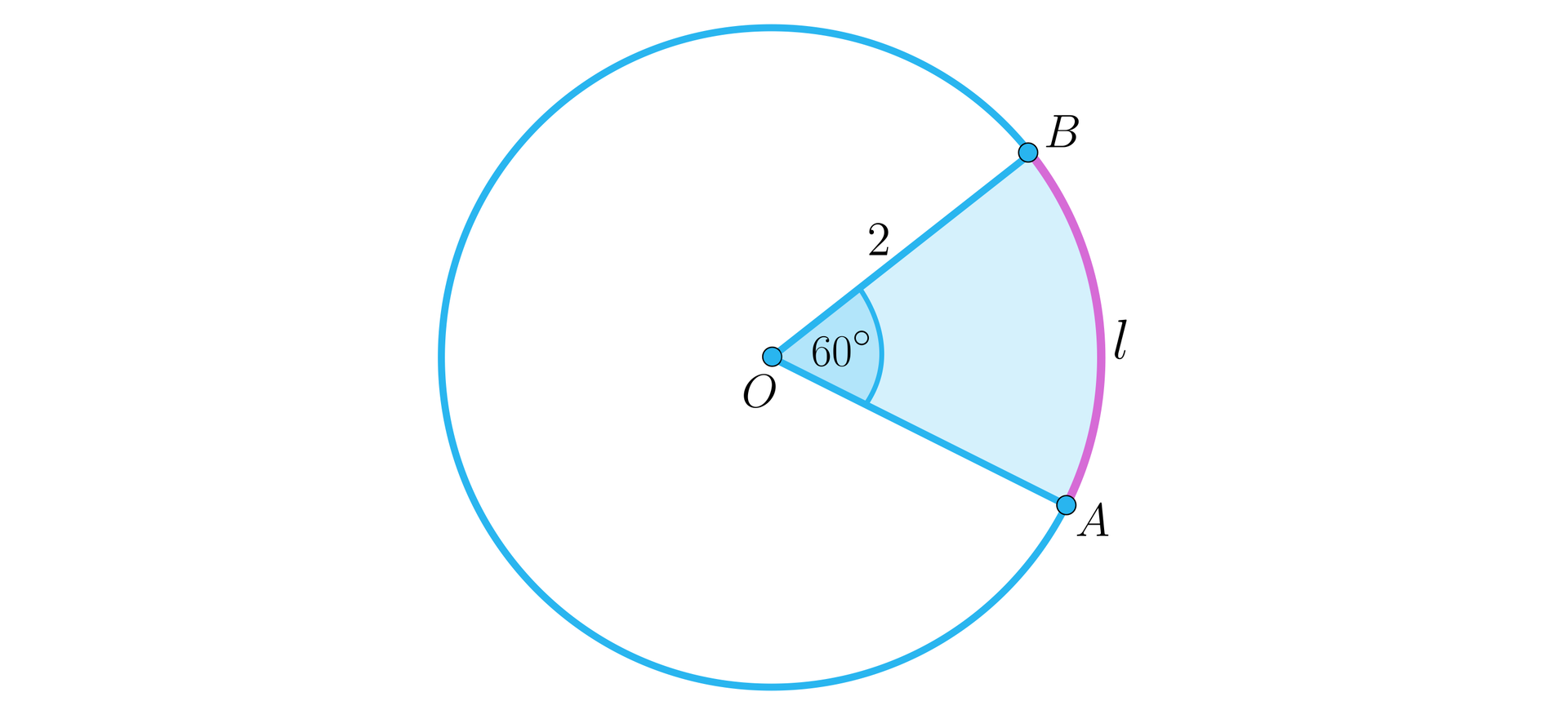
Wyznaczymy długość łuku $A B$ zaznaczonego na rysunku:

ReNEA9COrMc21

Ilustracja przedstawia okrąg. Punkt O jest środkiem okręgu. Na okręgu zaznaczono punktu A oraz B. Do końców tych punktów poprowadzono promienie. Promień okręgu wynosi dwa. Kąt środkowy powstałego wycinka wynosi 60 stopni, a długość łuku okręgu wyznaczanego przez ten kąt wynosi l.

Rozwiązanie

Promień okręgu ma długość $r = 2$ , zaś zaznaczony na rysunku kąt środkowy $∢ A O B = 60 °$ .

Korzystając ze wzoru na długość łuku okręgu mamy:

$l = 2 π r \cdot \frac{α}{360 °}$ ,

$l = 2 π \cdot 2 \cdot \frac{60 °}{360 °}$ ,

$l = 4 π \cdot \frac{1}{6}$ .

Ostatecznie otrzymujemy,

$l = \frac{4}{6} \cdot π = \frac{2}{3} π$ ,

zatem długość łuku $A B$ wynosi $\frac{2}{3} π$ .

W przypadku gdy znamy długość łuku okręgu oraz miarę kąta środkowegokąt środkowykąta środkowego opartego na owym łuku, możemy wyznaczyć długość promienia. Dość nieoczywiste zastosowanie tej obserwacji jest zaprezentowane w poniższym zadaniu:

Przykład 2

Koło samochodu w trakcie podróży na dystansie $100 \cdot π m$ wykonuje $200$ pełnych obrotów. Ile obrotów wykonałoby koło, którego promień jest o $20 %$ mniejszy na dystansie $400 \cdot π m$ ?

Rozwiązanie

Zacznijmy od wyznaczenia promienia koła wyjściowego samochodu. Zauważmy, że $200$ pełnych obrotów przekłada się na kąt $α = 200 \cdot 360 °$ , zatem $α = 72000 °$ . Podstawiając tę wartość pod wzór na długość łuku okręgu mamy:

$100 π m = 2 π r \cdot \frac{72000 °}{360 °}$ ,

$50 m = r \cdot 200$ ,

zatem $r = 0, 25 m$ . Zmniejszenie tej wielkości o $20 %$ oznacza, że mniejsze z rozważanych kół w zadaniu ma promień

$r_{2} = (100 - 20) % \cdot 0, 25 m = 0, 8 \cdot 0, 25 m = 0, 2 m$ .

Dysponując tą wiedzą ponownie wykorzystamy wzór na długość łuku okręgułuk okręgułuku okręgu – tym razem w celu wyznaczenia kąta $α_{2}$ , który pozwoli nam obliczyć liczbę wykonanych przez koło obrotów.

$400 π m = 2 π \cdot 0, 2 m \cdot \frac{α_{2}}{360 °}$

$1000 = \frac{α_{2}}{360 °}$ .

Z powyższego łatwo wnioskujemy, że mniejsze koło do przebycia dystansu $400 π m$ potrzebuje aż $1000$ obrotów.

Teraz przyjrzymy się nieco bardziej złożonej sytuacji, w której przydatna okazuje się wiedza z zakresu trygonometrii.

Przykład 3

W okręgu o średnicy $28 cm$ poprowadzono cięciwę, której odległość od środka okręgu wynosi $7 \sqrt{3} cm$ . Znajdziemy długość krótszego łuku opartego na cięciwie.

Rozwiązanie

Długość średnicy wynosi $28 cm$ , zatem długość promienia wynosi $14 cm$ . Odcinek łączący wspomnianą w zadaniu cięciwę ze środkiem okręgu pada na nią pod kątem prostym. Oznacza to, że cięciwa wraz z promieniami tworzy trójkąt równoramienny o wysokości $h = 7 \sqrt{3} cm$ . Zatem kąt przy podstawie tak utworzonego trójkąta ma miarę:

$\sin α = \frac{7 \sqrt{3}}{14}$

$\sin α = \frac{\sqrt{3}}{2}$

$α = 60 °$ .

Sytuację obrazuje poniższy rysunek:

R1MZydftGOMoE

Ilustracja przedstawia okrąg. Punkt O to środek okręgu. Zaznaczono średnicę okręgu, wynosi ona dwadzieścia osiem. Zaznaczono również na okręgu punkty A oraz B. Poprowadzono odcinek od punktu A do B, jest on równoległy do poprowadzonej średnicy. Na okręgu powstała cięciwa A B. W połowie cięciwy A B zaznaczono punkt C. Z punktu O poprowadzono odcinki do punktów A B oraz C. Tak powstał trójkąt O A B, o wysokości O C. Oba odcinki O A oraz O B to promienie okręgu, oba wynoszą czternaście, natomiast długość odcinka O C wynosi 73. Zaznaczono kąty O A B oraz A B O, są one sobie równe i wynoszą 60 stopni.

Zatem trójkąt ten jest równoboczny, czyli miara kąta środkowego wynosi $60 °$ . Długość krótszego łuku opartego na tej cięciwie wynosi zatem

$l = 2 π \cdot 14 \cdot \frac{60 °}{360 °} = 4 \frac{2}{3} π$ .

W ostatnim przykładzie przyjrzyjmy się dość niestandardowej figurze geometrycznej, z którą jednak miewamy styczność w naszej codziennej rzeczywistości:

Przykład 4

Śmigło wiatraka przemysłowego składa się z ośmiu identycznych łopatek o łącznej powierzchni $8 π {cm}^{2}$ . Wiedząc, że średnica wiatraka wynosi $4 \sqrt{3} cm$ obliczymy łączny obwód łopatek tego śmigła.

Rozwiązanie

Zacznijmy od szkicu opisywanej w zadaniu figury:

Rvx7X7Scffl48

Ilustracja przedstawia okrąg. Środek okręgu oznaczono jako S. Na okręgu zaznaczono średnicę, pomiędzy punktami C oraz D. Poprowadzono więcej średnic, w taki sposób, że na okręgu powstało 8 równych wycinków koła. Długość łuku okręgu pomiędzy sąsiednimi wycinkami wynosi tyle samo dla każdego wycinka.

Widzimy zatem, że obwód figury będzie sumą szesnastu długości promienia i łącznej długości wszystkich łuków wycinków tworzących skrzydła wiatraka. Pozostaje nam tylko wyznaczyć te dwie wielkości.

Pierwsza z nich jest niemal bezpośrednio podana w warunkach zadania – długość średnicy wiatraka wynosi $4 \sqrt{3} cm$ , co przekłada się na fakt, iż promień koła, którego wycinki składają się na wiatrak, wynosi $2 \sqrt{3} cm$ .

Każda łopatka ma pole powierzchni równe

$P_{l} = \frac{1}{8} \cdot 8 π {cm}^{2} = π {cm}^{2}$ .

Podstawiając do wzoru na pole powierzchni wycinka kąta znane nam informacje, uzyskujemy równanie umożliwiające wyznaczenie kąta środkowego $α$ . Mamy zatem:

$π = π {(2 \sqrt{3})}^{2} \cdot \frac{α}{360 °}$

$1 = \frac{12 α}{360 °}$

$α = 30 °$ .

Znając wartość kąta środkowego odpowiadającego pojedynczemu skrzydłu wiatraka, jesteśmy w stanie wyliczyć długość łuku, na którym się opiera.

$l = 2 π 2 \sqrt{3} \cdot \frac{30 °}{360 °} = \frac{\sqrt{3}}{3} π cm$

Powołując się na obserwacje z pierwszego etapu naszej pracy, obliczamy końcowy wynik (tj. łączny obwód łopatek wiatraka):

$L = 16 \cdot r + 8 \cdot l = 16 \cdot 2 \sqrt{3} cm + \frac{8 \sqrt{3}}{3} π cm = (32 \sqrt{3} + \frac{8 \sqrt{3}}{3} π) cm$ .

Słownik

łuk okręgu

część okręgu wyznaczona przez ramiona kąta środkowego tego okręgu

kąt środkowy

kąt, którego wierzchołkiem jest środek tego okręgu, a ramionami są półproste zawierajace promienie tego okręgu

kąt pełny

kąt o mierze równej $360 °$

Wprowadzenie

Aplet

Słownik