Przeczytaj
Rozpoczniemy od przypomnienia definicji wykresu funkcji.
Wykres funkcji jest to zbiór wszystkich punktów płaszczyzny o współrzędnych , w prostokątnym układzie współrzędnych, gdzie należy do dziedziny tej funkcji, natomiast jest wartością funkcji dla argumentu .
Poniższe przykłady pokażą sposób określania dziedziny funkcji opisanej za pomocą wykresu.
Na lekcjach chemii posługujemy się pojęciem rozpuszczalności.
Rozpuszczalność substancji to maksymalna ilość tej substancji, wyrażona w gramach, którą można rozpuścić w gramach rozpuszczalnika w danej temperaturze.
Poniżej przedstawione są wykresy rozpuszczalności kilku substancji. Określ dziedzinę funkcji, która temperaturze (w stopniach Celsjusza) przyporządkowuje rozpuszczalność danej substancji (w g na g wody).

Rozwiązanie:
Dziedzinę funkcji odczytujemy na osi poziomej. Do dziedziny funkcji należą liczby określające temperaturę.
Funkcja opisana jest za pomocą wykresu. Określimy jej dziedzinę.
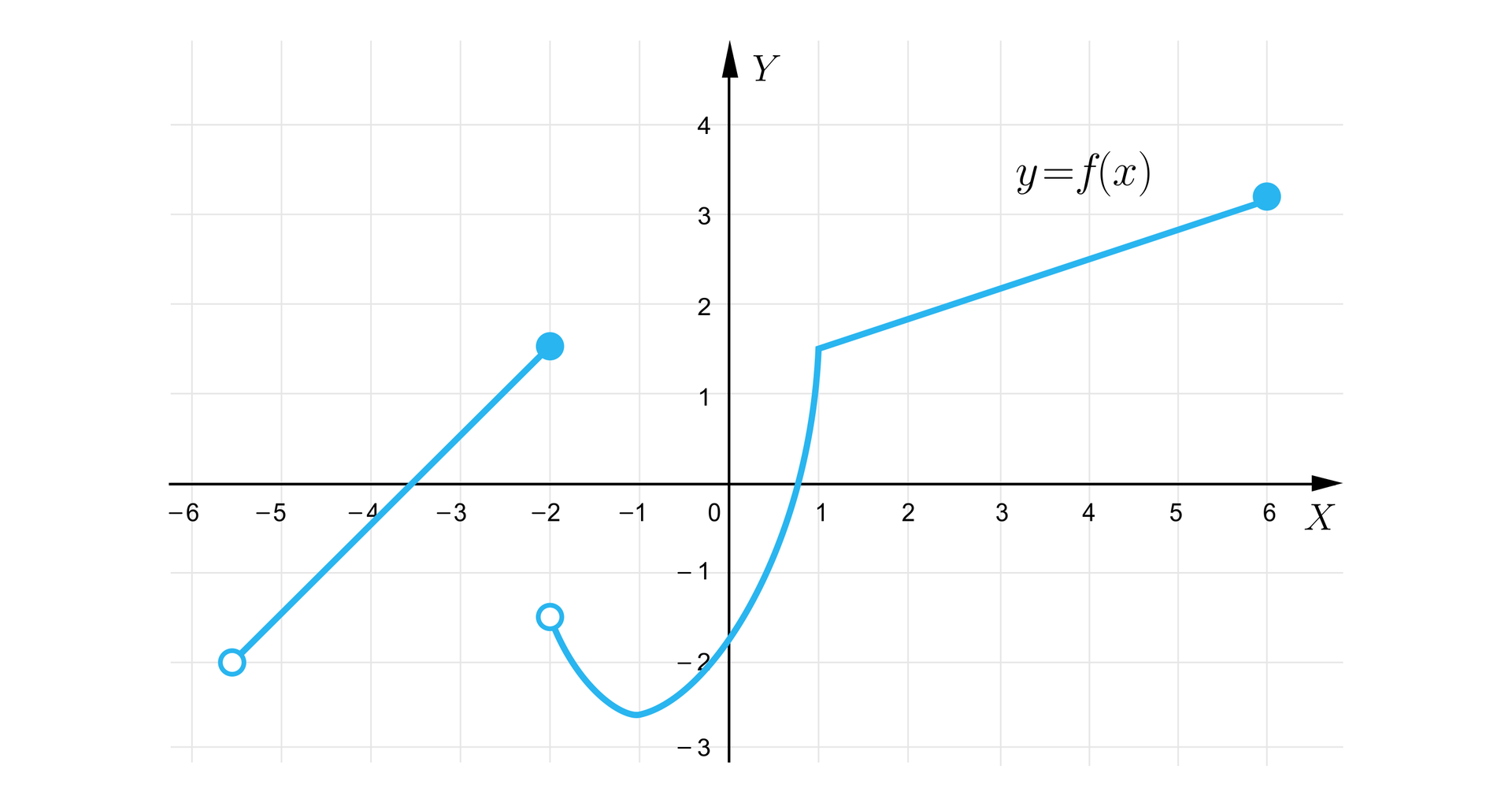
Rozwiązanie:
Wiemy, że wykres funkcjiwykres funkcji w prostokątnym układzie współrzędnych to zbiór wszystkich punktów płaszczyzny o współrzędnych , gdzie oznacza argument funkcji, jest wartością funkcji dla argumentu .
Aby z wykresu odczytać dziedzinę funkcji należy odcięte wszystkich punktów należących do dziedziny zrzutować prostopadle na oś .
Na osi powstaje zbiór wszystkich argumentów funkcji, czyli dziedzina funkcji.

W przypadku naszego wykresu dziedziną funkcji jest zbiór:
W prostokątnym układzie współrzędnych przedstawiony jest wykres funkcjiwykres funkcji . Korzystając z wykresu funkcji określimy jej dziedzinę.

Rozwiązanie:

Dziedzina funkcji to:
Korzystając z wykresu funkcji , przedstawionym w prostokątnym układzie współrzędnych, określimy dziedzinę tej funkcji.
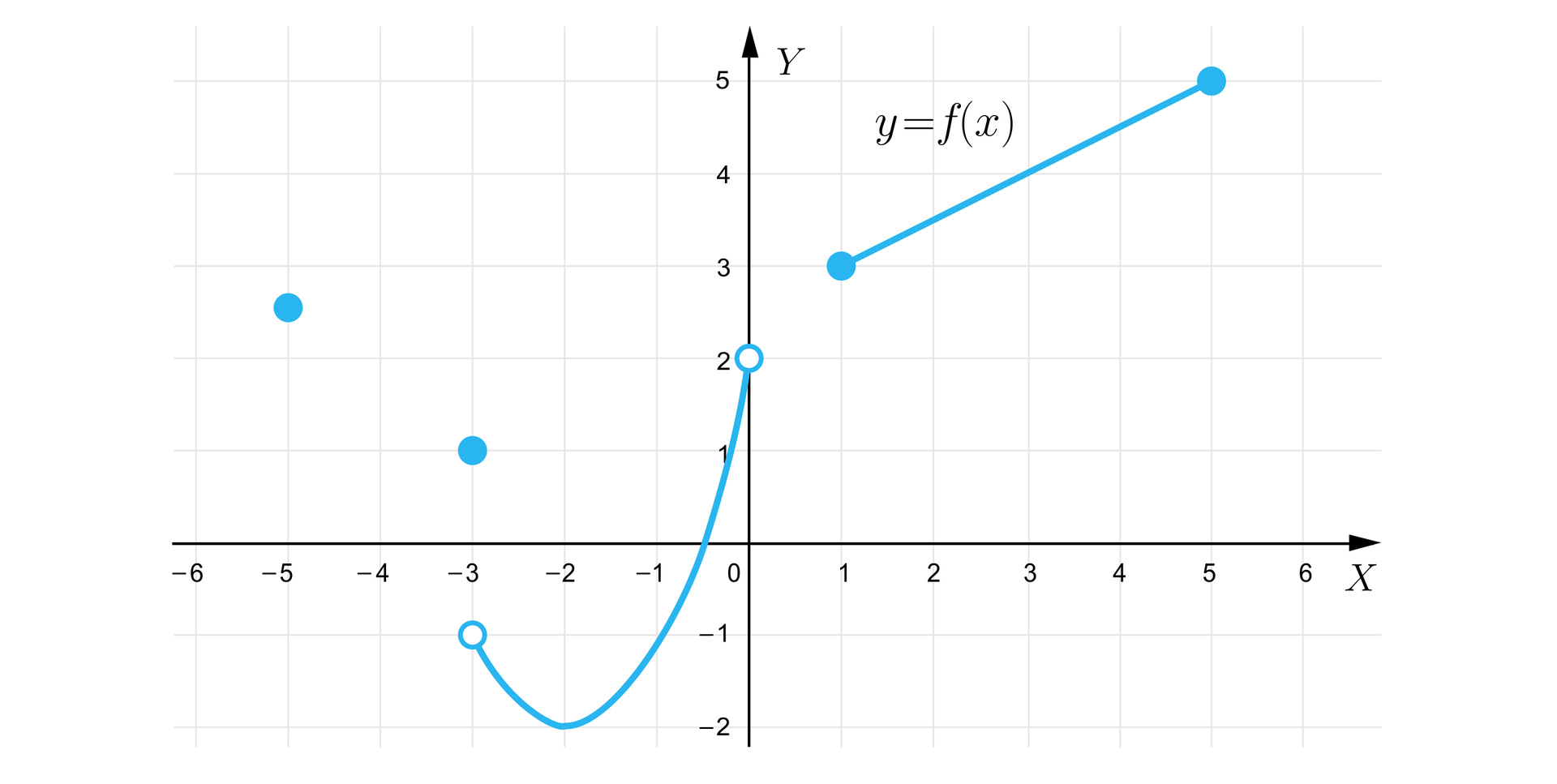
Rozwiązanie:
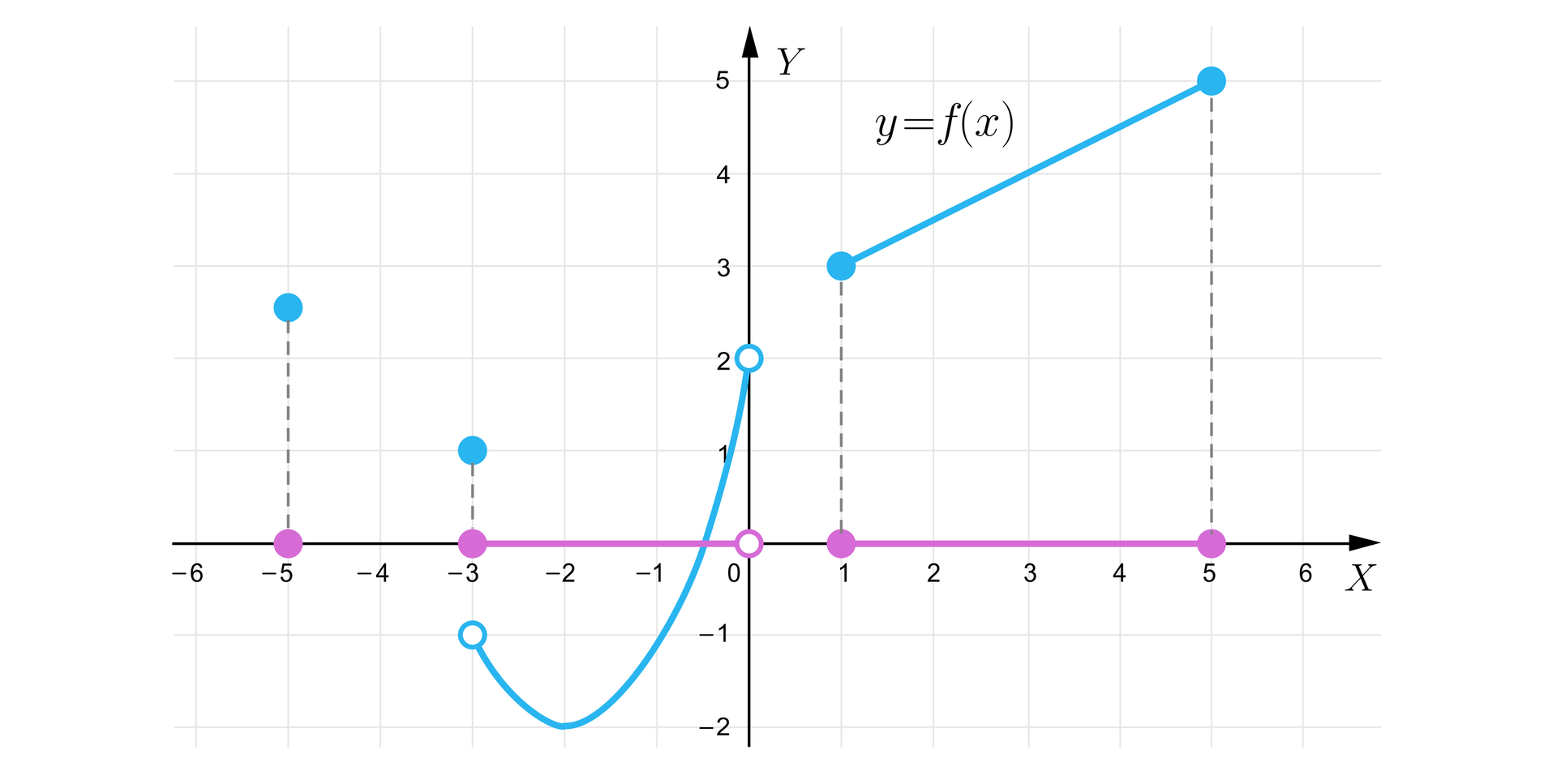
Dziedzina funkcji to:
Określimy dziedzinę funkcji przedstawionej za pomocą wykresu.
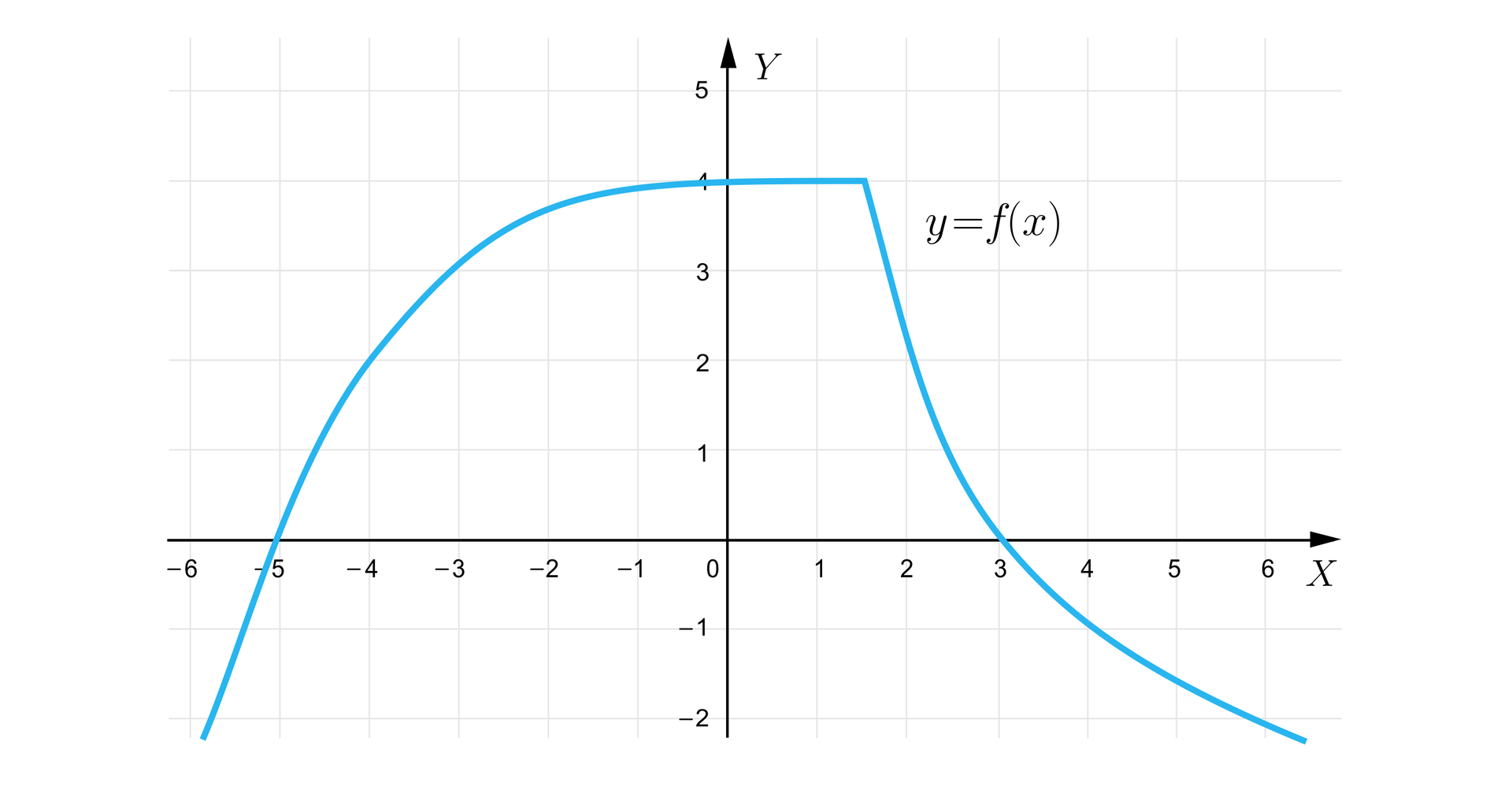
Rozwiązanie:
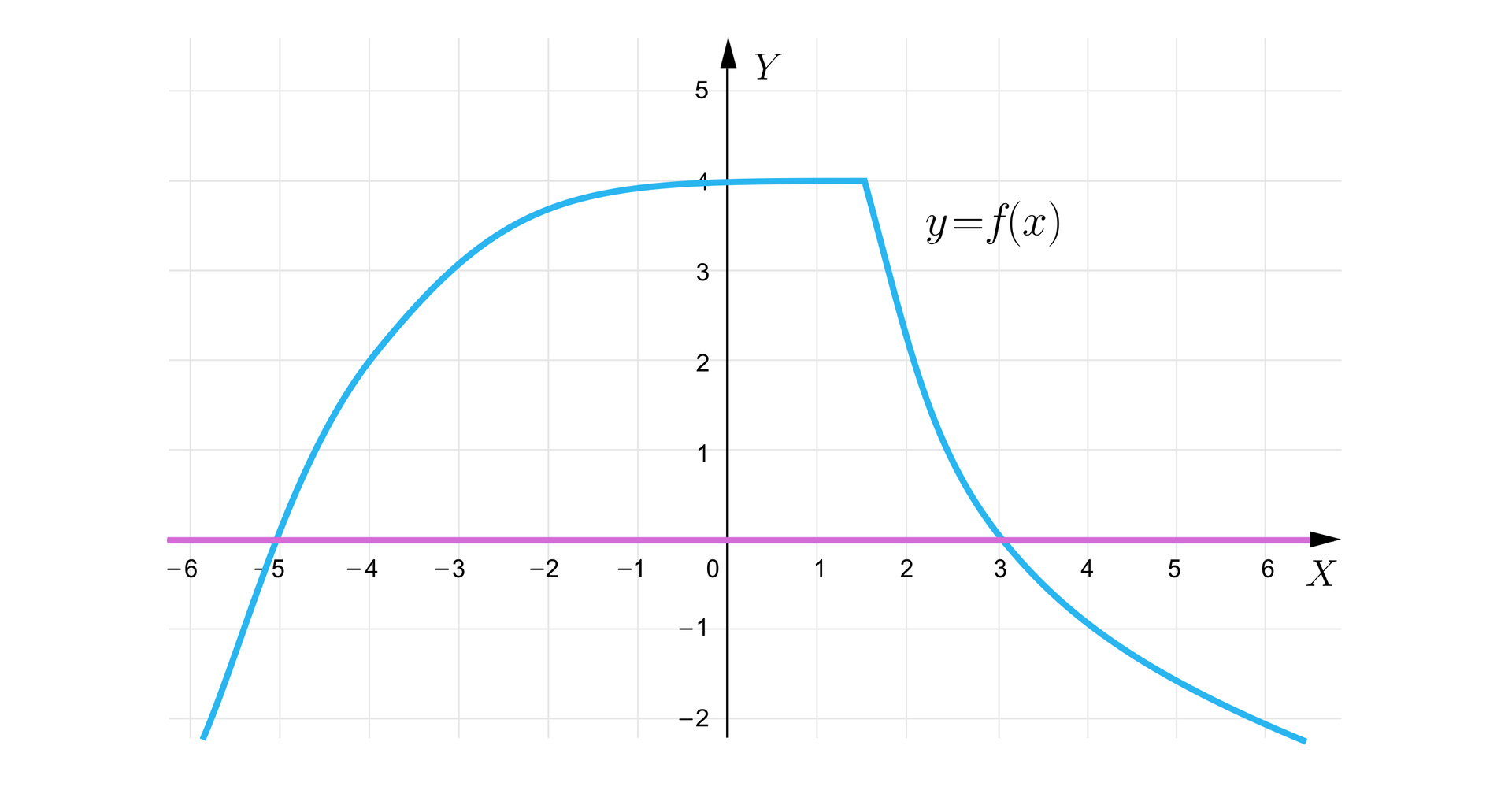
Do dziedziny funkcji należą wszystkie liczby rzeczywiste:
Słownik
wykres funkcji jest to zbiór wszystkich punktów płaszczyzny o współrzędnych , w prostokątnym układzie współrzędnych, gdzie należy do dziedziny tej funkcji, natomiast jest wartością funkcji dla argumentu