Przeczytaj
Kąty pomiędzy odcinkami w sześcianie
W pierwszej części materiału omówimy kąty pomiędzy krawędziami sześcianu i jego przekątnymi oraz kąty pomiędzy przekątnymi w sześcianie.
Kąt między krawędzią a przekątną ściany
Jeżeli krawędź i przekątna ściany leżą na tej samej ścianie, to kąt pomiędzy nimi wynosi . Wynika to z faktu, że trójkąt prostokątny, którego bokami są krawędź i przekątna ściany jest równoramienny.
Kąt pomiędzy krawędzią a przekątną ściany, z którą ma wspólny wierzchołek, ale nie leży na tej samej ścianie sześcianu jest kątem prostym. Wynika to z faktu, że sąsiednie ściany boczne w sześcianie są prostopadłe. Dwa odcinki leżące na płaszczyznach prostopadłych są do siebie prostopadłe.
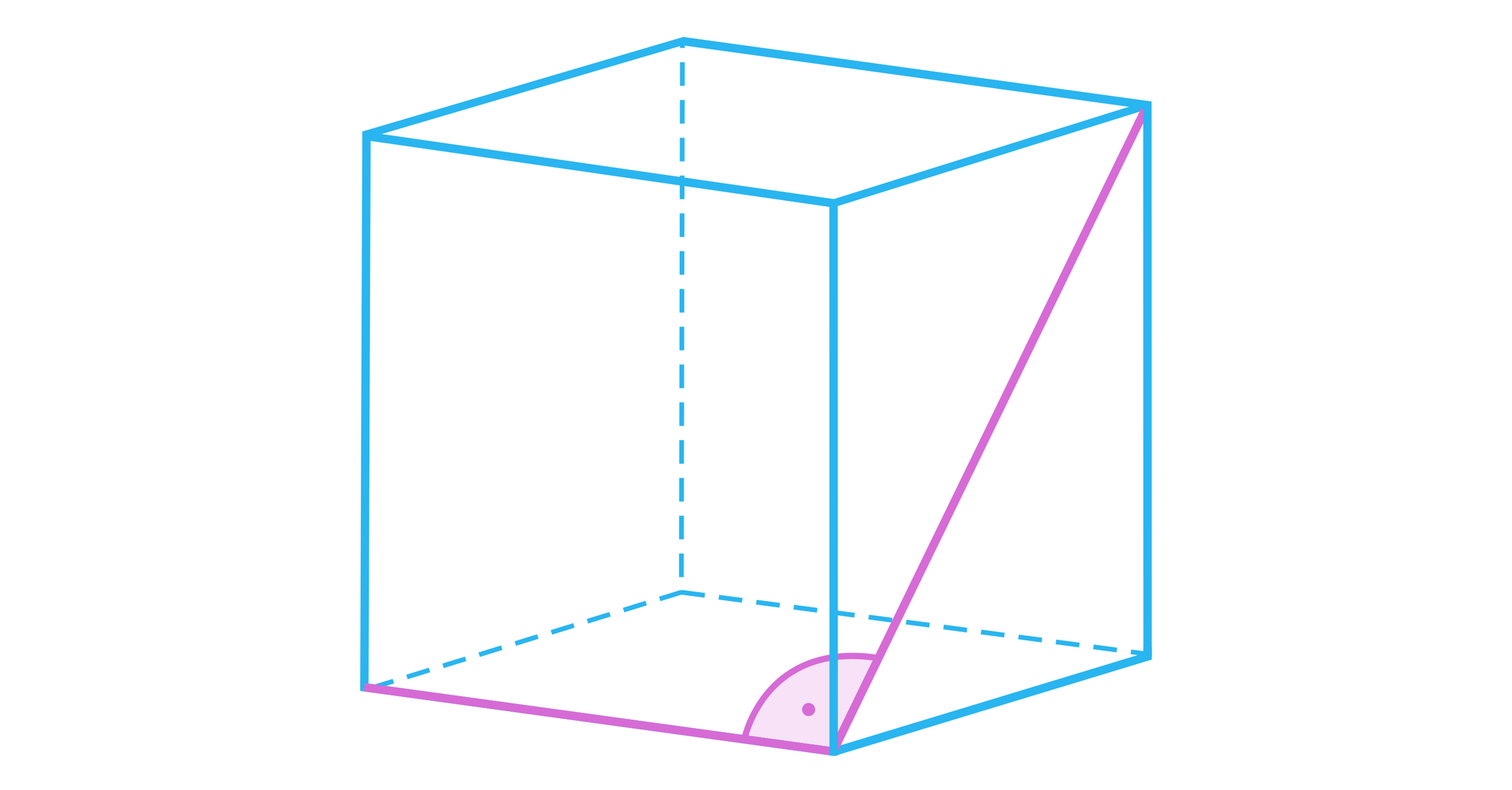
Kąt pomiędzy krawędzią a przekątną sześcianu
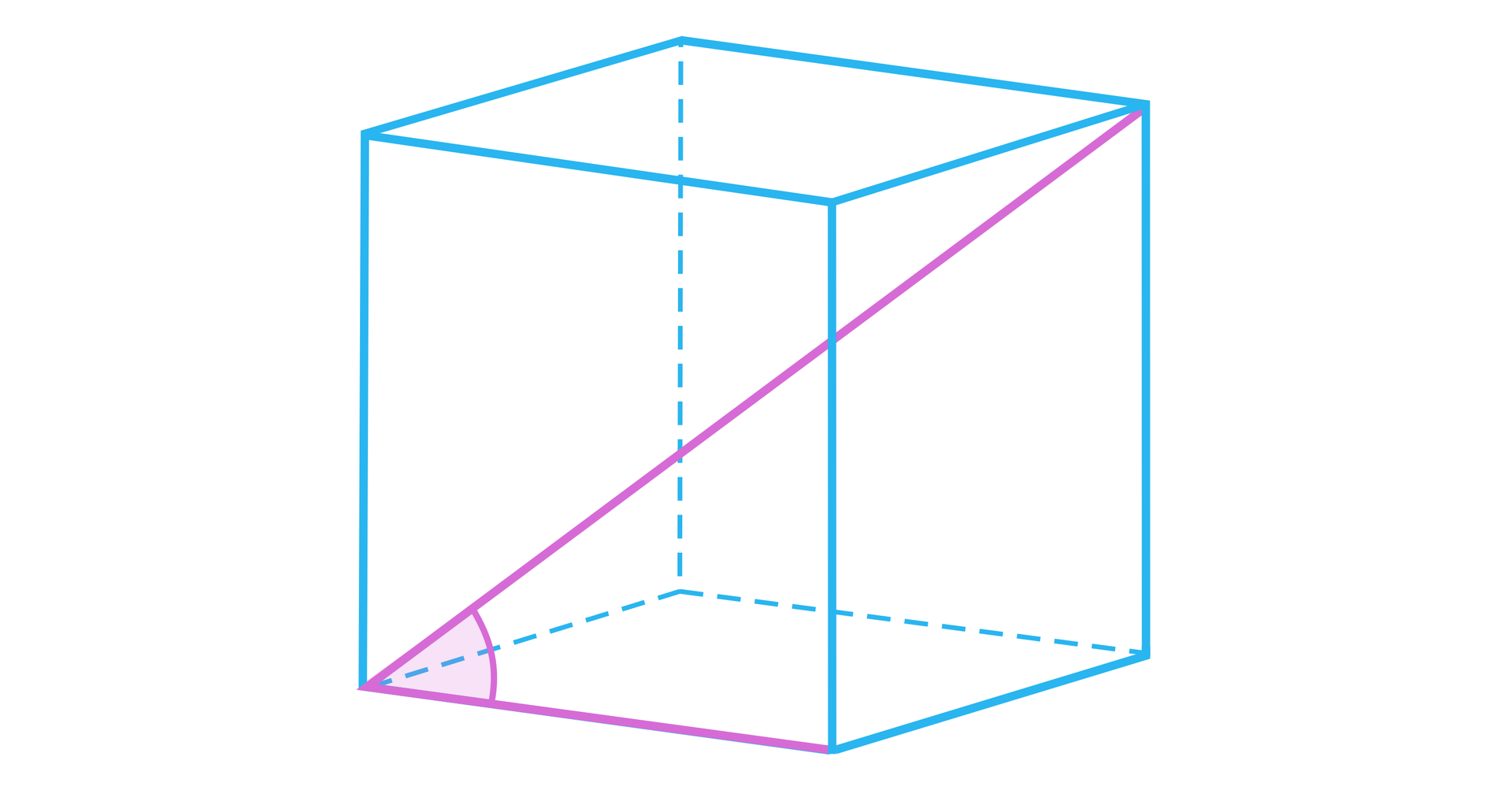
Kąt między przekątną ściany a przekątną sześcianu
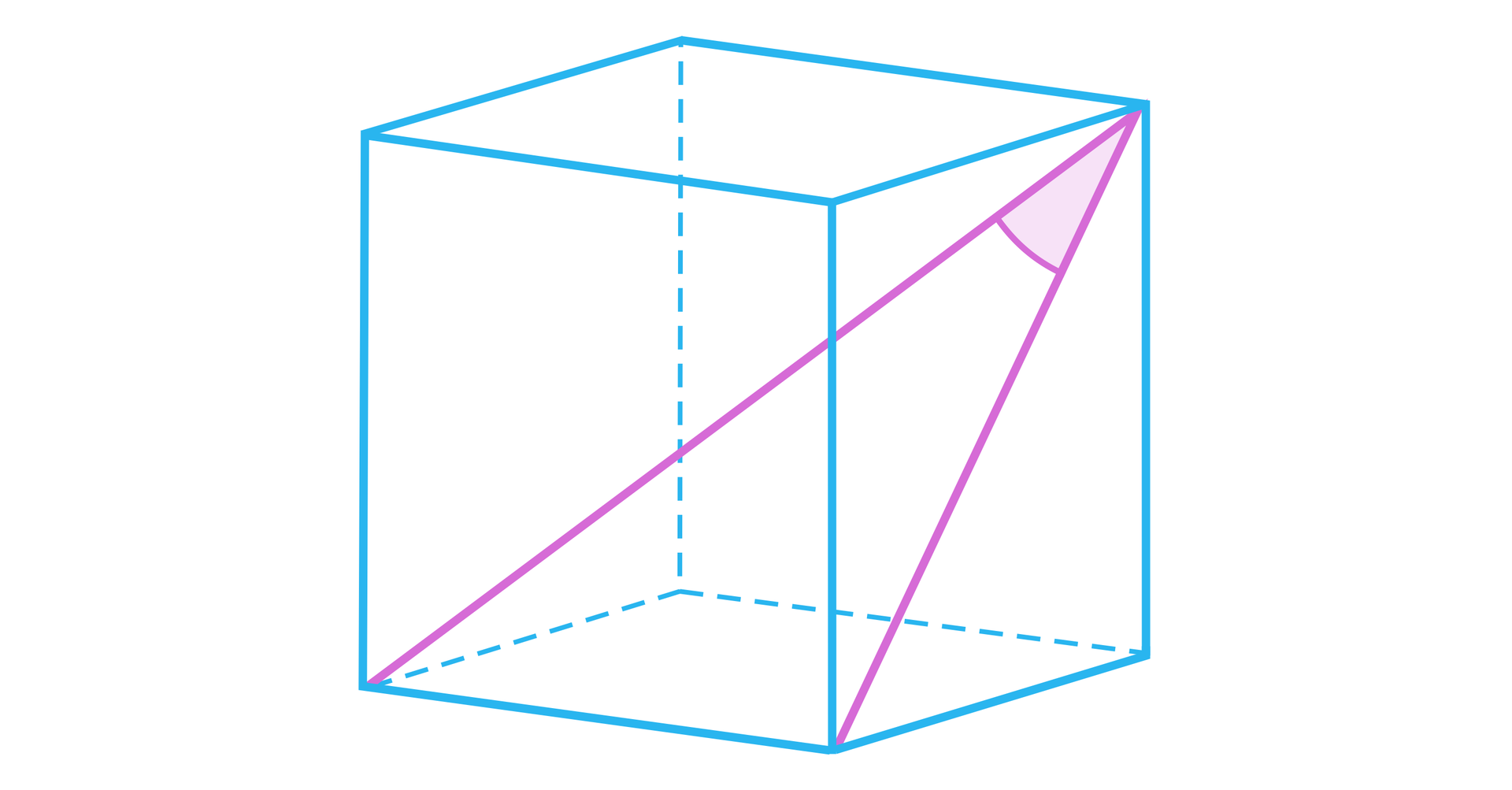
Trzy ostatnie przedstawione kąty są kątami tego samego trójkąta prostokątnego.
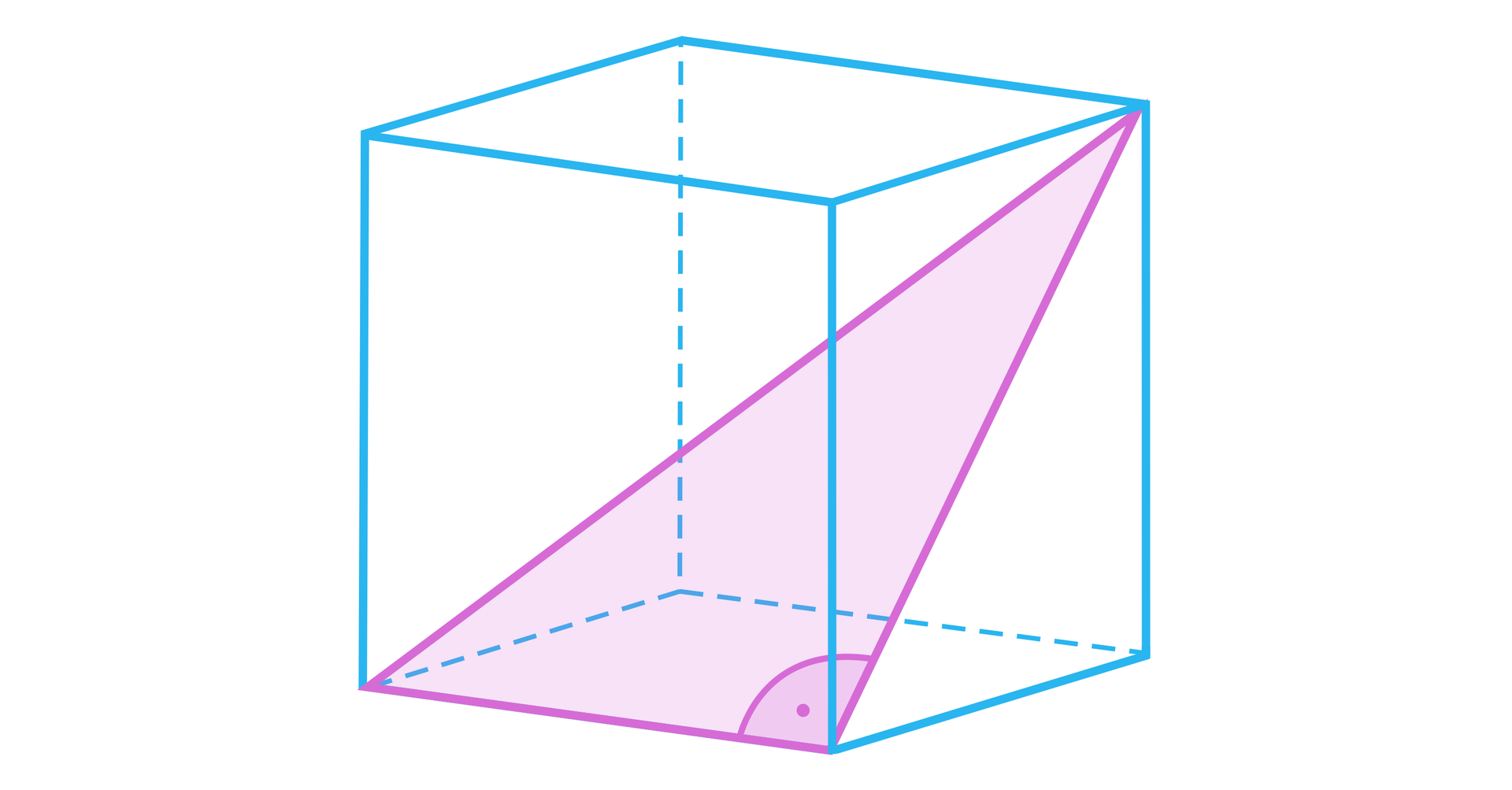
Obliczymy sinus kąta pomiędzy przekątną ściany bocznej a przekątną sześcianukąta pomiędzy przekątną ściany bocznej a przekątną sześcianu.
Rozwiązanie
Znamy już zależności pomiędzy odcinkami w sześcianie. Zróbmy rysunek pomocniczy.
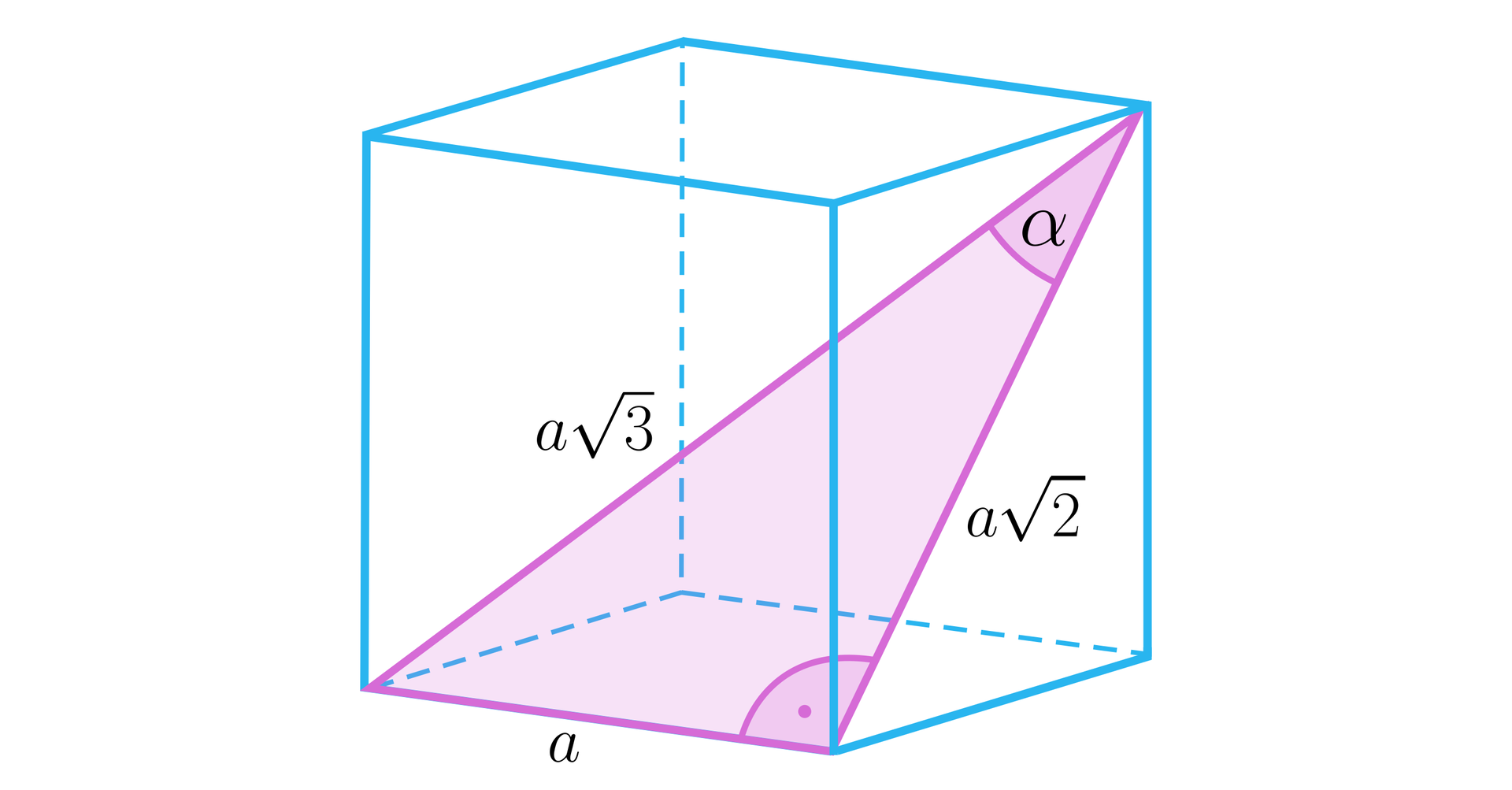
Skorzystajmy z funkcji trygonometrycznych w trójkącie zaznaczonym na rysunku. Mamy więc .
Kąt pomiędzy przekątną sześcianu i przekątną ściany bocznej wychodzących z tego samego wierzchołka ma tę stałą miarę dla każdego sześcianu. Ponieważ , to .
Kąt pomiędzy krawędzią podstawy, a przekątną sześcianu wychodzącymi z tego samego wierzchołka ma miarę około .
Kąt pomiędzy przekątnymi sąsiednich ścian bocznych wychodzącymi ze wspólnego wierzchołka
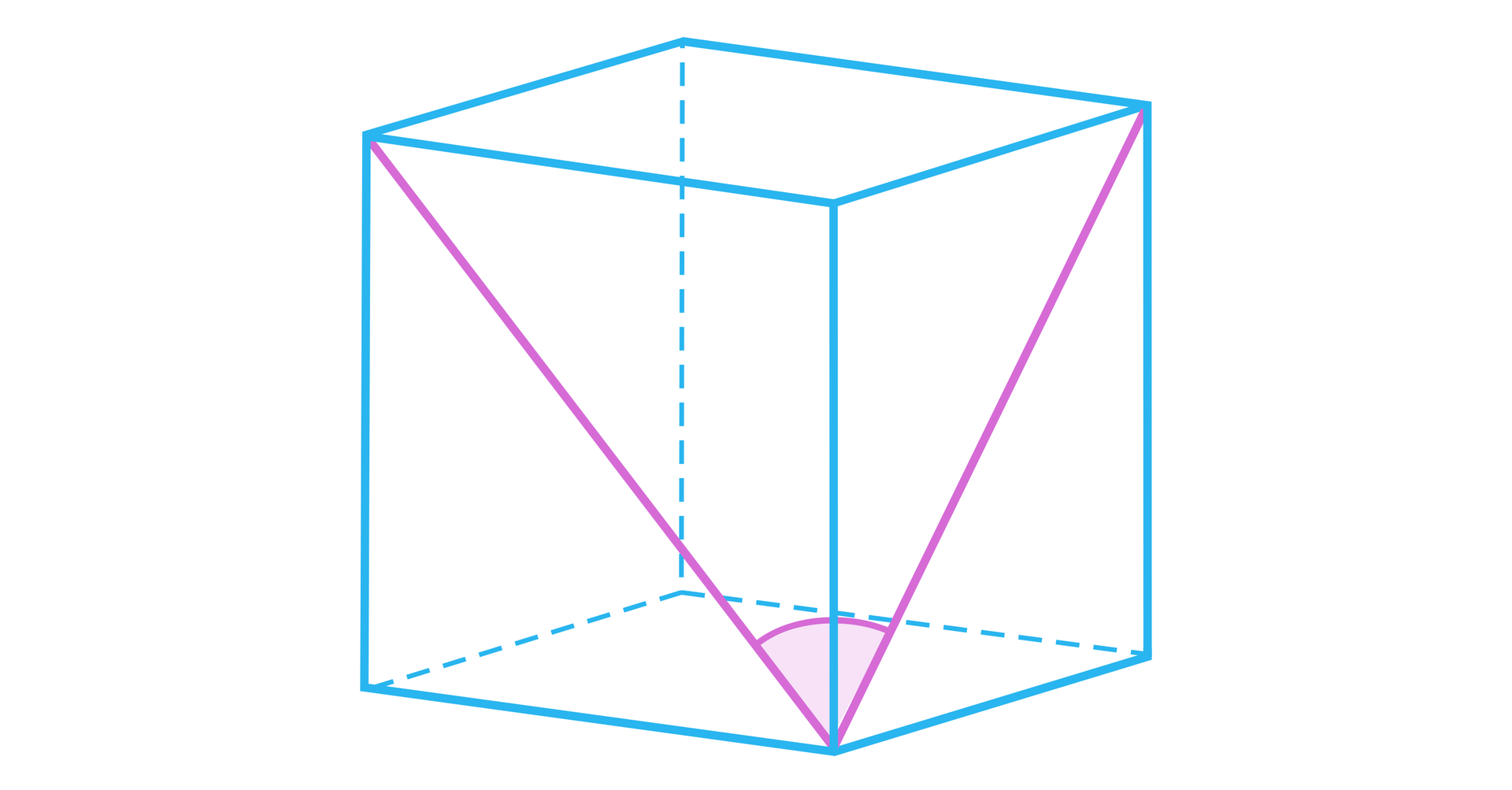
Kąt pomiędzy przekątnymi sąsiednich ścian bocznych wychodzącymi ze wspólnego wierzchołka jest kątem trójkąta, którego boki są przekątnymi ścian sześcianu. Trójkąt ten jest równoboczny, a zatem kąt między przekątnymi ścian ma miarę .
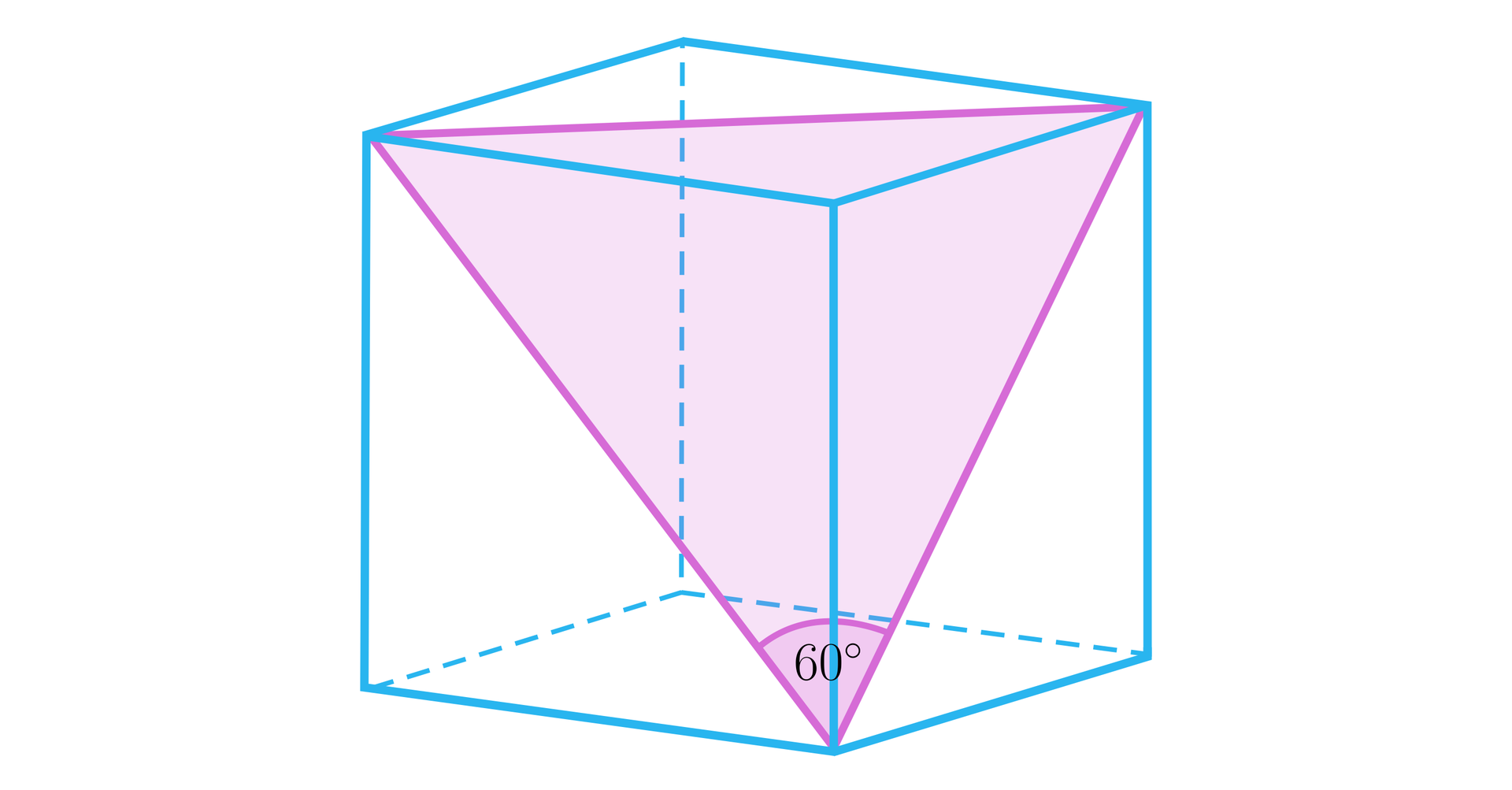
Kąty pomiędzy przekątnymi sześcianu
Przekątne sześcianu przecinają się w punkcie, który dzieli je na połowy.
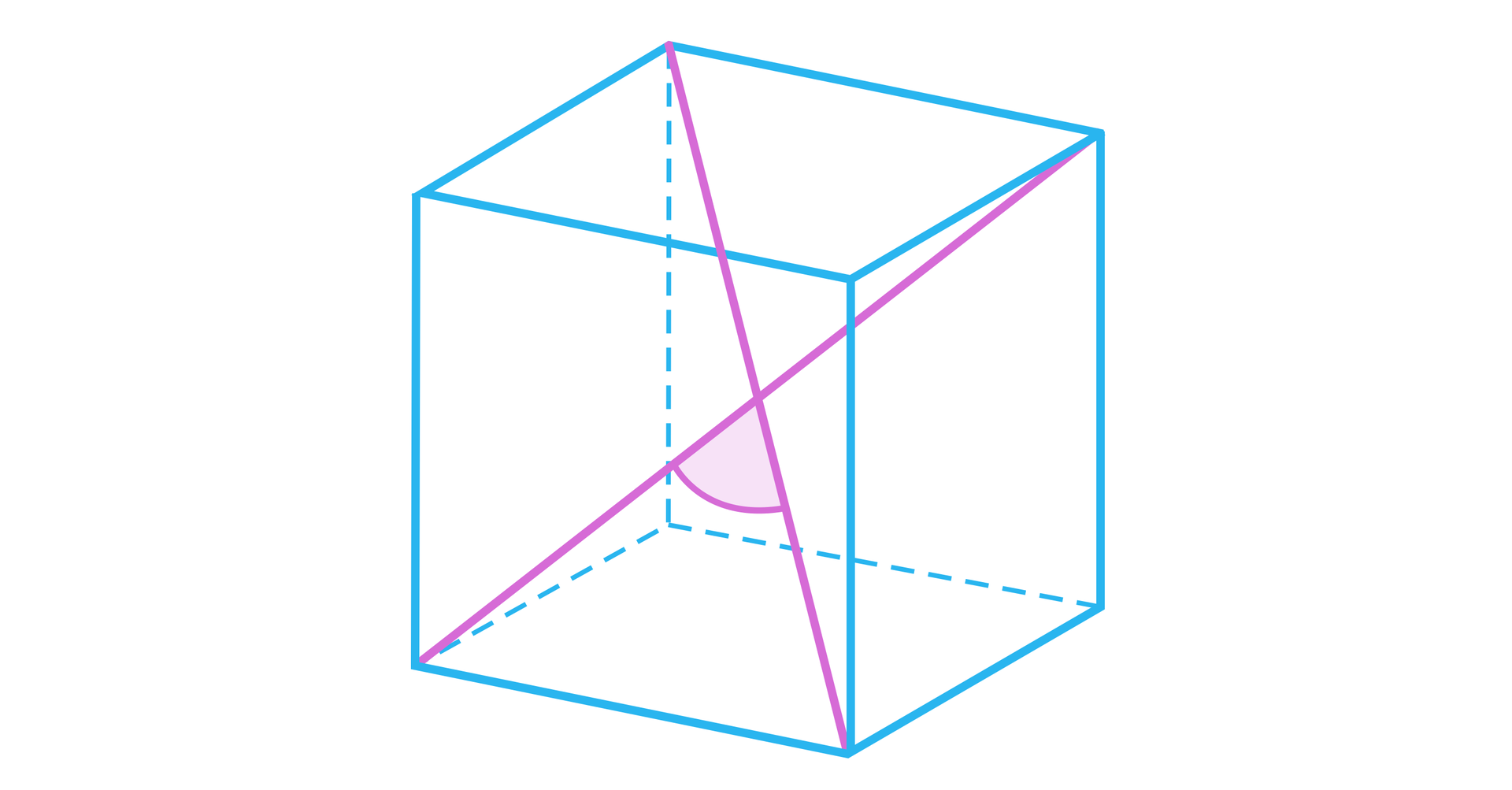
Uzasadnimy, że przekątne sześcianu przecinają się w punkcie, który dzieli je na połowy.
Rozwiązanie
Zróbmy rysunek pomocniczy:
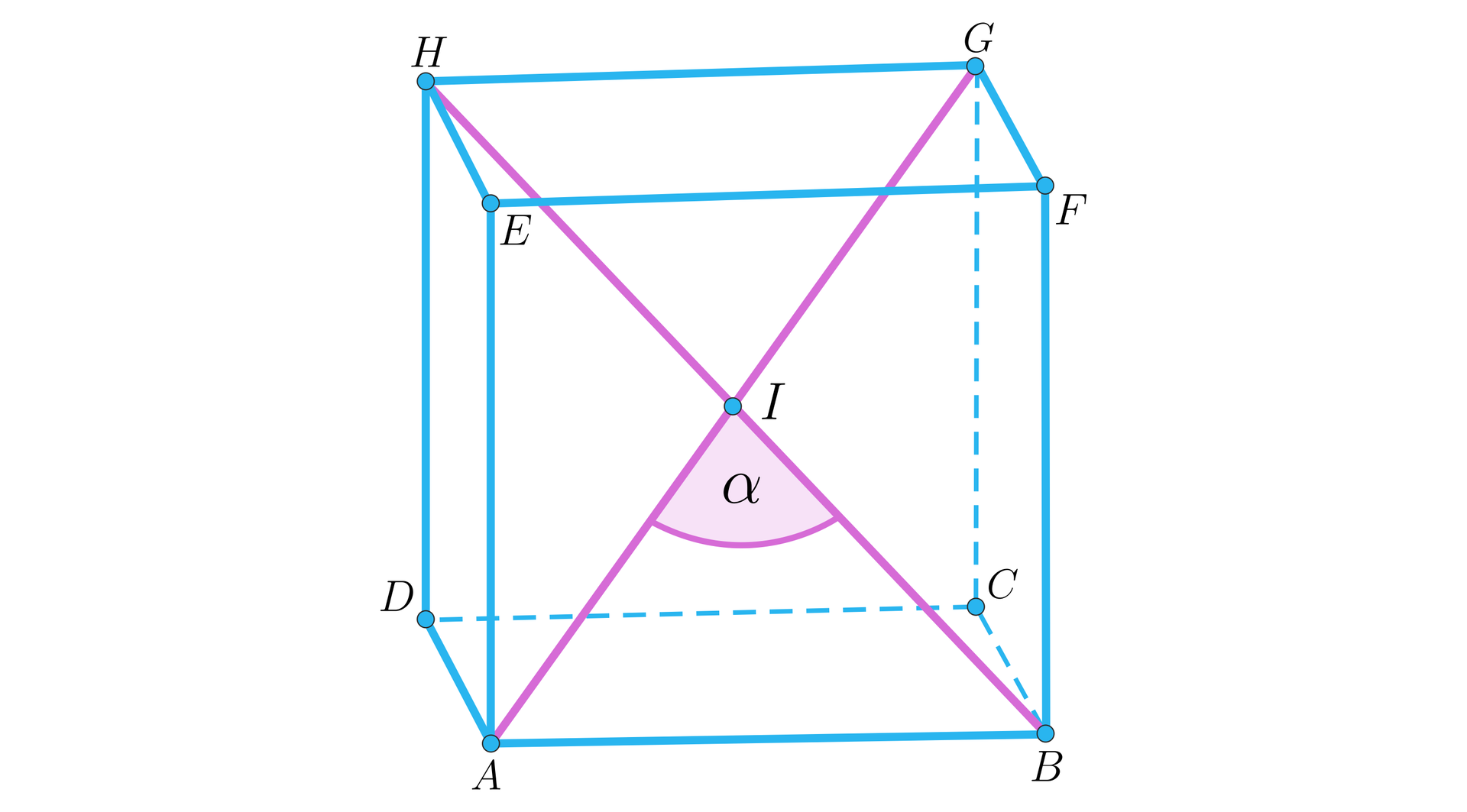
Kąty , , , to kąty pomiędzy przekątną sześcianu a krawędzią sześcianu wychodzących z tego samego wierzchołka, a zatem mają tę samą miarę. Ponadto . A zatem trójkąty równoramienne i są przystające (cecha ). A stąd . A zatem punkt dzieli przekątne sześcianu i na połowy.
Korzystając z sumy miar kątów w trójkącie otrzymujemy, że kąt pomiędzy przekątnymi sześcianu ma miarę około .
Inne kąty między odcinkami
W sześcianie możemy również wyróżnić inne kąty między jego odcinkami, których wartości jesteśmy w stanie obliczyć.
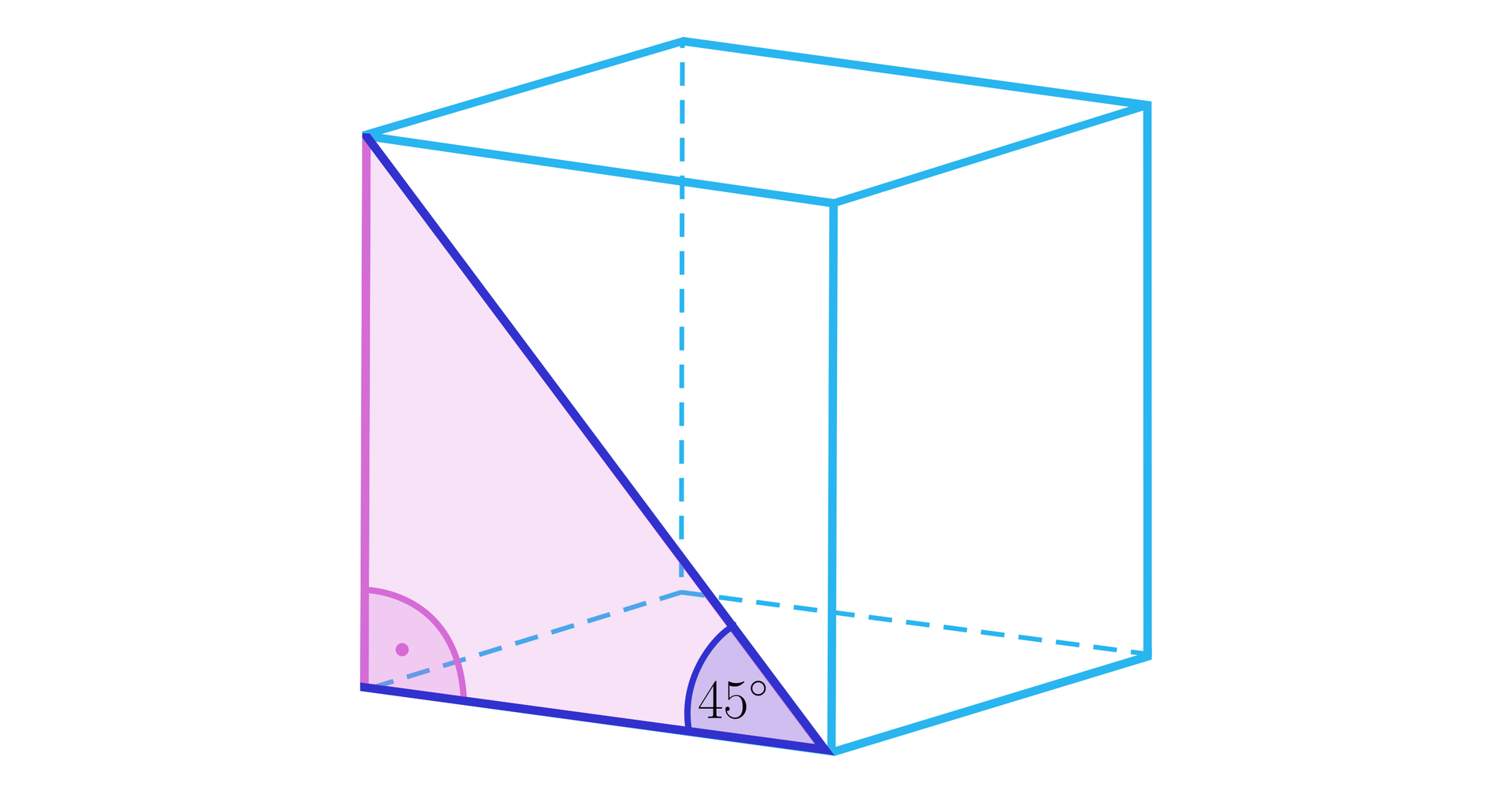
Dany jest sześcian jak na rysunku. Obliczymy miarę kąta .
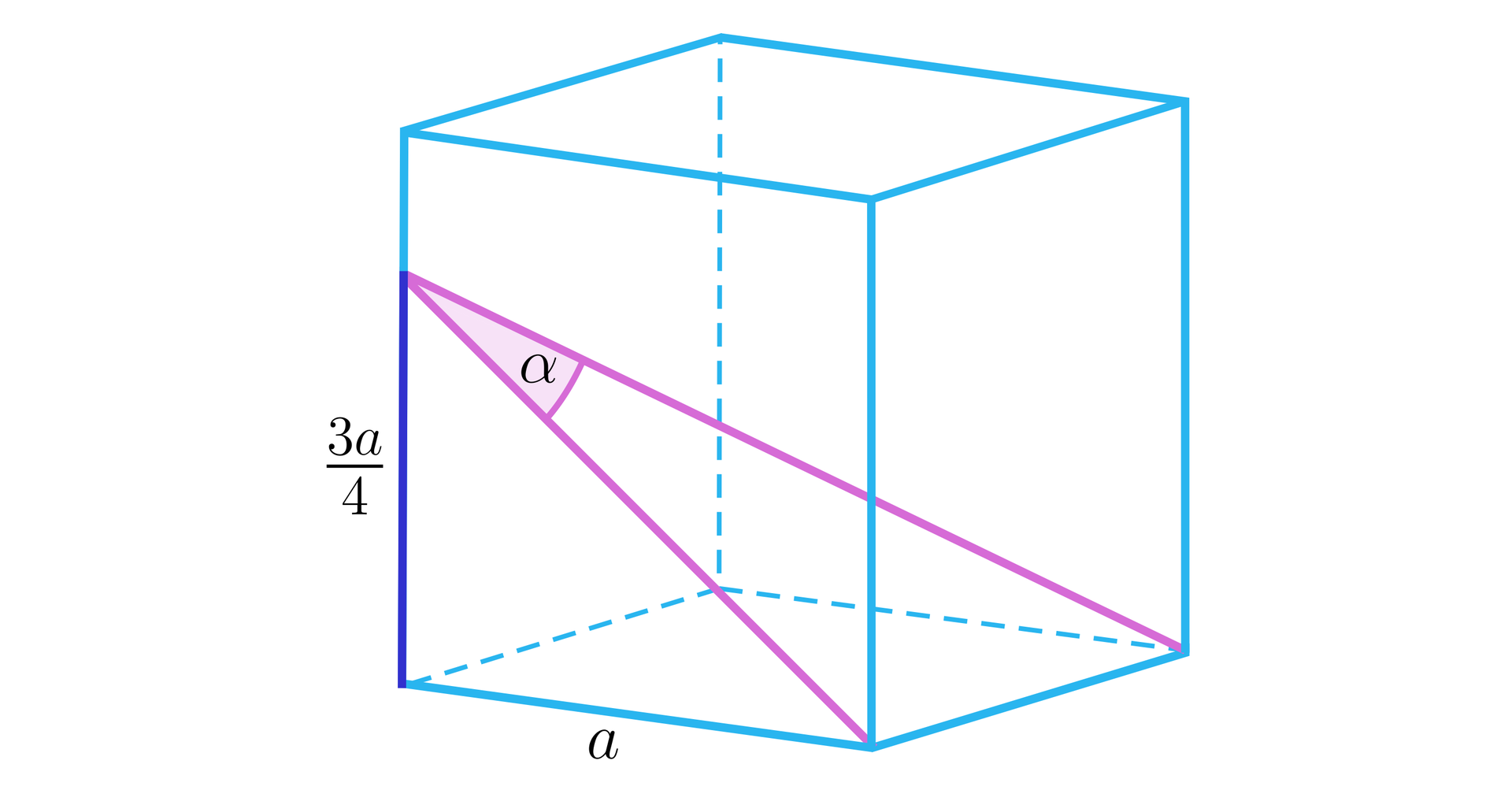
Rozwiązanie
Aby obliczyć długość jednego z odcinków zawartych w ramionach kąta, wykorzystamy trójkąt prostokątny.
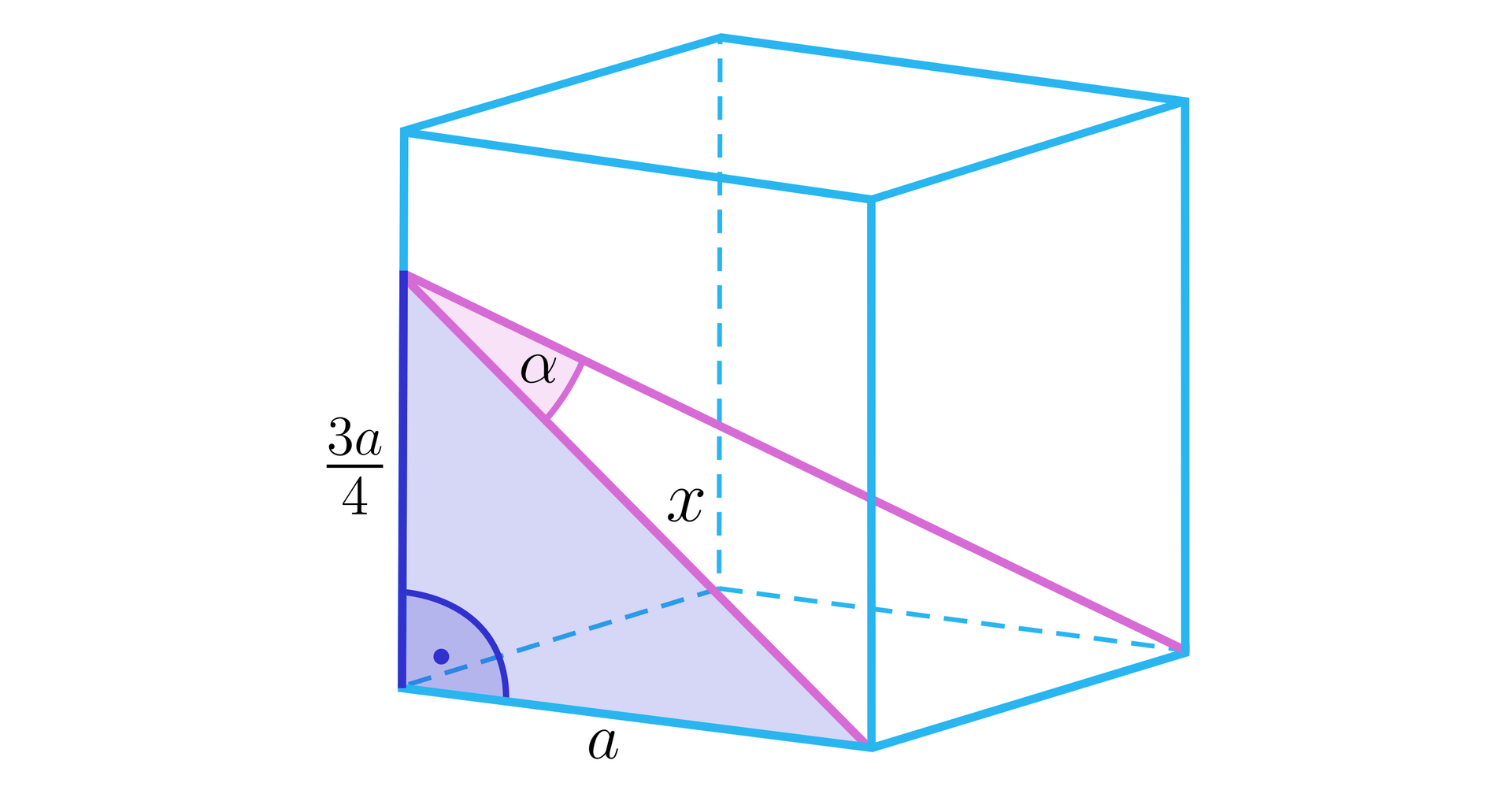
Obliczymy długość odcinka oznaczonego przez z Twierdzenia Pitagorasa:
.
A stąd i ostatecznie .
A teraz skorzystamy z funkcji trygonometrycznych kąta ostrego w trójkącie prostokątnym zaznaczonym na rysunku poniżej.
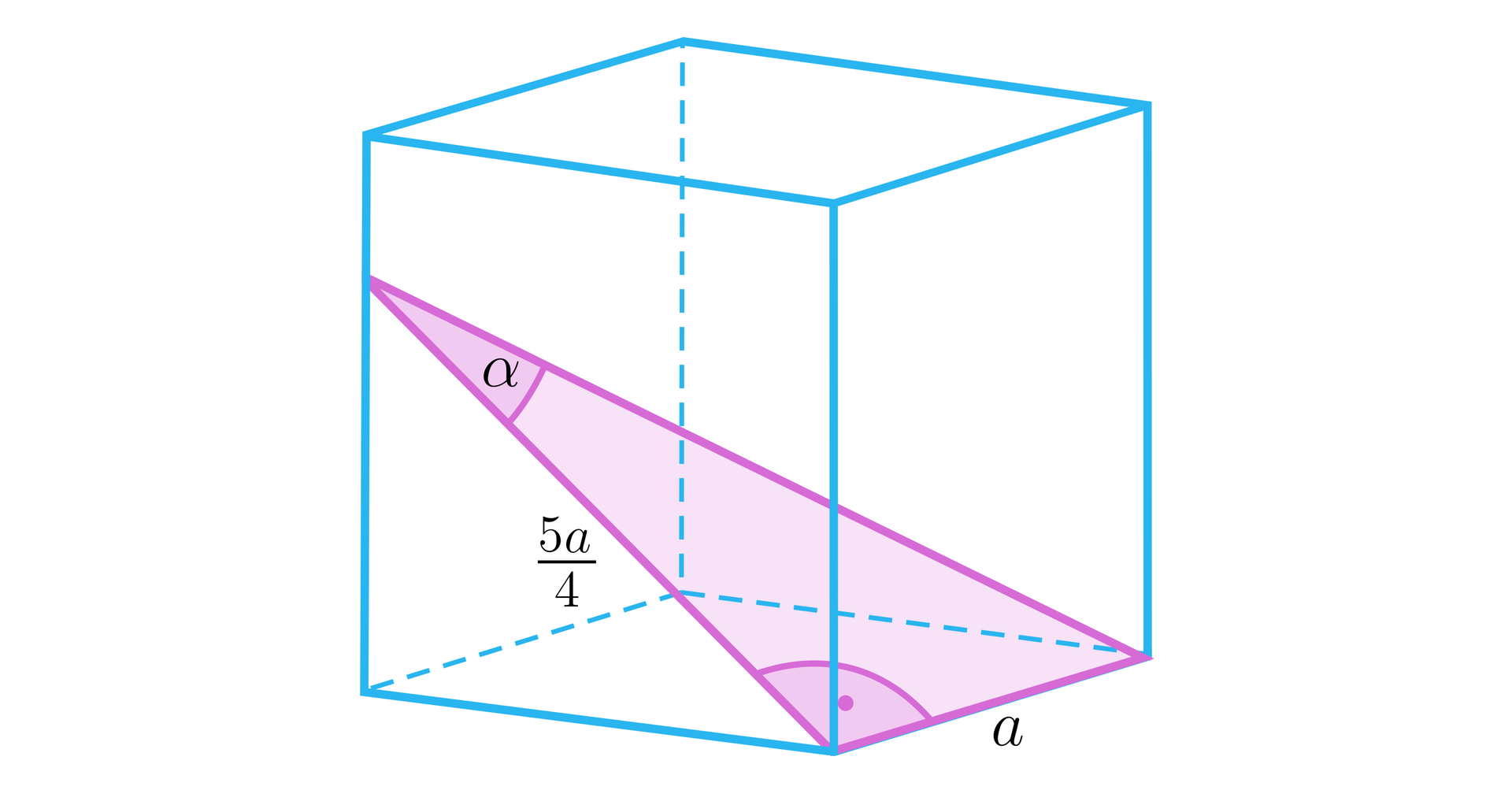
Mamy więc . A zatem .
Kąty pomiędzy odcinkami a płaszczyznami w sześcianie
Kąt nachylenia przekątnej ściany do płaszczyzny innej ściany jest kątem pomiędzy przekątną a krawędzią podstawy, ponieważ to krawędź jest rzutem przekątnej na ścianę sześcianu.
Kąt nachylenia przekątnej sześcianu do płaszczyzny ściany sześcianu jest kątem pomiędzy przekątną sześcianu a przekątną ściany wychodzącą z tego samego wierzchołka, ponieważ przekątna ściany jest rzutem przekątnej sześcianu na ścianę.
Istnieją również inne kąty pomiędzy odcinkami i płaszczyznami w sześcianie.
Obliczymy sinus kąta nachylenia odcinka do płaszczyzny podstawy sześcianu.
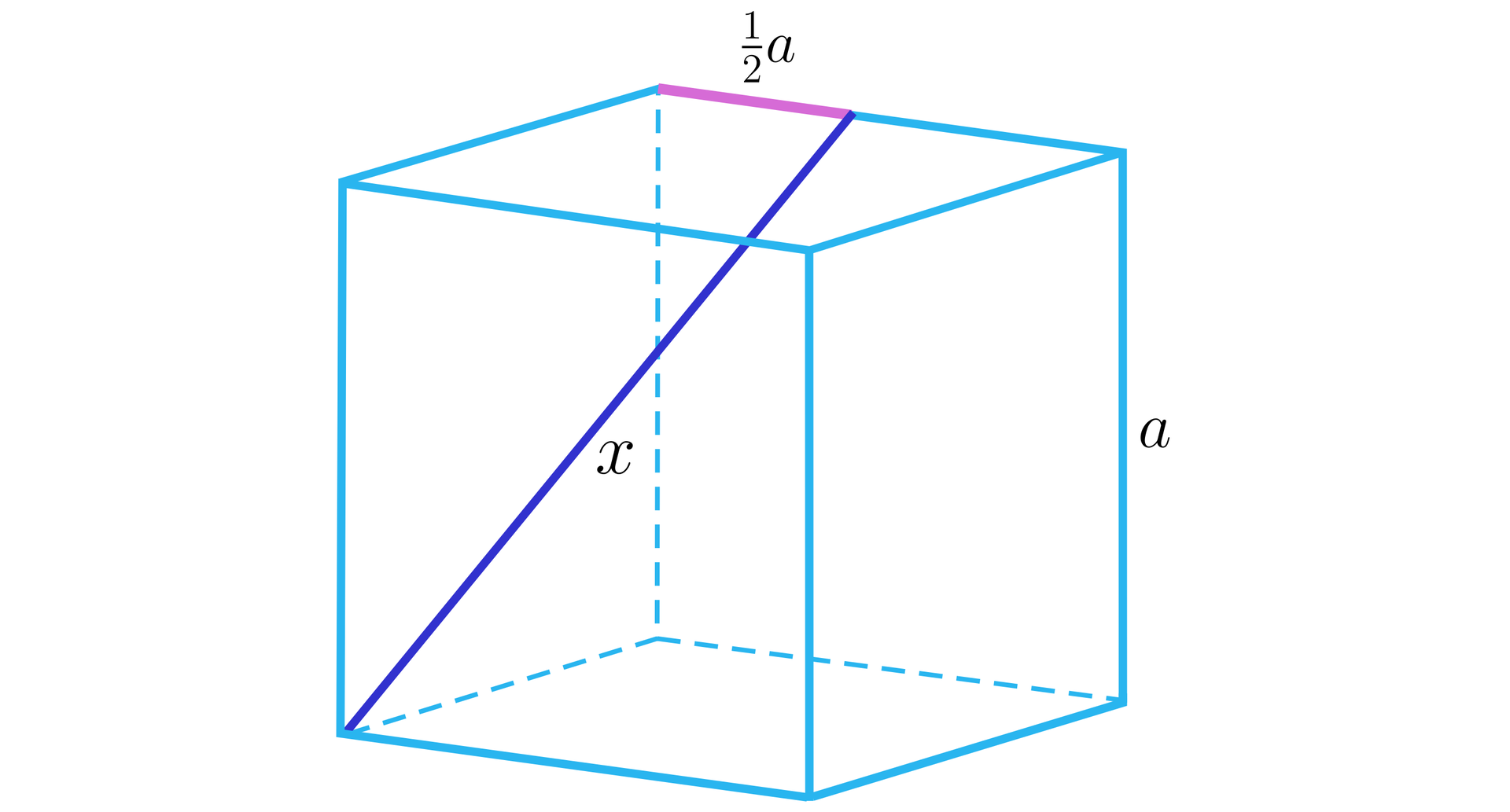
Rozwiązanie
Zaznaczmy kąt nachylenia do płaszczyzny podstawy .
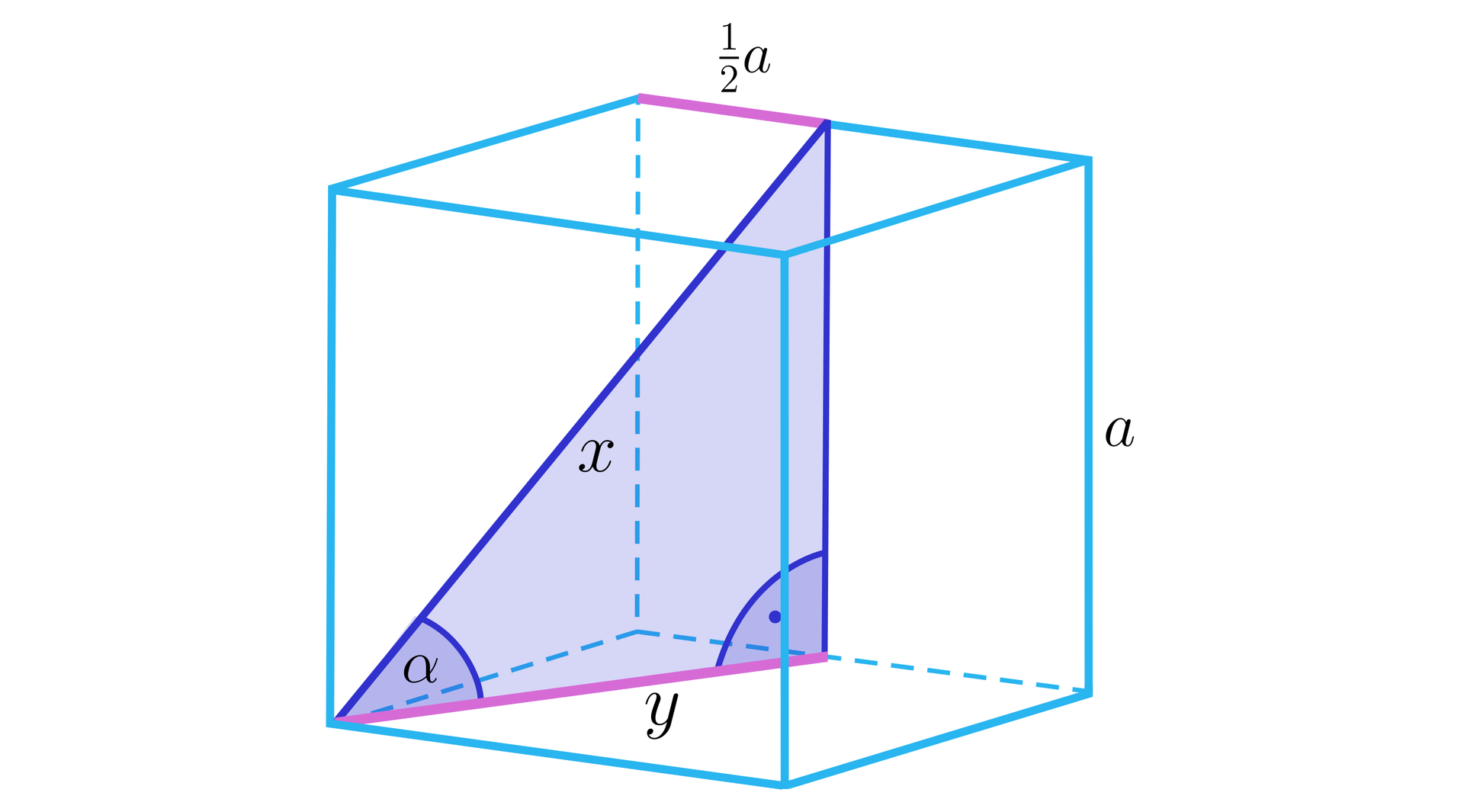
Obliczymy długość odcinka z twierdzenie Pitagorasa:
. A zatem , a stąd .
Teraz wyraźmy długość za pomocą (również z twierdzenia Pitagorasa):
.
A stąd i ostatecznie .
Obliczmy z zależności trygonometrycznych w trójkącie prostokątnym: .
Słownik
kąt pomiędzy przekątną sześcianu, a przekątną ściany wychodzącą z tego samego wierzchołka