Przeczytaj

Wyznaczając zbiór rozwiązań nierówności wymiernej, będziemy korzystać z poniższego twierdzenia.

o równoważności nierówności

Twierdzenie: o równoważności nierówności

$\frac{a}{b} < 0$ wtedy i tylko wtedy, gdy $a b < 0$ i $b \neq 0$ ,

$\frac{a}{b} > 0$ wtedy i tylko wtedy, gdy $a b > 0$ i $b \neq 0$ ,

$\frac{a}{b} \leq 0$ wtedy i tylko wtedy, gdy $a b \leq 0$ i $b \neq 0$
( $\frac{a}{b} \leq 0$ wtedy i tylko wtedy, gdy $a b < 0$ lub $a = 0$ ),

$\frac{a}{b} \geq 0$ wtedy i tylko wtedy, gdy $a b \geq 0$ i $b \neq 0$
( $\frac{a}{b} \geq 0$ wtedy i tylko wtedy, gdy $a b > 0$ lub $a = 0$ ).

Przypomnijmy algorytm rozwiązywania nierówności wymiernych

$I$ sposób

Wyznaczamy dziedzinę nierówności wymiernejdziedzina nierówności wymiernejdziedzinę nierówności wymiernej.
Sprowadzamy nierówność do postaci ogólnej- przenosimy wszystkie wyrażenia na jedną stronę nierówności.
Wykonujemy wskazane działania.
Nierówność wymierną rozwiązujemy doprowadzając ją do równoważnej postaci wielomianowej przy wyznaczonej dziedzinie nierówności wymiernej (zastępujemy iloraz iloczynem z uwzględnieniem założeń).
Wyznaczamy pierwiastki wielomianupierwiastek wielomianupierwiastki wielomianu oraz szkicujemy wykres.
Z wykresu odczytujemy zbiór rozwiązań danej nierówności.
Wyznaczamy rozwiązanie nierówności wymiernej uwzględniając dziedzinę.

$II$ sposób

Wyznaczamy dziedzinę nierówności wymiernejdziedzina nierówności wymiernejdziedzinę nierówności wymiernej.
Mnożymy obustronnie nierówność przez kwadrat mianownika lub przez inne wyrażenia, których znak jest jednoznacznie określony.
Wykonujemy wskazane działania.
Wyznaczamy pierwiastki wielomianu oraz szkicujemy wykres.
Z wykresu odczytujemy zbiór rozwiązań danej nierówności.
Wyznaczamy rozwiązanie nierówności wymiernej uwzględniając dziedzinę.

Rozwiążmy kilka przykładów.

Przykład 1

Wyznaczamy zbiór rozwiązań danej nierównościzbiór rozwiązań danej nierówności $\frac{2 x + 10}{5 - x} \leq 0$ .

Rozwiązanie:

$D = ℝ ∖ \{5\}$ .

Korzystamy z twierdzenia

$\frac{a}{b} \leq 0$ wtedy i tylko wtedy, gdy $a b \leq 0$ i $b \neq 0$ .

Możemy zapisać nierówność wymierną $\frac{2 x + 10}{5 - x} \leq 0$ w postaci równoważnej nierówności iloczynowej

$(2 x + 10) (5 - x) \leq 0$ i $x \neq 5$ ,

$- 2 (x + 5) (x - 5) \leq 0$ i $x \neq 5$ .

Wielomian $W (x) = - 2 (x + 5) (x - 5)$ ma dwa jednokrotne pierwiastki: $(- 5)$ , $5$ .

Uwzględniając dziedzinę nierówności wymiernej $D = ℝ ∖ \{5\}$ szicujemy wykres.

Reop1Ny5bK538

Ilustracja przedstawia poziomą oś z narysowanym wykresem funkcji. Mającym wartości niedodatnie w przedziale od minus nieskończoności do domkniętego minus pięciu i od otwartego pięciu do plus nieskończoności oraz wartości dodatnie w przedziale lewostronnie domkniętym prawostronnie otwartym od minus 5 do pięć.

Zbiorem rozwiązań nierówności jest zbiór $(- \infty; - 5⟩ \cup (5; + \infty)$ .

Następny przykład rozwiążemy na kilka sposobów.

Przykład 2

Podajmy zbiór rozwiązań nierówności $\frac{x^{2}}{- x^{2} - 9} > 3 x$ .

Określamy dziedzinę nierówności wymiernej:

$- x^{2} - 9 \neq 0$ ,

$x^{2} \neq - 9$ ,

czyli $D = ℝ$ .

$I$ sposób rozwiązania nierówności wymiernej

Przekształcamy nierówność do postaci ogólnej

$\frac{x^{2}}{- x^{2} - 9} - 3 x > 0$ ,

$\frac{x^{2} - 3 x (- x^{2} - 9)}{- x^{2} - 9} > 0$ ,

$\frac{x^{2} + 3 x^{3} + 27 x}{- x^{2} - 9} > 0$ ,

Zapisujemy nierówność w postaci równoważnej nierówności iloczynowej

$(x^{2} + 3 x^{3} + 27 x) (- x^{2} - 9) > 0$ ,

$- x (3 x^{2} + x + 27) (x^{2} + 9) > 0$ .

Jedynym jednokrotnym pierwiastkiem wielomianu $W (x) = - x (3 x^{2} + x + 27) (x^{2} + 9)$ jest liczba $0$ .

RTA3F0Y0qwL5v

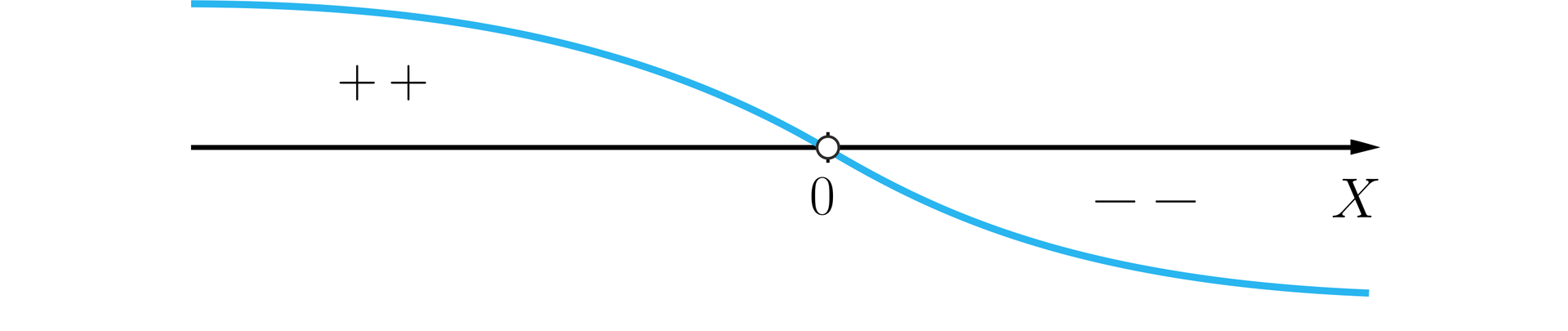
Ilustracja przedstawia poziomą oś z narysowanym wykresem funkcji. Mającym wartości dodatnie w przedziale lewostronnie otwartym prawostronnie otwartym od minus nieskończoności do zera oraz wartości ujemne w przedziale lewostronnie otwartym prawostronnie otwartym od zera do plus nieskończoności.

Na podstawie fragmentu wykresu nierówności wielomianowej odczytujemy zbiór tych wszystkich argumentów, dla których funkcja wielomianowa przyjmuje wartości dodatnie. Zbiorem rozwiązań nierówności wymiernej jest przedział $(- \infty; 0)$ .

$II$ sposób rozwiązania nierówności wymiernej

$\frac{x^{2}}{- x^{2} - 9} > 3 x | \cdot (- x^{2} - 9)$

Daną nierówność wymierną możemy pomnożyć obustronnie przez $(- x^{2} - 9)$ , ponieważ dla każdej liczby rzeczywistej $x$ prawdziwa jest nierówność $(- x^{2} - 9) < 0$ .

Zwrot nierówności zmienia się na przeciwny, ponieważ nierówność mnożymy obustronnie przez wyrażenie ujemne.

Stąd

$x^{2} < 3 x \cdot (- x^{2} - 9)$ ,

$x^{2} < - 3 x^{3} - 27 x$ ,

$3 x^{3} + 27 x + x^{2} < 0$ ,

$x (3 x^{2} + x + 27) < 0$ .

Wielomian $R (x) = x (3 x^{2} + x + 27)$ ma jeden pierwiastek jednokrotny: $0$ .

Współczynnik przy najwyższej potędze zmiennej $x$ jest dodatni.

Szkicujemy fragment wykresu funkcji wielomianowej $y = R (x)$ .

R1FgPvVH2y8Pd

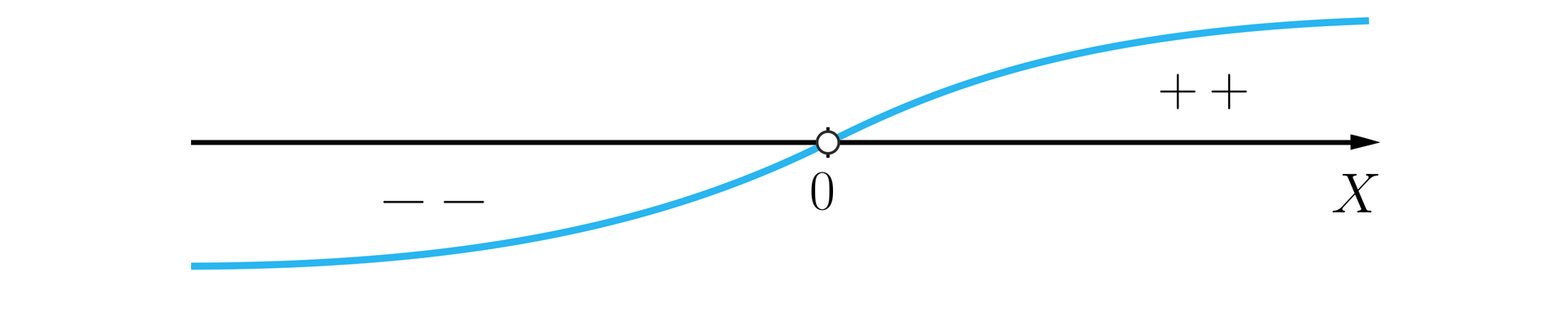
Ilustracja przedstawia poziomą oś z narysowanym wykresem funkcji. Mającym wartości ujemne w przedziale lewostronnie otwartym prawostronnie otwartym od minus nieskończoności do zera oraz wartości dodatnie w przedziale lewostronnie otwartym prawostronnie otwartym od zera do plus nieskończoności.

Zbiorem rozwiązań nierówności $\frac{x^{2}}{- x^{2} - 9} > 3 x$ jest przedział $(- \infty; 0)$ .

$III$ sposób rozwiązania nierówności wymiernej

$\frac{x^{2}}{- x^{2} - 9} > 3 x | \cdot {(- x^{2} - 9)}^{2}$

Daną nierówność możemy pomnożyć obustronnie przez ${(- x^{2} - 9)}^{2}$ .

Wyrażenie ${(- x^{2} - 9)}^{2}$ jest dodatnie dla każdej liczby ze zbioru $D = ℝ$ .

Zwrot nierówności pozostanie bez zmiany, ponieważ nierówność mnożymy obustronnie przez wyrażenie dodatnie.

Wówczas

$\frac{x^{2}}{- x^{2} - 9} \cdot {(- x^{2} - 9)}^{2} > 3 x \cdot {(- x^{2} - 9)}^{2}$ ,

$x^{2} \cdot (- x^{2} - 9) > 3 x \cdot {(- x^{2} - 9)}^{2}$ .

Przenieśmy wszystkie wyrażenia na jedną stronę nierówności

$x^{2} \cdot (- x^{2} - 9) - 3 x \cdot {(- x^{2} - 9)}^{2} > 0$ .

Wyłączmy $x \cdot (- x^{2} - 9)$ przed nawias.

Zatem

$x \cdot (- x^{2} - 9) [x - 3 (- x^{2} - 9)] > 0$

$x \cdot (- x^{2} - 9) (3 x^{2} + x + 27) > 0$ .

Jedynym jednokrotnym pierwiastkiem wielomianu $S (x) = x \cdot (- x^{2} - 9) (3 x^{2} + x + 27)$ jest liczba $0$ .

Poniżej przedstawmy fragment wykresu funkcji wielomianowej $y = S (x)$ .

RFAgVsgoWR2ne

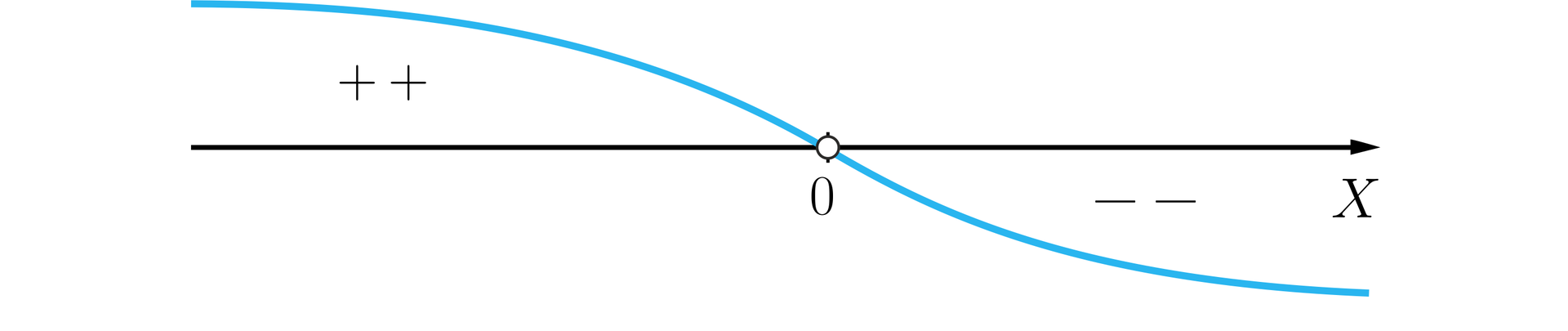
Odczytujemy zbiór tych wszystkich argumentów, dla których funkcja wielomianowa przyjmuje wartości dodatnie.

Zbiorem rozwiązań nierówności jest przedział $(- \infty; 0)$ .

Warto zauważyć, że zbiór rozwiązań danej nierówności jest taki sam, mimo zastosowania kilku sposobów rozwiązania zadania.

Przykład 3

Wyznacz zbiór rozwiązań nierówności $\frac{2 x - 1}{x^{3} - 3 x^{2}} \geq \frac{x - 2}{x^{3} + x^{2}}$ .

Założenie: $x^{3} - 3 x^{2} \neq 0$ , $x^{3} + x^{2} \neq 0$

$x^{2} (x - 3) \neq 0$ , $x^{2} (x + 1) \neq 0$

$x \neq 0$ , $x \neq 3$ , $x \neq - 1$ .

$D = ℝ ∖ \{- 1; 0; 3\}$ .

Rozkładamy na czynniki wyrażenia występujące w mianowniku

$\frac{2 x - 1}{x^{2} (x - 3)} \geq \frac{x - 2}{x^{2} (x + 1)}$ .

Pomnóżmy obie strony nierówności przez $x^{2}$ .

Wyrażenie $x^{2}$ jest dodatnie dla każdej liczby ze zbioru $D$ .

Zwrot nierówności pozostaje bez zmiany

$\frac{2 x - 1}{x - 3} \geq \frac{x - 2}{x + 1}$ .

Sprowadźmy nierówność do postaci ogólnej

$\frac{2 x - 1}{x - 3} - \frac{x - 2}{x + 1} \geq 0$ ,

$\frac{(2 x - 1) (x + 1) - (x - 2) (x - 3)}{(x - 3) (x + 1)} \geq 0$ ,

$\frac{2 x^{2} + x - 1 - (x^{2} - 5 x + 6)}{(x - 3) (x + 1)} \geq 0$ ,

$\frac{2 x^{2} + x - 1 - x^{2} + 5 x - 6}{(x - 3) (x + 1)} \geq 0$ ,

$\frac{x^{2} + 6 x - 7}{(x - 3) (x + 1)} \geq 0$ .

Korzystamy z twierdzenia

$\frac{a}{b} \geq 0$ wtedy i tylko wtedy, gdy $a b \geq 0$ i $b \neq 0$ .

Inaczej zapisujemy nierówność w postaci równoważnej nierówności iloczynowej

$(x^{2} + 6 x - 7) (x - 3) (x + 1) \geq 0$ ,

$(x + 7) (x - 1) (x - 3) (x + 1) \geq 0$ .

Wielomian $W (x) = (x + 7) (x - 1) (x - 3) (x + 1)$ ma cztery pierwiastki jednokrotne: $(- 7)$ , $(- 1)$ , $1$ , $3$ .

Współczynnik przy najwyższej potędze zmiennej $x$ jest dodatni.

Uwzględniając dziedzinę nierówności wymiernej $D = ℝ ∖ \{- 1; 0; 3\}$ szkicujemy wykres.

R4qePQouUIZvd

Ilustracja przedstawia poziomą oś z narysowanym wykresem funkcji. Mającym wartości niedodatnie w przedziale lewostronnie domkniętym prawostronnie otwartym od minus 7 do minus jeden oraz w przedziale lewostronnie domkniętym prawostronnie otwartym od 1 do trzech. Wartości nieujemne w przedziałach lewostronnie otwartym prawostronnie domkniętym od minus nieskończoności do minus siedmiu, w przedziale lewostronnie otwartym prawostronnie domkniętym od minus 1 do jedynki oraz w przedziale lewostronnie otwartym prawostronnie otwartym od 3 do plus nieskończoności.

Odczytujemy zbiór argumentów, dla których funkcja wielomianowa przyjmuje wartości nieujemne.

Zbiorem rozwiązań nierówności wymiernej $\frac{2 x - 1}{x^{3} - 3 x^{2}} \geq \frac{x - 2}{x^{3} + x^{2}}$ jest zbiór $(- \infty; - 7⟩ \cup (- 1; 0) \cup (0; 1⟩ \cup (3; + \infty)$ .

Słownik

zbiór rozwiązań nierówności z jedną niewiadomą

każda liczba rzeczywista, która spełnia tę nierówność.

dziedzina nierówności wymiernej

dziedziną nierówności wymiernej są wszystkie liczby rzeczywiste za wyjątkiem pierwiastków wielomianu $W_{2} (x)$ znajdującego się w mianowniku danego wyrażenia $\frac{W_{1} (x)}{W_{2} (x)}$

$D = ℝ ∖ \{x : W_{2} (x) = 0\}$

pierwiastek wielomianu

pierwiastkiem wielomianu $W (x)$ nazywamy liczbę rzeczywistą $a$ , dla której $W (a) = 0$

Wprowadzenie

Animacja

$I$ sposób

$II$ sposób

Słownik

Wprowadzenie

Animacja

Przeczytaj

I sposób

II sposób

Słownik

$I$ sposób

$II$ sposób