Skala podobieństwa sześcianów wynosi $\frac{4}{7}$. Obliczymy długość przekątnej większego sześcianu wiedząc, że krawędź podstawy mniejszego z nich ma długość $8 \mathrm{cm}$.

Rozwiązanie

Niech $a$ – długość boku większego sześcianu. Układamy równanie, wykorzystując skalę podobieństwa brył:

$\frac{4}{7}=\frac{8}{a}$,

$a=\frac{56}{4}=14$.

Zatem przekątna sześcianu ma długość $14\sqrt{3}\mathrm{cm}$.

Dwa czworościany foremne są podobnefigury podobnepodobne w skali $k=\frac{7}{12}$ . Obliczmy wysokość większego z nich, jeśli krawędź mniejszego ma długość $a$.

Rozwiązanie

Zacznijmy od obliczenia wysokości czworościanu foremnego o krawędzi $a$.

Oznaczmy ją $H$.

$H^2+{\left(\frac{a\sqrt{3}}{3}\right)}^2=a^2$

$H^2=\frac{2}{3}{a}^2$

$H=\frac{a\sqrt{6}}{3}$

Oznaczmy $H\text{'}$ wysokość większego czworościanu foremnego. Wówczas mamy:

$\frac{{\displaystyle \frac{a\sqrt{6}}{3}}}{H\text{'}}=\frac{7}{12}$,

$H\text{'}=\frac{4}{7}a\sqrt{6}$.

Wysokość większego czworościanu foremnego ma długość $\frac{4}{7}a\sqrt{6}$.

Dane są dwa podobne stożki. Skala podobieństwa pól ich podstaw wynosi $\frac{9}{16}$. Jaka jest skala podobieństwa tych stożków?

Rozwiązanie

Skala podobieństwa pól figur płaskich wynosi $k^2$.

$k^2=\frac{9}{16}$

$k=\frac{3}{4}$

Stosunek promieni kół wynosi $\frac{3}{4}$, więc skala podobieństwa stożków wynosi tyle samo.

Dane są dwa ostrosłupy prawidłowe czworokątne. W jednym krawędź boczna o długości $10 \mathrm{cm}$ jest nachylona do płaszczyzny podstawy pod kątem $45°$, w drugim ściana boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens wynosi $\sqrt{2}$, a wysokość jego ściany bocznej ma długość $10\sqrt{3}$. Sprawdź, czy te ostrosłupy są podobne. Jeśli tak, podaj ich skalę podobieństwa.

Rozwiązanie:

Wykonajmy rysunki pomocnicze.

RZwEiIt0BRp9g

Ilustracja przedstawia ostrosłup prawidłowy czworokątny, długość krawędzi podstawy wynosi a. Długość krawędzi bocznej wynosi dziesięć. W podstawie zaznaczono jej przekątne. Spodek wysokości H opuszczonej z wierzchołka górnego znajduje się w miejscu przecięcia przekątnych. W ostrosłupie zaznaczono trójkąt prostokątny, którego przeciwprostokątną jest krawędź boczna, a przyprostokątnymi są wysokość ostrosłupa i odcinek będący fragmentem przekątnej podstawy łączący wysokość z przeciwprostokątną. Kąt pomiędzy przekątną podstawy a krawędzią boczną wynosi 45 stopni.

Zauważmy, że zaznaczony trójkąt jest równoramiennym trójkątem prostokątnym. Wówczas $10=H\sqrt{2}$, czyli $H=5\sqrt{2}$.

Połowa przekątnej podstawy też ma długość $5\sqrt{2}$, cała przekątna więc ma długość $10\sqrt{2}$, co oznacza, że krawędź podstawy możemy obliczyć z zależności: $10\sqrt{2}=a\sqrt{2}$, stąd $a=10$.

Narysujmy teraz drugi omawiany ostrosłup.

RJ1jnoxo6OeSD

Ilustracja przedstawia ostrosłup prawidłowy czworokątny, długość krawędzi podstawy wynosi a. W podstawie zaznaczono jej przekątne. Spodek wysokości opuszczonej z wierzchołka górnego znajduje się w miejscu przecięcia przekątnych. Wysokość ma długość $\sqrt{2}x$ . W ścianie bocznej ostrosłupa również zaznaczono jej wsokość ma ona długość $10\sqrt{3}$. W ostrosłupie zaznaczono trójkąt prostokątny, którego przeciwprostokątną jest wysokość ściany bocznej, a przyprostokątnymi są wysokość ostrosłupa i odcinek łączący spodki tych wysokości, który podpisano literą x. Kąt pomiędzy wysokością ściany bocznej, a odcinkiem łączącym spodki wysokości podpisano literą alfa.

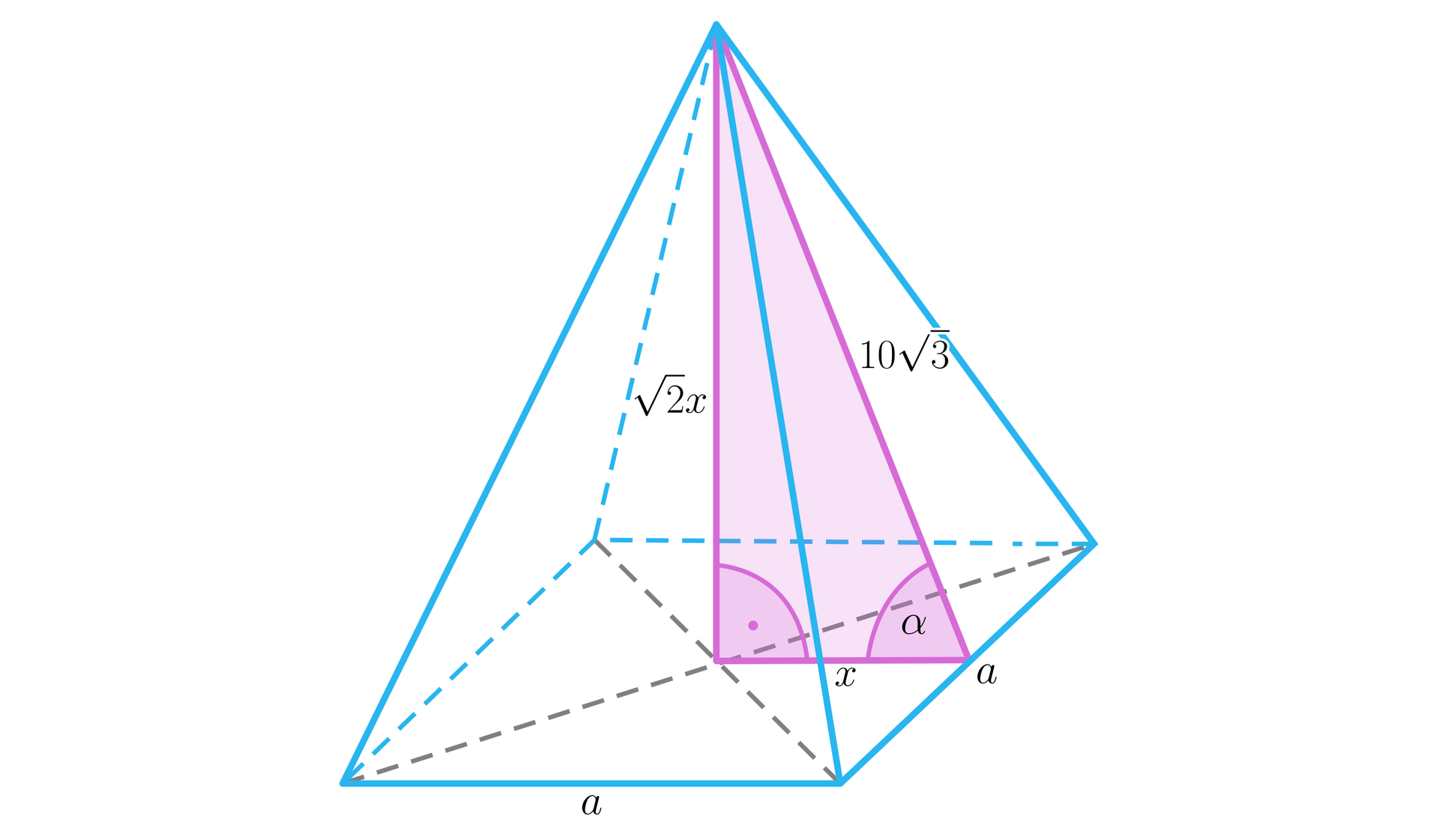
Z twierdzenia Pitagorasa obliczmy $x$.

${\left(\sqrt{2}x\right)}^2+x^2={\left(10\sqrt{3}\right)}^2$

$2x^2+x^2=300$

$3x^2=300$

$x^2=100$

$x=10$

Zatem krawędź podstawy ostrosłupa ma długość $a=20$, a wysokość ostrosłupa ma długość $10\sqrt{2}$.

Porównajmy odpowiednie odcinki w obu ostrosłupach:

$\frac{10}{20}=\frac{5\sqrt{2}}{10\sqrt{2}}$,

$100\sqrt{2}=100\sqrt{2}$.

Zatem ostrosłupy są podobne. Skala podobieństwa wynosi $\frac{1}{2}$.

Dane są dwa stożki. W jednym kąt rozwarcia stożka jest prosty, a promień podstawy ma długość $r$. W drugim sinus kąta nachylenia tworzącej, o długości $2r$, do płaszczyzny podstawy wynosi $\frac{1}{2}$.

Sprawdzimy, czy te stożki są podobne. Jeśli tak, podamy ich skalę podobieństwa.

Rozwiązanie:

Wykonajmy rysunki pomocnicze.

Rk9U0Dni9U5U4

Ilustracja przedstawia trójkąt prostokątny ABS, przyprostokątne AS oraz BS są podpisane literą l. Odcinek AB podpisano $2r$. Przez punkty A oraz B przechodzi okrąg.

Trójkąt $ABS$ jest trójkątem prostokątnym równoramiennym, więc $2r=l\sqrt{2}$, stąd orzymujemy $l=\frac{2r}{\sqrt{2}}=\frac{2r\sqrt{2}}{2}=r\sqrt{2}$.

Narysujmy drugi stożek.

RAeiBpNFRkN7i

Ilustracja przedstawia trójkąt ABS, bok BS podpisano $2r$. W trójkącie z wierzchołka S na bok AB opuszczono wysokość H. Przez punkty A oraz B przechodzi okrąg. Odcinek od spodka wysokości do wierzchołka podpisano literą x. Kąt ABS popisano literą alfa.

Skoro $\sin \alpha =\frac{1}{2}$, to znaczy, że $\frac{H}{2r}=\frac{1}{2}$, czyli $H=r$.

Policzmy promień podstawy:

$x^2={\left(2r\right)}^2-r^2$

$x^2=3r^2$

$x=r\sqrt{3}$.

Porównajmy odpowiednie odcinki w obu stożkach:

$\frac{r}{r\sqrt{2}}=\frac{r\sqrt{3}}{2r}$

$2r^2\ne r^2\sqrt{6}$

Zatem stożki nie są podobne.

jeżeli dane są cztery odcinki $a,b,c,d$ takie, że stosunek pierwszych dwóch $\left(a:b\right)$ jest równy stosunkowi dwóch ostatnich $\left(c:d\right)$, to takie odcinki nazywamy proporcjonalnymi i wyrażamy to, pisząc proporcję

w uproszczeniu możemy powiedzieć, że ich iloraz jest stały

figury, których odpowiadające sobie odcinki są proporcjonalne