Przeczytaj
Dwie bryły są podobne, jeśli odległości między punktami jednej bryły są proporcjonalne do odległości między odpowiednimi punktami drugiej bryły.
Stosunek odległości między odpowiednimi punktami brył podobnychpodobnych nazywamy skalą podobieństwa.
Rozpatrzymy teraz dwa sześciany o krawędziach długości odpowiednio i .

Są to bryły podobne. Ich skala podobieństwa wynosi .
Policzymy ich pola powierzchni całkowitej.
Stosunek pól mniejszej bryły do większej wynosi więc:
.
Jeśli skala podobieństwa brył podobnych jest równa , to stosunek pól powierzchni tych brył jest równy .
Dane są dwa sześciany. Pole powierzchni pierwszego z nich jest dziewięciokrotnie większe od pola powierzchni drugiego. Jaka jest skala podobieństwa większego z tych sześcianów do mniejszego?
Rozwiązanie
Z zadania wiemy, że stosunek pól powierzchni sześcianów wynosi , zatem jeśli skalę podobieństwa oznaczymy , to możemy zapisać równanie:
.
Zatem sześciany są podobne w skali .
Dane są dwie kule. Pole pierwszej z nich wynosi . Druga kula ma promień dwa razy dłuższy niż pierwsza kula. Obliczymy pole drugiej kuli.
Rozwiązanie
Skoro promień drugiej kuli jest dwa razy większy od promienia pierwszej kuli, tzn. że skala podobieństwa tych brył wynosi . Zatem stosunek ich pól wynosi .
Pole drugiej kuli (oznaczmy ) wynosi więc ,
czyli .
Dane są dwa podobne stożki. Pole powierzchni całkowitej większego z nich jest o większe od pola powierzchni całkowitej mniejszego z nich. Obliczymy wysokość większego stożka, jeśli wysokość mniejszego wynosi .
Rozwiązanie
Oznaczmy pole powierzchni mniejszego stożka jako . Wówczas pole większego z nich wynosi
.
Zatem stosunek pól wynosi , czyli .
Obliczmy więc wysokość większego stożka:
.
Uzasadnimy, że stożek o promieniu długości i polu powierzchni jest podobny do stożka o wysokości długości i objętości . Podamy skalę podobieństwa większego stożka do mniejszego.
Rozwiązanie
Obliczmy niezbędne długości w obydwu stożkach.
Stożek nr 1.
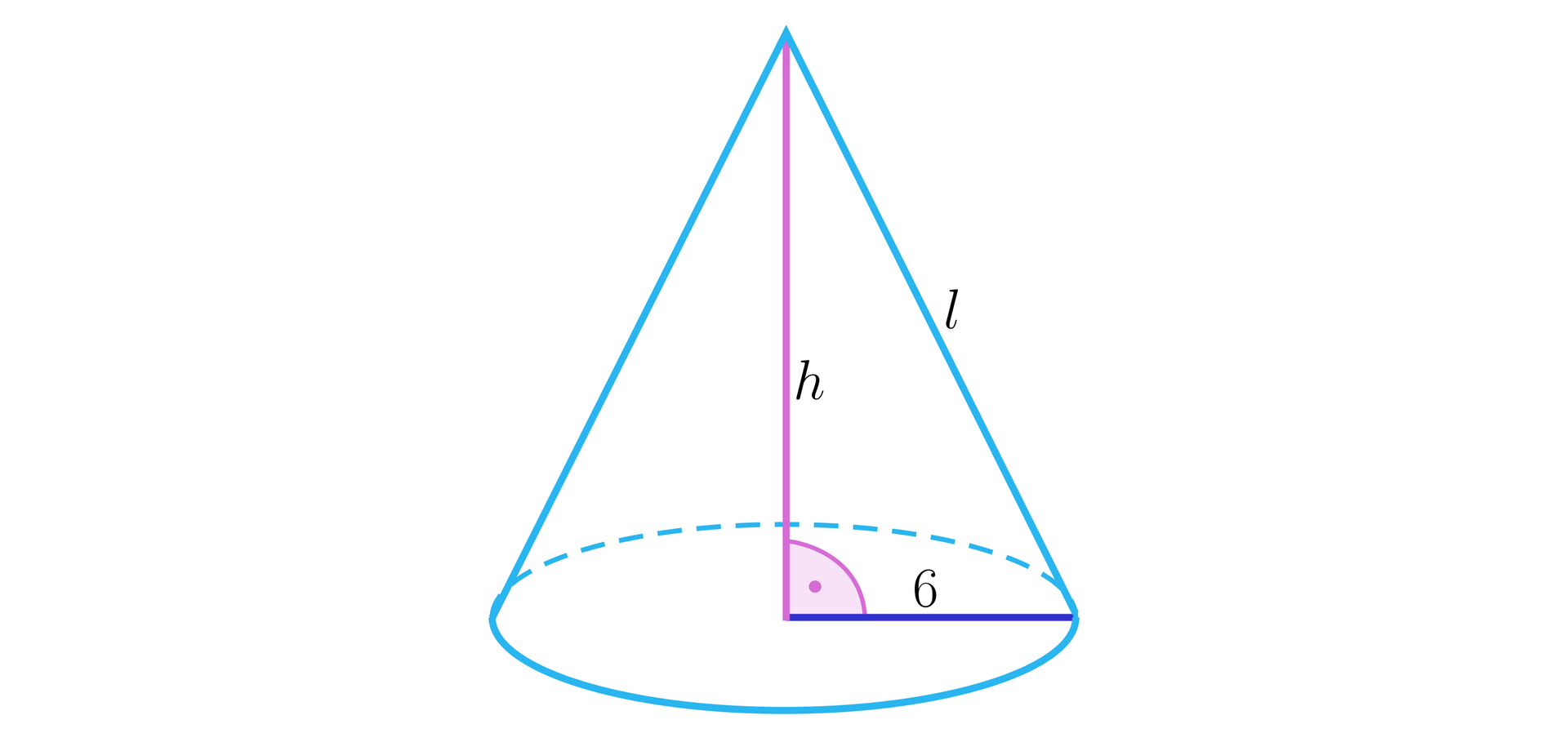
Stożek nr 2.

Analizując długości poszczególnych odcinkówodcinków w stożkach zauważamy, że są one proporcjonalne. Wszystkie odcinki w drugim stożku są razy krótsze. Zatem skala podobieństwa .
Na rysunkach przedstawiono dwa ostrosłupy prawidłowe sześciokątne. Wiadomo, że , . Pokażemy, że są to bryły podobne oraz obliczymy skalę podobieństwa oraz stosunek pól podstaw obu brył.

Rozwiązanie
Aby porównać odpowiednie odcinki w ostrosłupach, musimy je obliczyć. Zajmijmy się każdym ostrosłupem z osobna.

Wiemy, że , więc z jedynki trygonometrycznej otrzymujemy równanie:
, .
Krótsza przekątna podstawy ma długość , zatem sześciokąt foremny ma bok długości:
.
Oznaczmy krawędzie boczne jako . Wówczas z twierdzenia cosinusów otrzymujemy:
.
Zajmijmy się teraz drugim ostrosłupem:

Wysokość ostrosłupa ma długość
.
Oznaczmy krawędzie boczne jako . Wówczas
.
Porównajmy teraz odpowiednie odcinki w naszych ostrosłupach:
długości krawędzi podstawy:
długosci krawędzi bocznych:
Wniosek: ostrosłupy są podobne w skali , co oznacza, że ich pola powierzchni są w stosunku .
Na rysunku przedstawiono ostrosłup prawidłowy trójkątny o krawędzi podstawy i kącie przy wierzchołku ostrosłupa o mierze . Obliczymy pole powierzchni ostrosłupa czterokrotnie mniejszego.

Rozwiązanie
Obliczmy pole powierzchni wyjściowego ostrosłupa. Oznaczmy krawędzie boczne jako . Wówczas z twierdzenia cosinusów otrzymujemy:
Pole ściany bocznej możemy policzyć ze wzoru .
Zatem:
.
Mamy trzy ściany boczne, więc pole powierzchni bocznej wynosi:
.
Policzmy pole podstawy. Jest to trójkąt równoboczny o podstawie długości .
.
Pole powierzchni całkowitej ostrosłupa:
.
Drugi ostrosłup jest czterokrotnie mniejszy, czyli skala podobieństwa brył wynosi . Zatem stosunek ich pól wynosi , co oznacza, że pole powierzchni drugiego ostrosłupa jest razy mniejsze od pola powierzchni ostrosłupa wyjściowego. Pole powierzchni ostrosłupa podobnego do naszego ostrosłupa wyjściowego wynosi więc:
.
Słownik
jeżeli dane są cztery odcinki takie, że stosunek pierwszych dwóch jest równy stosunkowi dwóch ostatnich , to takie odcinki nazywamy proporcjonalnymi i wyrażamy to, pisząc proporcję
w uproszczeniu możemy powiedzieć, że ich iloraz jest stały
mają ten sam kształt, ale mogą mieć inną wielkość