Przeczytaj

W tym materiale skupimy się na obliczaniu pola powierzchni ostrosłupa trójkątnego.

Ostrosłup trójkątny, to taki ostrosłup, którego podstawą jest trójkąt. Ściany boczne ostrosłupa są trójkątami o wspólnym wierzchołku zwanym wierzchołkiem ostrosłupa. Ostrosłup trójkątny jest inaczej nazywany czworościanem.

Wśród ostrosłupów możemy wyróżnić ostrosłupy proste oraz pochyłe.

Ostrosłup nazywamy ostrosłupem trójkątnym prostym, jeśli spodek wysokościspodek wysokości bryłyspodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na trójkącie będącym jego podstawą. Ostrosłup prosty ma wszystkie krawędzie boczne równej długości.

R15eDM62oVhaA

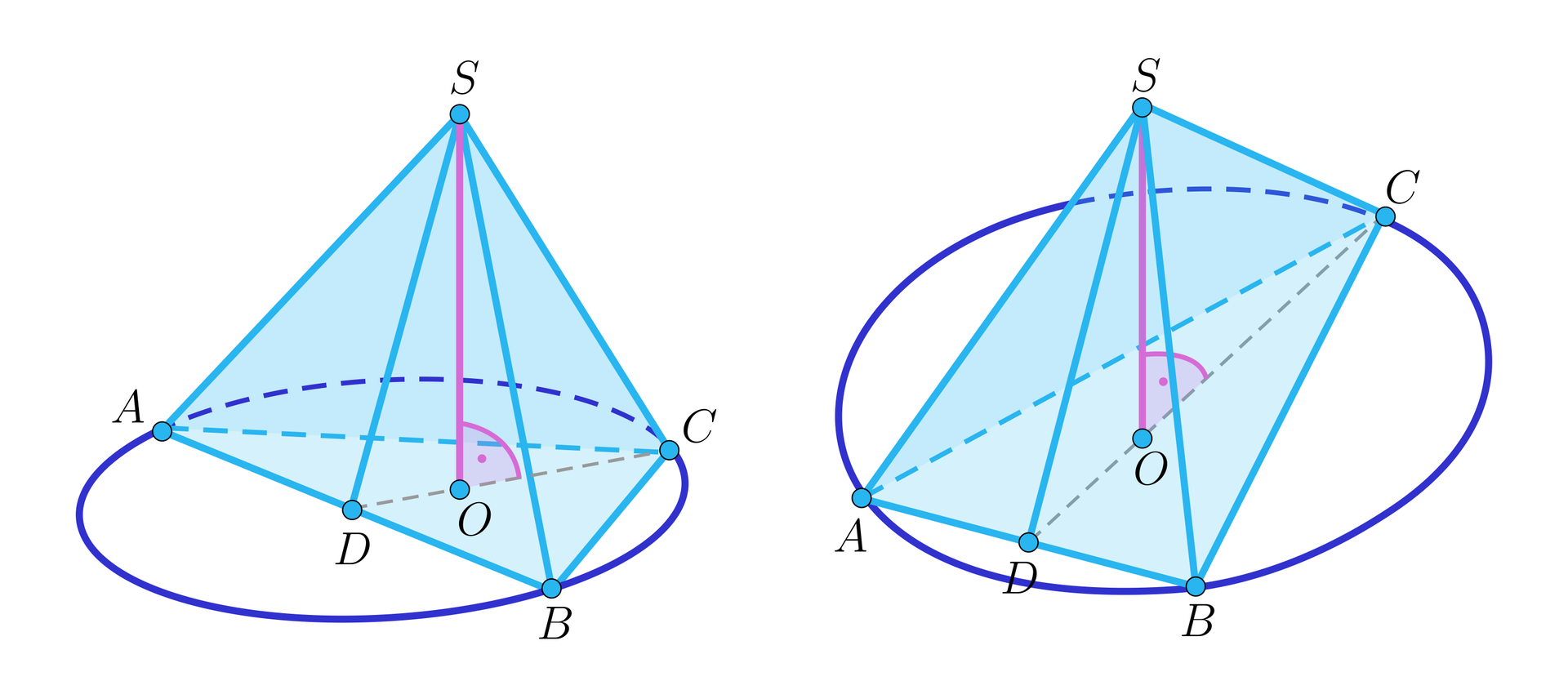
Ilustracja przedstawia dwa rysunku obok siebie. Z lewej strony mamy ostrosłup A B C S, którego podstawia jest trójkątem A B C wpisanym w okrąg. Zaznaczono odcinek S D będący wysokością ściany A B S oraz zaznaczono wysokość bryły S O. Po prawej stronie analogiczny rysunek, przy czym trójkąt A B C będący podstawą, ma inny kształt, niż na pierwszym rysunku. Oznaczenia są niezmienione.

Ostrosłup trójkątny pochyły nie spełnia opisanej powyżej własności, często spodek wysokości ostrosłupa znajduje się poza podstawą ostrosłupa.

RTK1cMjAgkyWf

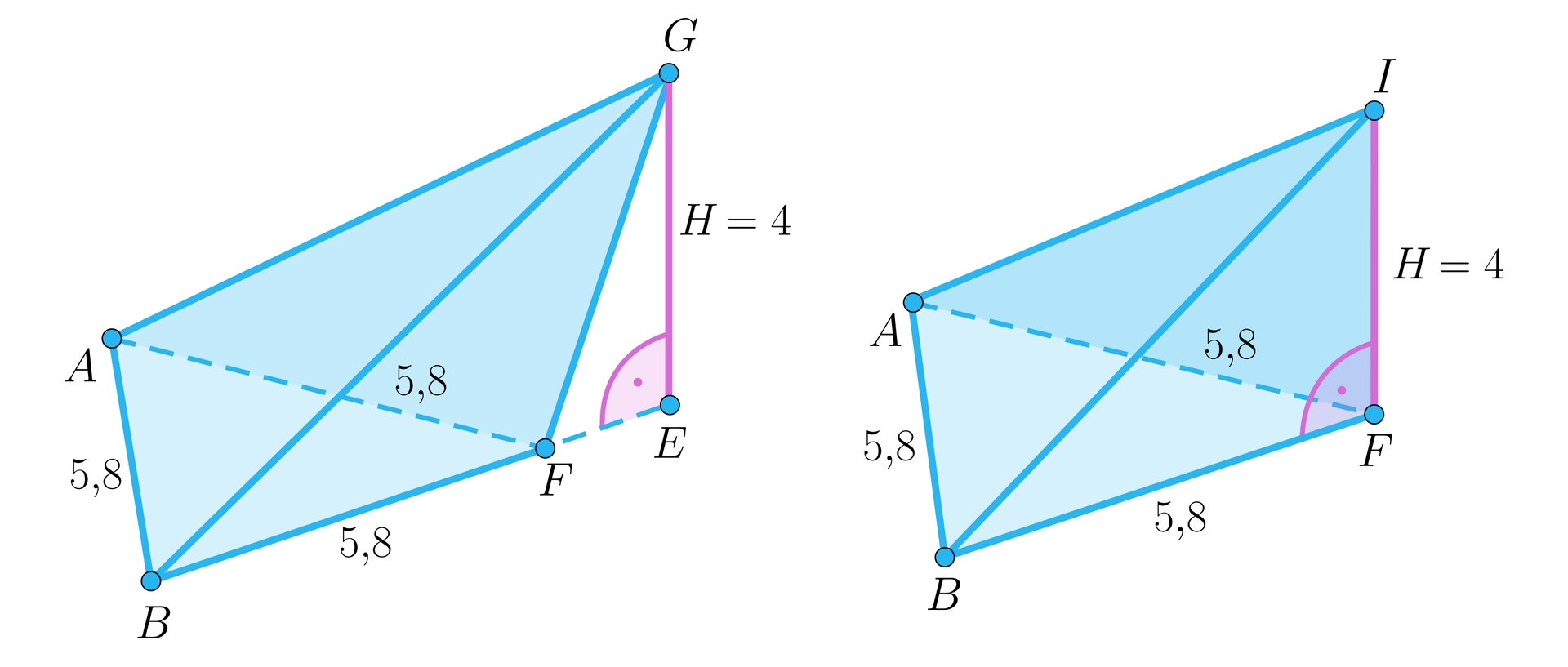
Ilustracja przedstawia dwa warianty ostrosłupa pochyłego. Po lewej stronie mamy ostrosłup A B F G, którego wszystkie krawędzie ścian są pochyłe. W podstawie bryły znajduje się trójkąt równoboczny A B F o boku o długości 5,8; krawędź podstawy B F przedłużono i na to przedłużenie upuszczono wysokość bryły H równą 4, która jest odcinkiem G E, gdzie punkt E leży poza bryłą. Drugi wariant bryły ma wierzchołki A B F I. Podstawą bryły jest trójkąt równoramienny A B F o boku o długości 5,8 , przy czym dwie z krawędzi ścian są pochyłe: A I oraz B I, natomiast krawędź ściany F I jest prostopadła do płaszczyzny podstawy. Krawędź ta jest jednocześnie wysokością bryły H równą 4

Jeśli wszystkie krawędzie boczne ostrosłupa tworzą z podstawą kąty równej miary, to spodek wysokości jest jednakowo oddalony od wierzchołków podstawy jest, więc środkiem okręgu opisanego na podstawie.

Jeśli wszystkie ściany boczne tworzą z podstawą kąty równej miary, to spodek wysokości jest jednakowo oddalony od krawędzi podstawy jest, więc środkiem okręgu wpisanego w podstawę.

Pole powierzchni ostrosłupa to suma pola podstawy i pola powierzchni bocznej.

P = P_{p} + P_{b}

$P_{p}$ – pole podstawy

$P_{b}$ – pole powierzchni bocznej, czyli suma wszystkich pól ścian bocznych ostrosłupa

Dla czworościanu foremnegoczworościan foremnyczworościanu foremnego o krawędzi $a$ :

Pole powierzchni $P = a^{2} \sqrt{3}$ .

Przykład 1

Podstawą ostrosłupa prostego jest trójkąt prostokątny równoramienny, którego ramię ma długość $6 \sqrt{2}$ . Wiedząc, że wysokość ostrosłupa ma długość $8 cm$ , oblicz długości krawędzi bocznych oraz pole powierzchni całkowitej ostrosłupa.

Rozwiązanie:

Wiemy, że ostrosłup jest prosty, więc spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na jego podstawie. W tym przypadku jest to środek przeciwprostokątnej, bo podstawą jest trójkąt prostokątny.

Wykonujemy rysunek z odpowiednimi oznaczeniami.

R1F0EcFIwaaRU

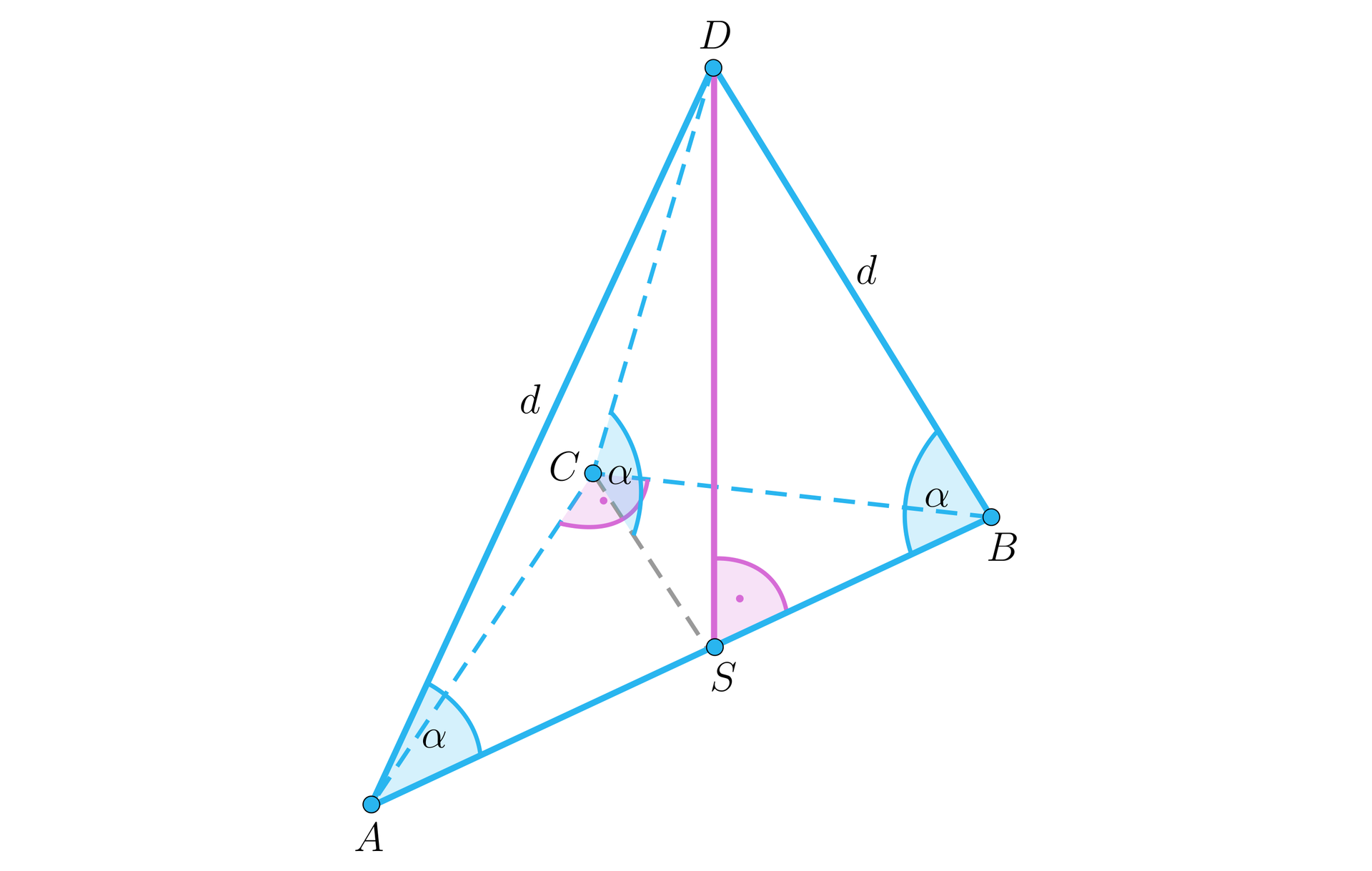
Ilustracja przedstawia ostrosłup, którego podstawą jest trójkąt prostokątny A B C, jego przeciwprostokątną jest bok AB. Wierzchołek górny podpisano literą D. Krawędź boczna ostrosłupa jest podpisana literą d. Z wierzchołka D na krawędź AB opuszczono wysokość, której spodek podpisano literą S. Punkty CS połączono linią przerywaną. Kąty DCS, DAS oraz DBS podpisano literą alfa.

Wiemy, że $|A C| = |B C| = 6 \sqrt{2}$ są długościami ramion trójkąta prostokątnego w podstawie, więc $|A B| = 12$ oraz długość wysokości ostrosłupa $|S D| = 8$ , $|A S| = \frac{1}{2} |A B| = 6$ .

Zauważmy, że $|A D| = |B D| = |C D|$ , ponieważ ostrosłup jest prosty. Oznaczmy $|A D| = d$ .

Punkt $S$ jest spodkiem wysokości ostrosłupa, odcinek $S D$ jest prostopadły do $A S$ i $S B$ i $S C$ . Długość krawędzi bocznej obliczymy korzystając z trójkąta $A S D$ i twierdzenia Pitagorasa

${|A S|}^{2} + {|S D|}^{2} = {|A D|}^{2}$

$6^{2} + 8^{2} = d^{2}$

$d^{2} = 100$

$d = 10$

Obliczamy pole podstawy ostrosłupa:

$P_{p} = \frac{1}{2} \cdot {(6 \sqrt{2})}^{2} = 36$

Mamy już pole podstawy, obliczymy pole powierzchni bocznej, która jest sumą pól ścian bocznych ostrosłupa. W tym celu obliczymy pola odpowiednio trójkątów $A B D$ , $A C D$ i $C B D$ .

$P_{A B D} = \frac{1}{2} \cdot |A B| \cdot |D S| = \frac{1}{2} \cdot 12 \cdot 8 = 48$

Trójkąty $A C D$ i $C B D$ są przystające oraz równoramienne.

R1KuZUajWA90F

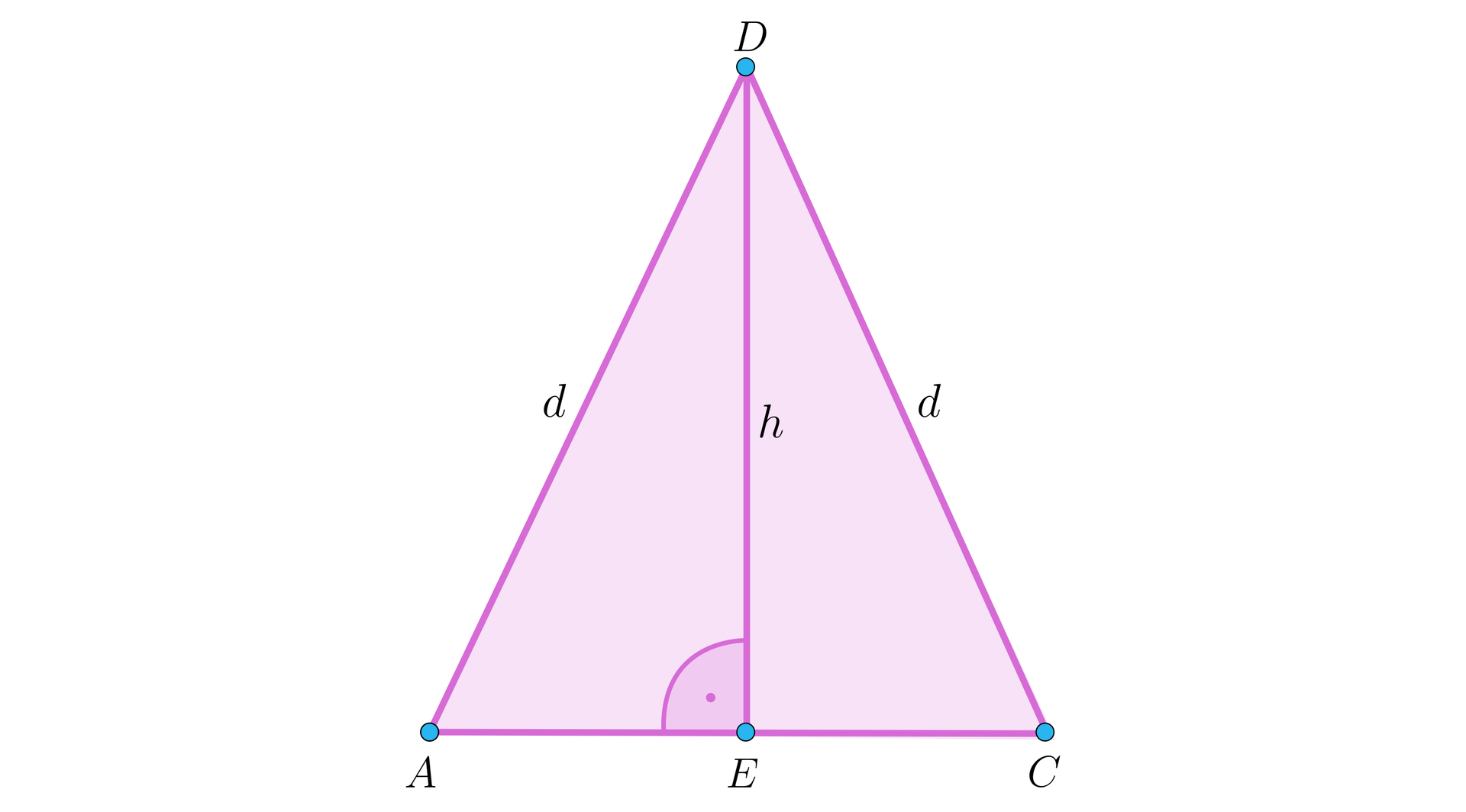
Ilustracja przedstawia trójkąt A C D, jego ramiona AD oraz CD są popisane literą d. Z wierzchołka D na podstawę AC opuszczono wysokość h, której spodek podpisano literą E.

Korzystając z rysunku pomocniczego obliczymy długość $h$ wysokości trójkąta
$A C D$ .

Odcinek $A E$ jest połową $A C$ i jego długość wynosi $|A E| = 3 \sqrt{2}$ .

Na podstawie twierdzenia Pitagorasa dla trójkąta $A E D$ mamy:

${|A E|}^{2} + {|E D|}^{2} = {|A D|}^{2}$

${(3 \sqrt{2})}^{2} + h^{2} = 10^{2}$

$h^{2} = 100 - 18$

$h = \sqrt{82}$

$P_{A C D} = \frac{1}{2} \cdot |A C| \cdot |E D| = \frac{1}{2} \cdot 6 \sqrt{2} \cdot \sqrt{82} = 6 \sqrt{41}$

Obliczymy pole powierzchni bocznej:

$P_{b} = P_{A B D} + P_{C B D} + P_{A C D} = 48 + 2 \cdot 6 \sqrt{41} = 48 + 12 \sqrt{41}$

Zatem pole powierzchni ostrosłupa:

$P = P_{p} + P_{b} = 36 + 48 + 12 \sqrt{41} = 84 + 12 \sqrt{41} = 12 (7 + \sqrt{41})$

Przykład 2

Podstawą ostrosłupa $A B C D$ jest trójkąt równoboczny $A B C$ o boku długości $16$ . Dwie ściany boczne są prostopadłe do podstawy, a trzecia tworzy z podstawą kąt o mierze $60 °$ . Oblicz pole powierzchni całkowitej ostrosłupa $A B C D$ .

Rozwiązanie:

Wykonujemy rysunek z odpowiednimi oznaczeniami.

RFekAC1gzuYSf

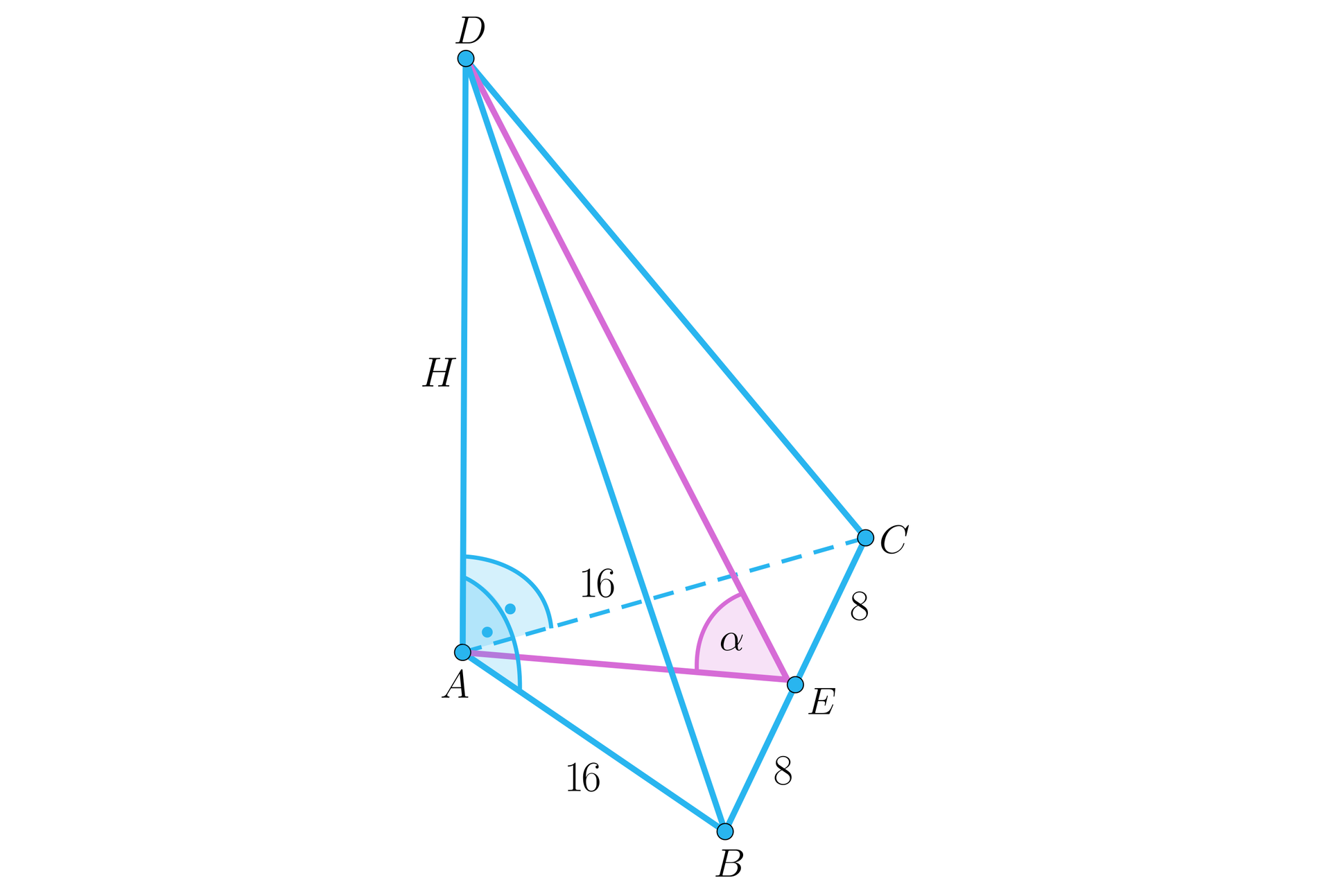
Ilustracja przedstawia ostrosłup, którego podstawą jest trójkąt A B C, wierzchołek górny podpisano literą D. Kąt BAD oraz kąt CAD są kątami prostymi. Odcinek AD podpisano literą H. A wierzchołka D na krawędź BC opuszczono wysokość , jej spodek podpisano literą C. W podstawie zaznaczono odcinek AE. Kąt AED podpisano literą alfa. Odcinki AC oraz AC mają długość 16, z kolei odcinki BE oraz CE mają długość osiem.

Oznaczymy długość wysokości ostrosłupa przez $H$ oraz kąt $α = 60 °$ .

W trójkącie równobocznym $A B C$ , odcinek $A E$ jest jego wysokością, więc

$|A E| = \frac{16 \sqrt{3}}{2} = 8 \sqrt{3}$ .

Obliczamy pole podstawy:

$P_{p} = \frac{1}{2} \cdot |B C| \cdot |A E| = \frac{1}{2} \cdot 16 \cdot 8 \sqrt{3} = 64 \sqrt{3}$

W celu obliczenia powierzchni ścian bocznych wyznaczymy długość wysokości $H$ oraz długość odcinka $E D$ , który jest wysokością trójkąta $B C D$ .

Z trójkąta $A E D$ , który jest prostokątny mamy:

$tg α = \frac{H}{|A E|}$

$tg 60 ° = \frac{H}{8 \sqrt{3}}$

$\sqrt{3} = \frac{H}{8 \sqrt{3}}$

$H = 24$

oraz

$\cos α = \frac{|A E|}{|E D|}$

$\cos 60 ° = \frac{8 \sqrt{3}}{|E D|}$

$\frac{1}{2} = \frac{8 \sqrt{3}}{|E D|}$

$|E D| = 16 \sqrt{3}$

Obliczamy pola ścian bocznych:

$P_{A B D} = P_{A C D} = \frac{1}{2} \cdot |A B| \cdot H = \frac{1}{2} \cdot 16 \cdot 24 = 192$

oraz

$P_{B C D} = \frac{1}{2} \cdot |B C| \cdot |E D| = \frac{1}{2} \cdot 16 \cdot 16 \sqrt{3} = 128 \sqrt{3}$

Obliczamy pole powierzchni całkowitej ostrosłupa:

$P = P_{p} + P_{b} = 64 \sqrt{3} + 2 \cdot 192 + 128 \sqrt{3} = 384 + 192 \sqrt{3}$

Odpowiedź: $P = 384 + 192 \sqrt{3}$

Przykład 3

W ostrosłupie prawidłowymostrosłup prawidłowyostrosłupie prawidłowym trójkątnymostrosłup prawidłowy trójkątnytrójkątnym ściany boczne są nachylone do podstawy pod kątem $α$ . Wysokość ostrosłupa jest równa $H$ . Oblicz pole powierzchni całkowitej ostrosłupa.

Rozwiązanie:

Wykonujemy rysunek z odpowiednimi oznaczeniami.

R11UxBF3Sz6qL

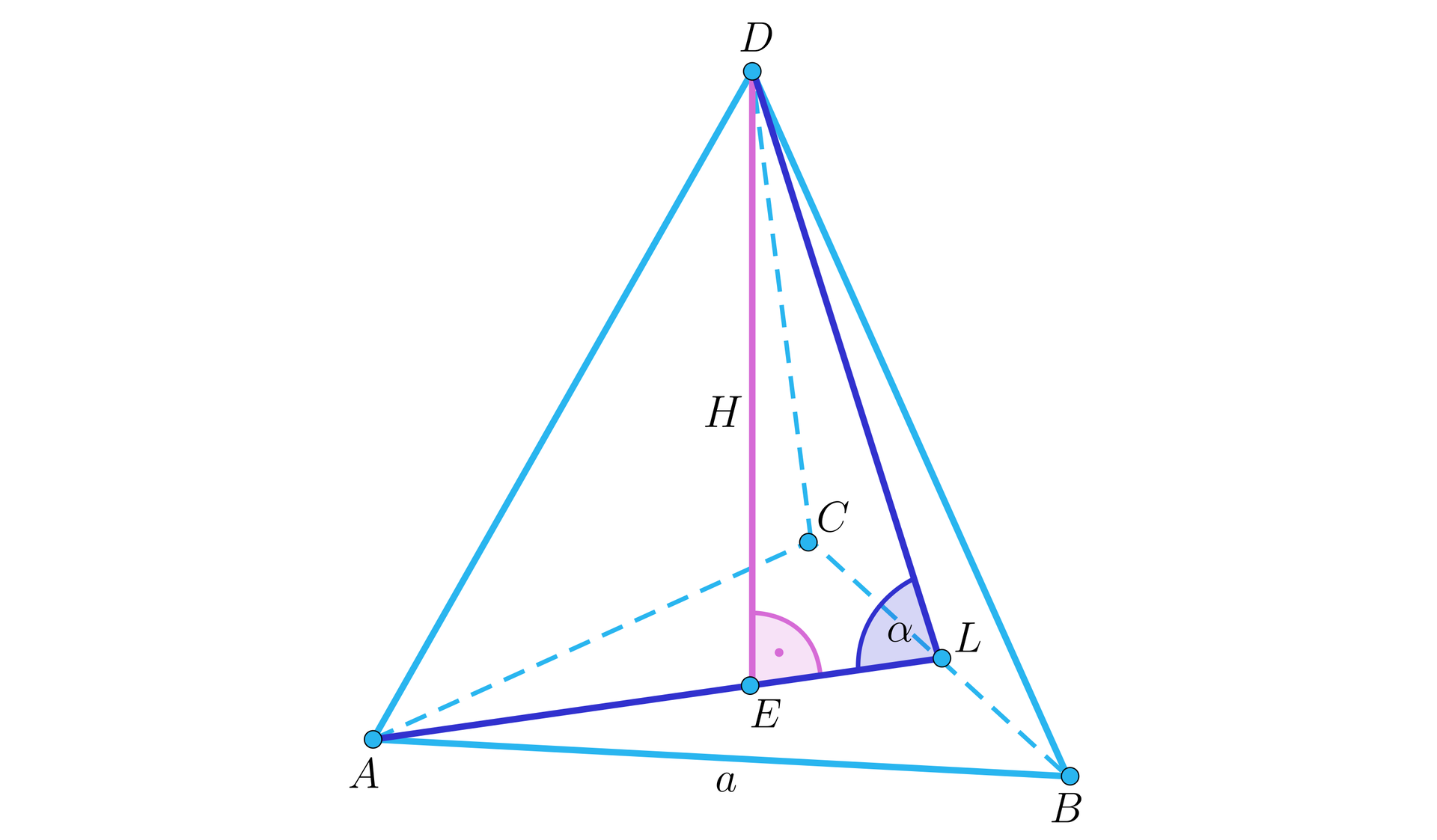
Ilustracja przedstawia ostrosłup, którego podstawą jest trójkąt A B C, wierzchołek górny podpisano literą D. Wysokość ostrosłupa podpisano literą H, a jej spodek podpisano literą E. Na krawędzi BC znajduje się punkt L, kąt ALD podpisano literą alfa. Krawędź AB podpisano literą a.

Wiemy, że w podstawie ostrosłupa prawidłowegoostrosłup prawidłowyostrosłupa prawidłowego jest trójkąt równoboczny, więc odcinek $E L$ ma długość:

$|E L| = \frac{1}{3} \cdot \frac{a \sqrt{3}}{2} = \frac{a \sqrt{3}}{6}$ .

Z trójkąta $E L D$ mamy:

$tg α = \frac{H}{|E L|} = \frac{H}{\frac{a \sqrt{3}}{6}}$ , $\frac{a \sqrt{3}}{6} = H \cdot ctg α$ , więc $a = 2 \sqrt{3} \cdot H \cdot ctg α$

Obliczamy pole podstawy ostrosłupa:

$P_{p} = \frac{a^{2} \sqrt{3}}{4} = \frac{4 \cdot 3 \sqrt{3} \cdot H^{2} \cdot {ctg}^{2} α}{4} = 3 \sqrt{3} \cdot H^{2} \cdot {ctg}^{2} α$

W celu obliczenia powierzchni ścian bocznych wyznaczymy długość wysokości $D L$ , który jest wysokością trójkąta $B C D$ .

Z trójkąta $E L D$ mamy:

$\sin α = \frac{H}{|D L|}$ , stąd $|D L| = \frac{H}{\sin α}$

Mamy już pole podstawy, obliczymy pole powierzchni bocznej, która jest sumą pól ścian bocznych ostrosłupa. W tym celu obliczymy pole trójkąta $B C D$ .

$P_{B C D} = \frac{1}{2} \cdot |B C| \cdot |D L| = \frac{1}{2} \cdot a \cdot \frac{H}{\sin α} = \frac{1}{2} \cdot 2 \sqrt{3} \cdot H \cdot ctg α \cdot \frac{H}{\sin α} = \frac{H^{2} \sqrt{3} \cdot ctg α}{\sin α}$

$P_{b} = 3 \cdot \frac{H^{2} \sqrt{3} \cdot ctg α}{\sin α} = \frac{3 \sqrt{3} \cdot H^{2} \cdot ctg α}{\sin α}$

Zatem pole powierzchni ostrosłupa:

$P = P_{p} + P_{b} = 3 \sqrt{3} \cdot H^{2} \cdot {ctg}^{2} α + \frac{3 \sqrt{3} \cdot H^{2} \cdot ctg α}{\sin α} = 3 \sqrt{3} \cdot H^{2} (\frac{\cos^{2} α + \cos α}{\sin^{2} α})$

Słownik

ostrosłup prawidłowy

ostrosłup, którego podstawą jest wielokąt foremny i spodek wysokości ostrosłupa pokrywa się ze środkiem okręgu opisanego na jego podstawie

spodek wysokości bryły

rzut prostokątny wierzchołka bryły na płaszczyznę podstawy

ostrosłup prawidłowy trójkątny

ostrosłup prawidłowy, którego podstawą jest trójkąt równoboczny

czworościan foremny

ostrosłup prawidłowy trójkątny, którego wszystkie cztery ściany są trójkątami równobocznymi

Wprowadzenie

Animacja 3D

Słownik