Przeczytaj

Pojęcie łamanej i jej rodzaje

łamana

Definicja: łamana

Łamaną nazywamy figurę geometryczną, którą można przedstawić jako sumę skończonej liczby odcinków, w taki sposób, że:

dowolne dwa odcinki mogą mieć co najwyżej wspólny koniec (co najwyżej jeden punkt wspólny),
odcinki można tak uporządkować (ponumerować), aby koniec jednego odcinka (oprócz ewentualnie ostatniego) był początkiem następnego.

Wtedy odcinki tworzące łamaną nazywamy bokami tej łamanej, a końce tych odcinków nazywamy wierzchołkami łamanej.

RhnkyPJo4cxkV

Ilustracja przedstawia 4 łamane. Pierwsza posiada 3 boki. Jest ona podobna do trójkąta, którego dwa ramiona zostały przedłużone. Druga łamana przypomina niezaokrągloną spiralę składającą się z 12 boków. Trzecia łamana jest to koperta posiadająca 8 boków . Figura ta zbudowana jest z prostokąta leżącego na dłuższym boku wraz z jego dwoma przekątnymi. Na górnej podstawie prostokąta znajduje się trójkąt równoramienny. Ostatnia łamana zbudowana jest z 9 boków. Kształtem przypomina grotę strzały zbudowaną z 6 boków dodatkowo obudowaną z prawej strony czterema bokami. — przykłady łamanej

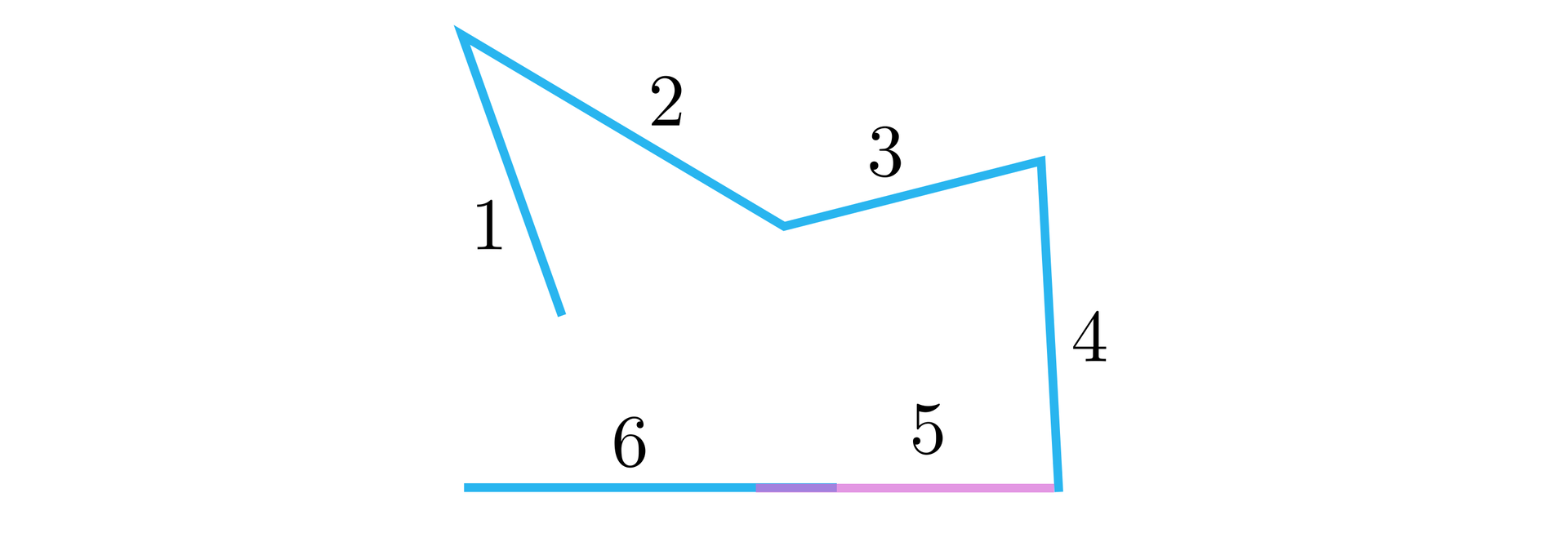
Zauważmy, że gdyby pierwszą z figur potraktować jako sumę mnogościową tylko trzech odcinków, to ta figura nie spełniałaby warunków opisanych w definicji łamanej. Musimy więc dostrzec podział dwóch spośród tych odcinków i mówić o łamanej składającej się z pięciu boków.

Zauważmy, że nie każdą figurę zbudowaną ze skończonej liczby odcinków nazwiemy łamaną. W szczególności, jeśli jakieś dwa kolejne odcinki w naszej figurze będą współliniowe i będą miały więcej niż jeden punkt wspólny, to taka figura nie będzie łamaną. Na rysunku poniżej odcinki o numerach 5 i 6 mają więcej niż jeden punkt wspólny.

R1YDDS6qntzkf

Ilustracja przedstawia figurę składającą się z sześciu boków. Rozpoczyna się ona czteroma odcinkami tworzącymi kształt rogów. Odcinek piąty i szósty są do siebie równoległe i zaczynają się w tym samym punkcie, pokrywają się. — Przykład figury, która jest skończona sumą uporządkowanych odcinków, ale nie jest łamaną

Zauważmy, że każdą łamaną, w szczególności ze względu na wymóg uporządkowania odcinków, da się narysować „bez odrywania” ołówka od kartki, czyli łamana jest figurą unikursalnąfigura unikursalnafigurą unikursalną. Tym samym, te figury, które są zbudowane ze skończonej liczby odcinków, ale których nie da się narysować „bez odrywania” ołówka od kartki, nie będą łamaną.

RHO3GQ2wnUu1G

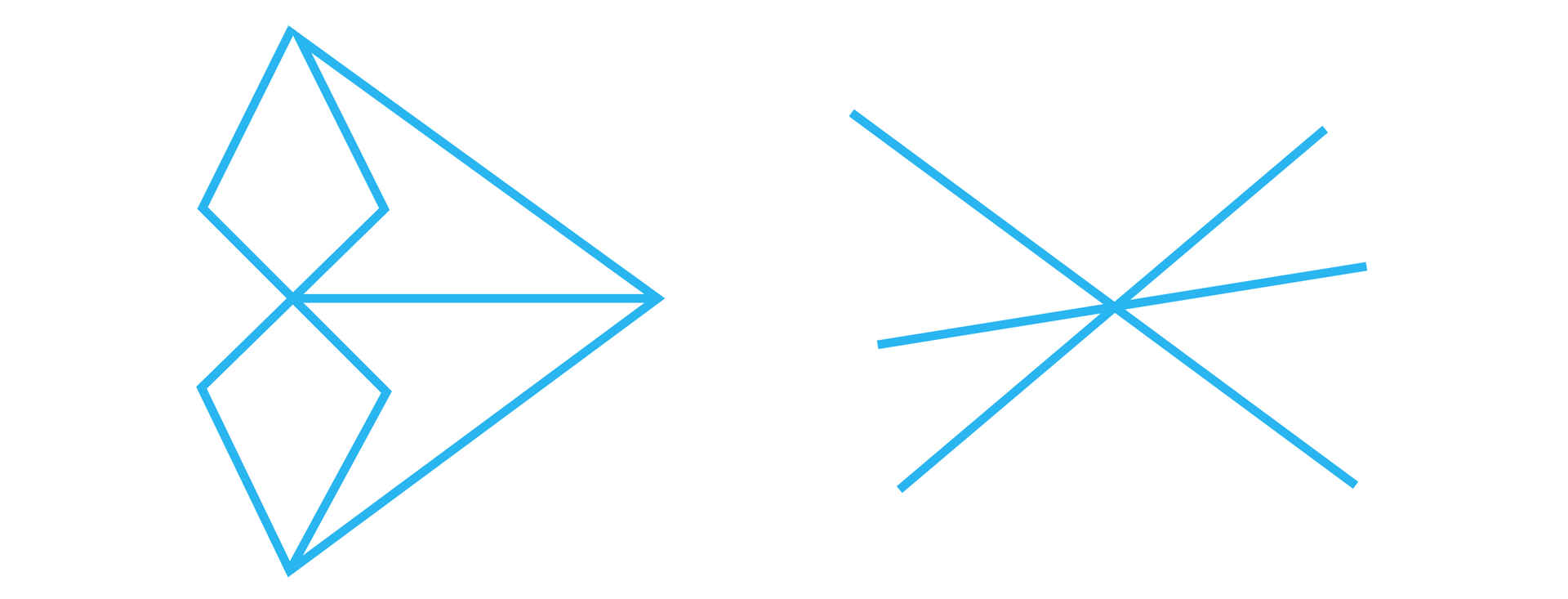
Ilustracja prezentuje dwie figury nie będącymi łamanymi. Pierwsza z nich składa się z dwóch deltoidów symetrycznych względem górnego wierzchołka dolnej figury. Z punktu symetrii obu deltoidów poprowadzony został w prawo poziomy odcinek, z którego końca poprowadzono dwa odcinki łączące wierzchołki symetrycznych deltoidów, które znajdują się na przeciwko wierzchołków znajdujących się w puncie symetrii. Druga figura zbudowana jest natomiast z trzech przecinających się w jednym punkcie prostych. — przykłady figur, które są skończoną sumą odcinków, ale nie są łamaną

łamana zwyczajna

Definicja: łamana zwyczajna

Łamana, której dwa kolejne odcinki nie leżą na jednej prostej oraz żaden punkt tej łamanej nie należy do więcej niż dwóch odcinków, nazywa się łamaną zwyczajną.

łamana zamknięta

Definicja: łamana zamknięta

Łamana zwyczajna jest zamknięta, jeśli koniec ostatniego odcinka pokrywa się z początkiem pierwszego odcinka. W przeciwnym razie łamaną nazywa się otwartą.

R1IwsZlXKBETz

Ilustracja przedstawia łamaną zwyczajną zamkniętą przypominającą kształtem grot strzały. Figura ta posiada cztery boki. — łamana zwyczajna zamknięta

R1Qf5ksM2iUJ2

Ilustracja przedstawia łamaną zwyczajną otwartą, przypominającą kształtem grot strzały. Figura ta posiada jednak tylko trzy boki przez co nie jest ona domknięta. — łamana zwyczajna otwarta

łamana wiązana

Definicja: łamana wiązana

Łamaną nazywamy wiązaną, jeśli istnieje takie uporządkowanie (taki podział na sumę odcinków), przy którym ta łamana ma punkt należący do więcej niż dwóch odcinków.

RSpbEZQwrD9Ty

Ilustracja przedstawia dwie łamane wiązane. Pierwsza z nich składa się z czterech boków i zbudowana jest z trójkąta ostrokątnego i jednej pionowej półprostej ograniczonej wierzchołkiem trójkąta. Druga łamana jest zbudowana z 7 boków i przypomina kształtem gwiazdę. — przykłady łamanych wiązanych

Drugi z powyższych wielokątów jest przykładem wielokąta gwiaździstegowielokąt foremny gwiaździstywielokąta gwiaździstego - jest to jeden spośród dwóch siedmiokątów gwiaździstych.

wielokąt

Definicja: wielokąt

Wielokątem (inaczej wielobokiem, $n$ -kątem, $n$ -bokiem) nazywamy płaska figurę geometryczną ograniczoną łamaną zwyczajną zamkniętą o $n$ bokach, gdzie $n ⩾ 3$ , wraz z tą łamaną.

wielokąt wypukły

Definicja: wielokąt wypukły

Wielokątem, który jest figurą wypukłą nazywamy wielokątem wypukłym.

o wielokącie wypukłym

Twierdzenie: o wielokącie wypukłym

Wielokąt jest wypukły wtedy i tylko wtedy, gdy spełniony jest jeden z poniższych warunków:

każde dwa punkty wielokąta można połączyć odcinkiem zawartym w tym wielokącie;
wszystkie kąty wewnętrzne wielokąta są wypukłe;
wielokąt zawiera wszystkie swoje przekątne.

Zagadnienie izoperymetryczne

Dla każdego wielokąta możemy obliczyć jego obwód, który jest sumą długości boków łamanej, która jest brzegiem danego wielokąta. Podobnie możemy obliczać pole każdego wielokąta, np. sprowadzając to zagadnienie do obliczenia sumy pól rozłącznych trójkątów, na które można podzielić każdy wielokąt (tzw. triangulacja). Rozważmy dwunastokąt foremny o obwodzie równym $1$ , taki jak na rysunku, którego triangulacja (podział na rozłączne trójkąty) została wyznaczona przez promienie okręgu opisanego na tym wielokącie.

RRBUuEndWEP1U

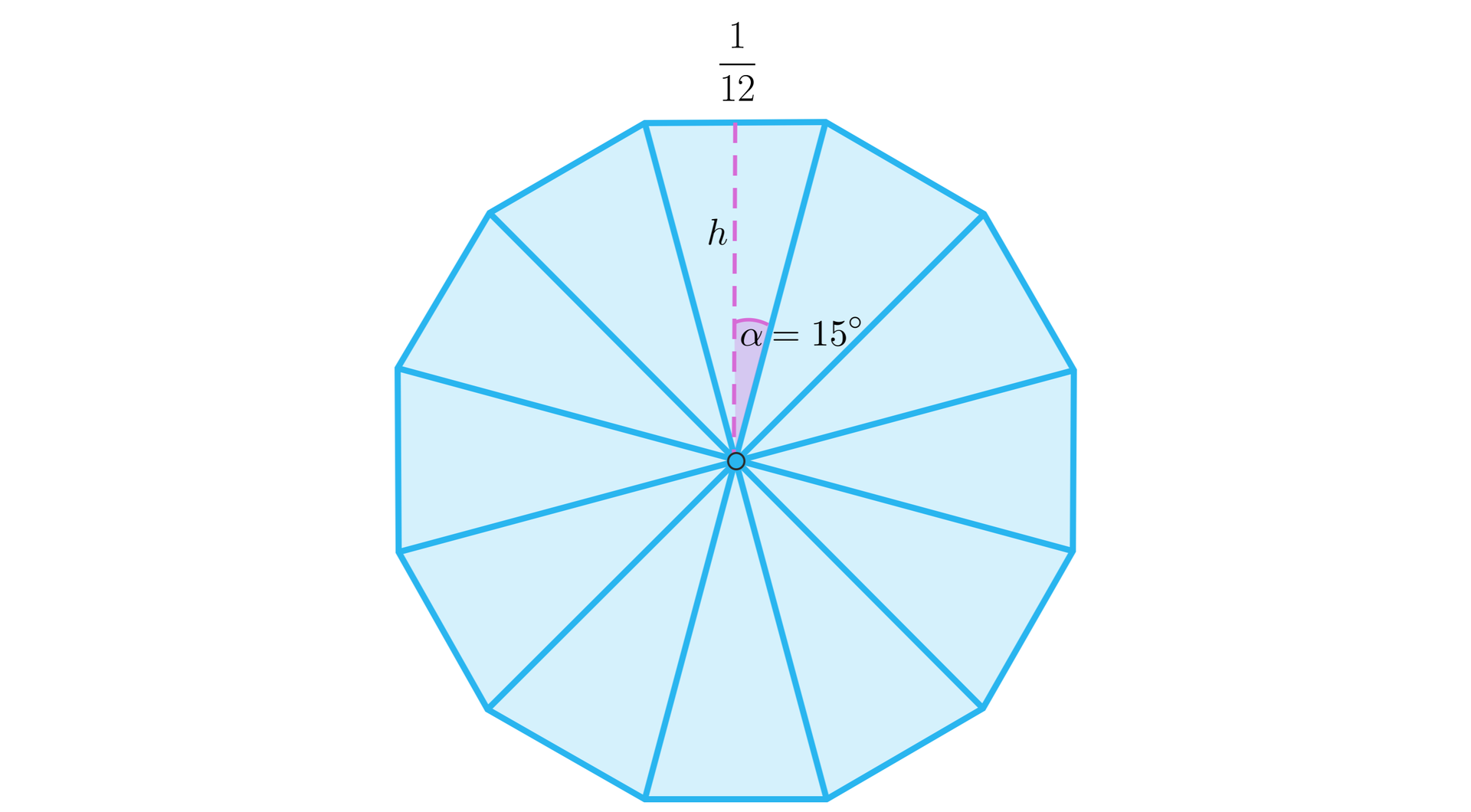
Ilustracja prezentuję dwunastokąt foremny o obwodzie równym 1. Figura ta została podzielona na dwanaście równych trójkątów równoramiennych, w jednym z nich na podstawę ze środka figury upuszczona została wysokość h. Zaznaczony został także kąt alfa wynoszący 15 stopni. Znajduje się on pomiędzy wysokością trójkąta równoramiennego, a jego ścianą boczną.

Zauważmy, że $tg 15 ° = \frac{\frac{1}{2} \cdot \frac{1}{12}}{h}$ . Wtedy $h = \frac{\frac{1}{24}}{tg 15 °}$ i pole dwunastokąta jest równe $p = 12 (\frac{1}{2} \cdot \frac{1}{12} \cdot h) = 12 (\frac{1}{2} \cdot \frac{1}{12} \cdot \frac{\frac{1}{24}}{tg 15 °}) = \frac{1}{48 \cdot tg 15 °} = \frac{1}{48 \cdot (2 - \sqrt{3})} = \frac{\sqrt{3} + 2}{48} \approx 0, 077751$ . Przechodząc do zagadnień izoperymetrycznych, zacznijmy od tego, że termin „izoperymetria” ma swój źródłosłów w przedrostku „izos” – równy, taki sam oraz „perimetros” – obwód. Klasyczne zagadnienie izoperymetryczne, przywołane m.in. przez Zenodora na przełomie III i II wieku p.n.e. głosi, że wśród wielokątów o ustalonym obwodzie i o jednakowej liczbie boków wielokąt foremnywielokąt foremnywielokąt foremny ma największe pole. Z kolei podstawowe twierdzenie izoperymetryczne głosi, że wśród wszystkich krzywych na płaszczyźnie o ustalonym obwodzie, figurę o największym polu ogranicza okrąg. Jako ciekawostkę warto wspomnieć, że ten aspekt przywołany został przez Adama Mickiewicza w IV księdze „Panu Tadeusza”, gdy wspomina o fortelu zastosowanym przez Dydonę – ta miała obiecane, że dostanie tyle ziemi, ile obejmie skóra wołu. Pocięła więc skórę na wąskie paski i utworzyła z nich okrąg, a na terenie w ten sposób wydzielonym miała powstać Byrsa – najstarsza dzielnica Kartaginy.

Okazuje się, że dla dowolnych figur o polu $P$ i obwodzie $L$ prawdziwa jest nierówność $\frac{4 π \cdot P}{L^{2}} \leq 1$ , a iloraz $Q = \frac{4 π \cdot P}{L^{2}}$ zwany jest ilorazem izoperymetrycznym.

Zbadajmy iloraz izoperymetrycznyiloraz izoperymetrycznyiloraz izoperymetryczny dla koła. Mamy: $\frac{4 π \cdot P}{L^{2}} = \frac{4 π \cdot (π r^{2})}{{(2 π r)}^{2}} = 1$ . Okazuje się, że jest to jedyna figura, dla której ten iloraz jest jedynką. Twierdzenie Zenodora można sformułować wykorzystując zdefiniowany wyżej iloraz.

o ilorazie izoperymetrycznym

Twierdzenie: o ilorazie izoperymetrycznym

Spośród wszystkich wielokątów o danym obwodzie największy iloraz izoperymetryczny ma wielokąt foremny.

Przywołane wyżej twierdzenia przyjmiemy bez dowodu. Przyjrzymy się jednak zagadnieniom, które z tymi zależnościami są związane.

problem odwrotny izoperymetrii dla trójkąta

Twierdzenie: problem odwrotny izoperymetrii dla trójkąta

Ze wszystkich trójkątów o ustalonej podstawie i równych polach trójkąt równoramienny ma najmniejszy obwód.

Dowód

Rozważmy dowolny trójkąt $A B C$ o różnych bokach. Poprowadźmy prostą równoległą do podstawy $A B$ , przechodząca przez punkt $C$ . Niech $D$ będzie punktem wspólnym tej prostej i symetralnej odcinka $A B$ , jak na rysunku.

RTX2kmPamwnS6

Ilustracja przedstawia dwa trójkąty A B C oraz A B D leżące na tej samej podstawie A B. Punkty C i D są położone na przerywanej prostej równoległej do odcinka A B. Punkt B został odbity względem przerywanej prostej tworząc trójkąt C D B prim. Odcinek A D, B D oraz D B prim mają taką samą długość i są zamalowane granatowym kolorem. Odcinek A B i A C także mają taką samą długość i są w kolorze niebieskim, natomiast odcinki B C i C B prim są w kolorze różowym i również są tej samej długości.

Wtedy trójkąt $A B D$ jest równoramienny i pola trójkątów $A B C$ i $A B D$ są równe. Niech $B'$ będzie obrazem punktu $B$ w symetrii względem prostej $C D$ .

Wtedy $|B C| = |C B'|$ , $|B D| = |D B'|$ oraz punkty $A$ , $D$ , $B'$ są współliniowe i $|A D| = |D B'|$ . Rozważmy obwód trójkąta $A B C$ : $|A B| + |B C| + |A C|$ . Mamy wówczas $|A B| + |B C| + |A C| = |A B| + |C B'| + |A C|$ . Z nierówności trójkąta wynika, że $|A C| + |C B'| \geq |A B'|$ , ale $|A B'| = |A D| + |D B'|$ . Zatem: $|A B| + |B C| + |A C| \geq |A B| + |B D| + |A D|$ . Ale ostatnia suma opisuje obwód trójkąta równoramiennego $A B D$ . Stąd teza.

Słownik

figura unikursalna

figura, którą można nakreślić jednym pociągnięciem ołówka (bez jego odrywania od kartki), nie prowadząc go nigdy po linii już nakreślonej

iloraz izoperymetryczny

ilorazem izoperymetrycznym figury płaskiej o polu $P$ i obwodzie $L$ nazywamy liczbę $\frac{4 π \cdot P}{L^{2}}$

wielokąt foremny gwiaździsty

$n$ -kątem foremnym gwiaździstym nazywamy łamaną zamkniętą o $n$ wierzchołkach, utworzoną z tych przekątnych $n$ -kąta foremnego, które mają równą długość

wielokąt foremny

wielokątem foremnym nazywamy taki wielokąt, którego wszystkie boki mają taką samą długość i kąty wewnętrzne są przystające (mają równe miary)

Wprowadzenie

Prezentacja multimedialna

Pojęcie łamanej i jej rodzaje

Zagadnienie izoperymetryczne

Słownik