Modelowanie ruchów Browna

Pierwsze matematyczne modele ruchów Browna podali niezależnie od siebie Albert Einstein i polski fizyk, Marian Smoluchowski. Obydwaj naukowcy stwierdzili, że pyłek kwiatowy przemieszcza się z miejsca na miejsce, ponieważ jest nieustannie bombardowany przez cząsteczki wody; cały proces ma charakter przypadkowy.

W tym e‑materiale przedstawimy ruchy Browna w postaci graficznej, jako linię złożoną z odcinków łączących punkty w kartezjańskim układzie współrzędnych. Każdy punkt będzie odpowiadał położeniu cząsteczki na kolejnym etapie symulacji.

Kartezjański układ współrzędnych to dwie prostopadłe do siebie osie X oraz Y. Punkt ich przecięcia oznaczamy jako (0,0) – jest to środek (tzw. zero) układu współrzędnych.

RwTvdVetSmrx9

Ilustracja

Wstępnie przyjmiemy kilka założeń:

• umieścimy cząsteczkę na początku układu współrzędnych (0,0),

• kierunek ruchu będzie wyznaczony przez losowy kąt φphi,

• cząsteczka będzie przemieszczała się skokami na odległość r, zależną od kąta φphi,

• kolejne współrzędne cząsteczki (x,y) wyliczymy ze wzorów:

W rezultacie otrzymamy tablice (listy) współrzędnych XIndeks dolny nn oraz YIndeks dolny nn. Pary te wskazują położenie cząsteczki po każdym skoku w przypadkowym kierunku.

Eksperyment

W celu zaobserwowania ruchów Browna, możemy przeprowadzić prosty eksperyment. Do szklanki z wodą wlewamy kilka kropli syropu. Zauważyć możemy wówczas samoistne mieszanie się płynów. Zjawisko to nazywane jest dyfuzją i spowodowane jest w dużej mierze ruchami Browna.

Kolejny eksperyment, który można wykonać w domu, polega na umieszczeniu kropli oleju w misce z wodą. Zaobserwować możemy, że kropla oleju nie pozostaje bez ruchu. Po kilku minutach cząsteczka przemieści się w inne miejsce. Po następnych kilku minutach w jeszcze inne itd. Przemieszczanie to można wytłumaczyć występowaniem ruchów Browna.

Modelowanie ruchów Browna

Model programistyczny, który przyjmiemy, będzie polegał na utworzeniu cząsteczki oraz umieszczeniu jej w płynie. W procesie losowego bombardowania cząsteczki przez cząsteczki płynu będzie przemieszczała się ona o określoną odległość. Wynikiem działania programu będzie wskazanie końcowego położenia cząsteczki.

Cząsteczkę, którą będziemy modelować, możemy opisać dwoma zmiennymi  oznaczającymi jej współrzędne w układzie kartezjańskim. Jako jej początkowe położenie przyjmiemy punkt (0, 0).

// utworzenie cząsteczki
x = 0.0
y = 0.0

Kolejnym etapem będzie symulowanie bombardowania cząsteczki przez losową cząsteczkę płynu. W tym celu musimy wygenerować losowy kąt $\phi$, w którym przemieści się cząsteczka.

Ponieważ ruchy Browna są losowe, możemy założyć, że będziemy modelować uśrednioną wersję. Przyjmijmy zatem, że każda cząsteczka płynu uderza naszą cząstkę z taką samą siłą, w wyniku czego nasza cząsteczka przesuwa się zawsze o taką samą odległość.

W większości języków programowania wbudowane są funkcje matematyczne takie jak sinus oraz cosinus. Przyjmują one argumenty wyrażone w radianachradianradianach. Aby wyznaczyć losowy kąt $\phi$, generujemy liczbę pseudolosową z przedziału $\left\langle0,\ 2\pi\right)$. Języki programowania udostępniają generator liczb pseudolosowych w różny sposób, jednak my założymy, że dysponujemy funkcją random(), która generuje liczbę losową z przedziału $\left\langle0,\ 1\right)$. W celu przeskalowania tego przedziału na interesujący nas przedział wystarczy pomnożyć wylosowaną liczbę przez $2\pi$. Ponieważ w językach programowania dostępne są również stałe matematyczne, załóżmy, że dysponujemy stałą PI, która równa jest przybliżeniu liczby $\pi$.

// losowy kąt fi
fi = random() * 2 * PI;

Jak wspomnieliśmy wcześniej, nie musimy zastanawiać się nad implementacją funkcji trygonometrycznych. Zakładamy, że dostępne są funkcje sinus() oraz cosinus(). Reprezentacją wektora będą dwie zmienne. Aby przesunąć cząsteczkę o wyznaczony wektor, dodajmy jego współrzędne odpowiednio do współrzędnych cząsteczki. Nazwijmy zatem te zmienne dx oraz dy.

Kolejne współrzędne (x, y) cząstki będą określone następującymi wzorami:

// wektor kierunku ruchu o wartości r ustawiony pod kątem fi
dx = r * cosinus(fi)
dy = r * sinus(fi)

Na poniższej grafice widzimy wykorzystane powyżej własności:

R1GAjeGEajrzm

Ilustracja

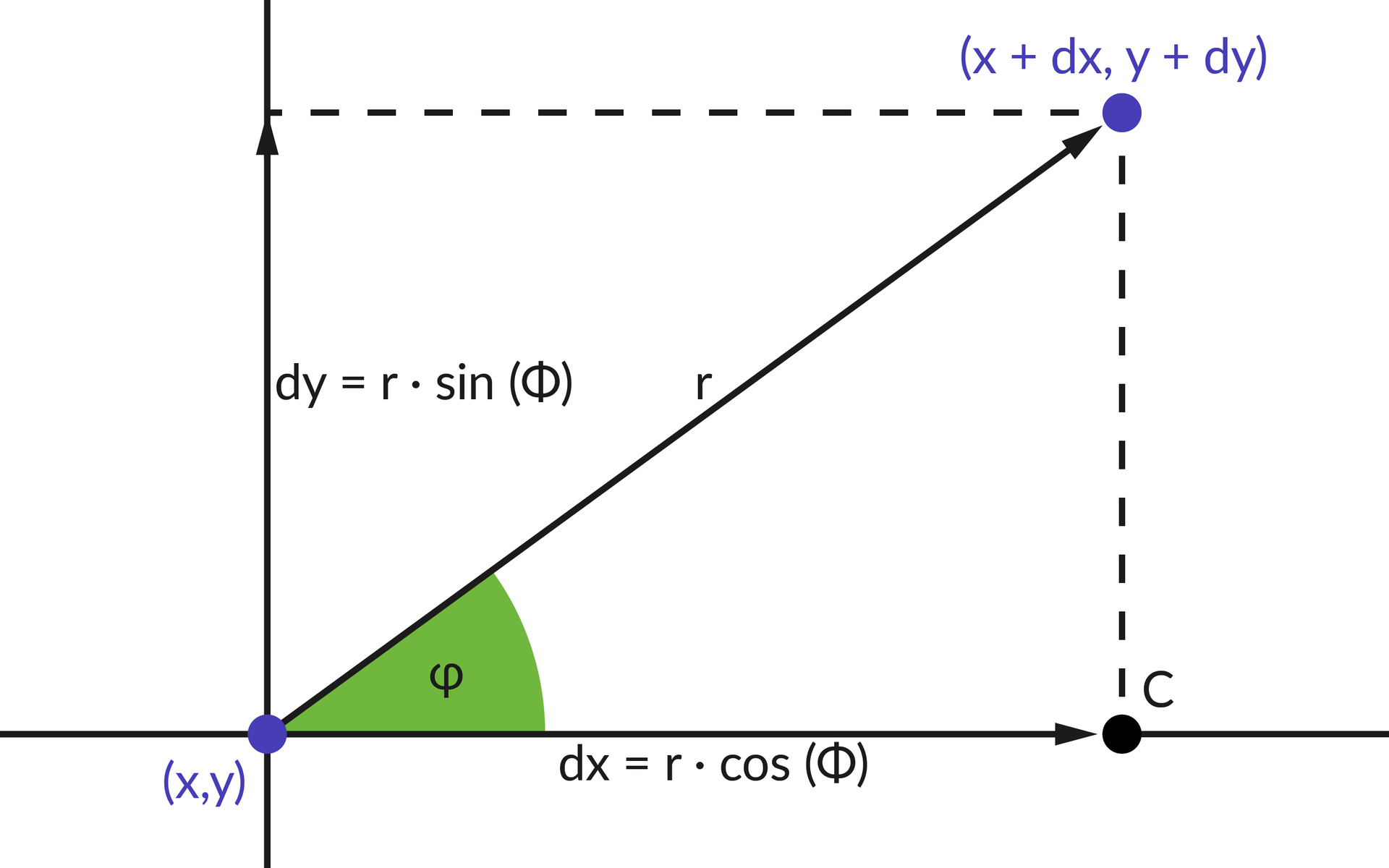
Przeprowadzając modelowanie ruchów Browna, zależy nam na procesie, w którym zachodzi więcej niż tylko jedna kolizja. Aby zwiększyć ich liczbę, możemy utworzyć pętlę, która będzie symulowała n kolizji następujących po sobie. W pętli możemy również wypełniać dwie tablice, które będą przechowywały współrzędne punktów, w których znajdowała się cząsteczka. Jedna tablica jest potrzebna do przechowywania współrzędnych osi x, druga – y.

Przykładowy program modelujący ruchy Browna może być napisany zgodnie z poniższym pseudokodem.

// liczba kolizji
n = 100

// długość wektora
r = 0.1

// początkowe położenie cząsteczki
x = 0.0
y = 0.0

// tablice przechowujące kolejne pozycje cząsteczki
deklaracja tablicy ruchyX o wielkości n + 1
deklaracja tablicy ruchyY o wielkości n + 1

// zapisz w tablicach początkowe położenie cząsteczki
ruchyX[0] = x
ruchyY[0] = y

dla i = 1, 2, ..., n wykonuj
	// losowy kąt fi
	fi = random() * 2 * PI;

	dx = r * cosinus(fi)
    dy = r * sinus(fi)
    
    x = x + dx
    y = y + dy
    
    // zapisz w tablicach obecne położenie cząsteczki
	ruchyX[i] = x
	ruchyY[i] = y

// wypisz końcową pozycję
wypisz x
wypisz y

Słownik