Przeczytaj

Funkcję określoną wzorem

f (x) = a x^{2} + b x + c

x \in ℝ

gdzie $a$ , $b$ , $c$ są liczbami rzeczywistymi, przy czym $a \neq 0$ , nazywamy funkcją kwadratową. Gdy wyróżnik trójmianu kwadratowego

∆ = b^{2} - 4 a c

jest nieujemny, to funkcja ma miejsca zerowe:

x_{1} = \frac{- b + \sqrt{∆}}{2 a}

x_{2} = \frac{- b - \sqrt{∆}}{2 a}

Pokażemy teraz przykładowe zadania tekstowe, w których interpretując zagadnienie geometryczne, wykorzystamy własności funkcji kwadratowejfunkcja kwadratowafunkcji kwadratowej.

Przykład 1

Obwód rombu jest równy $60 cm$ , a różnica długości jego przekątnych $6 cm$ . Oblicz długości przekątnych tego rombu.

W rombie:

przekątne dzielą się na połowy i są wzajemnie prostopadłe,
przekątne są dwusiecznymi kątów.

R196PPIqDuQyj

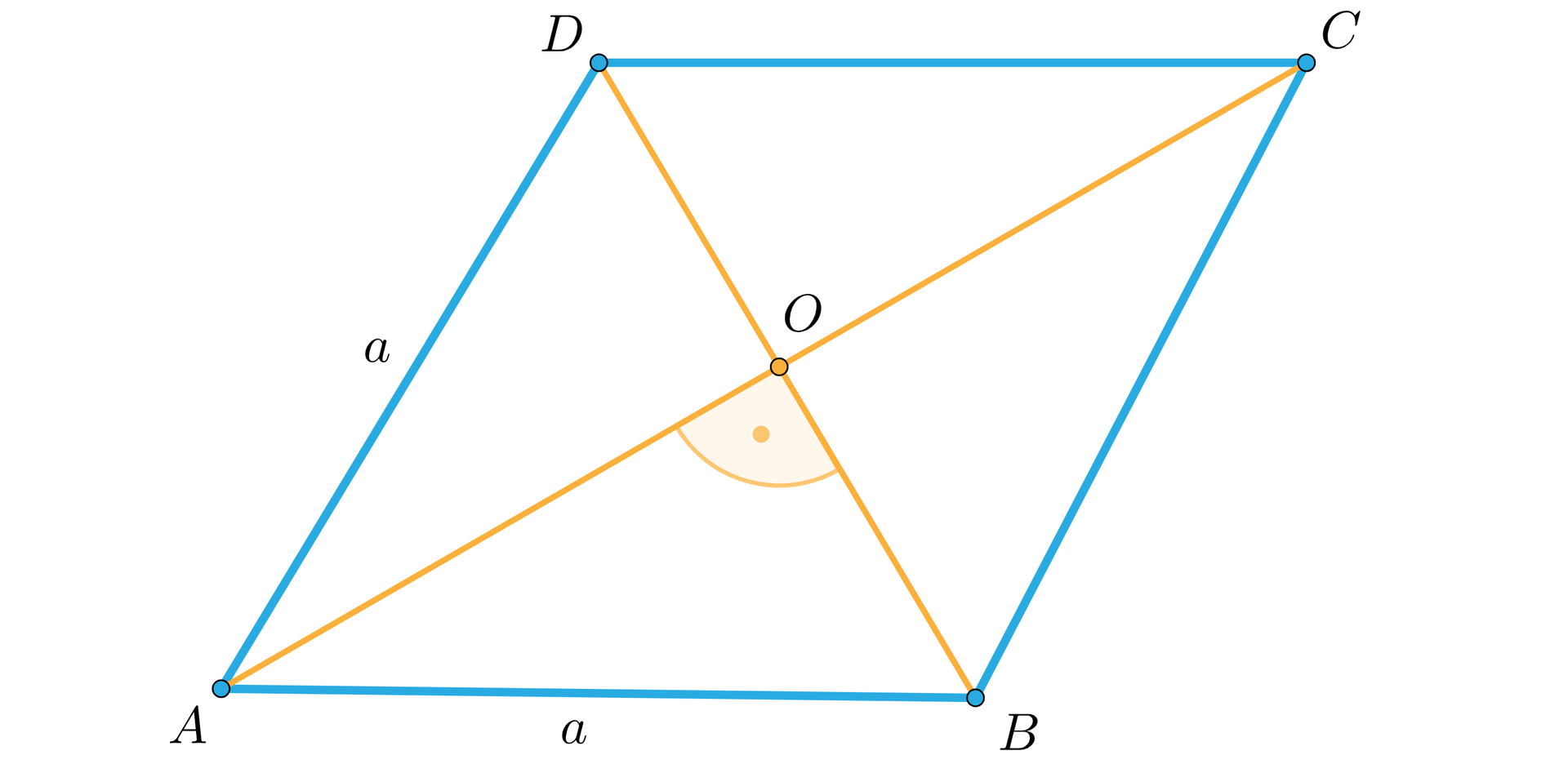
Ilustracja przedstawia romb A B C D z zaznaczonymi przekątnymi A C i B D przecinającymi się w punkcie O. Boki rombu mają długość a.

Rozwiązanie:

Z rysunku mamy poniższe zależności:

$|A B| = |B C| = |C D| = |D A| = a$

$|A C| - |D B| = 6$

$|D B| = |A C| - 6$

$|A C| = x$

$| D B | = x - 6$ , $x > 6$ ,

gdzie $|A C|$ to dłuższa przekątna rombu, natomiast $|D B|$ to krótsza przekątna rombu.

Trójkąt $A O B$ jest trójkątem prostokątnym. Zapiszmy zatem długości przyprostokątnych tego trójkąta.

$|A O| = \frac{1}{2} x$

$|B O| = \frac{1}{2} (x - 6)$

Wzór na obwód rombu: $L = 4 a$ i $L = 60 cm$ .

$4 a = 60$

$a = 15 \Rightarrow x > 15$

Z twierdzenia Pitagorasa dla trójkąta $A O B$ :

${(\frac{1}{2} x)}^{2} + {[\frac{1}{2} (x - 6)]}^{2} = 15^{2}$

$\frac{1}{4} x^{2} + \frac{1}{4} {(x - 6)}^{2} = 225$ .

Mnożymy stronami przez $4$ i korzystamy ze wzoru skróconego mnożenia na kwadrat różnicy: ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ .

$x^{2} + {(x - 6)}^{2} = 900$

$x^{2} + x^{2} - 12 x + 36 = 900$

$2 x^{2} - 12 x - 864 = 0$

$∆ = b^{2} - 4 a c = 144 - 4 \cdot 2 \cdot (- 864) = 144 + 6912 = 7056$

$\sqrt{∆} = \sqrt{7056} = 84$

$x_{1} = \frac{- b + \sqrt{∆}}{2 a} = \frac{- (- 12) + \sqrt{7056}}{2 \cdot 2} = \frac{12 + 84}{4} = \frac{96}{4} = 24$

$x_{2} = \frac{- b - \sqrt{∆}}{2 a} = \frac{- (- 12) - \sqrt{7056}}{2 \cdot 2} = \frac{12 - 84}{4} = \frac{- 72}{4} = - 18 < 0$

Długość przekątnej nie może być ujemna, zatem z powyższych obliczeń mamy, że $x = 24$ , a więc $|A C| = 24$ oraz $|D B| = x - 6 = 24 - 6 = 18$ .

Odp.: Dłuższa przekątna ma długość $24 cm$ , a krótsza $18 cm$ .

Przykład 2

W trójkącie prostokątnym stosunek długości przyprostokątnych wynosi $4 : 3$ . Znaleźć długości przyprostokątnych, jeżeli przeciwprostokątna ma długość $20 cm$ .

R1OripqafcQAd

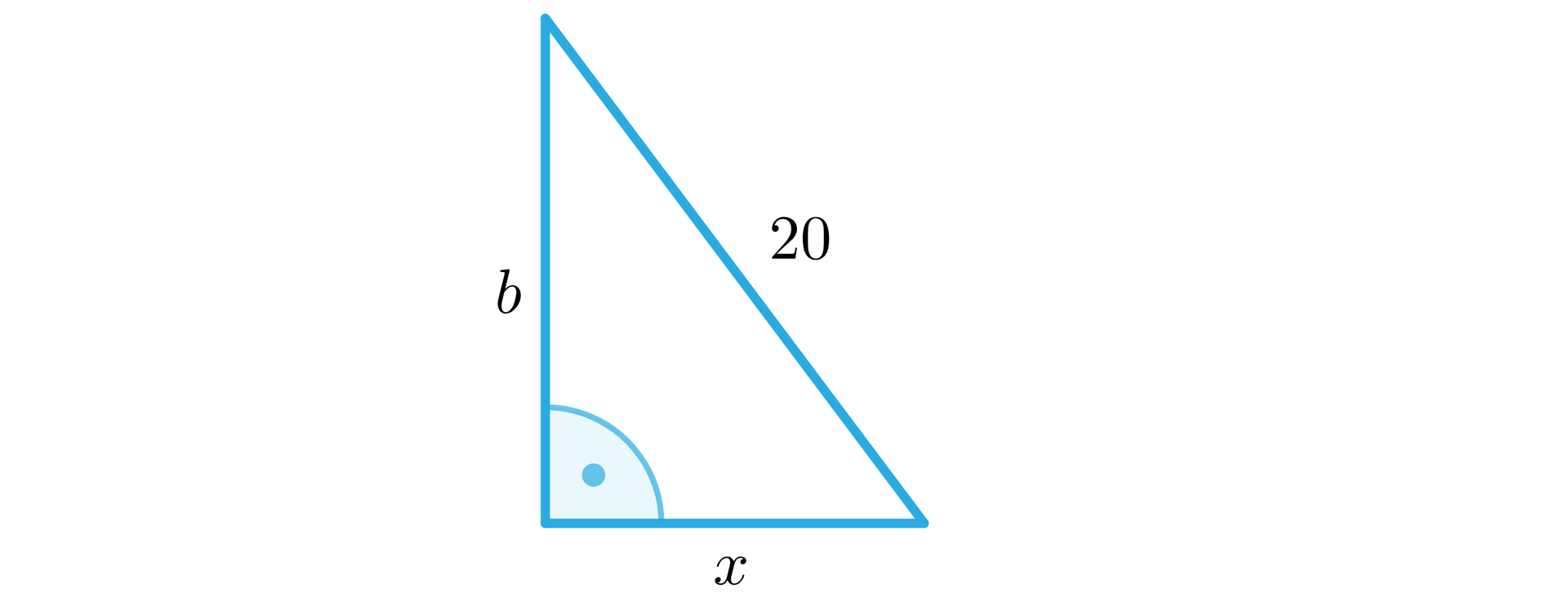
Ilustracja przedstawia trójkąt prostokątny z przyprostokątnymi o długości b oraz x oraz z przeciwprostokątną o długości dwadzieścia.

Rozwiązanie:

Z twierdzenia Pitagorasa dla trójkąta prostokątnego przedstawionego na rysunku mamy: $x^{2} + b^{2} = 20^{2}$ .

Z treści zadania mamy, że $\frac{b}{x} = \frac{4}{3}$ .

$b = \frac{4}{3} x$ , $0 < x < 20$

$x^{2} + {(\frac{4}{3} x)}^{2} = 20^{2}$

$x^{2} + \frac{16}{9} x^{2} = 20^{2}$

$\frac{25}{9} x^{2} = 20^{2}$

$\frac{25}{9} x^{2} - 20^{2} = 0$

$(\frac{5}{3} x - 20) (\frac{5}{3} x + 20) = 0$

Skorzystaliśmy ze wzoru na różnicę kwadratów: $a^{2} - b^{2} = (a - b) (a + b)$ .

Iloczyn jest równy zero, gdy jeden z czynników jest równy zero.

$\frac{5}{3} x - 20 = 0$ lub $\frac{5}{3} x + 20 = 0$

$\frac{5}{3} x = 20$ lub $\frac{5}{3} x = - 20$

$x = 12$ lub $x = - 12 < 0$

Długość boku nie może być ujemna,i musi spełniać zakładane wcześniej warunki, więc $x = 12$ .

$b = \frac{4}{3} x = \frac{4}{3} \cdot 12 = 16$

Odp.: Przyprostokątne mają długości $12 cm$ i $16 cm$ .

Przykład 3

Środki boków prostokąta o obwodzie równym $28 cm$ są wierzchołkami rombu o boku $5 cm$ . Wyznacz długości boków tego prostokąta.

R1cqzvmZnpuyY

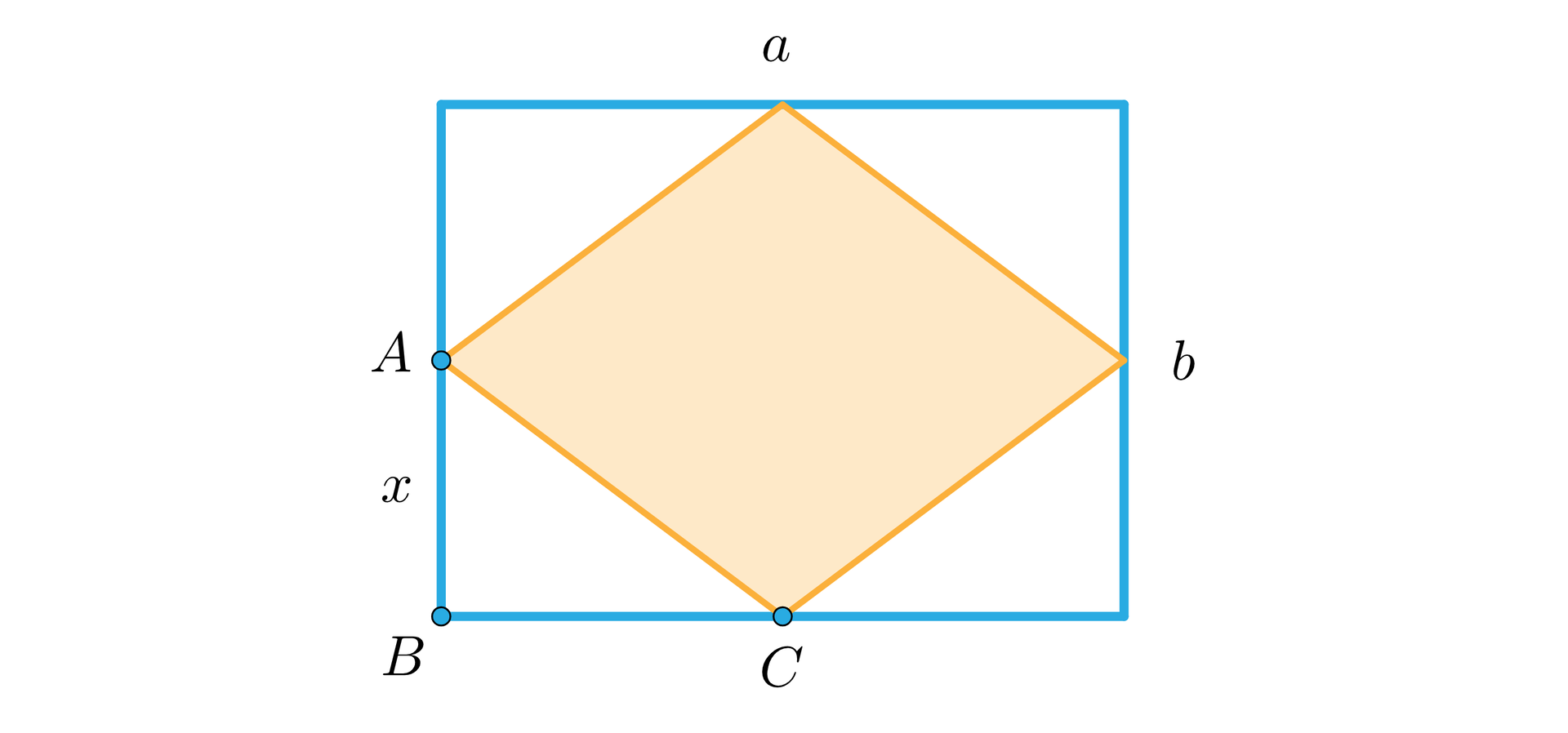
Ilustracja przedstawia prostokąt o wymiarach b na a oraz romb wpisany w prostokąt. Wierzchołek rombu A znajduje się na środku krótszego boku b prostokąta i tworzy odcinek A B, gdzie b to wierzchołek prostokąta, o długości x. Na środku dłuższego odcinka prostokąta o długości a, znajduje się wierzchołek rombu C.

Rozwiązanie:

Przyjmijmy oznaczenia, jak na rysunku.

Z treści zadania: $2 a + 2 b = 28$ .

$a + b = 14$

$a = 14 - b$

$b = 2 x$ , $0 < x < 7$

$a = 14 - 2 x$

Ponieważ środki boków prostokąta są wierzchołkami rombu, to powstały trójkąt $A B C$ jest trójkątem prostokątnym o przyprostokątnych długości $\frac{1}{2} b$ , $\frac{1}{2} a$ i przeciwprostokątnej o długości równej $5$ .

Możemy dla tego trójkąta zastosować twierdzenie Pitagorasa.

${(\frac{b}{2})}^{2} + {(\frac{a}{2})}^{2} = 5^{2}$

${(\frac{2 x}{2})}^{2} + {(\frac{14 - 2 x}{2})}^{2} = 25$

$x^{2} + {(7 - x)}^{2} = 25$

$x^{2} + 49 - 14 x + x^{2} = 25$

$2 x^{2} - 14 x + 24 = 0 | : 2$

$x^{2} - 7 x + 12 = 0$

Obliczamy wyróżnik trójmianu kwadratowego, aby znaleźć miejsca zerowe odpowiedniej funkcji kwadratowej.

$∆ = b^{2} - 4 a c = 7^{2} - 4 \cdot 1 \cdot 12 = 49 - 48 = 1$

$\sqrt{∆} = 1$

$x_{1} = \frac{- b + \sqrt{∆}}{2 a} = \frac{- (- 7) + \sqrt{1}}{2 \cdot 1} = \frac{7 + 1}{2} = \frac{8}{2} = 4$

$x_{2} = \frac{- b - \sqrt{∆}}{2 a} = \frac{- (- 7) - \sqrt{1}}{2 \cdot 1} = \frac{7 - 1}{2} = \frac{6}{2} = 3$

Dla $x_{1}$ mamy następujące rozwiązania:

$b_{1} = 2 x_{1} = 2 \cdot 4 = 8$

oraz

$a_{1} = 14 - b_{1} = 14 - 8 = 6$ .

Dla $x_{2}$ mamy następujące rozwiązania:

$b_{2} = 2 x_{2} = 2 \cdot 3 = 6$

oraz

$a_{2} = 14 - b_{2} = 14 - 6 = 8$ .

Odp.: Prostokąt ma boki o długościach $6 cm$ i $8 cm$ .

Przykład 4

Suma objętości dwóch sześcianów wynosi $72 {cm}^{3}$ , a suma ich wysokości wynosi $6 cm$ . Oblicz długość boku każdego z tych sześcianów.

Rozwiązanie:

Oznaczmy przez $x$ długość krawędzi jednego z sześcianów. Z treści zadania wynika, że krawędź drugiego sześcianu wynosi $6 - x$ .

R119QIGuNf0ng

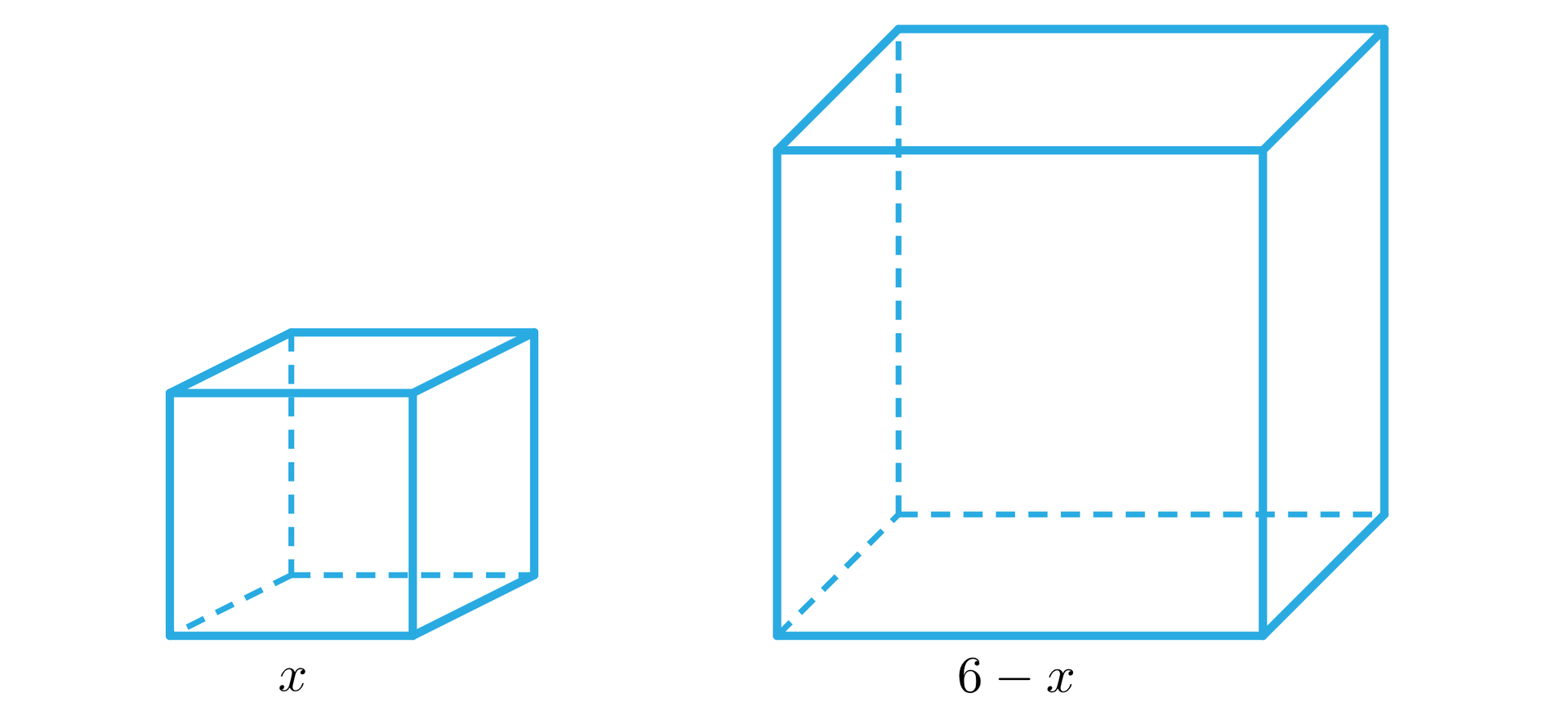
Ilustracja przedstawia dwa sześciany, pierwszy mniejszy o krawędzi równej x oraz drugi większy o krawędzi równej sześć odjąć x.

Objętość sześcianu wyraża wzór: $V = a^{3}$ .

Objętość pierwszego sześcianu: $V_{1} = x^{3}$ .

Objętość drugiego sześcianu: $V_{2} = {(6 - x)}^{3}$ , $0 < x < 6$ .

Z treści zadania: $V_{1} + V_{2} = 72$ .

Po podstawieniu $V_{1} = x^{3}$ i $V_{2} = {(6 - x)}^{3}$ , otrzymujemy wzór skróconego mnożenia na sumę sześcianów: $x^{3} + {(6 - x)}^{3} = 72$ .

Lewą stronę tego równania przekształcimy, wykorzystując wzór skróconego mnożenia na sumę sześcianów: $a^{3} + b^{3} = (a + b) (a^{2} - ab + b^{2})$ .

$x^{3} + {(6 - x)}^{3} = 72$

$(x + 6 - x) [x^{2} - x (6 - x) + {(6 - x)}^{2}] = 72$

Dzielimy stronami przez $6$ i przeprowadzamy redukcję wyrażeń podobnych.

$6 (x^{2} - 6 x + x^{2} + 36 - 12 x + x^{2}) = 72 | : 6$

$3 x^{2} - 18 x + 36 = 12$

$3 x^{2} - 18 x + 24 = 0 | : 3$

$x^{2} - 6 x + 8 = 0$

Wyznaczamy wyróżnik trójmianu kwadratowego oraz miejsca zerowe odpowiedniej funkcji.

$∆ = b^{2} - 4 a c = 36 - 4 \cdot 1 \cdot 8 = 36 - 32 = 4$

$\sqrt{∆} = \sqrt{4} = 2$

$x_{1} = \frac{- b + \sqrt{∆}}{2 a} = \frac{- (- 6) + \sqrt{4}}{2 \cdot 1} = \frac{6 + 2}{2} = \frac{8}{2} = 4$

Dla $x_{1} = 4$ bok drugiego sześcianu wynosi $6 - 4 = 2$ .

$x_{2} = \frac{- b - \sqrt{∆}}{2 a} = \frac{- (- 6) - \sqrt{4}}{2 \cdot 1} = \frac{6 - 2}{2} = \frac{4}{2} = 2$

Dla $x_{2} = 2$ bok drugiego sześcianu wynosi $6 - 2 = 4$ .

Odp.: Długości boków są równe $4 cm$ i $2 cm$ .

Słownik

funkcja kwadratowa

funkcję $f (x) = a x^{2} + b x + c$ określoną dla wszystkich liczb rzeczywistych, gdzie $a$ , $b$ , $c$ są liczbami rzeczywistymi, przy czym $a \neq 0$ , nazywamy funkcją kwadratową

Wprowadzenie

Animacja

Słownik