Przeczytaj

Jeżeli funkcja $g$ odwzorowuje zbiór $X$ w zbiór $Y$ , a funkcja $f$ odwzorowuje zbiór $Y$ w zbiór $Z$ , to funkcję $h$ określoną wzorem $h (x) = f (g (x))$ dla $x \in X$ nazywamy złożeniem funkcji $g$ i $f$ i oznaczamy $f \circ g$ .

Funkcję $g$ nazywamy funkcją wewnętrzną funkcji $f \circ g$ natomiast funkcję $f$ nazywamy funkcją zewnętrzną funkcji $f \circ g$ .

Jeżeli istnieje złożenie funkcjifunkcja złożonazłożenie funkcji $f$ z funkcją $g$ to jest ono wyznaczone jednoznacznie.

Przykład 1

Przedstawmy złożenie funkcji $f (x) = x^{2}$ i $g (x) = 2 x + 4$
jako $h (x) = f (g (x))$ .

Funkcja wewnętrzna to $g (x) = 2 x + 4$ , gdzie $D_{g} = ℝ$ i $g (D_{g}) = ℝ$ .

Funkcja zewnętrzna to $f (x) = x^{2}$ , gdzie $D_{f} = ℝ$ i $g (D_{g}) \subset D_{f}$ .

Istnieje więc złożenie $h (x) = f (g (x))$ , gdzie $h (x) = f (g (x)) = f (2 x + 4) = {(2 x + 4)}^{2}$ dla każdego $x \in ℝ$ .

Gdy daną funkcję $h$ traktujemy jako złożenie dwóch funkcji $f$ i $g$ , to funkcje $f$ i $g$ nie są wyznaczone jednoznacznie przez funkcję $h$ .

Przykład 2

Funkcję $h$ określoną wzorem $h (x) = {(2 x + 4)}^{2}$ przedstaw jako złożenie dwóch funkcji.

Rozwiązanie:

Funkcję $h (x) = {(2 x + 4)}^{2}$ możemy zapisać następująco:

$h (x) = {(2 x + 4)}^{2} = {(2 x)}^{2} + 8 (2 x) + 16 =$
$= 4 x^{2} + 16 x + 16 = 4 (x^{2} + 4 x + 4) = 4 {(x + 2)}^{2}$

Wykorzystując powyższy zapis, otrzymujemy:

a) $h (x) = {(2 x + 4)}^{2}$ , $x \in ℝ$ .

$h (x) = f_{1} (g_{1} (x)) = f_{1} (2 x + 4) = {(2 x + 4)}^{2}$ .

Funkcja zewnętrzna to $f_{1} (x) = x^{2}$ , a funkcja wewnętrzna $g_{1} (x) = 2 x + 4$ .

b) $h (x) = {(2 x)}^{2} + 8 (2 x) + 16$ , $x \in ℝ$ .

$h (x) = f_{2} (g_{2} (x)) = f_{2} (2 x) = {(2 x)}^{2} + 8 (2 x) + 16$ .

Funkcja zewnętrzna to $f_{2} (x) = x^{2} + 8 x + 16$ , a funkcja wewnętrzna: $g_{2} (x) = 2 x$ .

c) $h (x) = 4 {(x + 2)}^{2}$ , $x \in ℝ$ .

$h (x) = f_{3} (g_{3} (x)) = f_{3} (x + 2) = 4 {(x + 2)}^{2}$ .

Funkcja zewnętrzna to $f_{3} (x) = 4 x^{2}$ , a funkcja wewnętrzna $g_{3} (x) = x + 2$ .

Nie są to wszystkie możliwe przedstawienia funkcji $f$ w postaci złożenia dwóch funkcji. Takich przedstawień jest nieskończenie wiele.

Przykład 3

Funkcję $h$ określoną wzorem $h (x) = 2^{x^{2} - 5 x - 4}$ przedstaw w postaci złożenia dwóch funkcji.

Rozwiązanie:

$h (x) = 2^{x^{2} - 5 x - 4}$ .

$D_{h} = ℝ$ .

$h (x) = f (g (x)) = f (x^{2} - 5 x - 4) = 2^{x^{2} - 5 x - 4}$ .

Funkcja zewnętrzna to $f (x) = 2^{x}$ , a funkcja wewnętrzna $g (x) = x^{2} - 5 x - 4$ .

Przykład 4

Funkcję $h$ określoną wzorem $h (x) = \log_{2} \sqrt{x^{2} - 3 x}$ przedstaw na dwa sposoby w postaci złożenia dwóch funkcji.

Rozwiązanie:

Określmy dziedzinę funkcji $h (x) = \log_{2} \sqrt{x^{2} - 3 x}$ .

Dziedziną funkcji logarytmicznej $y = \log_{a} x$ jest zbiór $ℝ_{+}$ więc:

$\sqrt{x^{2} - 3 x} > 0$ , skąd $x^{2} - 3 x > 0$ , a następnie $x (x - 3) > 0$ .

R431yIIm8YRSv

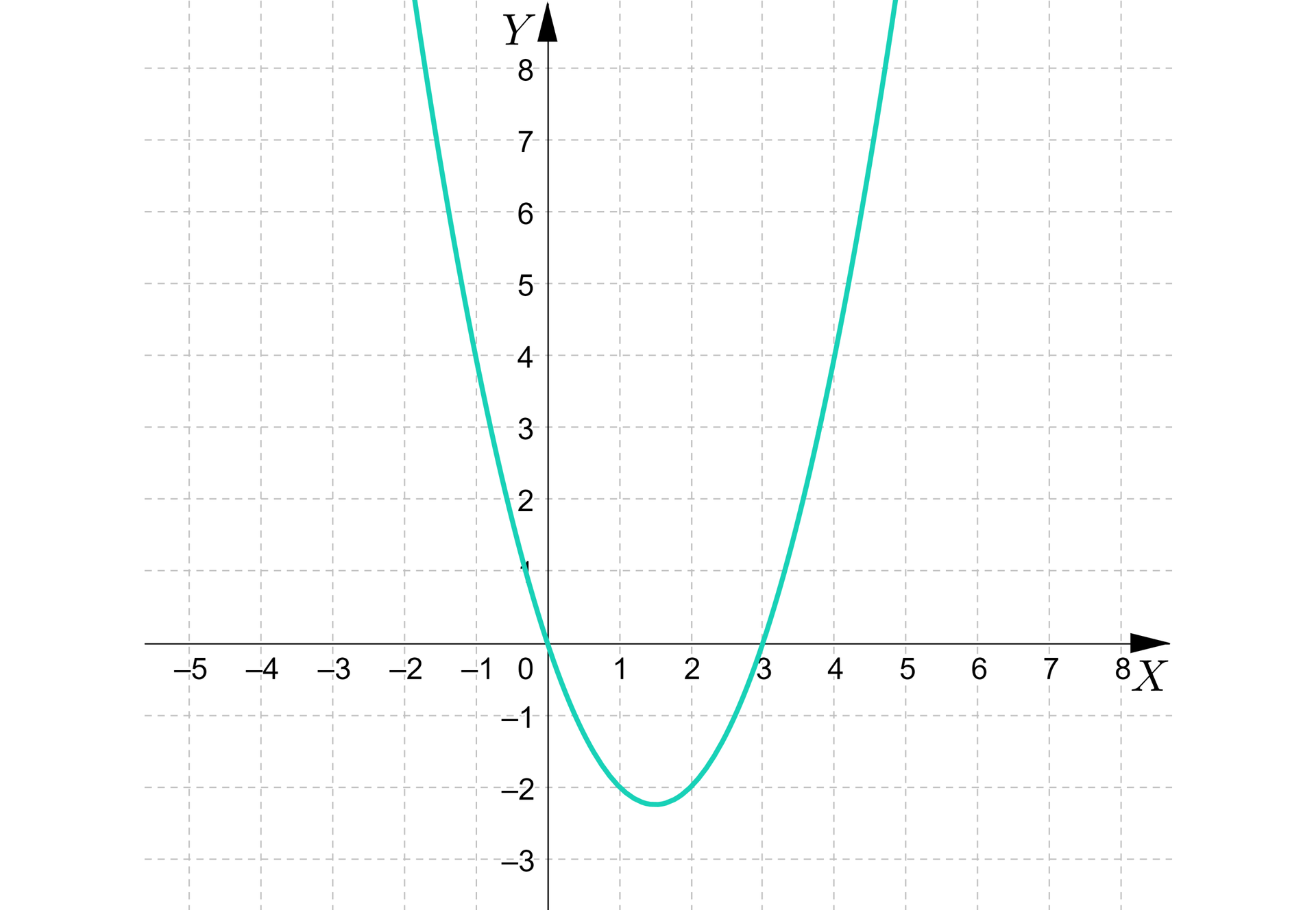
Ilustracja przedstawia układ współrzędnych z poziomą osią X od minus pięciu do ośmiu i pionową osią Y od minus trzech do ośmiu. W układzie współrzędnych zaznaczono parabolę z ramionami skierowanymi do góry posiadająca dwa miejsca zerowe. Przechodzi ona przez takie punkty jak: nawias zero przecinek zero zamknięcie nawiasu, nawias jeden przecinek minus dwa zamknięcie nawiasu, nawias dwa przecinek minus dwa zamknięcie nawiasu, nawias trzy przecinek zero zamknięcie nawiasu oraz nawias cztery przecinek cztery zamknięcie nawiasu.

Zbiorem rozwiązań nierówności $x (x - 3) > 0$ jest:

$x \in (- \infty, 0) \cup (3, + \infty)$ , a zatem

$D_{h} = (- \infty, 0) \cup (3, + \infty)$ .

$h (x) = f_{1} (g_{1} (x)) = f (\sqrt{x^{2} - 3 x}) = \log_{2} \sqrt{x^{2} - 3 x}$ , $x \in (- \infty, 0) \cup (3, + \infty)$ .

Funkcja zewnętrzna to zatem $f_{1} (x) = \log_{2} x$ , a funkcja wewnętrzna $g_{1} (x) = \sqrt{x^{2} - 3 x}$ .

$h (x) = f_{2} (g_{2} (x)) = f (x^{2} - 3 x) = \log_{2} \sqrt{x^{2} - 3 x}$ , $x \in (- \infty, 0) \cup (3, + \infty)$

Funkcja zewnętrzna to $f_{1} (x) = \log_{2} \sqrt{x}$ , a funkcja wewnętrzna $g_{2} (x) = x^{2} - 3 x$ .

Słownik

funkcja złożona

funkcja $h$ określona wzorem $h (x) = f (g (x))$ dla $x \in X$ , gdy funkcja $g$ odwzorowuje zbiór $X$ w zbiór $Y$ , a funkcja $f$ odwzorowuje zbiór $Y$ w zbiór $Z$

Wprowadzenie

Animacja

Słownik