Wykażemy, że długość wysokości opuszczonej na przeciwprostokątną w trójkącie prostokątnym o przyprostokątnych długości $a$ i $b$ jest równa $h=\frac{a·b}{\sqrt{a^2+b^2}}$.

Rozwiązanie

Przyjmijmy oznaczenia: $\left|\sphericalangle ACB\right|=90°$; $a$, $b$ – długości przyprostokątnych; $c$ – długość przeciwprostokątnej.

Zastosujemy $2$ wzory na pole trójkąta:

Rzn04N6dq5tPp

Ilustracja przedstawia dwa trójkąty prostokątne. Pierwszy ABC o ramieniu AB o długości c, o ramieniu CB długości a oraz ramieniu AC o długości b. Z wierzchołka C upuszczono wysokość na podstawę AB. Drugi trójkąt prostokątny ABC o ramionach: AB o długości c, następnie AC o długości b oraz BC o długości a.

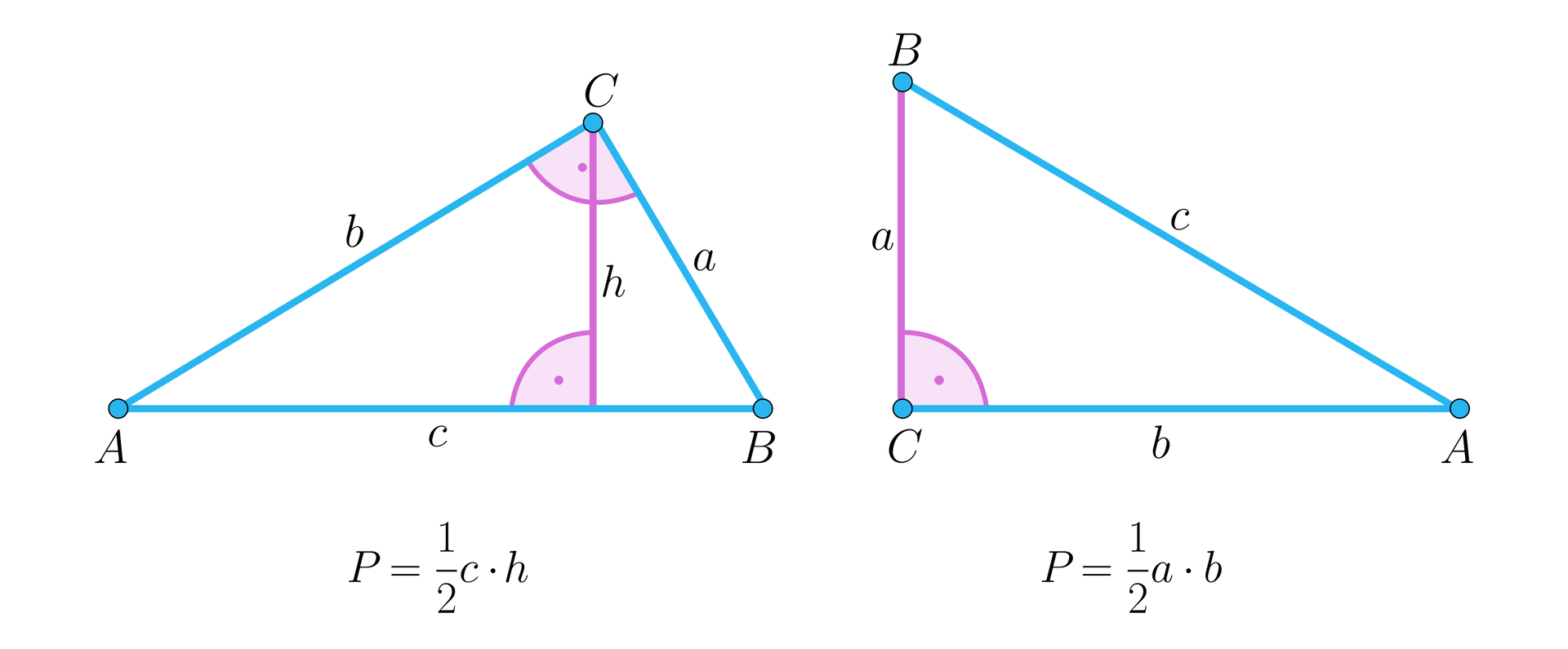
Porównujemy pola trójkąta, wyliczając wysokość:

$\frac{1}{2}c·h=\frac{1}{2}a·b$ stąd $h=\frac{a·b}{c}$.

Z twierdzenia Pitagorasa wyliczamy $c$:

$c^2=a^2+b^2$ stąd $c=\sqrt{a^2+b^2}$.

Zatem:

$h=\frac{a·b}{\sqrt{a^2+b^2}}$.

Wykazaliśmy, że długość wysokości opuszczonej na przeciwprostokątną w trójkącie prostokątnym o przyprostokątnych długości $a$ i $b$ jest równa: $h=\frac{a·b}{\sqrt{a^2+b^2}}$.

W trójkącie $ABC$ boki $BC$ i $AC$ mają długości odpowiednio $4$ i $2$, kąt przy wierzchołku $C$ ma miarę $120°$. Wykażemy, że długość odcinka dwusiecznejdwusieczna kąta trójkątadwusiecznej kątadwusieczna kąta trójkątakąta $ACB$, który jest zawarty w trójkącie $ABC$, wynosi $\frac{4}{3}$.

Rozwiązanie

R17GJvKuvwLes

Ilustracja przedstawia trójkąt ABC o kącie przy wierzchołku C o mierze 120 stopni. Odcinek CD wynosi d, gdzie punkt D znajduje się na podstawie AB.

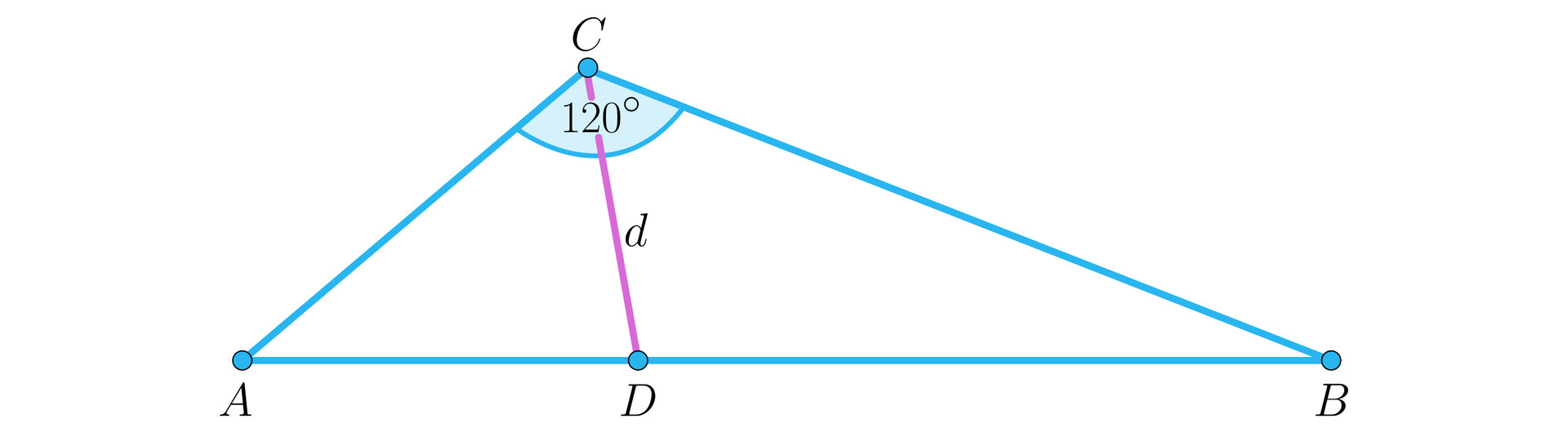
Niech $d=\left|CD\right|$ będzie szukaną długością odcinka dwusiecznej kątadwusieczna kątadwusiecznej kąta $ACB$.

Z treści zadania: $\left|BC\right|=4$, $\left|AC\right|=2$ i $\left|\sphericalangle ACB\right|=120°$.

Skoro $CD$ jest dwusieczną kąta $ACB$, to: $\left|\sphericalangle ACD\right|=\left|\sphericalangle DCB\right|=60°$.

Zauważmy, że: $P_{△ABC}=P_{△ADC}+P_{△DBC}$.

Skorzystamy ze wzoru na pole trójkąta postaci: $P=\frac{1}{2}a·b·\sin \alpha$, gdzie $a, b$ - długości boków trójkąta, zaś $\alpha$ - miara kąta zawartego między tymi bokami.

Mamy zatem:

$P_{△ABC}=\frac{1}{2}\left|AC\right|·\left|BC\right|·\sin \left(\sphericalangle ACB\right)$

$P_{△ABC}=\frac{1}{2}·2·4·\sin 120°=4·\sin \left(180°-60°\right)=4·\sin 60°$,

$P_{△ADC}=\frac{1}{2}·\left|AC\right|·\left|CD\right|·\sin \left(\sphericalangle ACD\right)$

$P_{△ADC}=\frac{1}{2}·2·d·\sin 60°=d·\sin 60°$,

$P_{△DBC}=\frac{1}{2}·\left|CD\right|·\left|BC\right|·\sin \left(\sphericalangle DCB\right)$

$P_{△DBC}=\frac{1}{2}·d·4·\sin 60°=2·d·\sin 60°$.

Po podstawieniu dostajemy równanie:

$4·\sin 60°=d·\sin 60°+2·d·\sin 60°$.

Dzielimy obie strony równania przez $\sin 60°$ i otrzymujemy:

$4=d+2d$

$4=3d$, stąd $d=\frac{4}{3}$.

Długość odcinka dwusiecznej kąta $ACB$, który jest zawarty w trójkącie $ABC$ wynosi $\frac{4}{3}$, co należało udowodnić.

Niech $a$, $b$, $c$ oznaczają długości boków trójkąta. Mając dane $a$ i $b$ oraz wiedząc, że suma długości wysokości opuszczonych na boki $a$ i $b$ jest równa długości trzeciej wysokości trójkąta, wykażemy, że $c=\frac{a·b}{a+b}$.

RN9xOzJNMNryp

Ilustracja przedstawia trójkąt ABC. Ramię AB o długości c, ramią AC o długości b oraz ramią BC o długości a. Zaznaczono przekątne wychodzące z każdego wierzchołka h indeks dolny a koniec indeksu. h indeks dolny b koniec indeksu. h indeks dolny c koniec indeksu. Wysokości przecinają się w jednym punkcie.

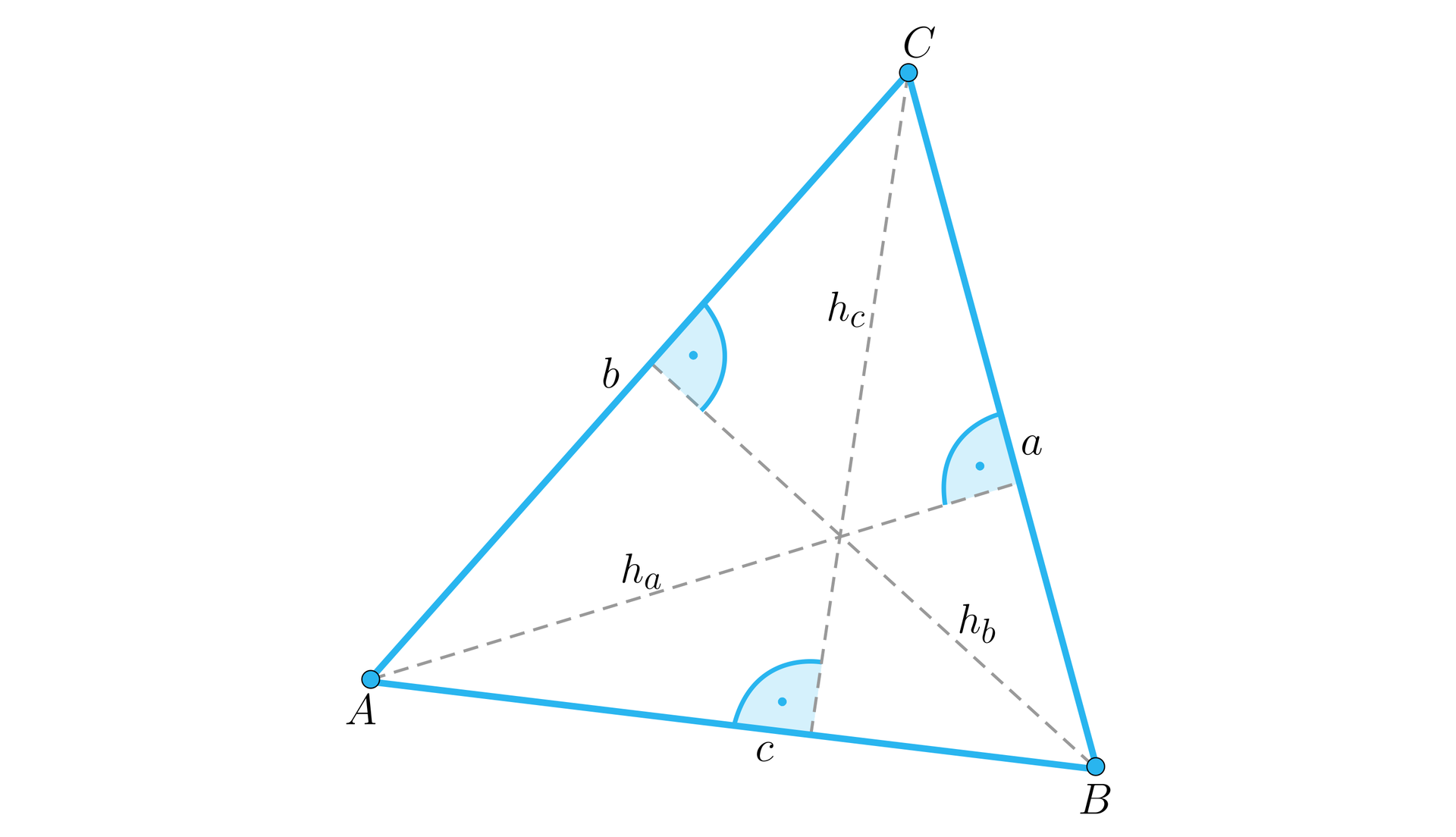
Rozwiązanie

Pole tego trójkąta możemy zapisać następująco:

$P=\frac{1}{2}a·h_a$ lub $P=\frac{1}{2}b·h_b$ lub $P=\frac{1}{2}c·h_c$.

Z porównania pól: $P=\frac{1}{2}a·h_a$ i $P=\frac{1}{2}b·h_b$ otrzymujemy: $\frac{1}{2}a·h_a=\frac{1}{2}b·h_b$, co możemy zapisać w postaci: $\frac{h_a}{h_b}=\frac{b}{a}$.

Ponadto $\frac{1}{2}a·h_a+\frac{1}{2}b·h_b=2·\frac{1}{2}c·h_c$, zatem: $a·h_a+b·h_b=2c·h_c$.

Z treści zadania $h_c=h_a+h_b$, więc: $a·h_a+b·h_b=2c\left(h_a+h_b\right)$.

Dzielimy obie strony równanie przez $h_b$:

$a·\frac{h_a}{h_b}+b·\frac{h_b}{h_b}=2c\left(\frac{h_a}{h_b}+\frac{h_b}{h_b}\right)$

$a·\frac{h_a}{h_b}+b=2c\left(\frac{h_a}{h_b}+1\right)$.

Skoro $\frac{h_a}{h_b}=\frac{b}{a}$, to:

$a·\frac{b}{a}+b=2c\left(\frac{b}{a}+1\right)$

$b+b=2c\left(\frac{b}{a}+1\right)$

$b=c\left(\frac{b}{a}+\frac{a}{a}\right)$

$b=c·\frac{b+a}{a}$

$c=\frac{a·b}{b+a}$.

Wykazaliśmy zatem, że $c=\frac{a·b}{b+a}$.

Punkt $O$ leży wewnątrz trójkąta $ABC$. Odległości tego punktu od boków trójkątaodległość punktu od boku trójkątaOdległości tego punktu od boków trójkąta są odpowiednio równe $x$, $y$, $z$, a odpowiednie wysokości trójkąta $ABC$ mają długości $h_1$, $h_2$, $h_3$. Udowodnimy, że: $\frac{x}{h_1}+\frac{y}{h_2}+\frac{z}{h_3}=1$.

RMGgLZbPMJRHW

Ilustracja przedstawia trójkąt ostrokątny A B C. Z każdego wierzchołka upuszczono wysokość na przeciwległy bok: z wierzchołka A upuszczono wysokość h indeks dolny 3, z wierzchołka B upuszczono wysokość h indeks dolny 2, a z wierzchołka C upuszczono wysokość h indeks dolny 1; wysokości przecinają się w jednym punkcie. Wewnątrz trójkąta zaznaczono punkt, z którego linią przerywaną poprowadzono odległości między punktem O i każdym z boków. Najdłuższa odległość wynosi x, to odległość między punktem O a podstawą A B, odległość między punktem O a bokiem A  C wynosi y, a odległość między punktem O a bokiem B C wynosi z.

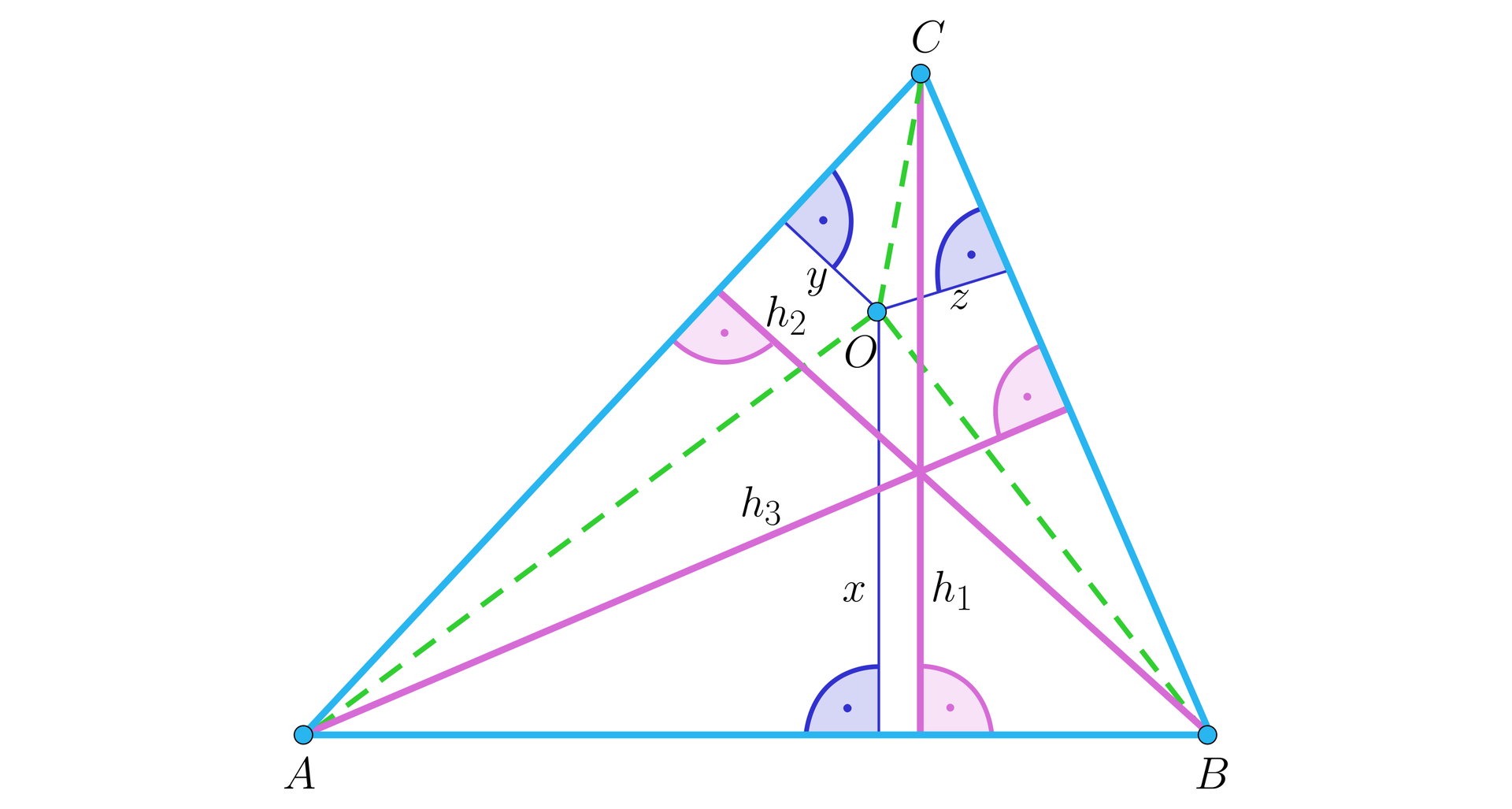
Rozwiązanie

Łączymy punkt $O$ z wierzchołkami trójkąta $ABC$. Otrzymujemy trzy trójkąty: $ABO$, $BCO$ i $CAO$.

Zauważmy, że:

$P_{△ABO}+P_{△BCO}+P_{△CAO}=P_{△ABC}$,

gdzie:

$P_{△ABO}=\frac{1}{2}\left|AB\right|·x$; $P_{△BCO}=\frac{1}{2}\left|CB\right|·z$; $P_{△CAO}=\frac{1}{2}\left|AC\right|·y$ i $P_{△ABC}=\frac{1}{2}\left|AB\right|·h_1$.

Mamy zatem:

$\frac{1}{2}\left|AB\right|·x+\frac{1}{2}\left|CB\right|·z+\frac{1}{2}\left|AC\right|·y=\frac{1}{2}\left|AB\right|·h_1$.

Dzielimy obie strony równania przez $\frac{1}{2}\left|AB\right|·h_1$ i otrzymujemy: $\frac{x}{h_1}+\frac{\left|CB\right|·z}{\left|AB\right|·h_1}+\frac{\left|AC\right|·y}{\left|AB\right|·h_1}=1$ (1).

Pole trójkąta $ABC$ może zapisać na trzy sposoby:

$P_{△ABC}=\frac{1}{2}\left|AB\right|·h_1=\frac{1}{2}\left|CA\right|·h_2=\frac{1}{2}\left|CB\right|·h_3$.

Wykorzystamy związki: $\frac{1}{2}\left|AB\right|·h_1=\frac{1}{2}\left|CA\right|·h_2$ oraz $\frac{1}{2}\left|AB\right|·h_1=\frac{1}{2}\left|CB\right|·h_3$.

Z równości: $\frac{1}{2}\left|AB\right|·h_1=\frac{1}{2}\left|CA\right|·h_2$ mamy $\left|AB\right|·h_1=\left|AC\right|·h_2$, 
czyli $\frac{h_1}{h_2}=\frac{\left|AC\right|}{\left|AB\right|}$ (2).

Z równości: $\frac{1}{2}\left|AB\right|·h_1=\frac{1}{2}\left|CB\right|·h_3$ mamy $\left|AB\right|·h_1=\left|CB\right|·h_3$, 
czyli $\frac{h_1}{h_3}=\frac{\left|CB\right|}{\left|AB\right|}$ (3).

Związki (2) i (3) podstawiamy do równości (1):

$\frac{x}{h_1}+\frac{\left|CB\right|}{\left|AB\right|}·\frac{z}{h_1}+\frac{\left|AC\right|}{\left|AB\right|}·\frac{y}{h_1}=1$

$\frac{x}{h_1}+\frac{h_1}{h_3}·\frac{z}{h_1}+\frac{h_1}{h_2}·\frac{y}{h_1}=1$

$\frac{x}{h_1}+\frac{z}{h_3}+\frac{y}{h_2}=1$.

Ostatecznie otrzymujemy: $\frac{x}{h_1}+\frac{y}{h_2}+\frac{z}{h_3}=1$, co należało udowodnić.

półprosta o początku w wierzchołku kąta i dzieląca ten kąt na dwa kąty przystające

odcinek, który jest częścią wspólną trójkąta i dwusiecznej kąta wewnętrznego tego trójkąta

długość odcinka prostopadłego do boku trójkąta, którego jednym końcem jest punkt $O$, który nie należy do rozważanego boku trójkąta, a drugim końcem jest punkt należący do tego boku