Przeczytaj

Omówimy przesunięcie paraboli, będącej wykresem funkcji kwadratowej określonej na zbiorze $ℝ$ wzorem $f (x) = a x^{2}$ , gdzie $a \in ℝ ∖ \{0\}$ , wzdłuż osi $Y$ układu współrzędnych.

przesunięcie wykresu funkcji wzdłuż osi

Y

Definicja: przesunięcie wykresu funkcji wzdłuż osi

Y

Wykres funkcji $f (x) + q$ otrzymano w wyniku:

przesunięcia wykresu funkcji $f$ wzdłuż osi $Y$ o $q$ jednostek w górę, gdy $q > 0$ ,
przesunięcia wykresu funkcji $f$ wzdłuż osi $Y$ o $q$ jednostek w dół, gdy $q < 0$ .

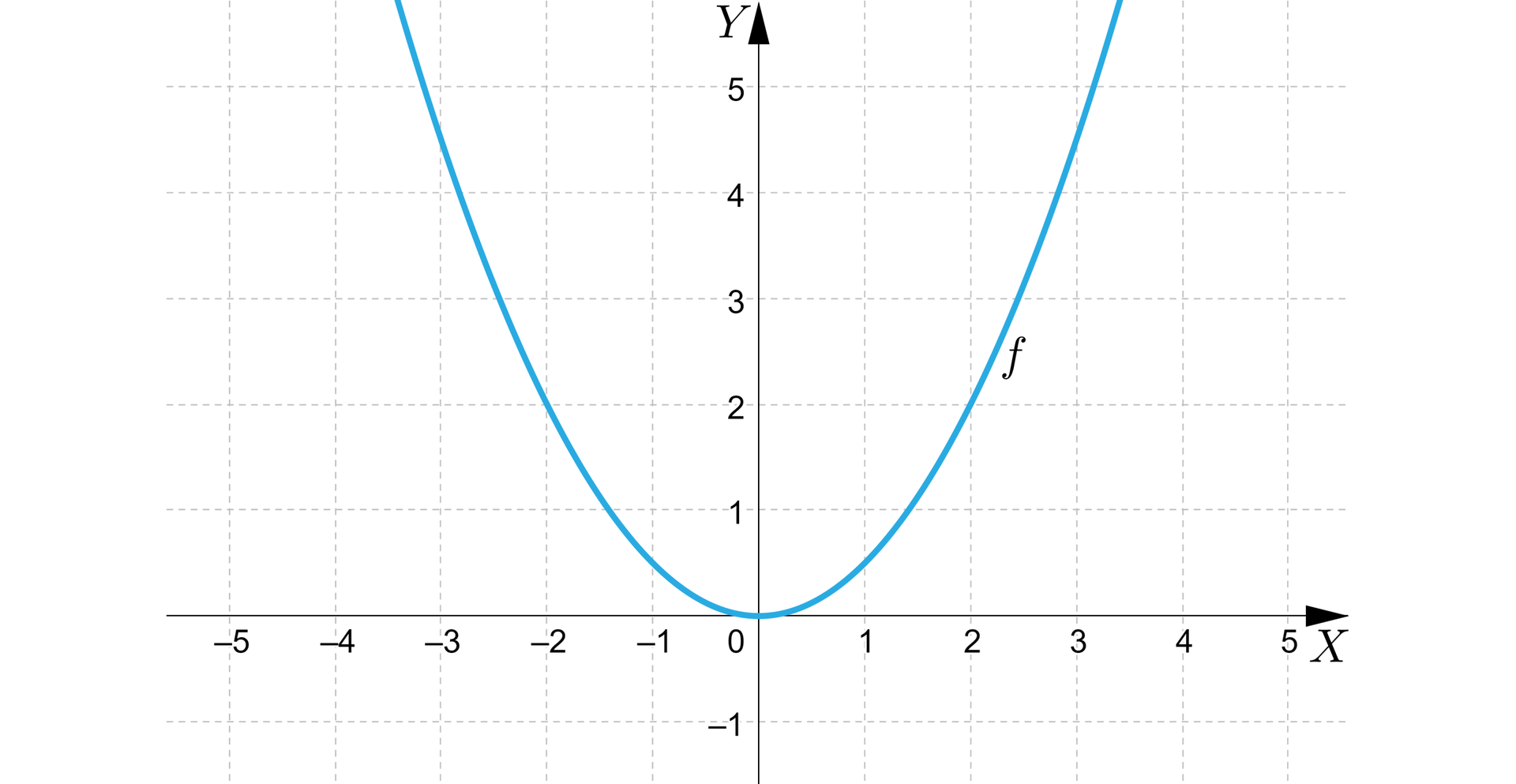
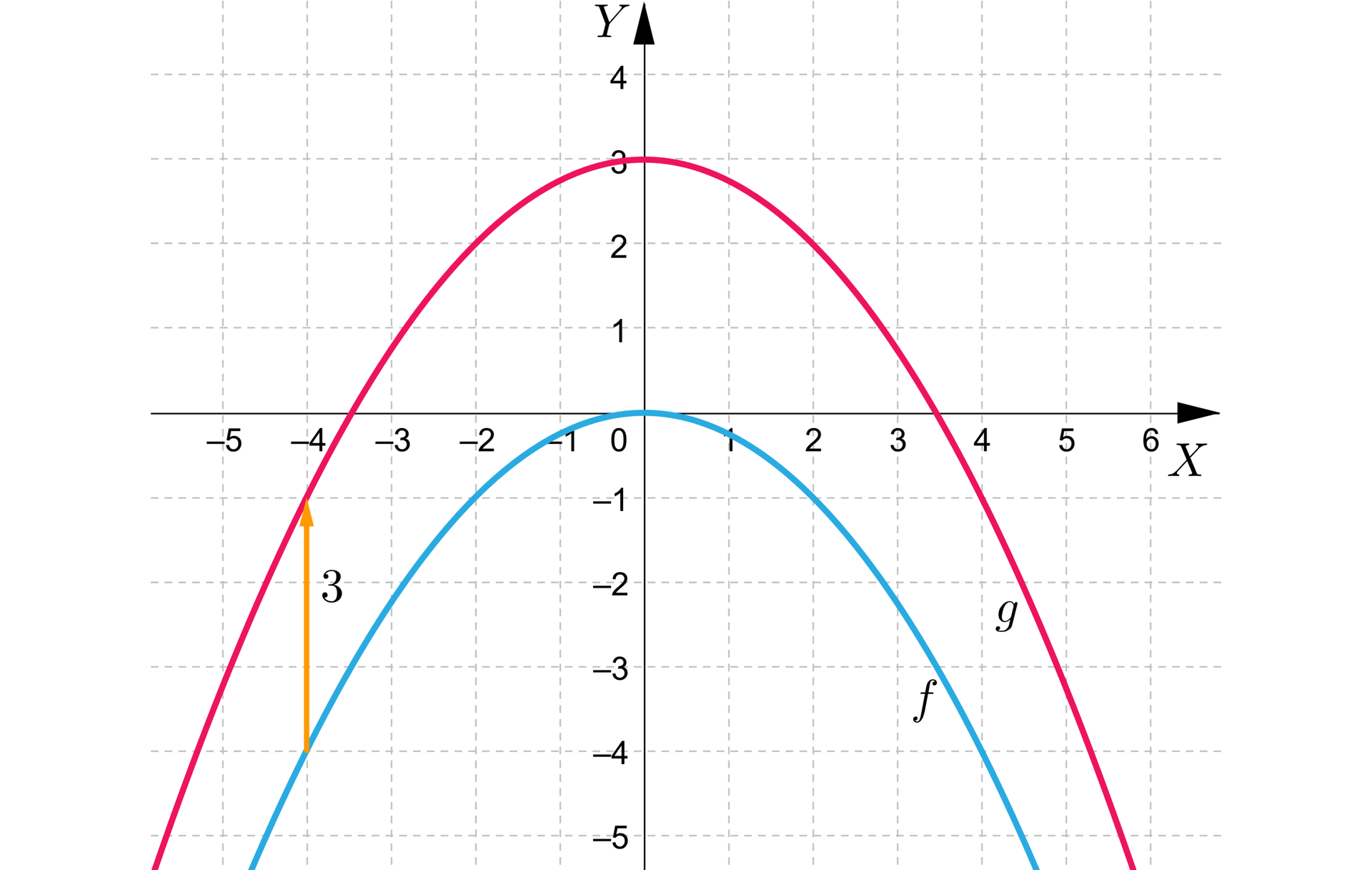
Sporządźmy wykres funkcji określonej wzorem $f (x) = \frac{1}{2} x^{2}$ .

W celu naszkicowania paraboli, będącej wykresem funkcji przedstawmy w tabeli wartości funkcji $f$ dla kilku argumentów:

$x$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$2$	$\frac{1}{2}$	$0$	$\frac{1}{2}$	$2$

Wykres funkcji $f$ przedstawia się następująco:

R1dQKtNJxjxN7

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od pięciu do pięciu oraz z pionową osią Y od minus jeden do pięciu. W układzie współrzędnych zaznaczono funkcję kwadratową f, której wykres jest parabolą z ramionami skierowanymi do góry oraz wierzchołkiem w początku układu współrzędnych. Parabola przechodzi przez punkty -2,2 oraz 2,2 .

Aby otrzymać wykres funkcji $g (x) = f (x) - 2$ , przesuniemy wykres funkcji f o $2$ jednostki w dół wzdłuż osi $Y$ .

Wykresy funkcji przedstawiają się następująco:

RVlTQpLy17QOi

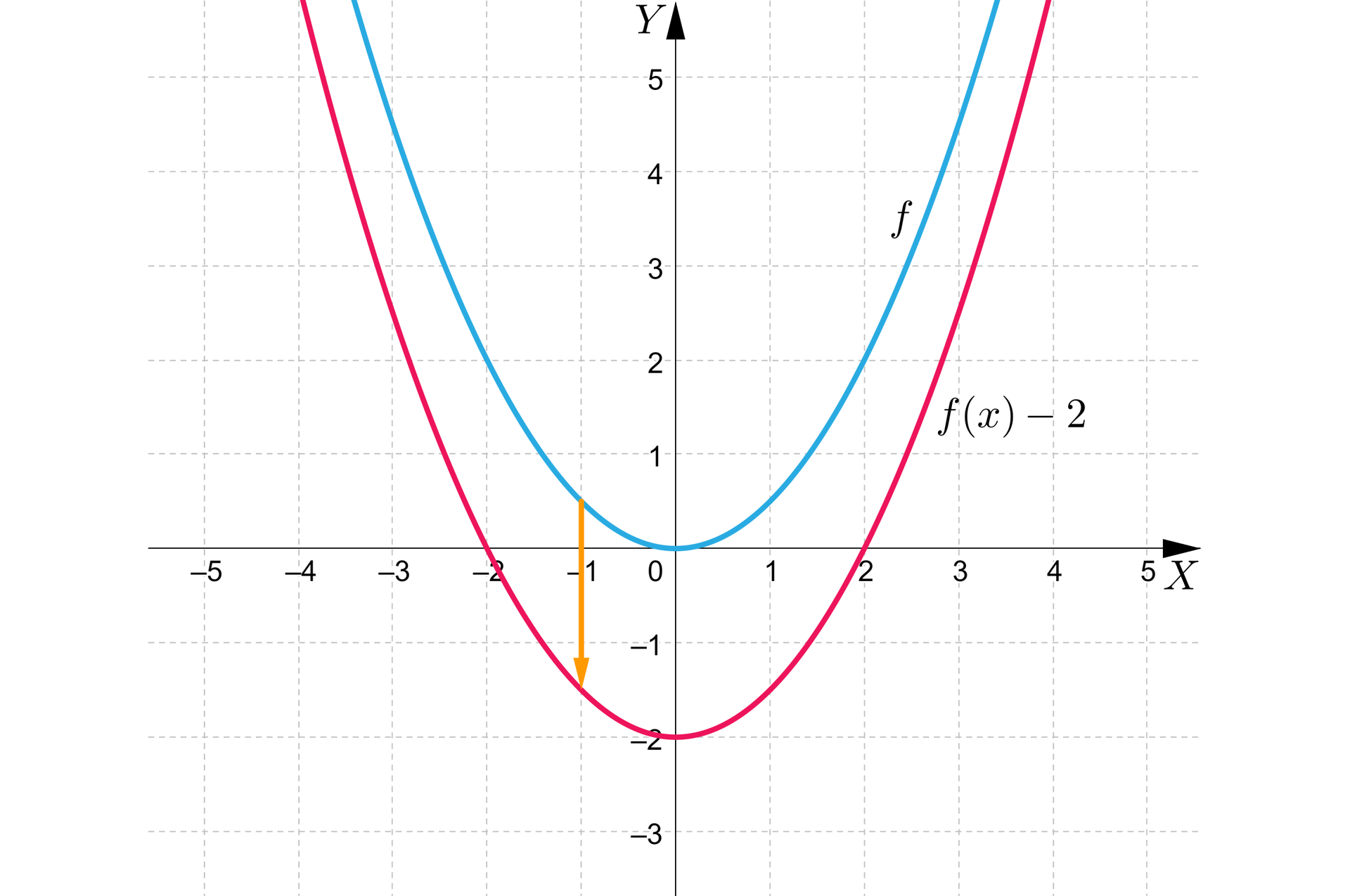
Funkcje f i g mają te same dziedziny oraz:

równanie osi symetrii ich wykresów to $x = 0$ ,
przedział, w którym funkcje są malejące to $(- \infty, 0⟩$ ,
przedział, w którym funkcje są rosnące to $⟨0, \infty)$ .

Zauważmy, że przy przesunięciu wykresu funkcji o $2$ jednostki w dół wzdłuż osi $Y$ :

zmienił się zbiór wartości funkcji, z przedziału $⟨0, \infty)$ na przedział $⟨- 2, \infty)$ ,
zmieniły się współrzędne wierzchołka paraboli, z punktu o współrzędnych $(0, 0)$ do punktu o współrzędnych $(0, - 2)$ ,
zmieniła się wartość najmniejsza funkcji, z liczby $0$ na liczbę $(- 2)$ dla argumentu $x = 0$ ,
funkcja $f$ ma jedno miejsce zerowe $0$ , a po przesunięciu jej wykresu o $2$ jednostki w dół wzdłuż osi $Y$ miejscami zerowymi otrzymanej funkcji są liczby $- 2$ oraz $2$ .

Jeżeli przesuwamy parabolę, będącą wykresem funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , gdzie $a > 0$ , wzdłuż osi $Y$ o $q$ jednostek w górę lub o $q$ jednostek w dół, otrzymując wykres funkcji g to:

zbiorem wartości funkcji g jest przedział $⟨q, \infty)$ ,
wierzchołkiem paraboli, która jest wykresem funkcji g jest punkt o współrzędnych $(0, q)$ ,
funkcja g osiąga wartość najmniejszą dla argumentu $x = 0$ wynoszącą $q$ .

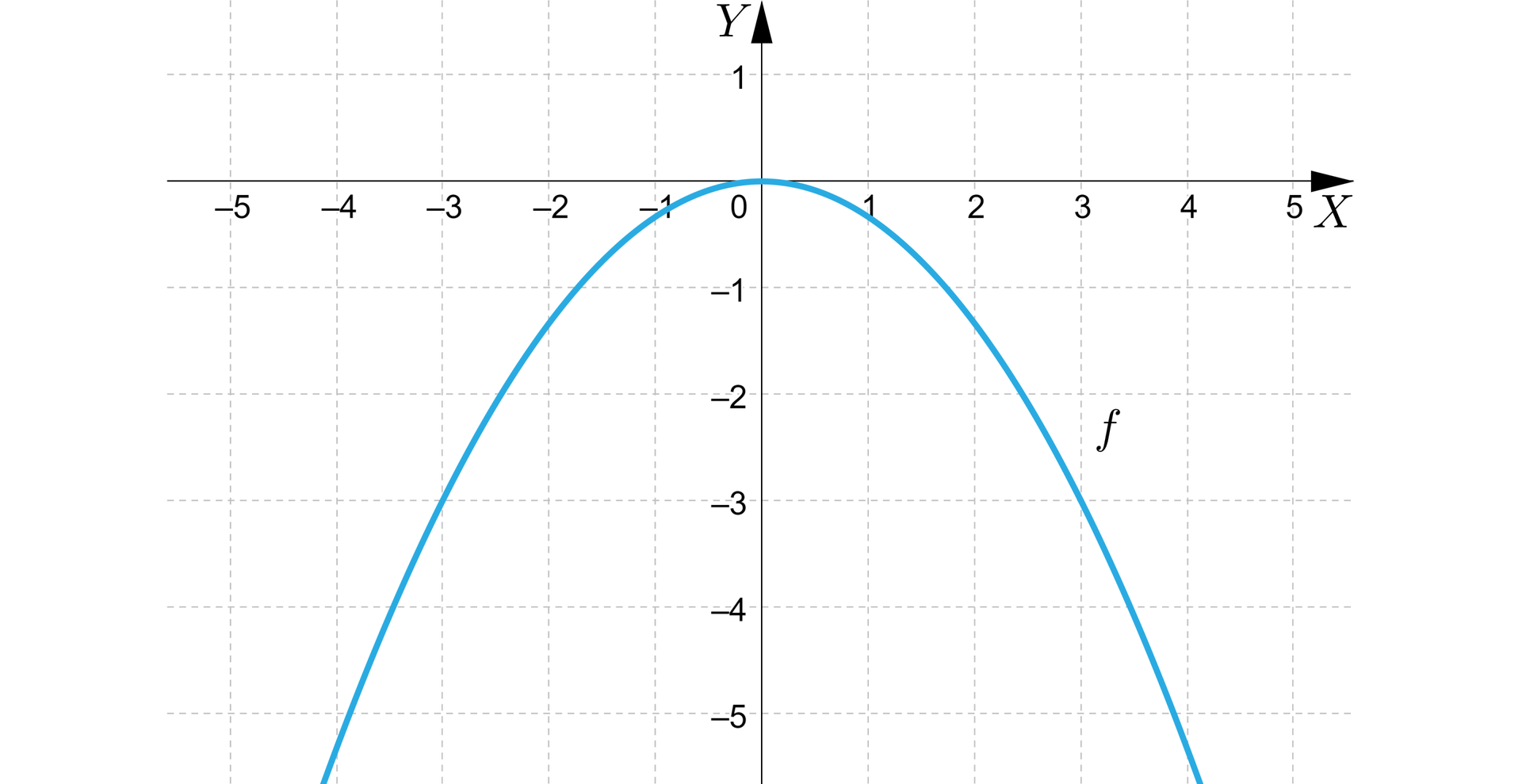
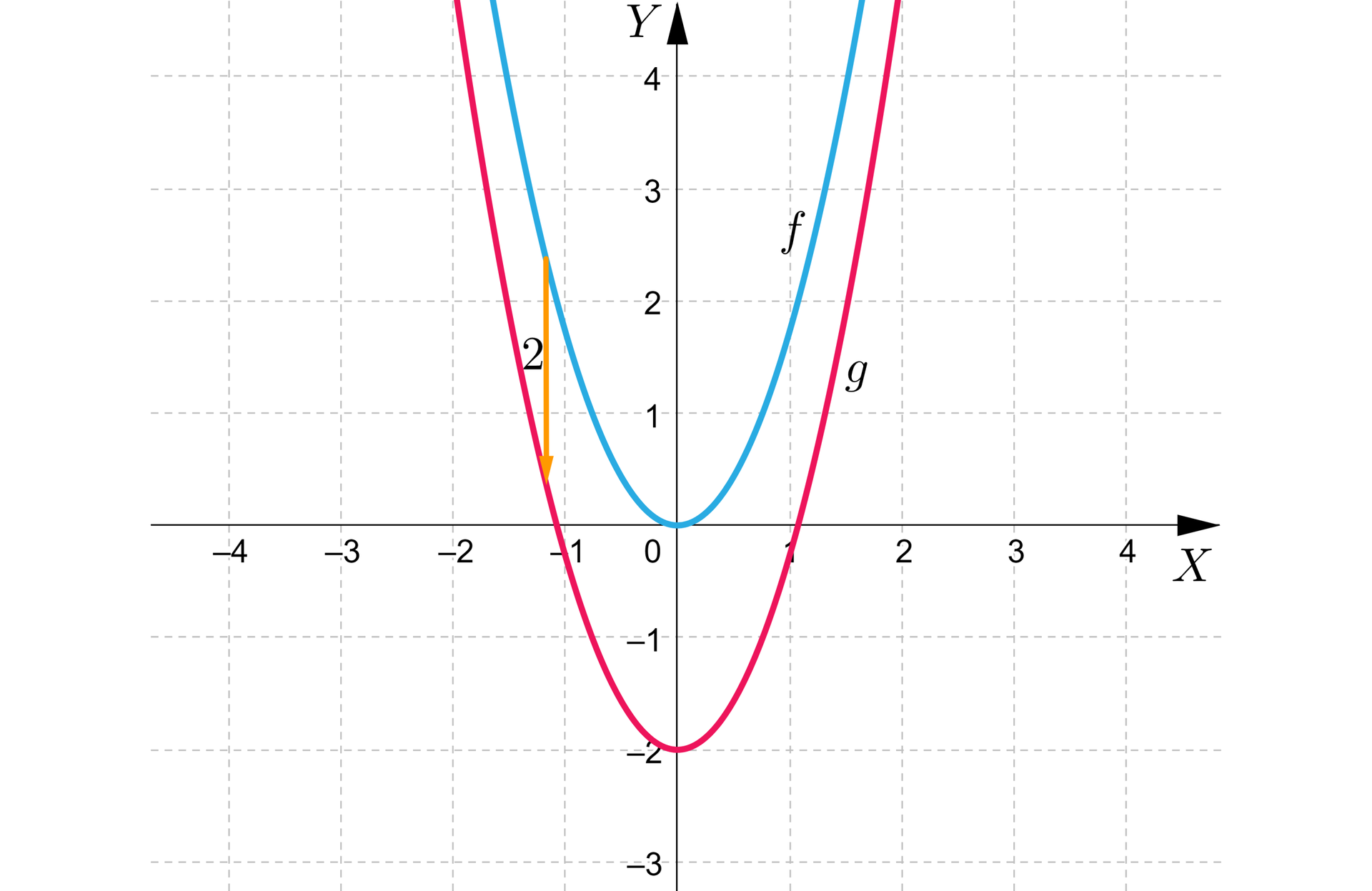
Sporządźmy wykres funkcji określonej wzorem $f (x) = - \frac{1}{3} x^{2}$ .

W celu naszkicowania paraboli, będącej wykresem funkcji przedstawmy w tabeli wartości funkcji $f$ dla kilku argumentów:

$x$	$- 3$	$- 1$	$0$	$1$	$3$
$f (x)$	$- 3$	$- \frac{1}{3}$	$0$	$- \frac{1}{3}$	$- 3$

Wykres funkcji $f$ przedstawia się następująco:

RsoMoWTGhV6uM

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od pięciu do pięciu oraz z pionową osią Y od minus pięciu do jeden. W układzie współrzędnych zaznaczono funkcję kwadratową f, której wykres jest parabolą z ramionami skierowanymi do dołu oraz wierzchołkiem w początku układu współrzędnych. Parabola przechodzi przez punkty -3,-3 oraz 3,-3 .

Przesuniemy ten wykres o $1$ jednostkę w górę wzdłuż osi $Y$ .

Wykresy funkcji przedstawiają się następująco:

R1X2Sq1sv2iAy

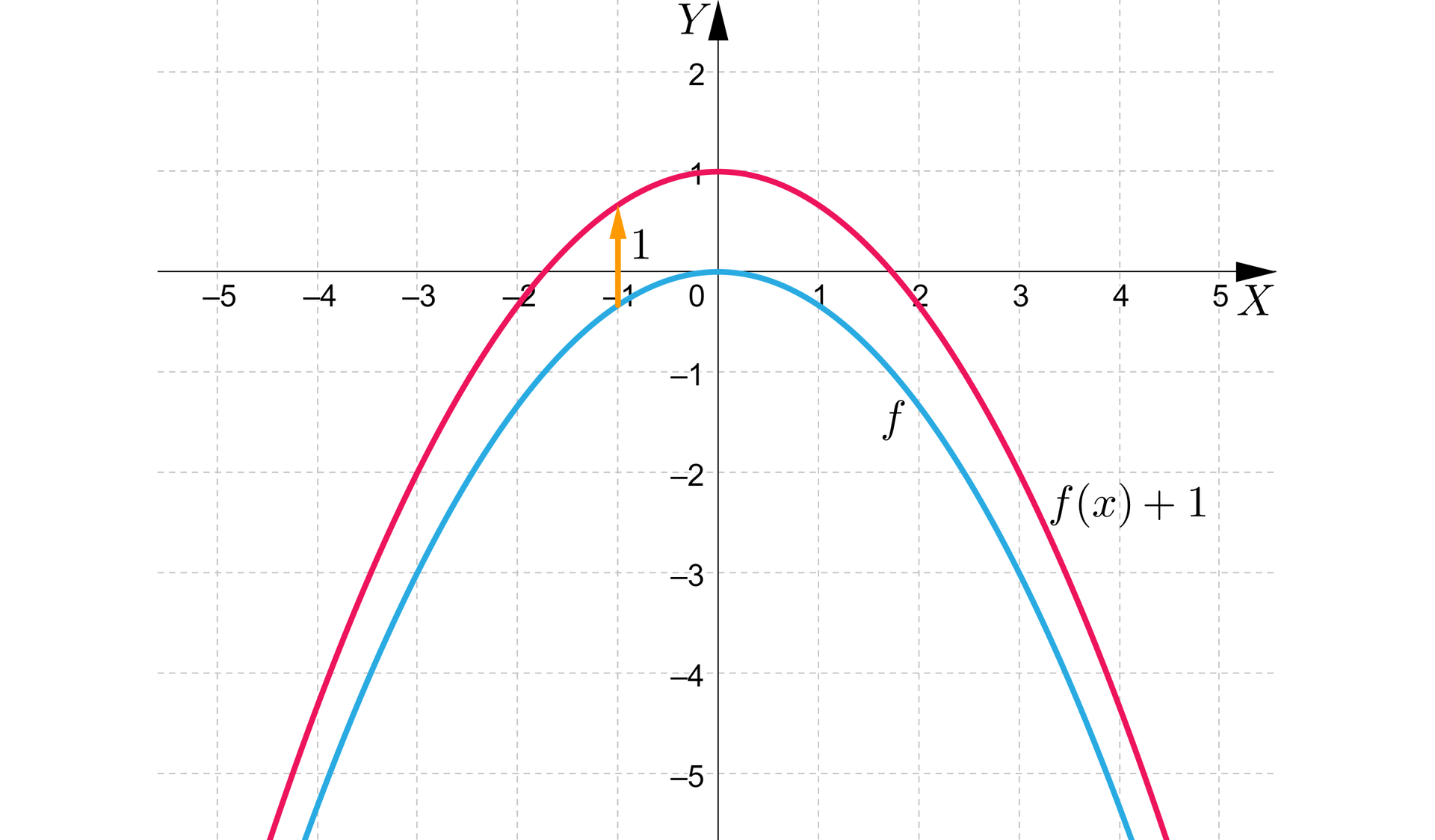
Funkcje f i g(x)=f(x)+1 mają te same dziedziny oraz:

równanie osi symetrii ich wykresów to $x = 0$ ,
przedział, w którym obie funkcje są rosnące to $(- \infty, 0⟩$ ,
przedział, w którymobie funkcje są malejące to $⟨0, \infty)$ .

Zauważmy, że przy przesunięciu wykresu funkcji o $1$ jednostkę w górę wzdłuż osi $Y$ :

zmienił się zbior wartości funkcji z przedziału $(- \infty, 0⟩$ na przedział $(- \infty, 1⟩$ ,
zmieniły się współrzędne wierzchołka paraboli, z punktu o współrzędnych $(0, 0)$ do punktu o współrzędnych $(0, 1)$ ,
zmieniła się wartość największa funkcji, z liczby $0$ na liczbę $1$ dla argumentu $x = 0$ .

Jeżeli przesuwamy parabolę, będącą wykresem funkcji kwadratowej określonej wzorem $f (x) = a x^{2}$ , gdzie $a < 0$ , wzdłuż osi $Y$ o $q$ jednostek w górę lub o $q$ jednostek w dół, otrzymując wykres funkcji g to:

zbiorem wartości funkcji g jest przedział $(- \infty, q⟩$ ,
wierzchołkiem paraboli, która jest wykresem funkcji g, jest punkt o współrzędnych $(0, q)$ ,
funkcja g osiąga wartość największą dla argumentu $x = 0$ wynoszącą $q$ .

W celu otrzymania paraboli, będącej wykresem funkcji kwadratowej określonej wzorem $g (x) = a x^{2} + q$ wystarczy parabolę, będącą wykresem funkcji kwadratowej $f (x) = a x^{2}$ , gdzie $a \in ℝ$ oraz $a \neq 0$ :

przesunąć o $q$ jednostek w górę lub w dół wzdłuż osi $Y$ ,
przesunąć o wektor $\vec{u} = [0, q]$ .

Przykład 1

Dana jest funkcja kwadratowa określona wzorem $f (x) = - \frac{1}{4} x^{2}$ . Parabolę, będącą wykresem funkcji $f$ przesunięto o $3$ jednostki w górę wzdłuż osi $Y$ i otrzymano parabolę, będącą wykresem funkcji $g$ .

R80koVNoHeBDk

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do sześciu oraz z pionową osią Y od minus pięciu do czterech. W układzie współrzędnych zaznaczono funkcję kwadratową f, której wykres jest parabolą z ramionami skierowanymi do dołu oraz wierzchołkiem w początku układu współrzędnych. Parabola przechodzi przez punkty -4,-4 oraz 4,-4 .W tym samym układzie zaznaczono również wykres funkcji g, czyli wykres funkcji f przeniesiony o trzy jednostki do góry, który przechodzi przez punkty -4,-1 oraz 4,-1.

Wyznaczymy:

a) zbiór wartości funkcji $g$ ,

b) współrzędne wierzchołka paraboli, która jest wykresem funkcji $g$ ,

c) wartość największą funkcji $g$ .

Rozwiązanie:

a) zbiorem wartości funkcji $g$ jest przedział $(- \infty, - 3⟩$ ,

b) wierzchołek paraboli, będącej wykresem funkcji $g$ ma współrzędne $(0, 3)$ ,

c) funkcja $g$ osiąga wartość największą równą $3$ dla $x = 0$ .

Przykład 2

Parabolę, będącą wykresem funkcji kwadratowej $f$ określonej wzorem $f (x) = a x^{2}$ , dla $a < 0$ , przesunięto najpierw o $3$ jednostki w dół, a następnie o $7$ jednostek w górę wzdłuż osi $Y$ i otrzymano parabolę, będącą wykresem funkcji $g$

Wyznaczymy:

a) zbiór wartości funcji $g$ ,

b) liczbę rozwiązań równania $g (x) = 4$ .

Rozwiązanie:

Zauważmy, że przesunięcie paraboli, będącej wykresem funkcji $f$ o $3$ jednostki w dół, a następnie o $7$ jednostek w górę wzdłuż osi $Y$ , oznacza przesunięcie tego wykresu o $4$ jednostki w górę wzdłuż osi $Y$ .

Zatem:

a) zbiorem wartości funkcji $g$ jest przedział ( $- \infty, 4 >$ ,

b) wierzchołkiem paraboli, która jest wykresem funkcji $g$ jest punkt o współrzędnych $(0, 4)$ , więc równanie $f (x) = 4$ ma dokładnie jedno rozwiązanie.

Przykład 3

Dana jest funkcja kwadratowa określona wzorem $f (x) = \sqrt{5} x^{2}$ . Parabolę, będącą wykresem tej funkcji przesunięto o $2$ jednostki w dół wzdłuż osi $Y$ i otrzymano parabolę, będącą wykresem funkcji $g$ .

RJhzhwPVUgfvC

Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus czterech do czterech oraz z pionową osią Y od minus trzech do czterech. W układzie współrzędnych zaznaczono funkcję kwadratową f, której wykres jest parabolą z ramionami skierowanymi do góry oraz wierzchołkiem w początku układu współrzędnych. Parabola przechodzi przez punkty -1,5 oraz 1,5 .W tym samym układzie zaznaczono również wykres funkcji g, czyli wykres funkcji f przeniesiony o dwie jednostki do dołu.

Określimy liczbę rozwiązań równania $g (x) = m$ , gdy $m \in ℝ$ .

Rozwiązanie:

Zauważmy, że po przesunięciu paraboli, będącej wykresem funkcji $f$ wierzchołek otrzymanej paraboli, będącej wykresem funkcji $g$ ma współrzędne $(0, - 2)$ .

Ponieważ $a = \sqrt{5} > 0$ , zatem ramiona paraboli, będącej wykresem funkcji $g$ są skierowane do góry.

Zatem równanie $g (x) = m$ , gdy $m \in ℝ$ :

nie ma rozwiązania, gdy $m \in (- \infty, - 2)$ ,
ma jedno rozwiązanie, gdy $m = - 2$ ,
ma dwa rozwiązania, gdy $m \in (- 2, \infty)$ .

Przykład 4

Na rysunku przedstawiono parabolę, będącą wykresem funkcji kwadratowej $f (x)$ .

R1CGWJVJQUk9J

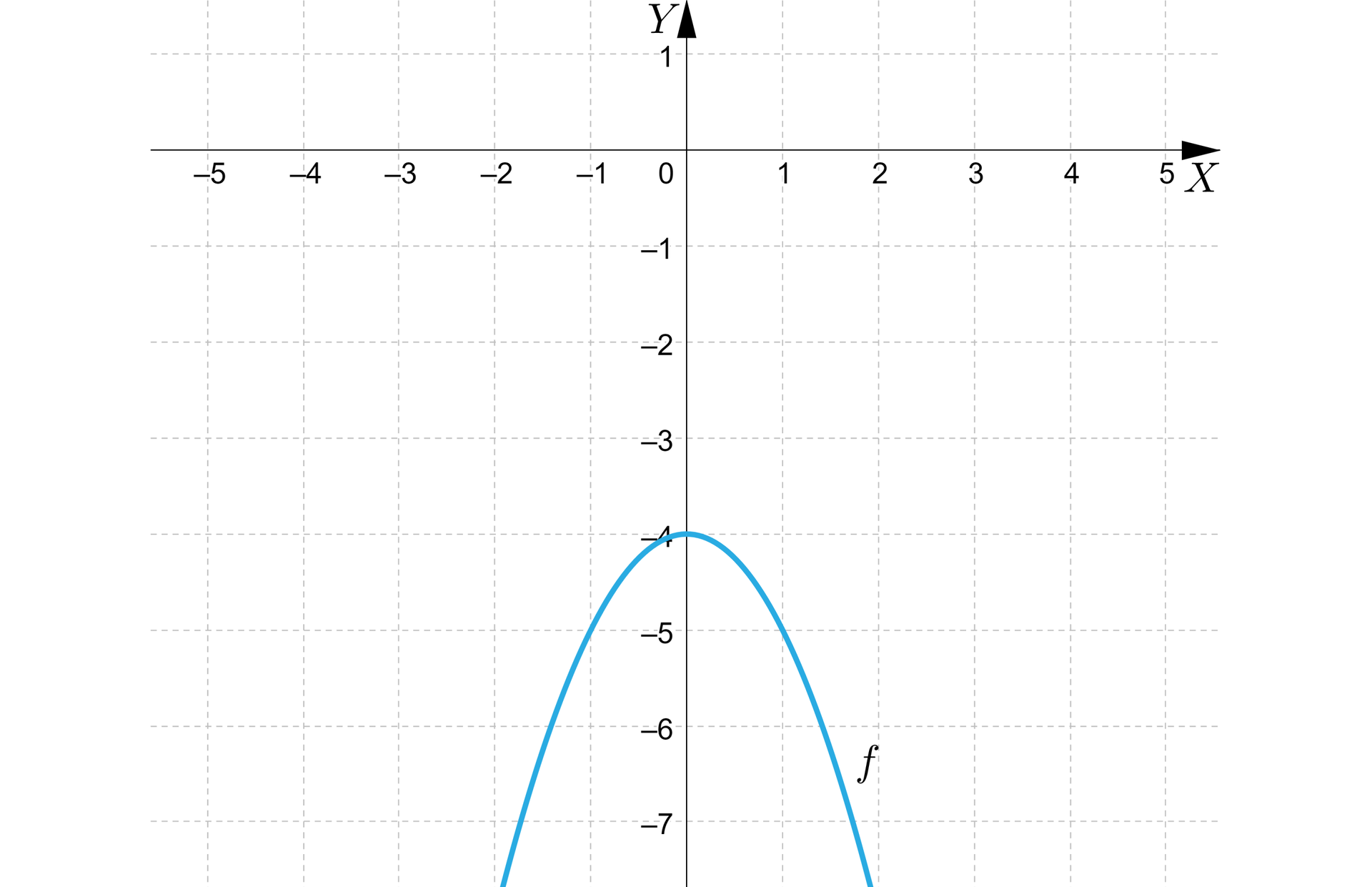
Na ilustracji przedstawiono układ współrzędnych z poziomą osią X od minus pięciu do pięciu oraz z pionową osią Y od minus siedmiu do jeden. W układzie współrzędnych zaznaczono funkcję kwadratową f, której wykres jest parabolą z ramionami skierowanymi do dołu oraz z wierzchołkiem w punkcie 0,-4. Parabola przechodzi przez punkty -1,-5/mn> oraz 1,-5 .

Na podstawie wykresu:

a) odczytamy współrzędne wierzchołka tej paraboli,

b) rozwiążemy nierówność $m - 1 < k$ , gdzie $k$ oznacza liczbę rozwiązań równania $f (x) = - 5$ .

Rozwiązanie:

a) z wykresu odczytujemy, że współrzędne wierzchołka paraboli wynoszą $(0, - 4)$ ,

b) równanie $f (x) = - 5$ ma dwa rozwiązania,

zatem:

$m - 1 < 2$ , więc $m < 3$ .

Przykład 5

Wykażemy, że jeśli funkcja kwadratowa $f$ jest określona wzorem $f (x) = a x^{2} + q$ , gdzie $a > 0$ oraz $q < 0$ , to różnica miejsc zerowych (od większej liczby odejmujemy mniejszą) funkcji $f$ wynosi $\frac{2 \sqrt{- a q}}{a}$ .

Rozwiązanie:

Obliczamy miejsca zerowe funkcji $f$ :

$f (x) = 0 \Leftrightarrow a x^{2} + q = 0$

$a x^{2} = - q$ , czyli $x = \sqrt{\frac{- q}{a}} = \frac{\sqrt{- a q}}{a}$ lub $x = - \sqrt{\frac{- q}{a}} = - \frac{\sqrt{- a q}}{a}$

Zatem różnica miejsc zerowych funkcji $f$ wynosi:

$\frac{\sqrt{- a q}}{a} - (- \frac{\sqrt{- a q}}{a}) = \frac{2 \sqrt{- a q}}{a}$

Przykład 6

Wykażemy, że funkcja $f$ określona wzorem $f (x) = a x^{2} + q$ dla $a < 0$ jest malejąca w przedziale $⟨ 0, \infty)$ .

Rozwiązanie:

Załóżmy, że $x_{1}, x_{2} \in D_{f}$ oraz $x_{1} < x_{2}$ .

Wówczas:

$f (x_{2}) - f (x_{1}) = a \cdot {x_{2}}^{2} + q - (a \cdot {x_{1}}^{2} + q) = a \cdot {x_{2}}^{2} + q - a \cdot {x_{1}}^{2} - q =$

$= a \cdot ({x_{2}}^{2} - {x_{1}}^{2})$

Zauważmy, że $a \cdot ({x_{2}}^{2} - {x_{1}}^{2}) < 0$ , bo $a < 0$ oraz ${x_{2}}^{2} - {x_{1}}^{2} > 0$ .

Wobec tego $f (x_{2}) - f (x_{1}) < 0$ , czyli $f (x_{1}) > f (x_{2})$ .

Stąd wnioskujemy, że funkcja $f$ jest malejąca w przedziale $⟨ 0, \infty)$ .

Słownik

przekształcenie wykresu funkcji:

f (x) + q

przekształcenie wykresu funkcji:

f (x) + q

przesunięcie wykresu funkcji $f$ wzdłuż osi $Y$ o $q$ jednostek w górę ( $q > 0$ ) lub o $q$ jednostek w dół ( $q < 0$ )

Wprowadzenie

Symulacja interaktywna

Słownik