Symulacja interaktywna
Polecenie 1
Uruchom symulację interaktywną, a następnie odczytaj współrzędne wierzchołka paraboli, będącej wykresem funkcji kwadratowej, zbiór wartości oraz oraz wartość najmniejszą lub największą po przesunięciu wykresu funkcji kwadratowej określonej wzorem wzdłuż osi .
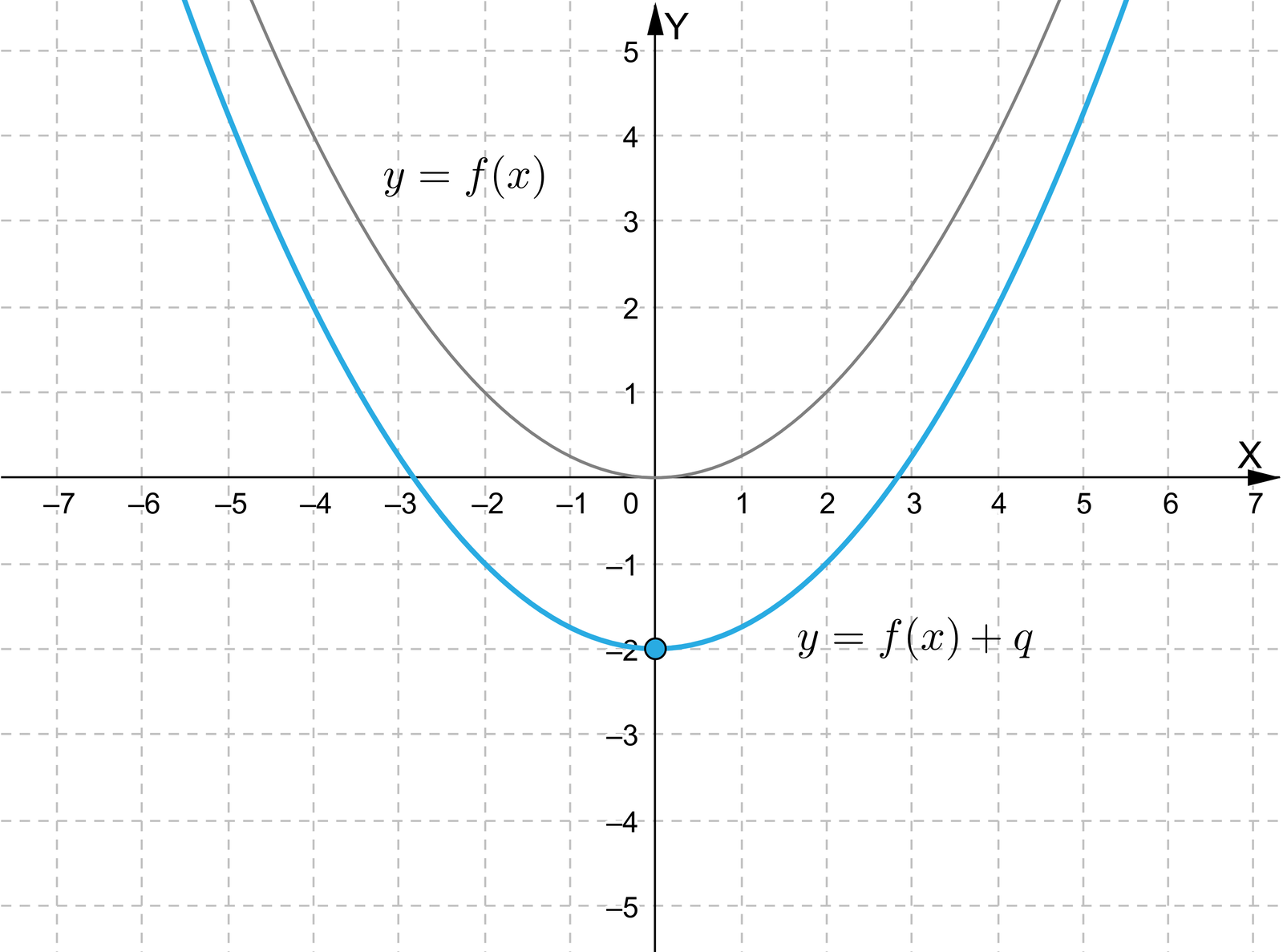
Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/DzGeSrJfv
Polecenie 2
Dana jest funkcja kwadratowa określona wzorem . Parabolę, będącą wykresem funkcji przesunięto wzdłuż osi i otrzymano wykres funkcji . Podaj współrzędne wierzchołka paraboli, będącej wykresem funkcji , zbiór wartości oraz wartość najmniejszą lub największą funkcji, jeżeli parabolę, będącą wykresem funkcji przesunięto:
a) o jednostki w dół,
b) o jednostki w górę