Wyznaczymy wartość najmniejszą oraz wartość największą funkcji kwadratowej $f$ określonej wzorem $f\left(x\right)=x^2-2x-3$.

Rozwiązanie:

Ponieważ $a>0$, wykresem funkcji $f$ jest parabola o ramionach skierowanych w górę, a funkcja przyjmuje wartość najmniejszą w wierzchołku paraboli. Funkcja $f$ nie przyjmuje tym samym wartości największej.

Pierwszą współrzędną wierzchołka $W=\left(p,q\right)$ tej paraboli wyznaczymy korzystając ze wzoru:

$p=-\frac{b}{2a}$, zatem $p=-\frac{-2}{2·1}=1$.

Najmniejszą wartość funkcji $f$ możemy obliczyć ze wzoru na $q=-\frac{∆}{4a}$ lub przez obliczenie wartości funkcji $f$ dla argumentu $p$.

Wybierając drugi sposób otrzymujemy:

$f\left(1\right)=1^2-2·1-3=-4$.

Zatem wartością najmniejszą funkcji $f$ jest liczba $-4$.

Wyznaczymy wartość najmniejszą i wartość największą w każdym z przedziałów: $⟨-2,0⟩$, $⟨-1,2⟩$, $⟨2,4⟩$ funkcji kwadratowej $f$ określonej wzorem $f\left(x\right)=x^2-2x-3$.

Rozwiązanie:

Zanim wyznaczymy wartość najmniejszą i wartość największą funkcji $f$, naszkicujemy wykres tej funkcji.

Do naszkicowania wykresu funkcji $f$, poza współrzędnymi wierzchołka paraboli, będącej wykresem tej funkcji, wyznaczymy miejsca zerowe funkcji.

W tym celu obliczamy najpierw wartość wyróżnika odpowiedniego trójmianu kwadratowego:

$∆={\left(-2\right)}^2-4·1·\left(-3\right)=16$.

Wykorzystując wzory na miejsca zerowe funkcji kwadratowej $f$, otrzymujemy:

$x_1=\frac{2-4}{2}=-1$,

$x_1=\frac{2+4}{2}=3$.

Miejscami zerowymi funkcji $f$ są liczby $\left(-1\right)$ oraz $3$.

Wykres funkcji $f$ przedstawia się następująco:

R1eylxsD07Dqr

Na ilustracji przedstawiono układ współrzędnych z poziomą osią $X$ od minus pięciu do pięciu, oraz z pionową osią $Y$ od minus czterech do czterech. Na płaszczyźnie narysowano parabolę, której wierzchołek znajduje się w punkcie o współrzędnych $\left(1;-4\right)$, a ramiona skierowane są w górę. Wykres funkcji przecina oś $X$ w punkcie x, równa się, minus jeden, oraz x, równa się, trzy. Po lewo napisano wzór funkcji $f\left(x\right)=x^2-2x-3$.

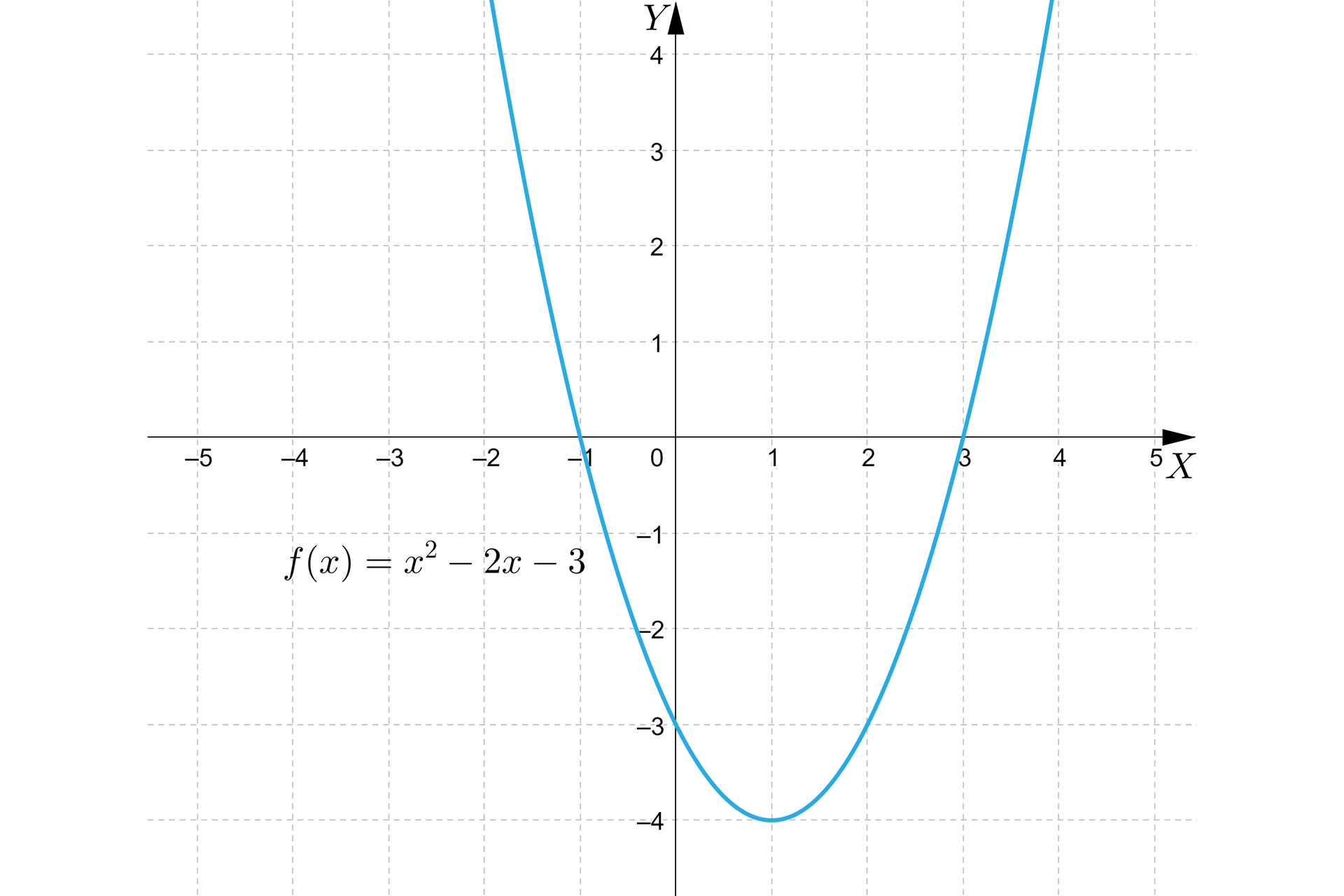
Wyznaczamy wartość najmniejszą oraz wartość największą funkcji $f$ w przedziałach:

• $⟨-2,0⟩$

Ponieważ $p=1\notin ⟨-2,0⟩$, zatem wystarczy obliczyć wartości funkcji $f$ na końcach tego przedziału.

Wobec tego: $f\left(-2\right)={\left(-2\right)}^2-2·\left(-2\right)-3=5$, $f\left(0\right)=0^2-2·0-3=-3$.

Ponieważ $-3<5$, zatem wartość najmniejsza funkcji $f$ w przedziale $⟨-2,0⟩$ wynosi $\left(-3\right)$, a wartość największa $f$ wynosi $5$.

• $⟨-1,2⟩$

Ponieważ $p=1\in ⟨-1,2⟩$, zatem funkcja $f$ przyjmuje wartość najmniejszą dla $x=1$, a wartość największą w jednym z końców podanego przedziału.

Wobec tego: $f\left(-1\right)={\left(-1\right)}^2-2·\left(-1\right)-3=0$, $f\left(1\right)=-4$, $f\left(2\right)=2^2-2·2-3=-3$.

Ponieważ $-3<0$, to wartość najmniejsza funkcji $f$ w przedziale $⟨-1,2⟩$ wynosi $\left(-4\right)$, a wartość największa funkcji $f$ wynosi $0$.

• $⟨2,4⟩$

Ponieważ $p=1\notin ⟨2,4⟩$, zatem wystarczy obliczyć wartości funkcji $f$ na końcach tego przedziału.

Wobec tego: $f\left(2\right)=2^2-2·2-3=-3$, $f\left(4\right)=4^2-2·4-3=5$.

Ponieważ $-3<5$, to wartość najmniejsza funkcji $f$ w przedziale $⟨2,4⟩$ wynosi $\left(-3\right)$ , a wartość największa funkcji $f$ wynosi $5$.

Wyznaczymy wartość najmniejszą i wartość największą w przedziale $⟨-2,1⟩$ funkcji kwadratowej $f$ określonej wzorem $f\left(x\right)=-2x^2+x+6$. .

Rozwiązanie:

Ponieważ $a=-2<0$, zatem funkcja kwadratowa $f$ przyjmuje wartość największą w wierzchołku paraboli, która jest wykresem tej funkcji.

Sprawdźmy, czy wartość pierwszej współrzędnej wierzchołka $p$ paraboli, będącej wykresem funkcji kwadratowej $f$ należy do przedziału $⟨-2,1⟩$.

Obliczamy $p=\frac{-1}{2·\left(-2\right)}=\frac{1}{4}$.

Ponieważ $p=\frac{1}{4}\in ⟨-2,1⟩$, zatem funkcja kwadratowa $f$ przyjmuje wartość największą w wierzchołku, a wartość najmniejszą w jednym z końców przedziału $⟨-2,1⟩$.

Zatem:

$f\left(-2\right)=-2·{\left(-2\right)}^2-2+6=-4$,

$f\left(\frac{1}{4}\right)=-2·{\left(\frac{1}{4}\right)}^2+\frac{1}{4}+6=6\frac{1}{8}$,

$f\left(1\right)=-2·1^2+1+6=5$.

Wobec tego, że $-4<6\frac{1}{8}$, to wartość najmniejsza funkcji $f$ w przedziale $⟨-2,1⟩$ wynosi $\left(-4\right)$, a wartość największa funkcji $f$ wynosi $6\frac{1}{8}$.

Funkcja $f$ określona w przedziale $⟨-2,2⟩$ przyporządkowuje każdej liczbie z tego przedziału jej kwadrat pomniejszony o połowę tej liczby. Wyznaczymy zbiór wartości tej funkcji.

Rozwiązanie:

Funkcję z zadania zapisujemy za pomocą wzoru $f\left(x\right)=x^2-\frac{1}{2}x$, gdzie .

Wyznaczenie zbioru wartości funkcji $f$ sprowadza się do znalezienia wartości najmniejszej i największej tej funkcji w przedziale $⟨-2,2⟩$.

Obliczamy pierwszą współrzędną wierzchołka paraboli, na której leży  wykres funkcji $f$:

$p=\frac{{\displaystyle \frac{1}{2}}}{2}=\frac{1}{4}$.

Ponieważ $p=\frac{1}{4}\in ⟨-2,2⟩$, zatem wykorzystując przedstawioną wcześniej metodę, obliczamy wartości funkcji $f$ w trzech punktach:

$f\left(-2\right)={\left(-2\right)}^2-\frac{1}{2}·\left(-2\right)=5$,

$f\left(\frac{1}{4}\right)={\left(\frac{1}{4}\right)}^2-\frac{1}{2}·\left(\frac{1}{4}\right)=-\frac{1}{16}$,

$f\left(2\right)=2^2-\frac{1}{2}·2=3$.

Ponieważ $-\frac{1}{16}<5$, to najmniejsza wartość funkcji $f$ w przedziale $⟨-2,2⟩$ jest równa $\left(-\frac{1}{16}\right)$, a wartość największa funkcji $f$ wynosi $5$.

Zbiorem wartości funkcji $f$ jest przedział $⟨-\frac{1}{16},5⟩$.

Wyznaczymy najmniejszą wartość oraz największą wartość w przedziale $⟨0,4⟩$ funkcji $f$ określonej wzorem $f\left(x\right)=\frac{1}{x^2-4x+8}$.

Rozwiązanie:

Rozpatrzmy pomocniczo funkcję $g$ określoną wzorem $g\left(x\right)=x^2-4x+8$.

Wyznaczymy wartość najmniejszą oraz wartość największą funkcji $g$ w przedziale $⟨0,4⟩$.

Obliczamy pierwszą współrzędną $p$ wierzchołka paraboli, będącej wykresem funkcji $g$:

$p=\frac{4}{2}=2$

Ponieważ $p=2\in ⟨0,4⟩$, zatem funkcja $g$ przyjmuje wartość najmniejszą w wierzchołku paraboli, będącej wykresem tej funkcji, a wartość największą w danym przedziale  w jednym z końców przedziału $⟨0,4⟩$.

Zatem:

$g\left(0\right)=0^2-4·0+8=8$

$g\left(2\right)=2^2-4·2+8=4$

$g\left(4\right)=4^2-4·4+8=8$

Ponieważ $4<8$, to wartość najmniejsza funkcji $g$ w przedziale $⟨0,4⟩$ wynosi $4$, a wartość największa funkcji wynosi $8$.

Zauważmy, że zachodzi zależność: $f\left(x\right)=\frac{1}{g\left(x\right)}$ i funkcja g w rozpatrywanym przedziale przyjmuje tylko wartości dodatnie.

Wobec tego wartość najmniejsza funkcji $f$ w przedziale $⟨0,4⟩$ wynosi:

$f\left(0\right)=f\left(4\right)=\frac{1}{g\left(4\right)}=\frac{1}{8}$

a wartość największa funkcji $f$ w przedziale $⟨0,4⟩$ wynosi $f\left(2\right)=\frac{1}{g\left(2\right)}=\frac{1}{4}$

Wyznaczymy wartość najmniejszą oraz wartość największą w przedziale $⟨2,3⟩$ funkcji $f$ określonej wzorem $f\left(x\right)=\sqrt{-x^2+5x-6}$.

Rozwiązanie:

Rozpatrzmy pomocniczo funkcję $g$ określoną wzorem $g\left(x\right)=-x^2+5x-6$.

Wyznaczymy wartość najmniejszą oraz wartość największą funkcji $g$ w przedziale $⟨2,3⟩$.

Obliczamy pierwszą współrzędną $p$ wierzchołka paraboli, będącej wykresem funkcji $g$:

$p=\frac{-5}{-2}=\frac{5}{2}$

Ponieważ $p=\frac{5}{2}\in ⟨2,3⟩$, zatem funkcja $g$ przyjmuje wartość największą w wierzchołku paraboli, będącej wykresem tej funkcji, a wartość najmniejszą w jednym z końców przedziału $⟨2,3⟩$.

Zatem:

$g\left(2\right)=-2^2+5·2-6=0$

$g(\frac{5}{2})=-{\left(\frac{5}{2}\right)}^2+5\cdot \frac{5}{2}-6=\frac{1}{4}$

$g(3)=-3^2+5\cdot 3-6=0$

Ponieważ $0<\frac{1}{4}$, to wartość najmniejsza funkcji $g$ w przedziale $⟨2,3⟩$ wynosi $0$, a wartość największa funkcji wynosi $\frac{1}{4}$. Wynika stąd również, że w rozpatrywanym przedziale funkcja g przybiera tylko wartości nieujemne.

Zauważmy, że zachodzi zależność: $f\left(x\right)=\sqrt{g\left(x\right)}$.

Wobec tego wartość najmniejsza funkcji $f$ w przedziale $⟨2,3⟩$ wynosi:

$f\left(2\right)=f\left(3\right)=\sqrt{g\left(2\right)}=\sqrt{g\left(3\right)}=0$

a wartość największa funkcji $f$ w przedziale $⟨2,3⟩$ wynosi $f(\frac{5}{2})=\sqrt{g(\frac{5}{2})}=\sqrt{\frac{1}{4}}=\frac{1}{2}$.

funkcja określona na zbiorze $\mathrm{ℝ}$ wzorem $f\left(x\right)=a{x}^2+bx+c$, gdzie $a,b,c\in \mathrm{ℝ}$ oraz $a\ne 0$