Przeczytaj
Poniższy aplet przedstawia rodzaje odcinków w ostrosłupie czworokątnymostrosłupie czworokątnym.
Włączając kolejne kąty i odcinki, dowiesz się, jak nazywają się poszczególne odcinki w ostrosłupie oraz poznasz kąty w ostrosłupie.

Zasób interaktywny dostępny pod adresem https://zpe.gov.pl/a/D1Az9RHI1
Podstawą ostrosłupa jest kwadrat . Krawędź boczna jest wysokością ostrosłupa a jej długość jest trzy razy większa od długości krawędzi podstawy. Obliczymy cosinus kąta między ścianami bocznymi i tego ostrosłupa.
Rozwiązanie:
Niech – długość krawędzi podstawy.
Wykonajmy rysunek pomocniczy.
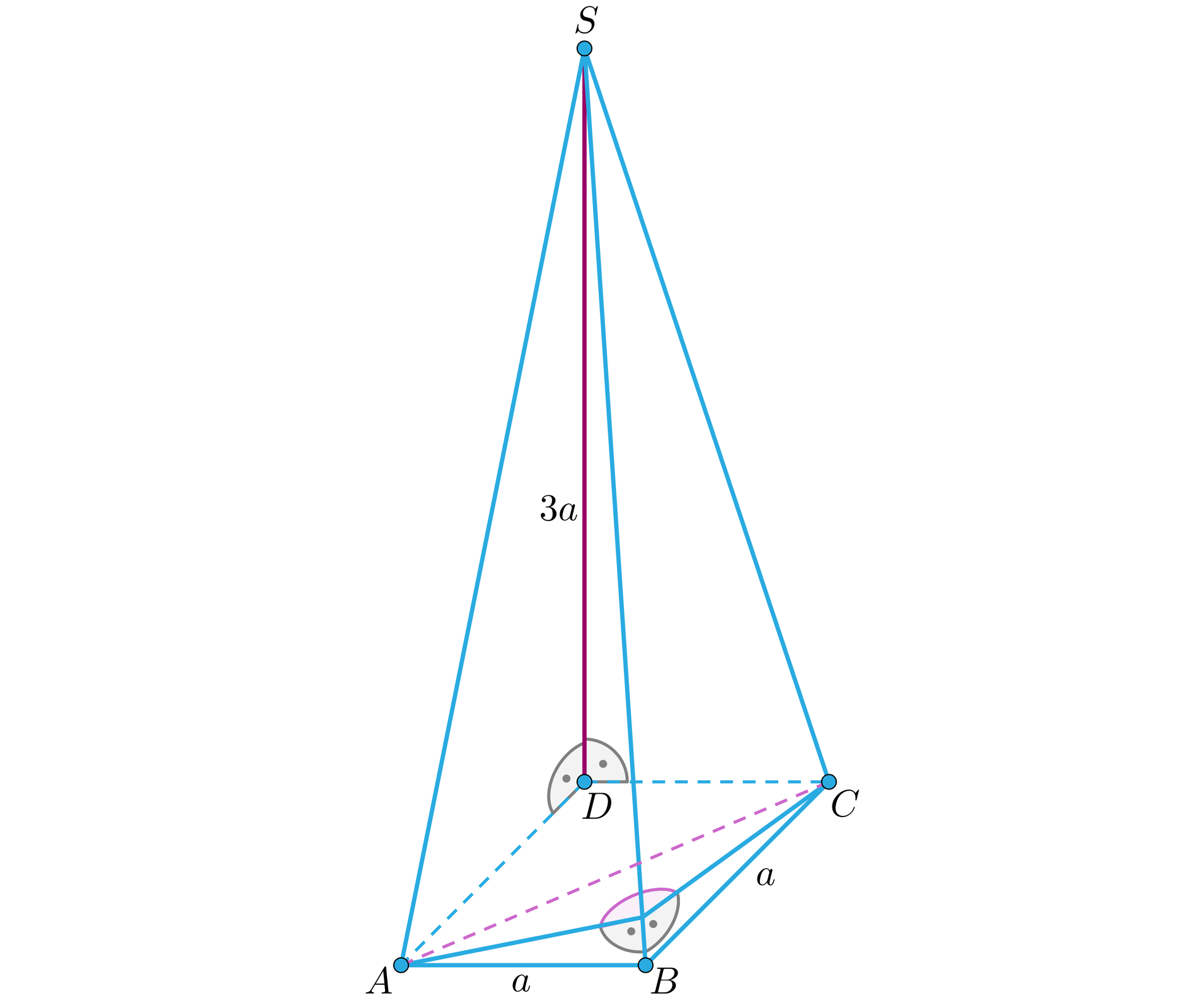
Trójkąty i są prostokątne, więc długości krawędzi i możemy policzyć, wykorzystując twierdzenie Pitagorasa:
.
Analogicznie .
Zauważmy, że trójkąt także jest prostokątny (zapoznaj się z poniższym rysunkiem). Możemy więc obliczyć długość krawędzi .
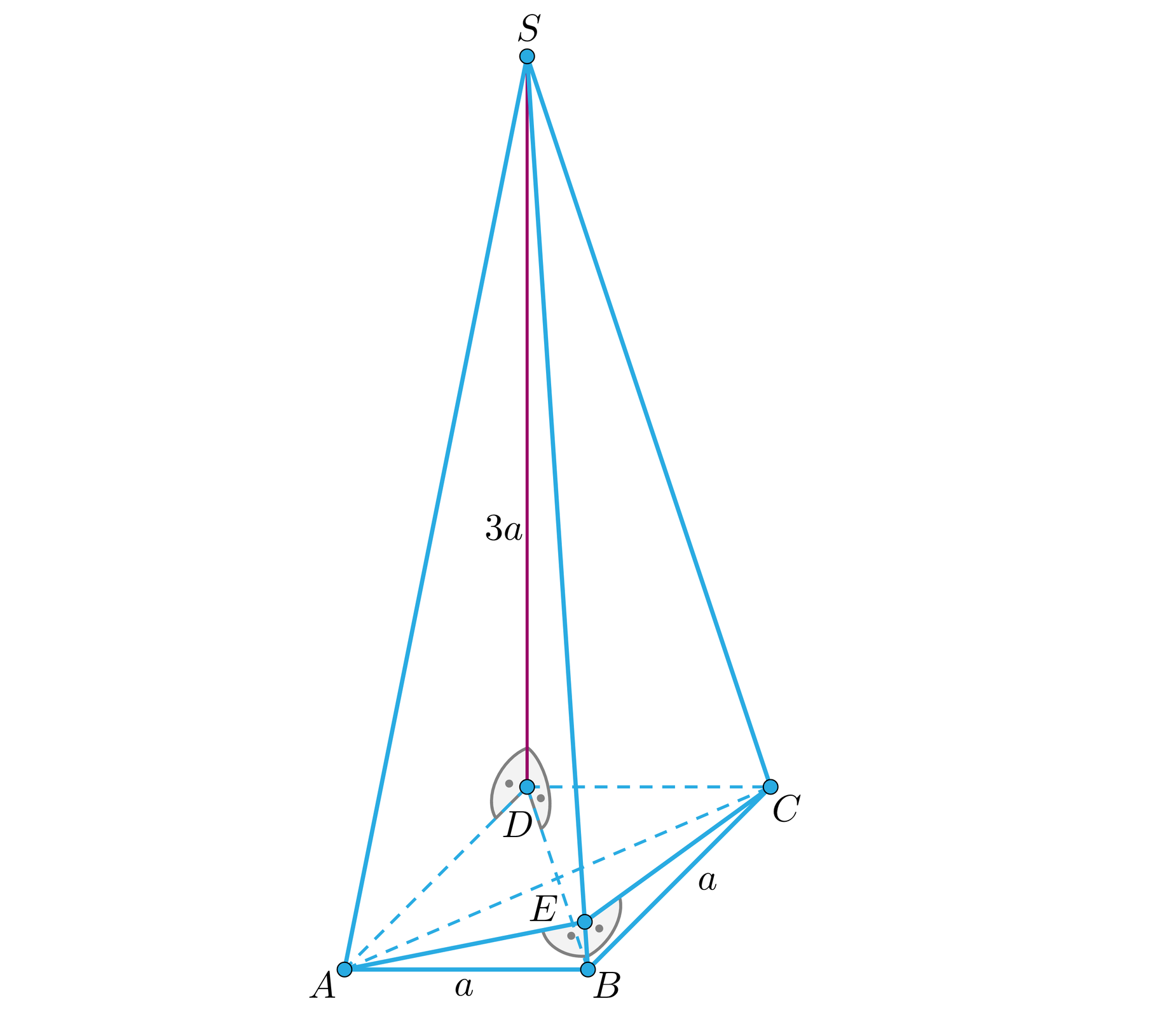
Zauważmy, że trójkąty i są przystającymi trójkątami prostokątnymi, ponieważ:
ich boki są tej samej długości.
na mocy twierdzenia odwrotnego do twierdzenia Pitagorasa w trójkącie mamy:
na mocy twierdzenia odwrotnego do twierdzenia Pitagorasa w trójkącie mamy:
.
Aby obliczyć cosinus kąta między ścianami bocznymi i tego ostrosłupa, musimy znać długości odcinków i . Są to wysokości trójkątów prostokątnych, wychodzące z wierzchołków kątów prostych trójkątów i . Obliczmy pole każdego z trójkątów na dwa sposoby.
Dla trójkąta mamy:
.
Analogicznie:
.
Trójkąt jest równoramienny. Oznaczmy , , więc na mocy twierdzenia cosinusów mamy:
.
Cosinus kąta między ścianami bocznymi i tego ostrosłupa wynosi więc .
Podstawą ostrosłupa jest romb o boku długości . Jeden z kątów rombu ma miarę , i . Obliczymy sinus kąta nachylenia krawędzi do płaszczyzny podstawy ostrosłupa.
Rozwiązanie:
Przypadek
Załóżmy, że kąt rozwarty rombu jest przy wierzchołku .
Narysujemy nasz ostrosłup. Oznaczmy wysokość ostrosłupa jako . Kąt nachylenia krawędzi bocznej do płaszczyzny podstawy oznaczmy jako .

Zauważmy, że do obliczenia sinusa kąta potrzebujemy długości odcinka i długości wysokości . Aby wyznaczyć , obliczymy długość przekątnej .
Zacznijmy od narysowania samej podstawy naszego ostrosłupa i wyznaczenia .
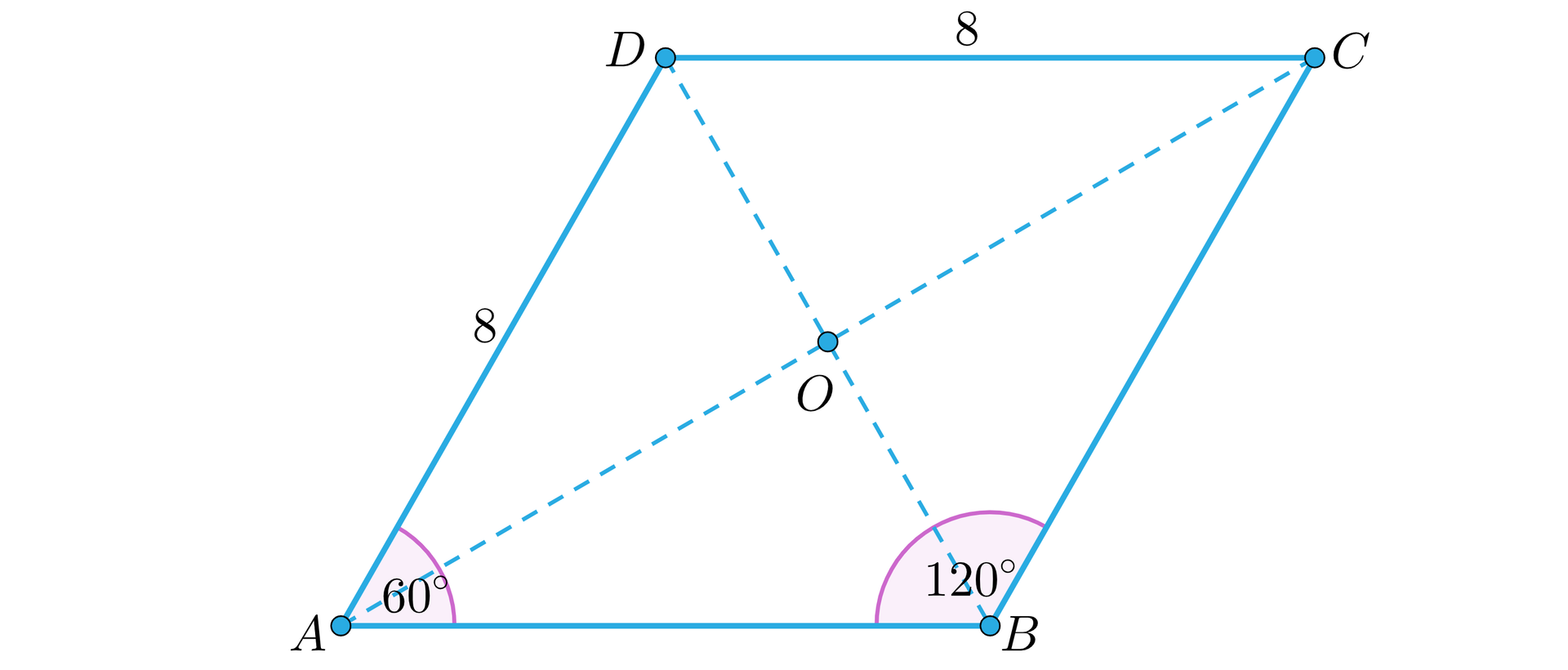
Kąt rozwarty rombu ma miarę , więc kąt ostry .
Zauważmy, że trójkąt jest równoboczny, więc .
Wyznaczymy teraz . Wykorzystamy twierdzenie cosinusów w trójkącie :
.
Wykorzystamy wzory redukcyjne:
.
Obliczymy wysokość ostrosłupa. Wykorzystamy do tego trójkąt , który jest prostokątny. Korzystamy z twierdzenia Pitagorasa. Zauważmy, że .
.
Aby obliczyć sinus kąta nachylenia krawędzi do płaszczyzny podstawy ostrosłupa, musimy znać długość tej krawędzi. Wykorzystajmy trójkąt prostokątny :
.
Wiemy, że . Zatem
.
Obliczmy sinus kąta :
.
Przypadek
Załóżmy teraz, że przy wierzchołku jest kąt ostry. Wykonamy rysunek ostrosłupa i wprowadzimy oznaczenia.
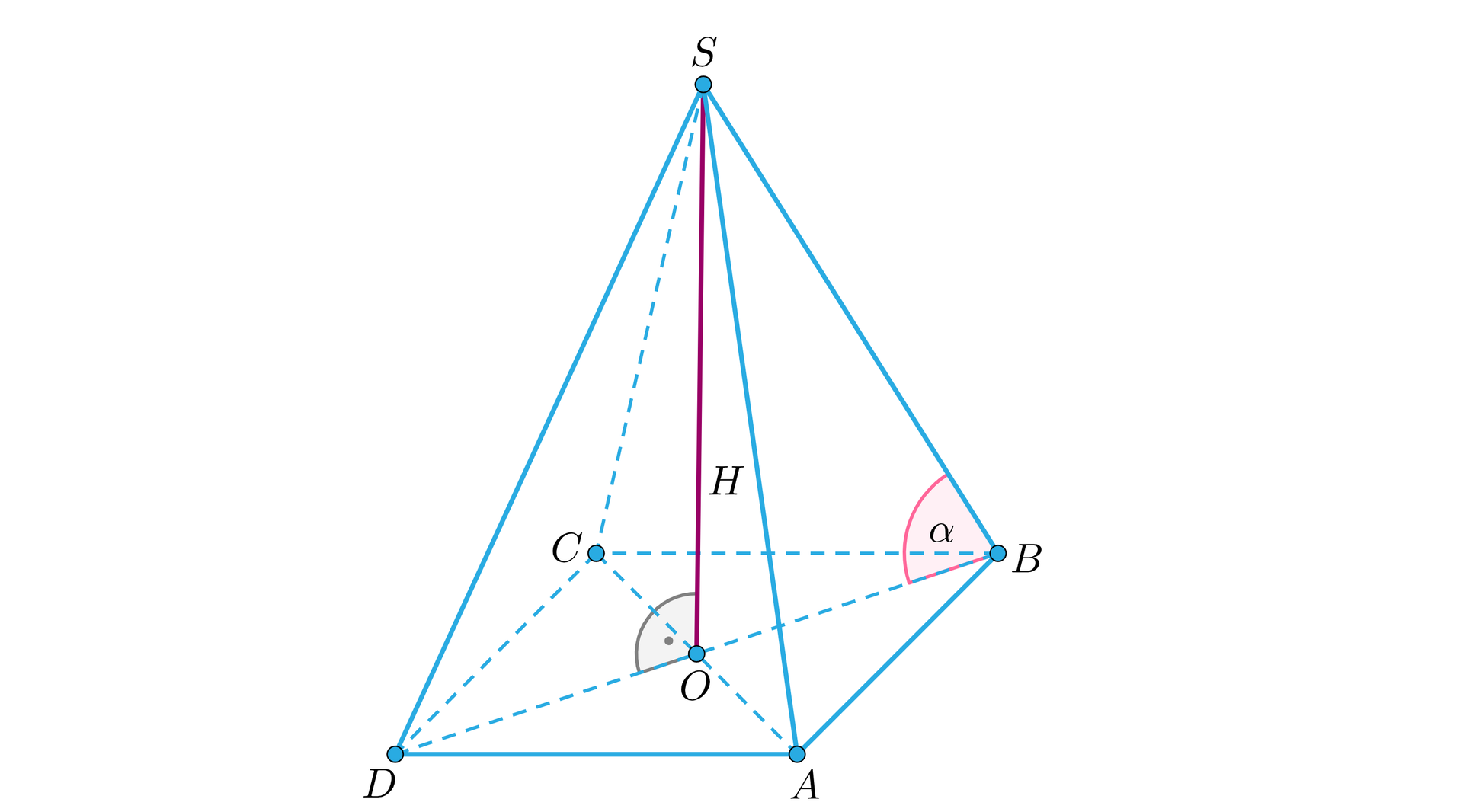
Wtedy .
Zauważmy, że .
Wyznaczymy korzystając z trójkąta prostokątnego :
Wyznaczymy teraz korzystając z trójkąta prostokątnego :
Oczywiście , zatem:
Ostatecznie:
Jedna z krawędzi bocznych ostrosłupa, którego podstawą jest prostokąt, ma długość i jest prostopadła do płaszczyzny podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt o mierze , a jedną z sąsiednich krawędzi bocznych kąt o mierze . Wyznaczymy pole podstawy tego ostrosłupa.
Rozwiązanie:
Wykonamy rysunek pomocniczy. Wprowadzimy dodatkowe oznaczenia:
i – długości boków prostokąta.

Oczywiście trójkąty , i są prostokątne. Z twierdzenia o trzech prostych prostopadłych trójkąt jest również prostokątny a kąt prosty.
Wiemy, że , co daje, że:
.
Skoro trójkąt jest prostokątny, to możemy ułożyć równanie:
.
Obliczmy teraz drugi bok prostokąta, czyli . Z równania mamy:
.
Mając długości boków prostokąta, możemy policzyć jego pole:
.
Podstawą ostrosłupa prostegoostrosłupa prostego jest trapez równoramienny o kącie ostrym , w którym ramię i krótsza podstawa mają długość . Każda krawędź boczna ostrosłupa tworzy z płaszczyzną podstawy kąt . Obliczymy długość promienia okręgu opisanego na trapezie i wysokość ostrosłupa.
Rozwiązanie:
Zajmijmy się na początek samą podstawą naszego ostrosłupa. Wprowadźmy dodatkowe oznaczenia na wysokość trapezu – i długość odcinka (zapoznaj się z rysunkiem) oznaczmy jako :

Trójkąt jest prostokątny. Zatem wykorzystując funkcje trygonometryczne, mamy:
, czyli
, czyli .
Dolna podstawa trapezu ma więc długość .
Wyznaczamy długość promienia okręgu opisanego na trapezie.

Zauważmy, że promień okręgu opisanego na trapezie pokrywa się z promieniem okręgu opisanym na trójkącie .
Z twierdzenia sinusów mamy równość:
Wyznaczymy długość odcinka . Zauwazmy, że:
oraz
Zatem:
.
Stąd:
.
Narysujmy nasz ostrosłup:
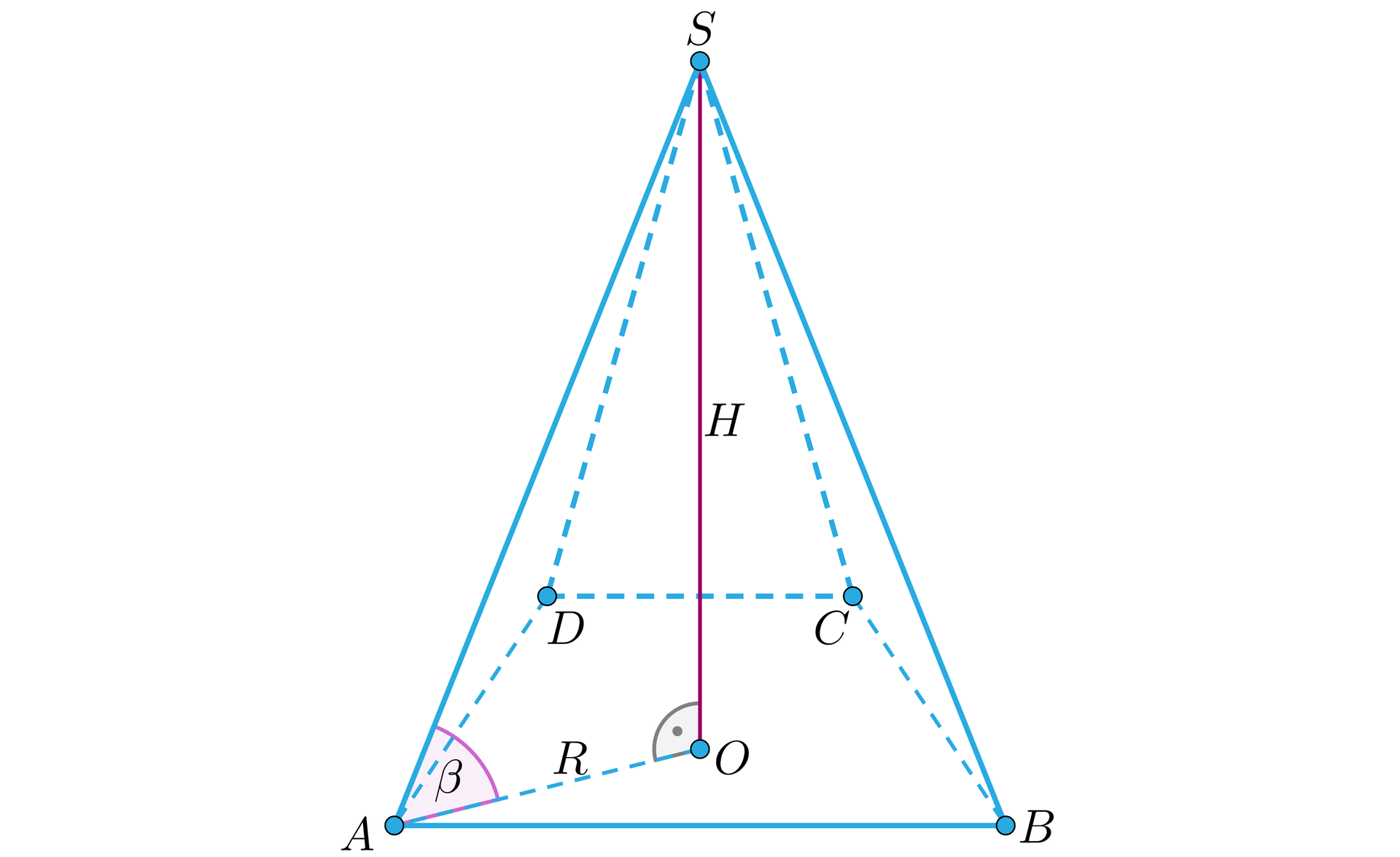
Trójkąt jest prostokątny, więc z funkcji tangens mamy:
.
Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnegoostrosłupa prawidłowego czworokątnego jest równa . Krawędź boczna tworzy z wysokością kąt , taki, że . Obliczmy wysokość ostrosłupa oraz sinus kąta nachylenia krawędzi bocznej do krawędzi podstawy.
Wykonajmy rysunek pomocniczy. Wprowadźmy dodatkowe oznaczenie. Niech – długość krawędzi podstawy, – wysokość ostrosłupa.
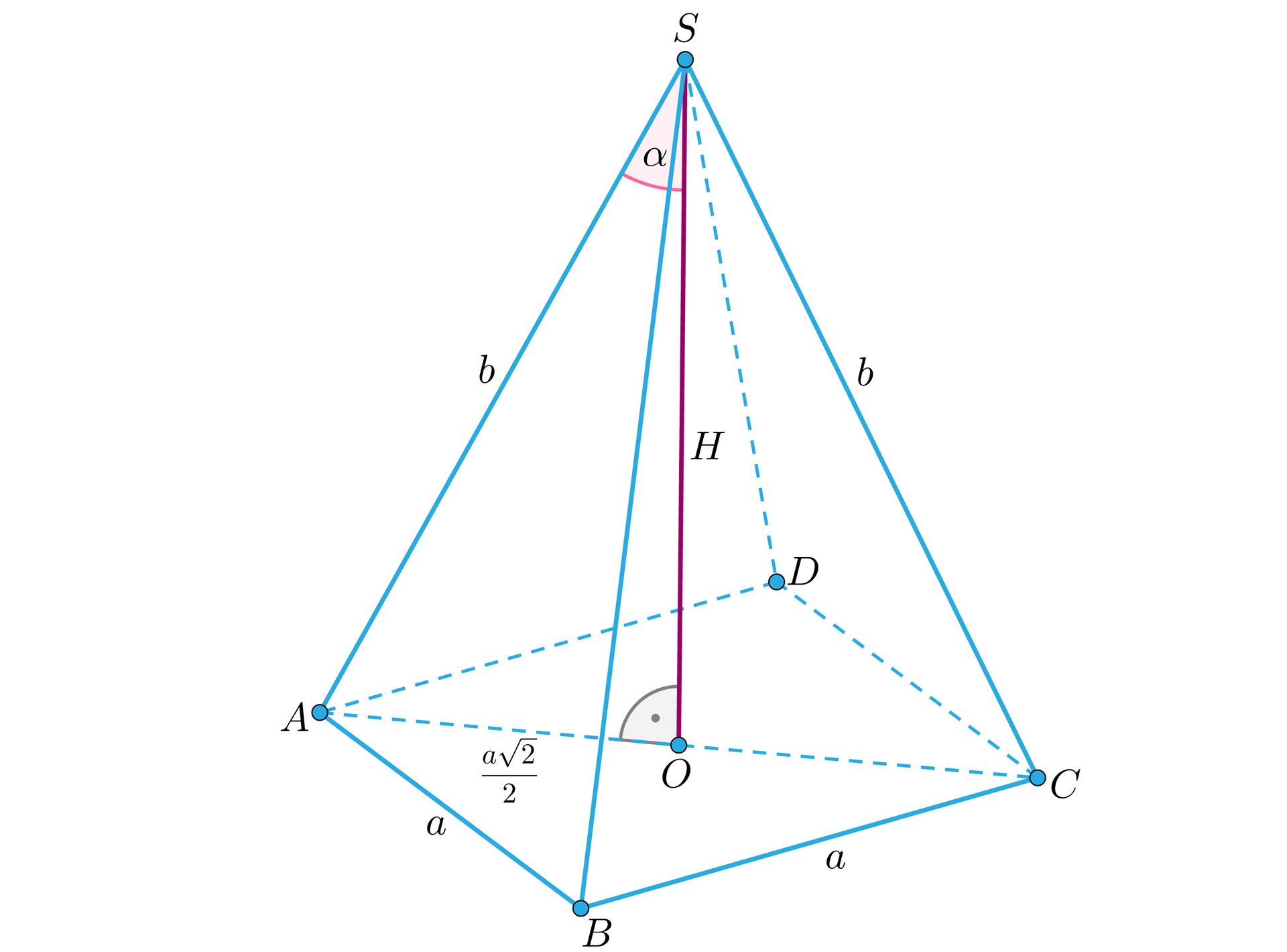
Trójkąt jest prostokątny. Wiemy, że , więc:
.
Ponadto z twierdzenia Pitagorasa mamy:
.
Obliczmy więc wysokość ostrosłupa:
.
Aby obliczyć sinus kąta nachylenia krawędzi bocznej do krawędzi podstawy, narysujmy ten kąt w naszym ostrosłupie. Jego miarę oznaczmy jako .

Trójkąt jest prostokątny, gdyż odcinek jest wysokością trójkąta , czyli ściany bocznej ostrosłupa. Zatem
.
Obliczmy długość odcinka , korzystając z twierdzenia Pitagorasa:
.
Zatem:
.
Słownik
ostrosłup, którego podstawa jest czworokątem a wszystkie krawędzie boczne są tej samej długości; (równoważnie: spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie)
ostrosłup, którego podstawą jest kwadrat a wszystkie krawędzie boczne są tej samej długości, spodek jego wysokości pokrywa się z punktem przecięcia przekątnych kwadratu