Przeczytaj

Na początek proponujemy Ci wykonanie doświadczenia lub symulacji.

RzIrrQv8Vwumh1

Zapoznaj się z przebiegiem doświadczenia. Przeanalizuj uzyskane informacje, a następnie zapoznaj się z poleceniami zamieszczonymi poniżej.

Opis doświadczenia:

Wyrzucamy monety z pojemnika na stół.
Dzielimy monety na dwie grupy: orłów i reszek.
Reszki odkładamy na bok – nie będą już brały udziału w doświadczeniu.
Policzymy orły i wpiszemy odpowiednią liczbę do tabeli.
Monety, na których wypadł orzeł, włożymy do pojemnika i ponownie rozsypmy je na stoliku.
Podzielimy monety na dwie grupy: orłów i reszek.
Reszki odkładamy na bok – nie będą już brały udziału w doświadczeniu. Policzymy orły i wpiszemy odpowiednią liczbę do tabeli.
Kończymy doświadczenie dopiero wtedy, gdy zostanie tylko jedna moneta.

Przeanalizujemy przykład. Postępując zgodnie z instrukcją otrzymujemy tabelę dla sześciu rzutów:

numer rzutu	$1$	$2$	$3$	$4$	$5$	$6$
liczba orłów	$27$	$15$	$9$	$5$	$2$	$1$

Dane zebrane w tabeli można przedstawić w postaci punktów w pierwszej ćwiartce układu współrzędnych, gdzie pierwsza współrzędna określa numer rzutu, a druga liczbę wyrzuconych orłów. Pozioma oś X jest od zera do sześciu, a pionowa oś Y jest od zera do dwudziestu siedmiu. Zaznaczono w nim punkty $(1; 27)$ , $(2; 15)$ , $(3; 9)$ , $(4; 5)$ , $(5; 2)$ oraz $(6; 1)$ . Zostały one połączone linią ciągłą od pierwszego do ostatniego punktu.

Polecenie 1

RKOCi9imfH6up

Zbadaj rozpad promieniotwórczy przy użyciu poniższej symulacji.

W próbce znajduje się $1000$ jąder promieniotwórczych (szarych kółeczek). W chwili uruchomienia symulacji jądra ulegają rozpadowi, czyli przemianie promieniotwórczej (kolor kółeczka zmienia się z szarego na niebieski). Symulację można zatrzymać i wznowić przyciskiem start/stop. Po wciśnięciu stop w układzie współrzędnych pojawia się niebieski punkt. Zaznacz kilkanaście takich punktów, a następnie wybierz wykres.

Zapoznaj się z poniższym opisem symulacji, w której przedstawiono rozpad promieniotwórczy. Na podstawie opisu, wykonaj polecenie drugie.

W próbce znajduje się $1000$ jąder promieniotwórczych (szarych kółeczek). W chwili uruchomienia symulacji jądra ulegają rozpadowi, czyli przemianie promieniotwórczej (kolor kółeczka zmienia się z szarego na niebieski). Symulację można zatrzymać i wznowić przyciskiem start/stop. Po wciśnięciu stop w układzie współrzędnych pojawia się niebieski punkt. Zaznaczono kilkanaście takich punktów, a następnie wybierano wykres.

Ru55LZT7AbVEF1

Polecenie 2

R1T48OTfpYNHC

R1Xd4M88JnhO7

Jakie są podobieństwa między doświadczeniem z monetami a symulacją rozpadu promieniotwórczego?

doświadczenie z monetami	symulacja rozpadu promieniotwórczego
w kolejnych rzutach liczba orłów zmniejsza się dwukrotnie	po upływie określonego czasu liczba jąder promieniotwórczych, które nie uległy przemianie, zmniejsza się dwukrotnie
nie można przewidzieć, w którym rzucie konkretna moneta wypadnie zwrócona orłem do góry	nie można przewidzieć czasu, po którym jądro ulegnie rozpadowi
punkty otrzymane w doświadczeniu nie leżą dokładnie na krzywej	punkty otrzymane w symulacji nie leżą dokładnie na krzywej

Zarówno w przypadku rozpadu promieniotwórczego, jak i rzutu monetami, mamy do czynienia z zanikiem wykładniczym. W obu sytuacjach pomiędzy punktami w układzie współrzędnych można poprowadzić fragment wykresu funkcji, tak aby wykres tej funkcji leżał jak najbliżej każdego punktu, choć niekoniecznie punkty leżą dokładnie na krzywej. Tak dopasowany wykres funkcji z dość dobrym przybliżeniem opisuje rzeczywiste zjawisko. Skoro dopasowaliśmy krzywą do wyników doświadczenia lub symulacji, to możemy znaleźć równanie, które opisuje daną krzywą.

W przypadku rzutu monetami wzór opisujący wyniki doświadczenia ma postać:

y = k \cdot {(\frac{1}{2})}^{x}

gdzie:

$y$ – liczba wyrzuconych orłów,

$k$ – liczba monet użytych w doświadczeniu,

$x$ – kolejny numer rzutu.

Przez analogię możemy znaleźć wzór, który opisuje rozpad promieniotwórczy. Wtedy numerem rzutu $x$ będzie informacja, ile razy upłynął czas $T$ od chwili uruchomienia symulacji. Na przykład, jeżeli od początku symulacji upłynął czas $2 T$ , to $x = \frac{2 T}{T} = 2$ . Jeżeli czas jest równy $3 T$ , to $x = \frac{3 T}{T} = 3$ . Stąd wzór opisujący rozpad promieniotwórczy ma postać:

N = N_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}

gdzie:
$N$ – liczba jąder promieniotwórczych w próbce, które nie uległy rozpadowi,

$N_{0}$ – początkowa liczba jąder promieniotwórczych w próbce,

$t$ – czas, który upłynął od początku obserwacji próbki,

$T$ – czas, w którym połowa jąder promieniotwórczych uległa rozpadowi, zwany czasem połowicznego rozpadu.

Czas połowicznego rozpadu jest wielkością, która charakteryzuje izotop promieniotwórczy. Może być niezwykle krótki lub bardzo długi.

izotop	czas połowicznego rozpadu
polon- $212$	$3 \cdot 10^{- 9} s$
azot- $13$	$10$ minut
sód- $24$	$15$ godzin
jod- $131$	$8$ dni
kobalt- $60$	$5, 3$ lat
cez- $137$	$30$ lat
węgiel- $14$	$5730$ lat
jod- $129$	$1, 57 \cdot 10^{7}$ lat

Przykładowe wartości czasów połowicznego rozpadu dla wybranych izotopów. Źródło: Wikipedia

W praktyce nie posługujemy się liczbą jąder promieniotwórczych w próbce, lepiej posługiwać się masą izotopu promieniotwórczego. Liczbę jąder izotopu promieniotwórczego zastępuje masa:

m = m_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}

gdzie:
$m$ – masa izotopu promieniotwórczego w próbce, który nie uległ rozpadowi
$m_{0}$ – początkowa masa izotopu promieniotwórczych w próbce
$t$ – czas, który upłynął od początku obserwacji próbki
$T$ – czas połowicznego rozpadu

Przykład 1

Scyntygrafia jest jedną z metod diagnostycznych wykorzystywanych w medycynie nuklearnej do badania tarczycy, mózgu oraz do poszukiwania zmian nowotworowych. Na początku badania wprowadza się do organizmu pacjenta substancję, która zawiera izotop promieniotwórczy. Emitowane przez pacjenta promieniowanie jest rejestrowane przez specjalne urządzenie (detektor). Jednym z izotopów stosowanych podczas tego badania jest technet- $99 m$ . Jego czas połowicznego rozpadu to $6$ godzin.

Do organizmu pacjenta wprowadzono substancję zawierającą $2 μg$ technetu- $99 m$ . Oblicz po jakim czasie, ilość technetu- $99 m$ w organizmie zmniejszy się do:

$0, 125 μg$
$0, 1 μg$

Pytanie 1
Oblicz, po jakim czasie ilość technetu- $99 m$ w organizmie zmniejszy się do
$0, 125 μg$ .

Odpowiedź na to pytanie możemy znaleźć dwoma sposobami.

Sposób 1

R11D1pn6MrlZU

W tle prezentacji znajdują się atomy pewnego pierwiastka chemicznego.

Slajd 1. Zapisano masę początkową izotopu $m_{0}$ równą 2 mikrogramy. Masę izotopu po upływie czasu t, $m_{0}$ równą dwanaście setnych oraz czas połowicznego rozpadu T, równego 6 godzin.

Slajd 2. Początkowa masa izotopu to 2 mikrogramy.

Slajd 3. Czas połowicznego rozpadu technetu $T_{c} - 99 m$ jest równy 6 godzin. Od dwóch mikrogramów narysowano poziomą strzałkę skierowaną w prawą stronę, a nad nią zapisano czas 6 godzin.

Slajd 4. Po prawej stronie strzałki zapisano 1 mikrogram. Oznacza to, że po sześciu godzinach masa izotopu jest równa połowie, czyli jednemu mikrogramowi.

Slajd 5. Od jednego mikrograma narysowano strzałkę skierowaną do masy jednej drugiej mikrograma. Nad strzałką ponownie zapisano czas sześciu godzin. Oznacza to, że po kolejnych sześciu godzinach, masa izotopu znów zmniejsza się o połowę.

Slajd 6. Od masy jednej drugiej mikrograma narysowano strzałkę skierowaną do masy jednej czwartej mikrograma. Nad strzałką również zapisano 6 godzin. Od masy jednej czwartej mikrograma narysowano strzałkę skierowaną do masy jednej ósmej mikrograma, czyli 125 tysięcznych, nad strzałką ponownie zapisano 6 godzin. W ten sposób dochodzimy do wniosku, że izotop będzie miał masę studwudziestupięciu mikrograma po upływie dwudziestu czterech godzin.

Sposób 2

Skorzystamy ze wzoru: $m = m_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$ .

Podstawiamy wartości z treści zadania:

$0, 125 = 2 \cdot {(\frac{1}{2})}^{\frac{t}{6}}$

$\frac{0, 125}{2} = {(\frac{1}{2})}^{\frac{t}{6}}$

$\frac{1}{16} = {(\frac{1}{2})}^{\frac{t}{6}}$

${(\frac{1}{2})}^{4} = {(\frac{1}{2})}^{\frac{t}{6}}$

Z porównania wykładników otrzymujemy: $4 = \frac{t}{6}$ .

Stąd $t = 24$ godziny.

Pytanie 2
Odpowiedź w pytaniu $2$ nie jest tak oczywista, jak w pytaniu $1$ . Wiemy, że po upływie $18$ godzin (czyli trzech okresach połowicznego rozpadu) masa radioaktywnego izotopu jest równa $0, 25 μg$ , natomiast po upływie $24$ godzin (czyli czterech okresach połowicznego rozpadu) masa tego izotopu to $0, 125 μg$ . Czas, po którym masa izotopu jest równa $0, 2 μg$ , będziemy mogli obliczyć w przybliżeniu, stosując logarytmy.

Skorzystamy ze wzoru: $m = m_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$ .

Podstawiamy wartości z treści zadania:

$0, 2 = 2 \cdot {(\frac{1}{2})}^{\frac{t}{6}}$

$\frac{0, 2}{2} = {(\frac{1}{2})}^{\frac{t}{6}}$

$0, 1 = {(\frac{1}{2})}^{\frac{t}{6}}$

Skorzystamy z własności, że $\frac{1}{2} = 2^{- 1}$ .

$0, 1 = 2^{- \frac{t}{6}}$

Skoro obie strony równania są liczbami dodatnimi, to możemy zapisać:

$\log_{2} 0, 1 = \log_{2} 2^{- \frac{t}{6}}$

$\log_{2} 10^{- 1} = - \frac{t}{6}$

$- \log_{2} 10 = - \frac{t}{6}$

$t = 6 \log_{2} 10$

Do obliczenia czasu skorzystamy ze wzoru na zmianę podstawy logarytmu, a wartości logarytmów dziesiętnychlogarytm dziesiętnylogarytmów dziesiętnych odczytamy z tablic.

$t = 6 \cdot \frac{\log 10}{\log 2} = 6 \cdot \frac{1}{\log 2} \approx 6 \cdot \frac{1}{0, 3010} \approx 19, 9 \approx 20$ godzin

Pojęcia analogiczne do czasu połowicznego rozpadu można spotkać również w innych gałęziach nauki. Na przykład w farmakologii funkcjonuje czas połowicznego rozkładu leku. Okazuje się, że stężenie większości leków po ich podaniu i wchłonięciu zmniejsza się wykładniczo. Czas, w którym stężenie leku we krwi zmniejsza się o połowę wartości początkowej, nazywa się właśnie czasem połowicznego rozkładu leku lub biologicznym czasem półtrwania. W takiej sytuacji zmianę stężenia leku we krwi można opisać wzorem:

$c = c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$

gdzie:
$c$ – stężenie leku we krwi po upływie czasu $t$ od podania
$c_{0}$ – początkowe stężenie leku
$t$ – czas, który minął od chwili podania leku
$T$ – czas połowicznego rozkładu leku

substancja	biologiczny czas półtrwania
paracetamol	$2 - 4 h$
ibuprofen	$1, 8 - 4 h$
kwas acetylosalicylowy	$3 h$
morfina	$2 - 4 h$
penicylina	$0, 4 - 0, 9 h$
loratadyna	$8 h$

Źródło: Wikipedia

Wzór na zmianę stężenia leku we krwi można również zapisać w postaci:

$c = c_{0} \cdot e^{- k t}$

gdzie:
$k$ – stała szybkości rozkładu leku (jej wartość zależy od rodzaju leku i cech organizmu pacjenta).

Liczba $e$ , która pojawia się jako podstawa potęgi, jest nazywana liczbą Eulera lub liczbą Napiera. Podobnie do liczby $π$ , liczba $e$ jest niewymierna.

$e = 2, 718281828459045235360287 \dots$

Odkryto ją w $XVII$ wieku. Z czasem okazała się być jedną z podstawowych stałych przyrody – pojawia się w wielu prawach matematycznych, statystycznych, fizycznych i nie tylko.

Liczba $e$ często występuje jako podstawa potęgi, a więc w równaniach wykładniczych. W niektórych sytuacjach do rozwiązywania równań wykładniczych stosujemy logarytmy.

Na przykład: $3^{x} = 5$ .

Dobieramy wtedy logarytm o odpowiedniej podstawie:
$\log_{3} 3^{x} = \log_{3} 5$ i otrzymujemy $x = \log_{3} 5$ .

Podobnie, gdy chcemy rozwiązać równanie $e^{x} = 5$ , korzystamy z logarytmu, którego podstawą jest liczba $e$ . Zamiast jednak pisać „ $\log_{e}$ ” piszemy symbol „ $\ln$ ”, który czytamy: logarytm naturalny. Wtedy:

$e^{x} = 5$

$\ln e^{x} = \ln 5$

$x = \ln 5$

Wartość wyrażenia $\ln 5$ odczytujemy z tablic wartości logarytmów naturalnych.

Przykład 2

Uzasadnimy, że ze wzoru $c = c_{0} \cdot e^{- k t}$ wynika wzór $c = c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$ (oba wzory opisują zmianę stężenia leku we krwi z upływem czasu).

RWj79XOtXdjoP

W tle przedstawiono blistry tabletek. Zapisano wzory $c = c_{0} \cdot e^{- k t}$ oraz $c = c_{0} \cdot {(\frac{1}{2})}^{\frac{1}{T}}$ . Przeprowadzimy rozumowanie, z którego będzie wynikało, że oba wzory na zmianę stężenia leku we krwi są równoważne. W tym celu skorzystamy z definicji czasu połowicznego zaniku. Zapisujemy wzór $c = c_{0} \cdot e^{- k t}$ . Zapisano $\frac{1}{2} c = c_{0} \cdot e^{- k T}$ . Po upływie czasu połowicznego zaniku stężenie leku we krwi zmniejszy się dwukrotnie. Dzielimy obie strony równania przez początkowe stężenie leku, czyli $c_{0}$ . Otrzymujemy $\frac{1}{2} = e^{- k T}$ . Korzystamy z własności logarytmu naturalnego, aby wyznaczyć ze wzoru stałą k. Otrzymujemy. $\ln (\frac{1}{2}) = \ln (e^{- k T})$ . Przekształcamy wzór i otrzymujemy $\ln (\frac{1}{2}) = - k T$ . Mnożymy obie strony równania przez minus jeden. Otrzymujemy $- \ln (\frac{1}{2}) = k T$ . Ponownie korzystamy z własności logarytmu. Liczbę minus jeden, która znajduje się przed logarytmem naturalnym, możemy zapisać jako wykładnik potęgi o podstawie jedna druga. Czyli zapisujemy ${\ln (\frac{1}{2})}^{- 1} = k T$ . Zauważmy że ${(\frac{1}{2})}^{- 1} = 2$ . Zatem $\ln (2) = k T$ . Po podzieleniu obu stron równania przez wielkie T, otrzymujemy związek czasu połowicznego zaniku ze stałą szybkości rozkładu leku. $k = \frac{\ln (2)}{T}$ . Wyznaczony związek wstawiamy do równania na stężenie leku. Zapisujemy zatem $c = c_{0} \cdot e^{- \frac{\ln (2)}{T} \cdot t}$ . Przekształcamy wykładnik potęgi. Otrzymujemy $c_{0} \cdot e^{- \frac{t}{T} \ln (2)}$ . Następnie wyrażenie przed logarytmem naturalnym możemy zapisać jako wykładnik potęgi o podstawie dwa. Zapisujemy więc $c_{0} \cdot e^{\ln {(2)}^{- \frac{t}{T}}}$ . Zauważmy, że liczba Eulera e jest podstawą potęgi oraz podstawą logarytmu naturalnego. Skorzystamy więc z własności logarytmy. Otrzymujemy $c_{0} \cdot 2^{- \frac{t}{T}}$ . Otrzymane wyrażenie możemy inaczej zapisać za pomocą potęgi o podstawie jedna druga $c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$ .

Ciąg wszystkich przekształceń jest postaci: $c = c_{0} \cdot e^{- k t} = c_{0} \cdot e^{- \frac{\ln 2}{T} t} = c_{0} \cdot e^{- \frac{t}{T} \ln 2} = c_{0} \cdot e^{\ln 2^{- \frac{t}{T}}} = c_{0} \cdot 2^{- \frac{t}{T}} = c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$

Przykład 3

Po upływie $2, 5$ godziny stężenie leku we krwi pacjenta zmniejszyło się o $25 %$ . Oblicz okres połowicznego rozkładu tego leku.

Skorzystamy ze wzoru: $c = c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$ .

Należy go tak przekształcić, aby otrzymać okres połowicznego zaniku leku $T$ .

$c = c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}} | : c_{0}$

$\frac{c}{c_{o}} = {(\frac{1}{2})}^{\frac{t}{T}}$

$\frac{c}{c_{0}} = 2^{- \frac{t}{T}}$

Korzystamy z własności logarytmu, aby przekształcić równanie wykładnicze w równanie liniowe.

$\log_{2} \frac{c}{c_{0}} = \log_{2} 2^{- \frac{t}{T}}$

$\log_{2} \frac{c}{c_{0}} = - \frac{t}{T} \log_{2} 2$

$\log_{2} \frac{c}{c_{0}} = - \frac{t}{T}$

$\log_{2} \frac{c}{c_{0}} = - \frac{t}{T} | \cdot T$

$T \cdot \log_{2} \frac{c}{c_{0}} = - t | : \log_{2} \frac{c}{c_{0}}$

$T = \frac{- t}{\log_{2} \frac{c}{c_{0}}}$

Podstawiamy wartości z treści zadania.

$T = \frac{- 2, 5}{\log_{2} \frac{0, 75 c_{0}}{c_{0}}} = \frac{- 2, 5}{\log_{2} 0, 75}$

W tablicach logarytmów znajdziemy wartości logarytmów dziesiętnych lub naturalnych. Dlatego też, aby obliczyć wartość wyrażenia $\log_{2} 0, 75$ , skorzystamy ze wzoru na zmianę podstawy logarytmu. LogarytmlogarytmLogarytm o podstawie $2$ zamienimy na iloraz logarytmów dziesiętnych.

$T = \frac{- 2, 5}{\log_{2} 0, 75} = \frac{\frac{- 2, 5}{\log 0, 75}}{\log 2} = \frac{- 2, 5 \log 2}{\log 0, 75} = \frac{- 2, 5 \log 2}{\log (7, 5 \cdot 0, 1)} = \frac{- 2, 5 \log 2}{\log 7, 5 + \log 0, 1} \approx \frac{- 2, 5 \cdot 0, 3010}{0, 8751 - 1} \approx 6, 025$

Czas połowicznego zaniku leku to około $6$ godzin.

Przykład 4

Pacjentowi podano lek, a następnie zmierzono jego stężenie we krwi o godzinie $9 : 00$ . Na wykresie przedstawiono, w jaki sposób zmienia się stężenie tego leku we krwi. Podczas leczenia stężenie leku nie powinno być niższe od $7 \frac{μg}{ml}$ , a jego czas połowicznego rozkładu jest równy $11$ godzin. Oblicz, z dokładnością do $10$ minut, o której godzinie pacjent powinien przyjąć kolejną dawkę leku.

R1K2nWxmtxzeq

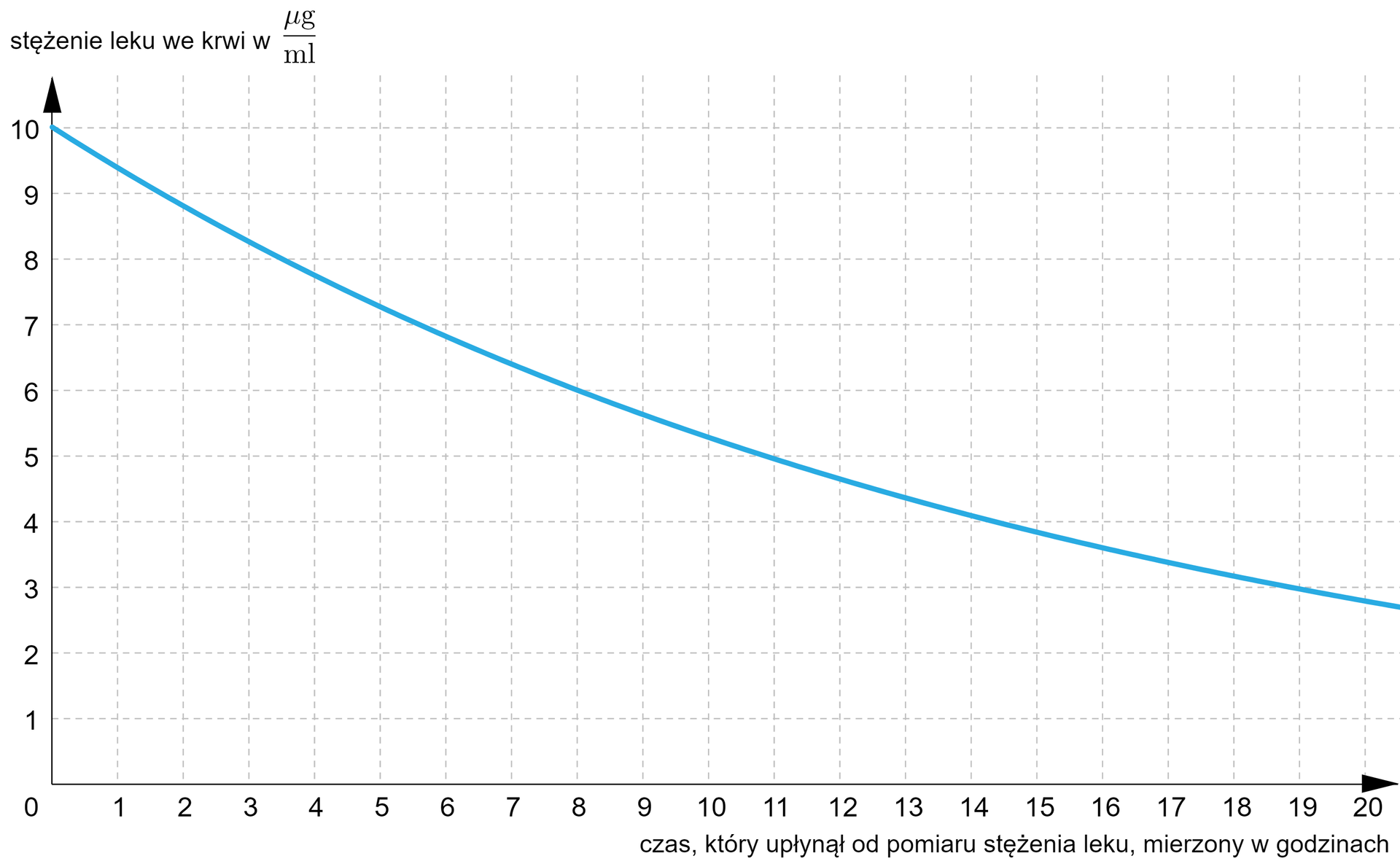
Na ilustracji przedstawiono wykres przedstawiający zależność poziomu stężenia leku we krwi od czasu, który upłynął od pomiaru stężenia. Na poziomej osi przedstawiono czas od zera do dwudziestu z podziałką co jeden, w jednostce godzin. Na pionowej osi przedstawiono poziom stężenia leku, od zera do dziesięciu z podziałką co jeden, w jednostce mikrogramów na mililitr. Wykres stanowi krzywa, malejąca, która wypłaszcza się do osi poziomej. Gdy wartość godzin na osi poziomej jest równa zero, poziom stężenia leku wynosi 6 mikrogramów na mililitr. Po ośmiu godzinach poziom stężenia to około sześć mikrogramów na mililitr. Po jedenastu godzinach to około 5 mikrogramów na mililitr.

Do rozwiązania zadania skorzystamy ze wzoru: $c = c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}}$ .

Z wykresu odczytujemy i przyjmujemy, że $10 \frac{μg}{ml}$ jest początkowym stężeniem leku we krwi pacjenta. Obliczymy czas $t$ , który upłynie do chwili, gdy stężenie leku spadnie do $7 \frac{μg}{ml}$ . W tym celu przekształcamy powyższy wzór i wyznaczamy ze wzoru czas $t$ .

$c = c_{0} \cdot {(\frac{1}{2})}^{\frac{t}{T}} | : c_{0}$

$\frac{c}{c_{0}} = {(\frac{1}{2})}^{\frac{t}{T}}$

$\frac{c}{c_{0}} = 2^{- \frac{t}{T}}$

Korzystamy z własności logarytmulogarytmlogarytmu, aby przekształcić równanie wykładnicze w równanie liniowe.

$\log_{2} \frac{c}{c_{0}} = \log_{2} 2^{- \frac{t}{T}}$

$\log_{2} \frac{c}{c_{0}} = - \frac{t}{T} \log_{2} 2$

$\log_{2} \frac{c}{c_{0}} = - \frac{t}{T}$

$\log_{2} \frac{c}{c_{0}} = - \frac{t}{T} | \cdot T$

$T \cdot \log_{2} \frac{c}{c_{0}} = - t$

$t = - T \cdot \log_{2} \frac{c}{c_{0}}$

Podstawiamy wartości z treści zadania.

$t = - 11 \cdot \log_{2} \frac{7}{10} = - 11 \cdot \log_{2} \frac{7}{10} = - 11 \cdot \frac{\log 0, 7}{\log 2} = - 11 \cdot \frac{\log 7 + \log 0, 1}{\log 2} \approx$ $\approx - 11 \cdot \frac{0, 8451 - 1}{0, 3010} \approx 5, 66$

Zatem $t \approx 5, 66$ godziny.

Obliczymy, ile minut stanowi $0, 66$ godziny.

$0, 66 \cdot 60$ minut = $39, 6$ minuty $\approx 40$ minut

Pacjent powinien otrzymać kolejną dawkę leku po upływie $5$ godzin $40$ minut od chwili pomiaru stężenia leku we krwi, czyli lekarstwo powinno zostać podane o godzinie $14 : 40$ .

Ciekawostka

Ważnym zagadnieniem związanym z lotami kosmicznymi jest ruch rakiety. W czasie lotu jej masa zmniejsza się, ponieważ paliwo zostaje spalone. Wpływa to na osiąganą przez rakietę szybkość. Związek ten opisuje wzór Ciołkowskiego:

$Δ v = v_{wzgl} \ln \frac{m_{0}}{m_{k}}$

gdzie:
$Δ v$ – wzrost szybkości rakiety
$v_{wzgl}$ – prędkość spalin względem rakiety
$m_{0}$ – masa początkowa rakiety
$m_{k}$ – masa końcowa rakiety

Słownik

logarytm

logarytmem liczby dodatniej $b$ przy podstawie $a$ dodatniej i różnej od jedności, nazywamy wykładnik potęgi, do której należy podnieść $a$ , aby otrzymać $b$

logarytm dziesiętny

logarytm o podstawie $10$

Wprowadzenie

Animacja

Słownik