Popularyzatorem łamigłówki znanej jako Wieże Hanoi jest francuski matematyk Édouard Lucas. Zajmował się on m.in. badaniem właściwości ciągu Fibonacciego (podał wzór na jego n‑ty wyraz) i opracował własną metodę sprawdzania, czy liczba naturalna jest liczbą pierwszą. Ideę Wież Hanoi Lucas przedstawił w 1883 roku.

Na czym polega zagadka Wież Hanoi?

Zagadka Wież Hanoi polega na przeniesieniu n krążków z jednego słupka na drugi. Musi jednak zostać spełnionych kilka warunków:

• krążki muszą mieć różne średnice,

• wszystkie krążki początkowo są nałożone na jeden ze słupków,

• krążki są ułożone w kolejności od krążka o największej średnicy (na dole słupka) do krążka o najmniejszej średnicy (na górze słupka),

• jednorazowo możemy przenieść tylko jeden krążek,

• nie można położyć większego krążka na mniejszym,

• mamy do dyspozycji dodatkowy, pomocniczy słupek, na który możemy tymczasowo nakładać krążki.

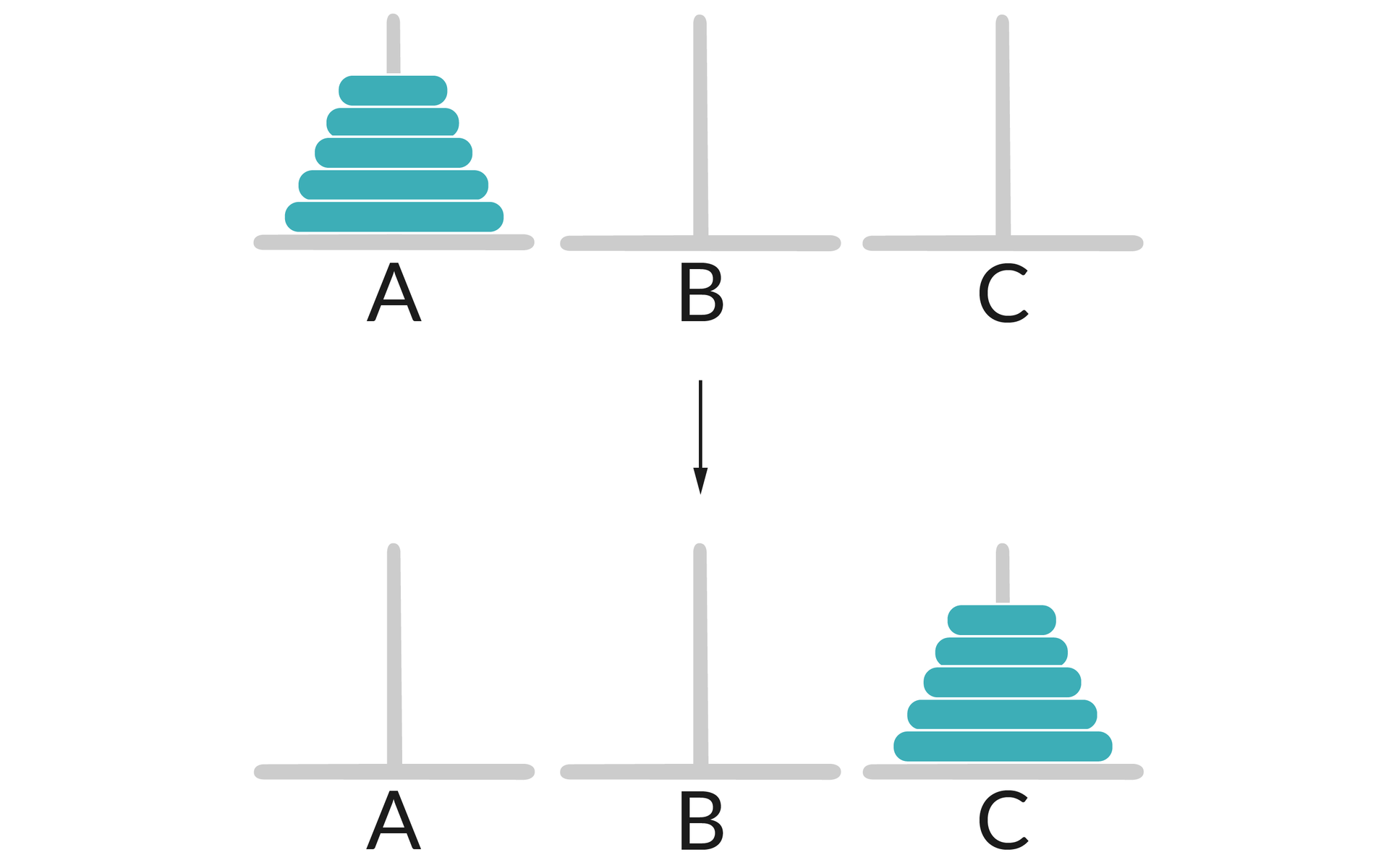
Gdy wszystkie krążki znajdą się na docelowym słupku, uznajemy problem za rozwiązany. Poniżej został zobrazowany stan początkowy – wszystkie krążki znajdują się na słupku A, a następnie stan końcowy – wszystkie krążki znajdują się na słupku C. Pomocniczym słupkiem jest słupek B.

RdHYtzjRP3egy

Zdjęcie przedstawia krążki ustawione na słupkach.
W pierwszym rzędzie znajdują się słupki podpisane jako A, B, C, a wszystkie krążki ułożone są na słupku A w kolejności od największego do najmniejszego
W drugim rzędzie krążki ustawione są w tej samej kolejności na słupku z oznaczeniem C.

Rozwiązanie iteracyjne

Zastanówmy się, w jaki sposób rozwiązać zagadkę Wież Hanoi iteracyjnieiteracjaiteracyjnie.

Aby rozwiązać problem, krążki musimy przekładać na zmianę. Pierwszym krokiem jest przeniesienie najmniejszego krążka ze słupka, na którym jest nałożony, na kolejny słupek. Kolejny słupek wyznaczamy w następujący sposób:

• Jeżeli liczba krążków jest parzysta, kolejnym słupkiem jest słupek po prawej stronie, czyli ze słupka A przenosimy na słupek B, ze słupka C na słupek A.

• Jeżeli liczba krążków jest nieparzysta, kolejnym słupkiem jest ten po lewej stronie, czyli ze słupka A przenosimy na słupek C itd.

Drugi krok polega na tym, że innym krążkiem wykonamy jedyny dostępny ruch, to znaczy taki, w którym nie położymy większego krążka na mniejszy.

Dwa powyższe kroki powtarzamy tak długo, aż wszystkie krążki znajdą się na słupku C.

Kolejne etapy rozwiązania zagadki Wież Hanoi dla trzech krążków zostały przedstawione poniżej. Na czerwono zostały oznaczone krążki, które będziemy przenosić, natomiast na fioletowo krążki, które zostały właśnie przeniesione.

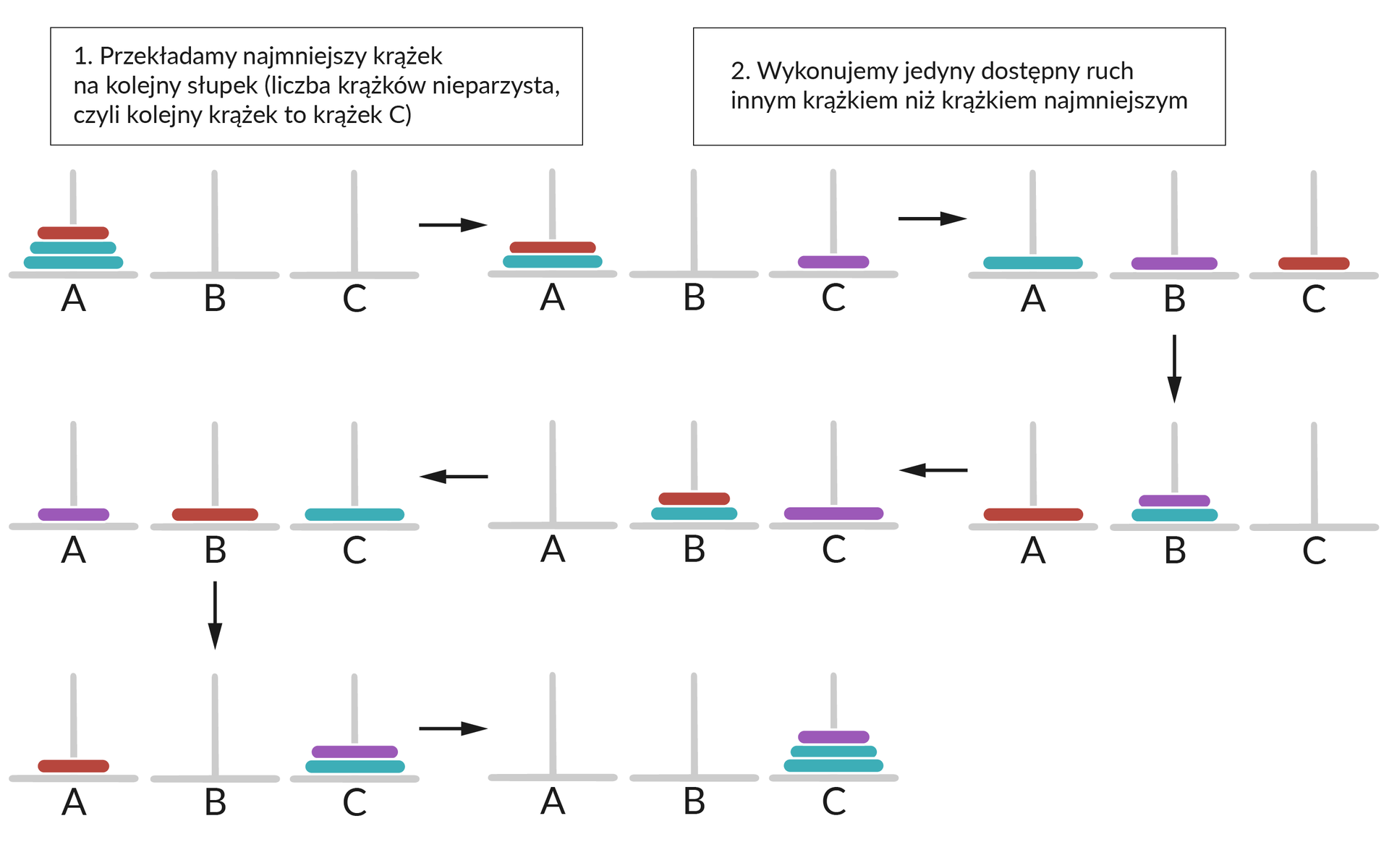
Jak widać na powyższym obrazku, wykonaliśmy siedem ruchów w celu przeniesienia trzech krążków.

Buddyjska legenda a informatyka

Dlaczego na lekcji informatyki w ogóle zajmujemy się układanką pochodzącą z czasów, gdy nie istniały jeszcze komputery? Otóż Wieże Hanoi zbudowane są podobnie do struktury danych zwanej stosemstosstosem, wykorzystywanej przez procesory podczas przetwarzania informacji.

Tak jak w przypadku krążków składających się na wieżę, w stosie dostępny jest tylko element znajdujący się na samym jego szczycie. Jedyną różnicą jest to, że elementy stosu mają postać ciągów zer i jedynek, a nie krążków. Procesory albo odkładają dane na szczyt stosu, albo pobierają ze stosu odłożone tam elementy.

Rozwiązanie rekurencyjne

Zapisany za pomocą pseudokodu algorytm wykorzystujący rekurencjęRekurencjarekurencję wygląda w następujący sposób:

funkcja wiezaHanoi(n, A, B, C)
	jeżeli n > 0 wykonaj:
		wiezaHanoi(n - 1, A, C, B)
		wypisz: "Przeniesienie z" A "do" C
		wiezaHanoi(n - 1, B, A, C)

Rekurencyjne rozwiązanie zagadki Wież Hanoi zawarte jest w trzech krokach:

1. W trzeciej linii pseudokodu wywołujemy rekurencyjnie funkcję wiezaHanoi. Ta wywołana rekurencyjnie funkcja zrealizuje nam przeniesienie n - 1 górnych krążków ze słupka A na słupek B. Na słupku A pozostanie n-ty, największy krążek. Reszta krążków będzie nałożona na słupku B.

2. W czwartej linii przenosimy n-ty krążek ze słupka A na słupek docelowy C.

3. W piątej linii ponownie wywołujemy rekurencyjnie funkcję wiezaHanoi, aby przenieść n - 1 krążków ze słupka B na słupek C, na którym położony jest już największy krążek.

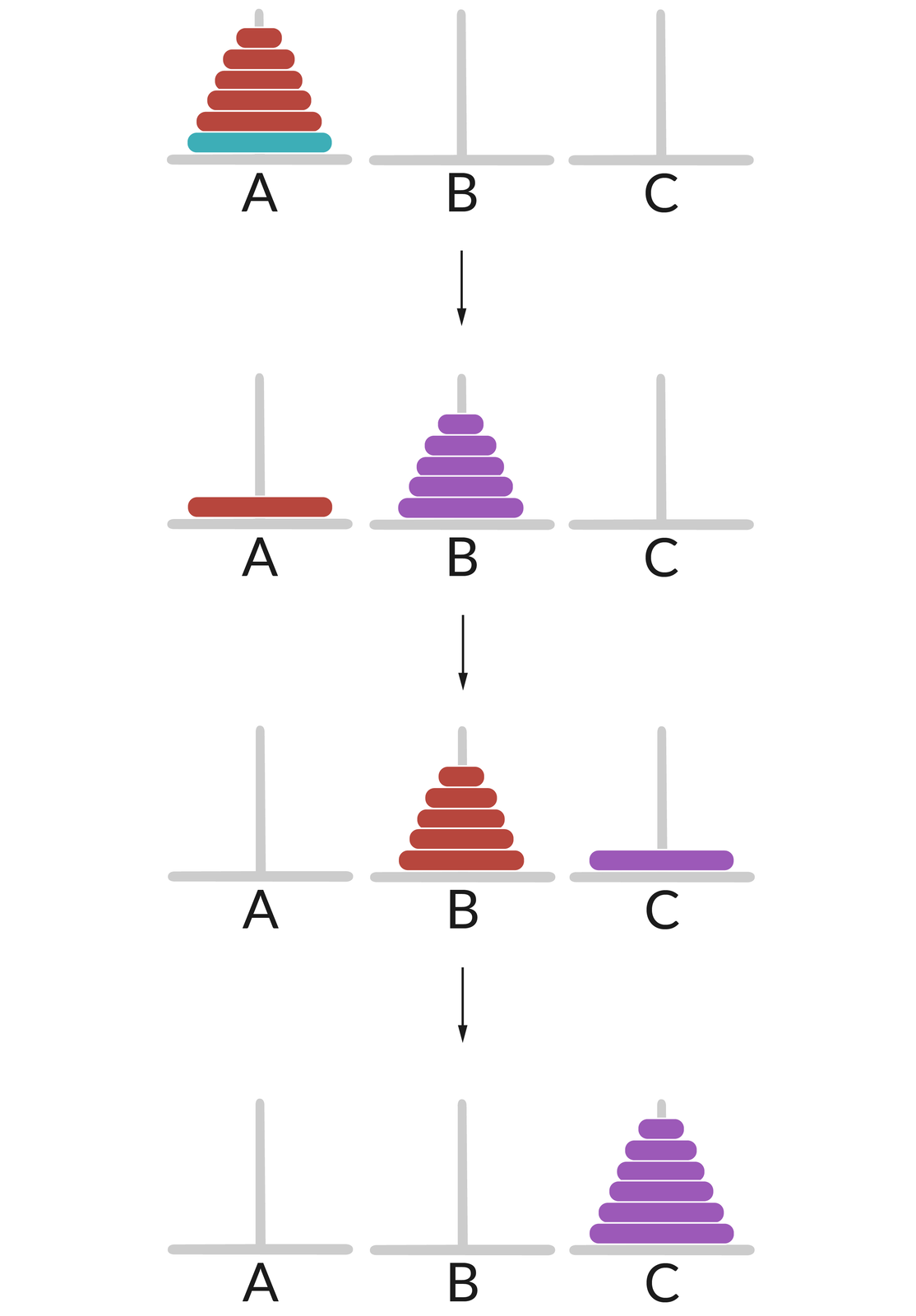
Ilustracja przedstawia kroki algorytmu rekurencyjnego dla sześciu krążków.

R1F5fvIlkOg35

Ilustracja przedstawia cztery rzędy słupków.
W każdym rzędzie znajdują się trzy słupki o oznaczeniach A, B, C.
1. Wszystkie krążki znajdują się na słupku A, w kolejności od najmniejszego do największego.
2. Krążek największy znajduje się na słupku A, reszta krążków znajduje się na słupku B w kolejności od najmniejszego do największego.
3. Krążek największy znajduje się na słupku C, reszta krążków znajduje się na słupku B w kolejności od najmniejszego do największego.
4. Wszystkie krążki znajdują się na słupku C w kolejności od najmniejszego do największego.

Złożoność obliczeniowa

Liczba przeniesień pojedynczego krążka, które należy wykonać, aby rozwiązać zagadkę Wież Hanoi wynosi:

Na przykład dla trzech krążków liczba przeniesień wynosi:

Zatem złożoność obliczeniowa algorytmu rozwiązania problemu Wież Hanoi to:

Jest to złożoność wykładniczazłożoność wykładniczazłożoność wykładnicza, to znaczy rośnie bardzo szybko wraz ze wzrostem liczby krążków, czyli parametru wejściowego.

Słownik