Przeczytaj
Przypomnijmy podstawowe wzory dotyczące walca o promieniu podstawy oraz wysokości :
objętość:
pole powierzchni:
Podgrzewacz do kominków ma kształt walcawalca o średnicy podstawy i wysokości . Ile takich podgrzewaczy możemy wykonać z wosku?
Rozwiązanie:
Obliczymy objętość jednego podgrzewacza.
Mamy więc . Ponadto mamy , czyli wosku wystarczy na wykonanie podgrzewaczy.
Szklarnia ma kształt jak na rysunku i powstała z połączenia prostopadłościanu o wymiarach i połowy walca o promieniu . Jaką powierzchnię ma poliwęglan pokrywający tę szklarnię? Wynik przybliż do . Przyjmij .
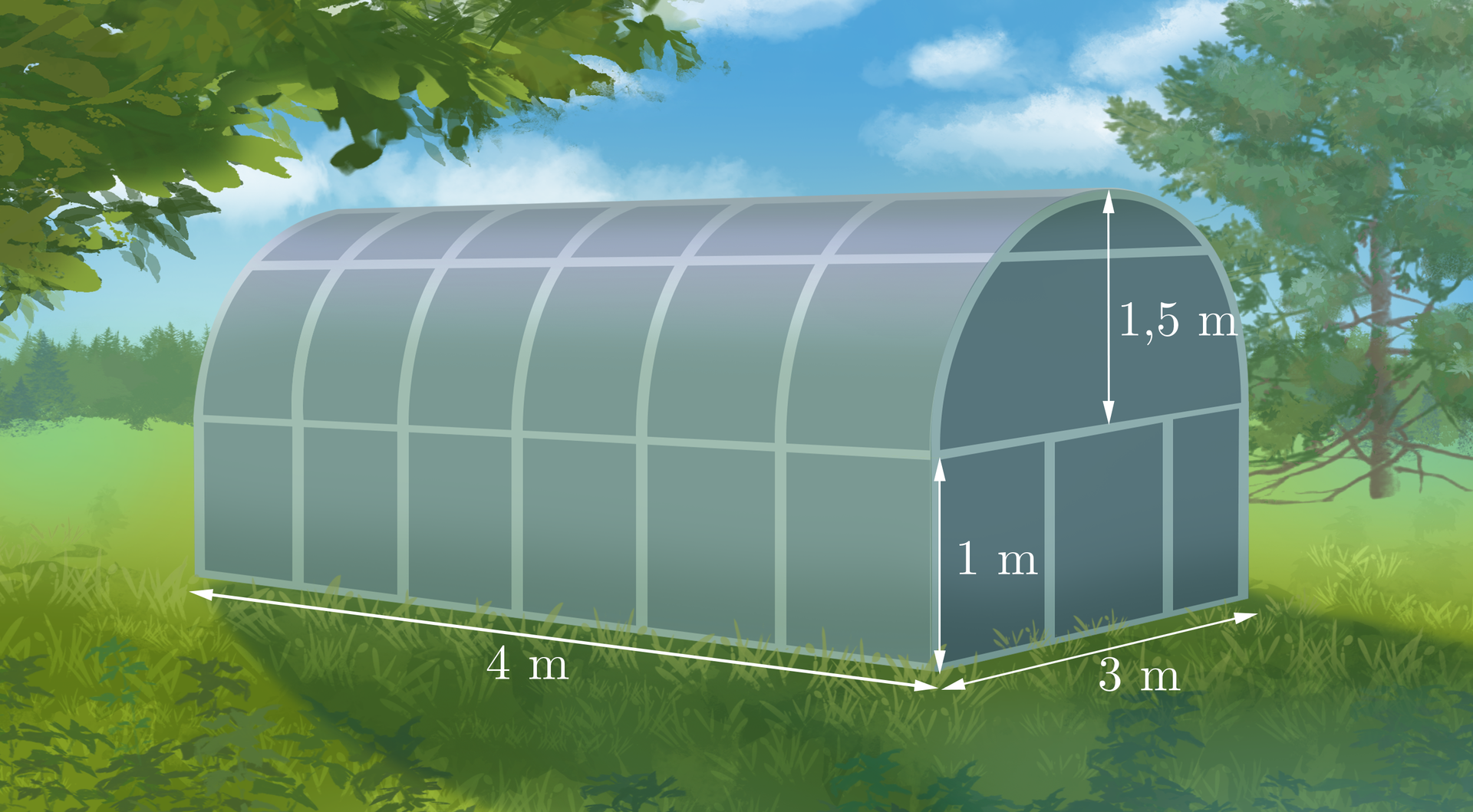
Rozwiązanie:
Obliczymy połowę powierzchni walca .
Następnie obliczamy pole powierzchni bocznej prostopadłościanu: .
A zatem poliwęglan pokrywający tę szklarnię ma powierzchnię .
W zadaniach praktycznych możemy również obliczać długości odcinków w walcu.
Do garnka o średnicy podstawy i wysokości wlano wodę wypełniając go w objętości i zaczęto gotować wodę na makaron. Po minutach wody wyparowało, a wodę przelano do garnka o średnicy . Jak wysoko sięga woda w drugim garnku? Wynik przybliż do .
Rozwiązanie:
Obliczmy objętość wody na początku gotowania: .
Po minutach mamy więc wody.
Obliczymy do jakiej wysokości będzie sięgać woda w drugim garnku:
A stąd .
Rynnę, jak na rysunku, wykonano z kawałka blachy o wymiarach . Jaka w przybliżeniu do jest średnica tej rynny? Zagięcia pomijamy. Przyjmujemy .
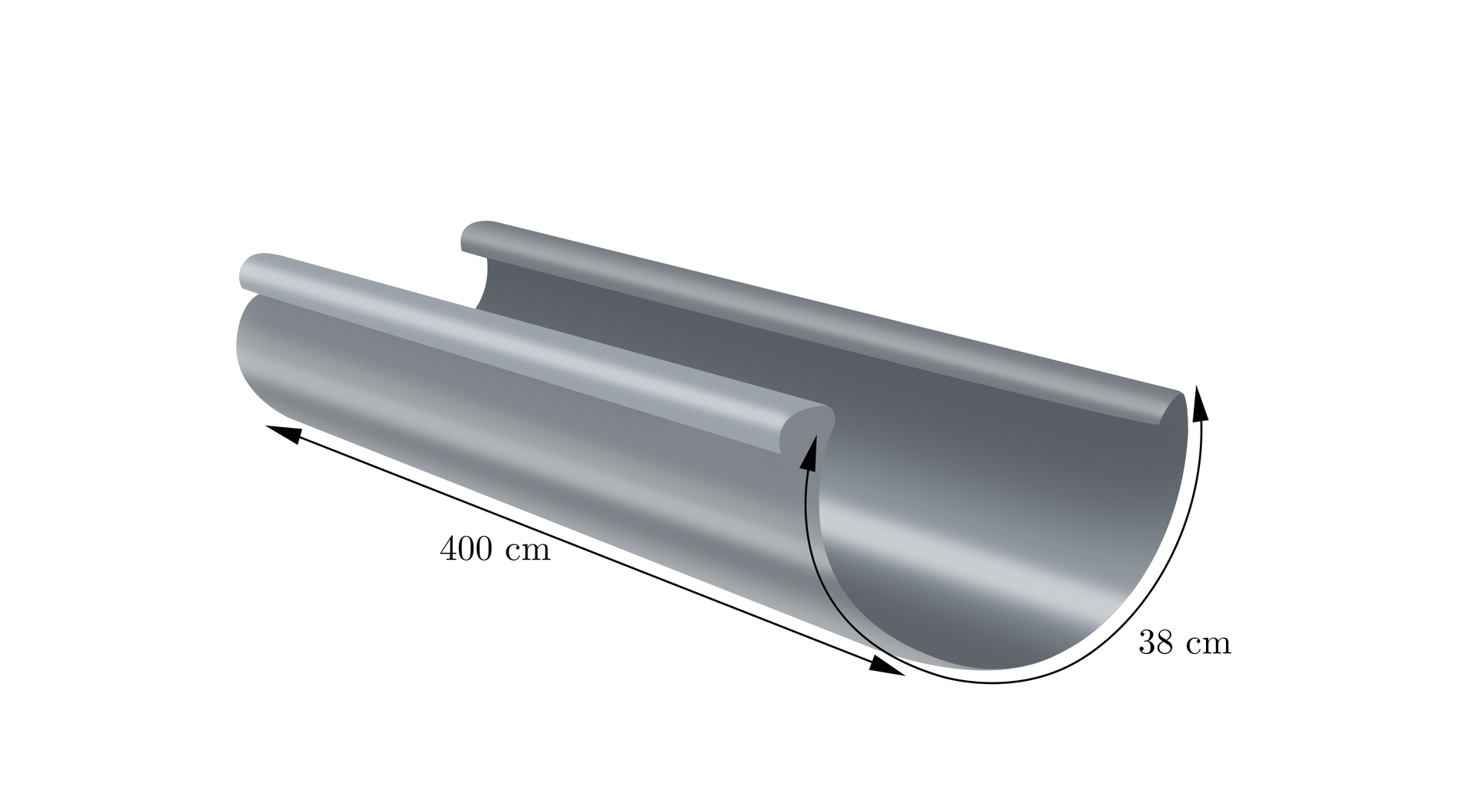
Rozwiązanie:
Połowa obwodu podstawy ma . A zatem , co po podstawieniu przybliżenia daje nam . A zatem średnica wynosi .
Przypomnijmy, że przekrój osiowy walcaprzekrój osiowy walca jest prostokątem o wymiarach .
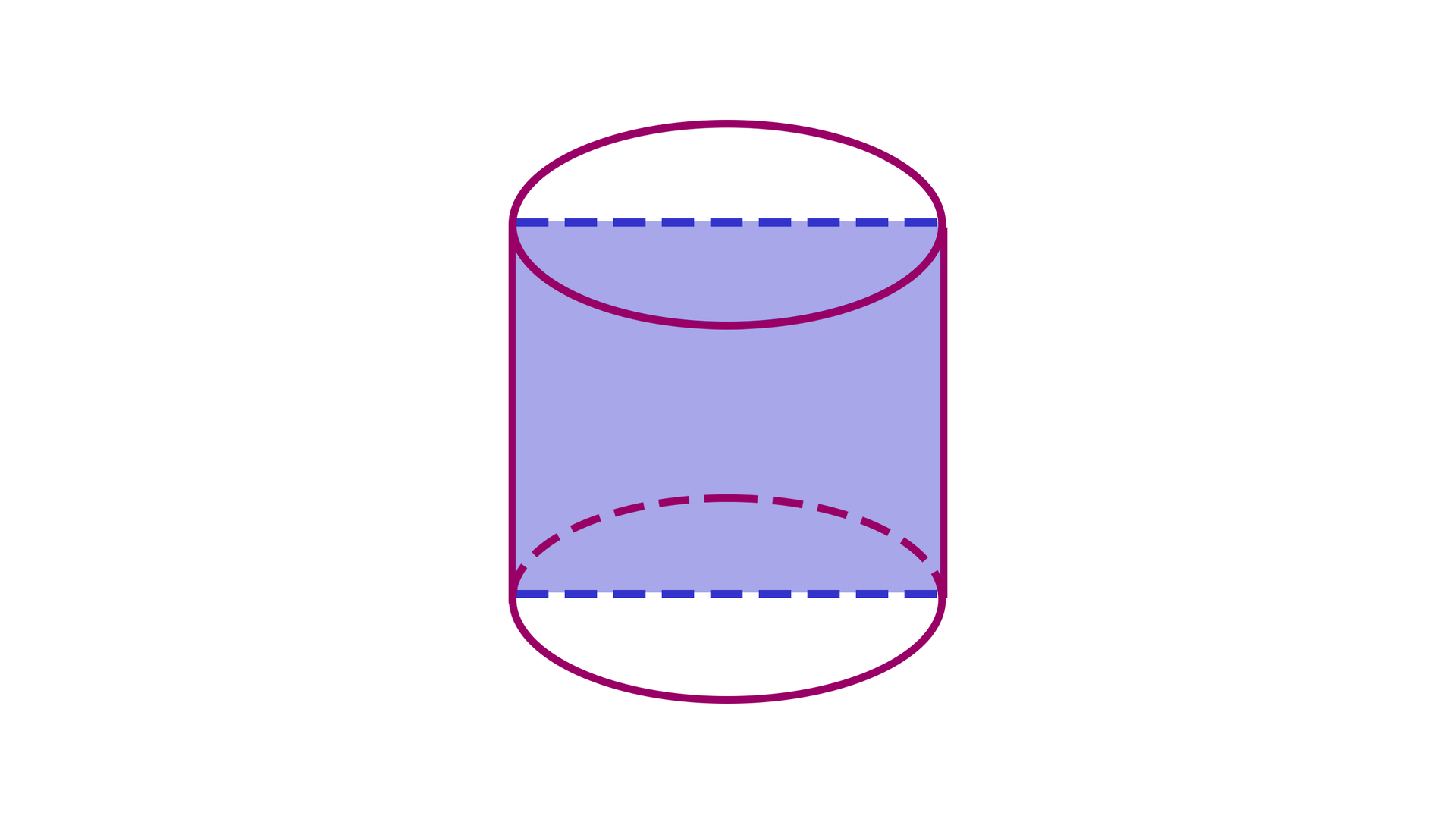
Każdy przekrój walca płaszczyzną prostopadłą do podstawy ma kształt prostokąta.
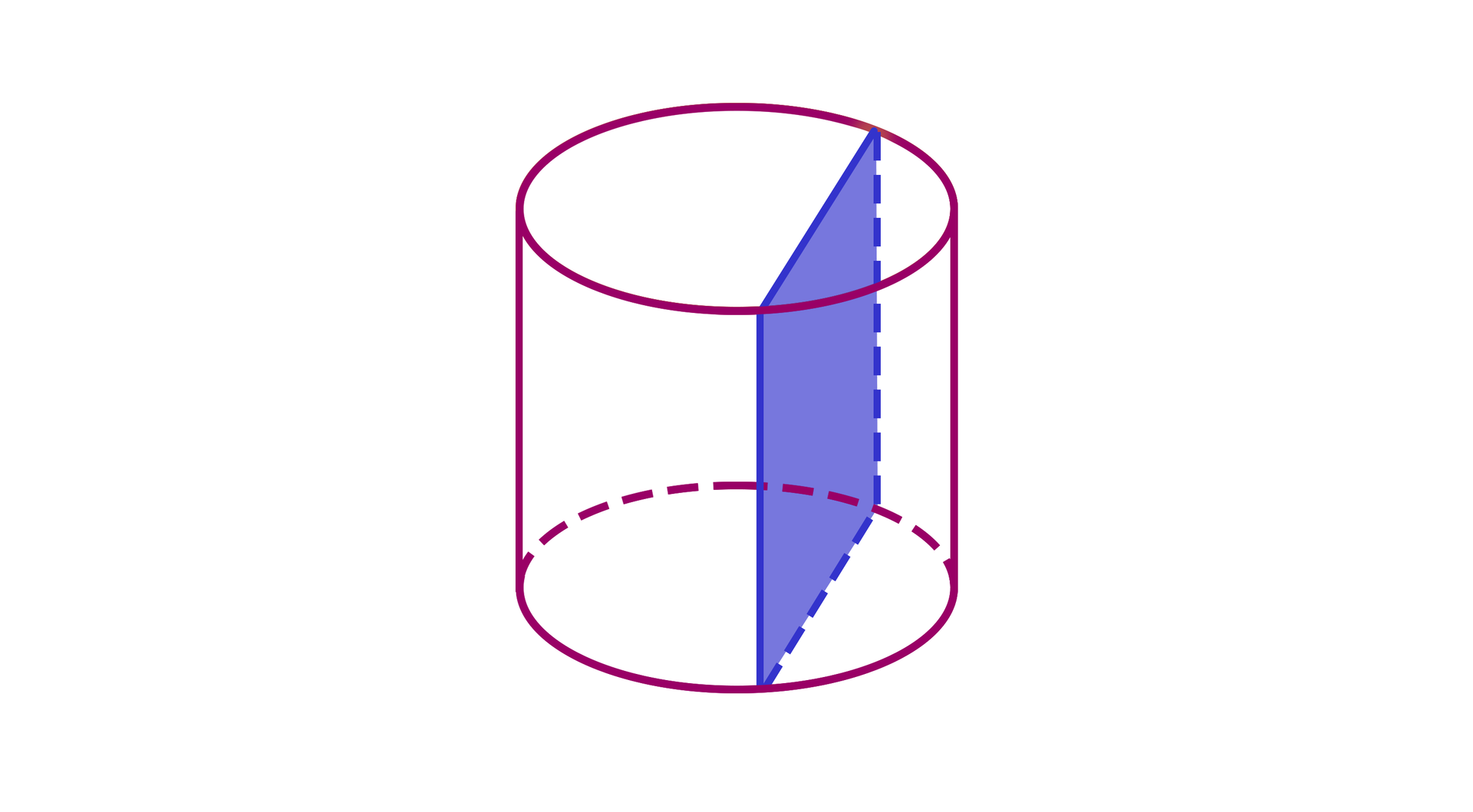
Drewniane klocki w kształcie walca o promieniu podstawy i wysokości przecięto w odległości od środka przekrojem prostopadłym do podstawy. Powstałe w ten sposób klocki pomalowano farbą akrylową o wydajności . Ile klocków możemy rozciąć i pomalować w ten sposób, jeżeli mamy do dyspozycji opakowanie o pojemności ?
Rozwiązanie:
Farbą o takiej objętości możemy pomalować .
Zróbmy rysunek pomocniczy:
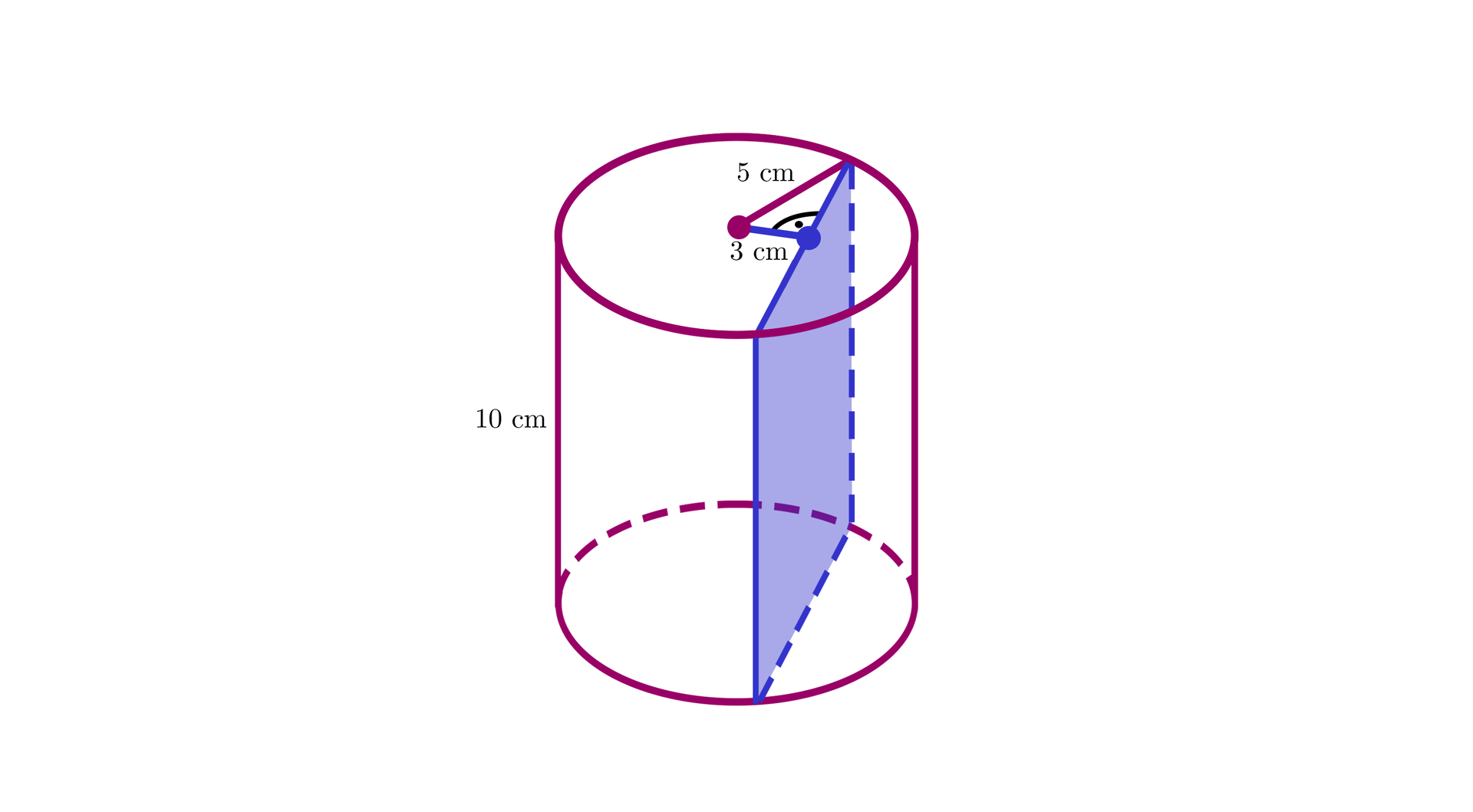
Mamy tu trójkąt Pitagorejski , , . A zatem przekrój jest prostokątem o wymiarach . Do pomalowania mamy więc powierzchnię walca i dwa pola przekroju.
A zatem .
Stąd otrzymujemy .
Czyli możemy przeciąć klocków w kształcie walca o podanych wymiarach.
Słownik
bryła obrotowa powstała przez obrót prostokąta wokół jednego z boków
przekrój walca płaszczyzną zawierającą oś obrotu walca